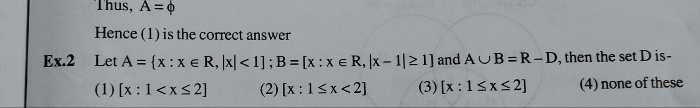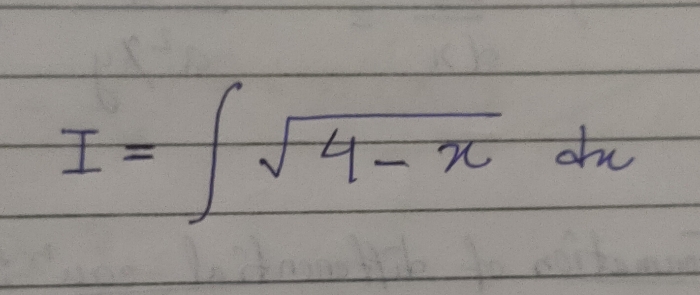Doubts and Solutions
OR
CBSE VIII - Maths
Asked by biswajitpatel88 | 10 May, 2024, 01:54: PM
CBSE VII - Maths
Asked by shaikajeema999 | 10 May, 2024, 01:13: PM
JEE Main - Maths
Asked by pandu.munganda | 10 May, 2024, 11:00: AM
CBSE VIII - Maths
Asked by biswajitpatel88 | 10 May, 2024, 10:49: AM
CBSE VIII - Maths
Asked by biswajitpatel88 | 10 May, 2024, 10:49: AM
JEE Main - Maths
Asked by prasannajitdey.babai | 10 May, 2024, 10:35: AM
CBSE XI Science - Chemistry
Asked by r84314179 | 10 May, 2024, 09:04: AM
NEET NEET - Biology
Asked by waghmarerahul43151 | 10 May, 2024, 08:44: AM