Class 11-commerce TR JAIN AND VK OHRI Solutions Statistics for Economics Chapter 10: Measures of Central Tendency- Median and Mode
Measures of Central Tendency- Median and Mode Exercise 237
Solution SAQ 1
Arranging data in ascending order:
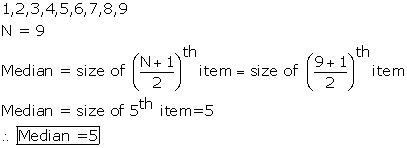
Solution SAQ 2
Arranging data in ascending order:

Solution SAQ 3

Median value corresponds to the 37th item in the series. Thus, median value is 6 as it corresponds to cumulative frequency 40.
Solution SAQ 4

Solution SAQ 5
Arranging data in the ascending order:
|
S. No |
Ages |
|
1 |
2 |
|
2 |
9 |
|
3 |
10 |
|
4 |
11 |
|
5 |
13 |
|
6 |
14 |
|
7 |
16 |
|
8 |
18 |
N = 8
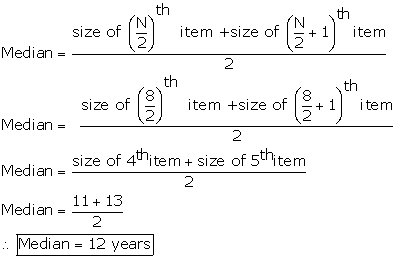
Solution SAQ 6
|
No. of person in a House |
No. of House (f) |
Cumulative Frequency (c.f.) |
|
1 |
26 |
26 |
|
2 |
113 |
139 |
|
3 |
120 |
259 |
|
4 |
95 |
354 |
|
5 |
60 |
414 |
|
6 |
42 |
456 |
|
7 |
21 |
477 |
|
8 |
14 |
491 |
|
9 |
5 |
496 |
|
10 |
4 |
500 |
|
|
∑f =500 |
|
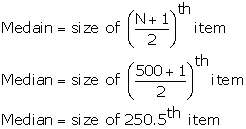
Median value corresponds to the 250.5th item in the series. Thus, median value is 3 as it corresponds to cumulative frequency 259.
Solution SAQ 7
|
Size |
Frequency (f) |
Cumulative Frequency (c.f.) |
|
15 |
10 |
10 |
|
20 |
15 |
25 |
|
25 |
25 |
50 |
|
30 |
5 |
55 |
|
35 |
5 |
60 |
|
40 |
20 |
80 |
|
|
N = 80 |
|
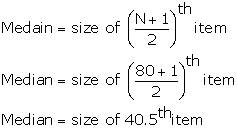
Median value corresponds to the 40.5th item in the series. Thus, median value is 25 as it corresponds to cumulative frequency 50.
Solution SAQ 8
|
Marks |
No. of Student (f) |
Cumulative Frequency (c.f.) |
|
0 |
4 |
4 |
|
5 |
6 |
10 |
|
10 |
15 |
25 |
|
15 |
5 |
30 |
|
20 |
8 |
38 |
|
25 |
12 |
50 |
|
30 |
28 |
78 |
|
35 |
14 |
92 |
|
40 |
3 |
95 |
|
45 |
5 |
100 |
|
|
N = 100 |
|
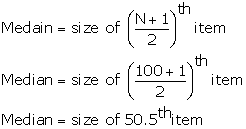
Median value corresponds to the 50.5th item in the series. Thus, median value is 30 as it corresponds to cumulative frequency 78.
Solution SAQ 9

Solution SAQ 10
Arranging the data in ascending order:

Measures of Central Tendency- Median and Mode Exercise 238
Solution SAQ 11

Solution SAQ 12

Solution SAQ 13

Solution SAQ 14

Solution SAQ 15
Lower limits and upper limits of class intervals are calculated using the following formula.
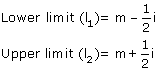
where m is mid value and i is the difference between mid-values.

Solution SAQ 16
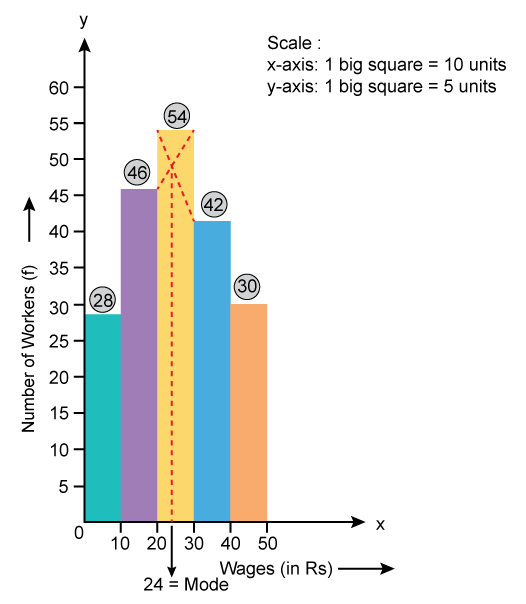

Solution SAQ 17
Mode of the given series is 75 as it has the highest frequency of 9.
Solution SAQ 18

Solution SAQ 19

Analysis Table
|
Column |
Size of items containing maximum frequency |
|||||||||
|
|
40 |
44 |
48 |
52 |
56 |
60 |
64 |
68 |
72 |
76 |
|
I |
|
|
|
✓ |
|
✓ |
|
|
|
|
|
II |
|
|
|
|
✓ |
✓ |
|
|
|
|
|
III |
|
|
|
|
|
✓ |
✓ |
|
|
|
|
IV |
|
|
|
✓ |
✓ |
✓ |
|
|
|
|
|
V |
|
|
|
|
✓ |
✓ |
✓ |
|
|
|
|
VI |
|
|
✓ |
✓ |
✓ |
|
|
|
|
|
|
Total |
- |
- |
1 |
3 |
4 |
5 |
2 |
- |
- |
- |
Mode is 60 as it repeats itself maximum number of times.
Measures of Central Tendency- Median and Mode Exercise 239
Solution SAQ 20
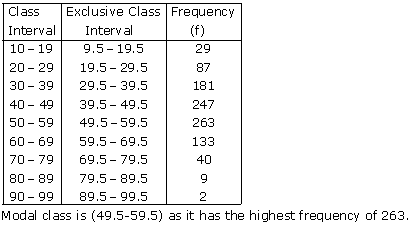
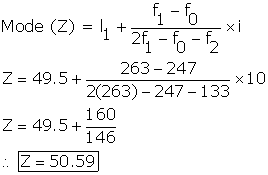
Solution SAQ 21

Solution SAQ 22
|
Wages |
No. of Wages |
|
0 - 10 |
15 |
|
10 - 20 |
35 - 15 =20 |
|
20 - 30 |
60 - 35 =25 |
|
30 - 40 |
84 - 60 =24 |
|
40 - 50 |
97 - 84 =12 |
|
50 - 60 |
127- 96 = 31 |
|
60 - 70 |
198 - 127= 71 |
|
70 - 80 |
250 - 198 = 52 |
By inspection, we can say that the modal class is 60 - 70 as it has the highest frequency of 71.

Solution SAQ 23
Mode of the given series is 5 as it has the highest frequency of 20 times.
Solution SAQ 24
|
No. of person per House (X) |
No. of House (f) |
fx |
Cumulative Frequency (c.f.) |
|
1 |
26 |
26 |
26 |
|
2 |
113 |
226 |
139 |
|
3 |
120 |
360 |
259 |
|
4 |
95 |
380 |
354 |
|
5 |
60 |
300 |
414 |
|
6 |
42 |
252 |
456 |
|
7 |
21 |
147 |
477 |
|
8 |
14 |
112 |
491 |
|
9 |
5 |
45 |
496 |
|
10 |
4 |
40 |
500 |
|
|
N=∑f = 500 |
∑fx = 1888 |
|

Solution SAQ 25
|
Marks |
No. of Workers (f) |
Cumulative Frequency (c.f.) |
|
0 - 10 |
2 |
2 |
|
10 - 20 |
18 |
20 |
|
20 - 30 |
30 |
50 |
|
30 - 40 |
45 |
95 |
|
40 - 50 |
35 |
130 |
|
50 - 60 |
20 |
150 |
|
60 - 70 |
6 |
156 |
|
70 - 80 |
3 |
159 |
|
|
N = ∑f = 159 |
|

Solution SAQ 26
|
Age |
No. of Student (f) |
Cumulative Frequency (c.f) |
|
20 - 25 |
50 |
50 |
|
25 - 30 |
70 |
120 |
|
30 - 35 |
100 |
220 |
|
35 - 40 |
180 |
400 |
|
40 - 45 |
150 |
550 |
|
45 - 50 |
120 |
670 |
|
50 - 55 |
70 |
740 |
|
55 - 60 |
60 |
800 |
|
|
∑f = 800 |
|

Solution SAQ 27
|
Marks |
Mid Value (m) |
No. of Workers (f) |
Cumulative Frequency (c.f.) |
fm |
|
0 - 10 |
5 |
5 |
5 |
25 |
|
10 - 20 |
15 |
7 |
12 |
105 |
|
20 - 30 |
25 |
15 |
27 |
375 |
|
30 - 40 |
35 |
25 |
52 |
875 |
|
40 - 50 |
45 |
20 |
72 |
900 |
|
50 - 60 |
55 |
15 |
87 |
825 |
|
60 - 70 |
65 |
8 |
95 |
520 |
|
70 - 80 |
75 |
5 |
100 |
375 |
|
|
|
N = ∑f =100 |
|
∑fm = 4000 |

Solution SAQ 28
Given:
Mode = 83
Mean = 92
Median =?
We know:
Mode = 3(Median) - 2(Mean)
83 = 3 (Median) - 2(92)
3 (Median) = 83 + 184
![]()
Measures of Central Tendency- Median and Mode Exercise 240
Solution SAQ 29
Given:
Mean = 146
Median = 130
Mode =?
Mode = 3(Median) - 2(Mean)
Mode = 3(130) - 2(146)
Mode = 390 - 292
![]()
Solution SAQ 30
Given:
Mode = 63
Median = 77
Mean =?
We know:
Mode = 3(Median) - 2(Mean)
63 = 3 (77) - 2 (Mean)
2 (Mean) = 231 - 63
![]()
Solution SAQ 31
|
Marks |
Mid Point (m) |
Cumulative Frequency |
Frequency |
fm |
|
0 - 10 |
5 |
12 |
12 |
60 |
|
10 - 20 |
15 |
26 |
14 |
210 |
|
20 - 30 |
25 |
40 |
14 |
350 |
|
30 - 40 |
35 |
58 |
18 |
630 |
|
40 - 50 |
45 |
80 |
22 |
990 |
|
50 - 60 |
55 |
110 |
30 |
1650 |
|
60 - 70 |
65 |
138 |
28 |
1820 |
|
70 - 80 |
75 |
150 |
12 |
900 |
|
|
|
|
∑f = 150 |
∑fm = 6610 |

