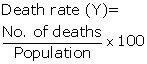Class 11-commerce TR JAIN AND VK OHRI Solutions Statistics for Economics Chapter 12: Correlation
Correlation Exercise 332
Solution SAQ 1
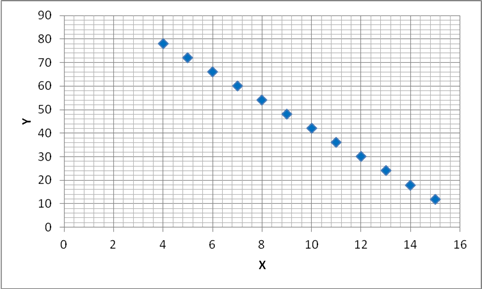
X and Y series show a perfect negative relationship between each other.
Solution SAQ 2
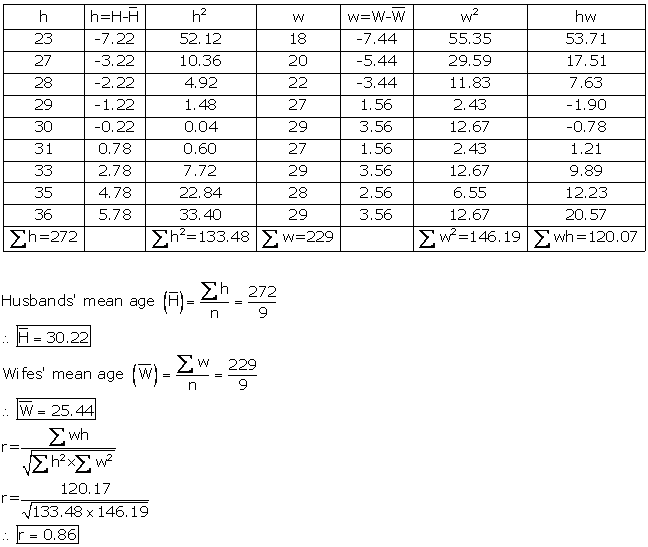
Solution SAQ 3
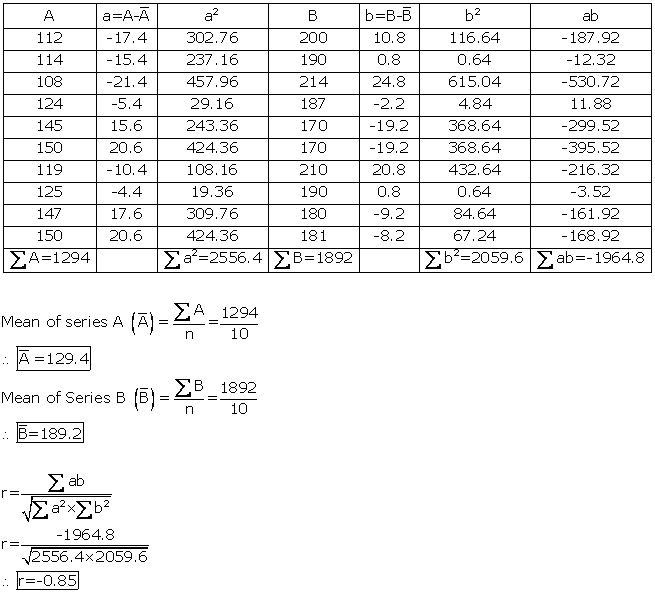
Solution SAQ 4
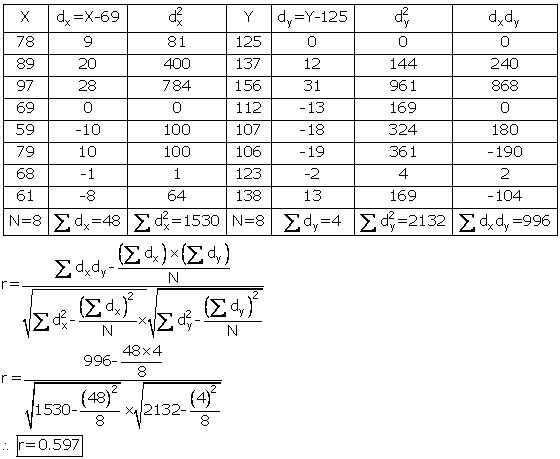
Solution SAQ 5

Solution SAQ 6
|
Economics (E) |
Rank R1 |
History (H) |
Rank R2 |
D= R1 - R2 |
D2 |
|
66 |
3 |
58 |
3.5 |
-5 |
0.25 |
|
90 |
1 |
76 |
1 |
0 |
0 |
|
89 |
2 |
65 |
2 |
0 |
0 |
|
55 |
5 |
58 |
3.5 |
1.5 |
2.25 |
|
58 |
4 |
53 |
6 |
-2 |
4 |
|
44 |
6 |
49 |
7 |
-1 |
1 |
|
42 |
7 |
56 |
5 |
2 |
4 |
|
N = 7 |
|
|
|
|
𝛴 D2 = 11.50 |
58 is repeated two times in series 2. Thus, m1= 2 and following formula is used to calculate correlation.

Solution SAQ 7
|
X |
R1 |
Y |
R2 |
D = R1 - R2 |
D2 |
|
80 |
1 |
12 |
8 |
-7 |
49 |
|
78 |
2 |
13 |
7 |
-5 |
25 |
|
75 |
3.5 |
14 |
5 |
-1.5 |
2.25 |
|
75 |
3.5 |
14 |
5 |
-1.5 |
2.25 |
|
58 |
8 |
14 |
5 |
3 |
9 |
|
67 |
5 |
16 |
2 |
3 |
9 |
|
60 |
6 |
15 |
3 |
3 |
9 |
|
59 |
7 |
17 |
1 |
6 |
36 |
|
N = 8 |
|
|
|
|
𝛴 D2 = 141.5 |
75 is repeated two times in series 1 and 14 is repeated three times in series 2. Thus, m1= 2 and m2= 3 and following formula is used to calculate correlation.

Solution SAQ 8
Karl Pearson's Method:
|
Economics (X) |
dx = X - 35 |
dx2 |
History (Y) |
dy = Y - 50 |
dy2 |
dxdy |
|
77 |
42 |
1764 |
35 |
-15 |
225 |
-630 |
|
54 |
19 |
361 |
58 |
8 |
64 |
152 |
|
27 |
-8 |
64 |
60 |
10 |
100 |
-80 |
|
52 |
17 |
289 |
46 |
-4 |
16 |
-68 |
|
14 |
-21 |
441 |
50 |
0 |
0 |
0 |
|
35 |
0 |
0 |
40 |
-10 |
100 |
0 |
|
90 |
55 |
3025 |
35 |
-15 |
225 |
-825 |
|
25 |
-10 |
100 |
56 |
6 |
36 |
-60 |
|
56 |
21 |
441 |
44 |
-6 |
36 |
-126 |
|
60 |
25 |
625 |
42 |
-8 |
64 |
-200 |
|
N = 10 |
𝛴 dx = 140 |
𝛴dx2 = 7110 |
N = 10 |
𝛴dy = -34 |
𝛴dy2 = 860 |
𝛴dxdy=-1837 |
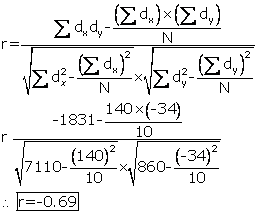
Rank Difference Method:
|
Economics |
R1 |
History |
R2 |
D = R1 - R2 |
D2 |
|
77 |
2 |
35 |
9.5 |
-7.5 |
56.25 |
|
54 |
5 |
58 |
2 |
3 |
9 |
|
27 |
8 |
60 |
1 |
7 |
49 |
|
52 |
6 |
46 |
5 |
1 |
1 |
|
14 |
10 |
50 |
4 |
6 |
36 |
|
35 |
7 |
40 |
8 |
-1 |
1 |
|
90 |
1 |
35 |
9.5 |
-8.5 |
72.25 |
|
25 |
9 |
56 |
3 |
6 |
36 |
|
56 |
4 |
44 |
6 |
-2 |
4 |
|
60 |
3 |
42 |
7 |
-4 |
16 |
|
N = 10 |
|
|
|
|
𝛴D2 = 280.5 |
35 is repeated two times in series 2. Thus, m1= 2 and following formula is used to calculate correlation.

Correlation Exercise 333
Solution SAQ 9
|
Teaching Method |
Rank of A RA |
Rank of B RB |
D = RA - RB |
D2 |
|
I |
2 |
1 |
1 |
1 |
|
II |
1 |
3 |
-2 |
4 |
|
III |
5 |
2 |
3 |
9 |
|
IV |
3 |
4 |
-1 |
1 |
|
V |
4 |
7 |
-3 |
9 |
|
VI |
7 |
5 |
2 |
4 |
|
VII |
6 |
6 |
0 |
0 |
|
N=7 |
|
|
|
𝛴D2 = 28 |

Solution SAQ 10
Examples of perfect correlation:
- Relationship between study hours and marks
- Relationship between consumption and saving from fixed income
- Relationship between amount of loan taken from bank and interest paid
|
X |
R1 |
Y |
R2 |
D=R1- R2 |
D2 |
|
48 |
3 |
13 |
5.5 |
-2.5 |
6.25 |
|
33 |
5 |
13 |
5.5 |
-0.5 |
0.25 |
|
40 |
4 |
22 |
1 |
3 |
9 |
|
9 |
9 |
6 |
8.5 |
0.5 |
0.25 |
|
16 |
7 |
14 |
4 |
3 |
9 |
|
65 |
1 |
20 |
2 |
-1 |
1 |
|
26 |
6 |
9 |
7 |
-1 |
1 |
|
15 |
8 |
6 |
8.5 |
-0.5 |
0.25 |
|
57 |
2 |
15 |
3 |
0.1 |
1 |
|
N = 9 |
|
|
|
|
𝛴 D2 = 28 |
13 and 6 are repeated two times in series 2. Thus, m1= 2 and m2= 2 and following formula is used to calculate correlation.

Solution SAQ 11
|
X |
dx = X - 10 |
dx2 |
Y |
dy = Y - 11 |
dy2 |
dxdy |
|
10 |
0 |
0 |
9 |
-2 |
4 |
0 |
|
6 |
-4 |
16 |
4 |
-7 |
49 |
28 |
|
9 |
-1 |
1 |
6 |
-5 |
25 |
5 |
|
10 |
0 |
0 |
9 |
-2 |
4 |
0 |
|
12 |
2 |
9 |
11 |
0 |
0 |
0 |
|
13 |
3 |
4 |
13 |
2 |
4 |
6 |
|
11 |
1 |
1 |
8 |
-3 |
9 |
-3 |
|
9 |
-1 |
1 |
4 |
-7 |
49 |
7 |
|
N = 8 |
𝛴dx = 0 |
𝛴dx2 = 32 |
N = 8 |
𝛴dy = -24 |
𝛴dy2 = 144 |
𝛴dxdy = 43 |
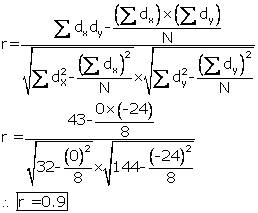
Solution SAQ 12
|
dx |
dx2 |
dy |
dy2 |
dxdy |
|
5 |
25 |
5 |
25 |
25 |
|
-4 |
16 |
-12 |
144 |
48 |
|
-2 |
4 |
-7 |
49 |
14 |
|
20 |
400 |
25 |
625 |
500 |
|
-10 |
100 |
-10 |
100 |
100 |
|
0 |
0 |
-3 |
9 |
0 |
|
3 |
9 |
0 |
0 |
0 |
|
0 |
0 |
2 |
4 |
0 |
|
-15 |
225 |
-9 |
81 |
135 |
|
-5 |
25 |
-15 |
225 |
75 |
|
𝛴 dx = -8 |
𝛴 dx2 = 804 |
𝛴 dy = -24 |
𝛴 dy2 = 1262 |
𝛴 dxdy = 897 |
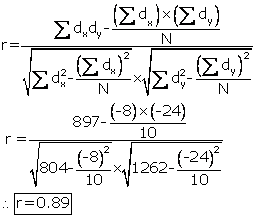
Solution SAQ 13
|
Entry |
Judge X (RX) |
Judge Y (RY) |
D = RX - RY |
D2 |
|
A |
1 |
12 |
-11 |
121 |
|
B |
2 |
9 |
-7 |
49 |
|
C |
3 |
6 |
-3 |
9 |
|
D |
4 |
10 |
-6 |
36 |
|
E |
5 |
3 |
2 |
4 |
|
F |
6 |
5 |
1 |
1 |
|
G |
7 |
4 |
3 |
9 |
|
H |
8 |
7 |
1 |
1 |
|
I |
9 |
8 |
1 |
1 |
|
J |
10 |
2 |
8 |
64 |
|
K |
11 |
11 |
0 |
0 |
|
L |
12 |
1 |
11 |
121 |
|
N = 12 |
|
|
|
𝛴 D2 = 416 |

Solution SAQ 14
|
RX |
RY |
D = RX - RY |
D2 |
|
8 |
7 |
1 |
1 |
|
7 |
5 |
2 |
4 |
|
6 |
4 |
2 |
4 |
|
3 |
1 |
2 |
4 |
|
2 |
3 |
-1 |
1 |
|
1 |
2 |
-1 |
1 |
|
5 |
6 |
-1 |
1 |
|
4 |
8 |
-4 |
16 |
|
|
|
|
𝛴D2 = 32 |

Solution SAQ 15
|
R1 |
R2 |
R3 |
D1 = R1- R2 |
D2 = R1 - R3 |
D3 = R2 - R3 |
D12 |
D22 |
D32 |
|
1 |
3 |
6 |
-2 |
-5 |
-3 |
4 |
25 |
9 |
|
6 |
5 |
4 |
1 |
2 |
1 |
1 |
4 |
1 |
|
5 |
8 |
9 |
-3 |
-4 |
-1 |
9 |
16 |
1 |
|
10 |
4 |
8 |
6 |
2 |
-4 |
36 |
4 |
16 |
|
3 |
7 |
1 |
-4 |
2 |
6 |
16 |
4 |
36 |
|
2 |
10 |
2 |
-8 |
0 |
8 |
64 |
0 |
64 |
|
4 |
2 |
3 |
2 |
1 |
-1 |
4 |
1 |
1 |
|
9 |
1 |
10 |
8 |
-1 |
-9 |
64 |
1 |
81 |
|
7 |
6 |
5 |
1 |
2 |
1 |
1 |
4 |
1 |
|
8 |
9 |
7 |
-1 |
1 |
8 |
1 |
1 |
64 |
|
|
|
|
|
|
|
𝛴D12= 200 |
𝛴D22 = 60 |
𝛴D32 = 214 |

Judges I and III have a common taste in respect of beauty as they have the highest positive rank correlation coefficient.
Correlation Exercise 334
Solution SAQ 16
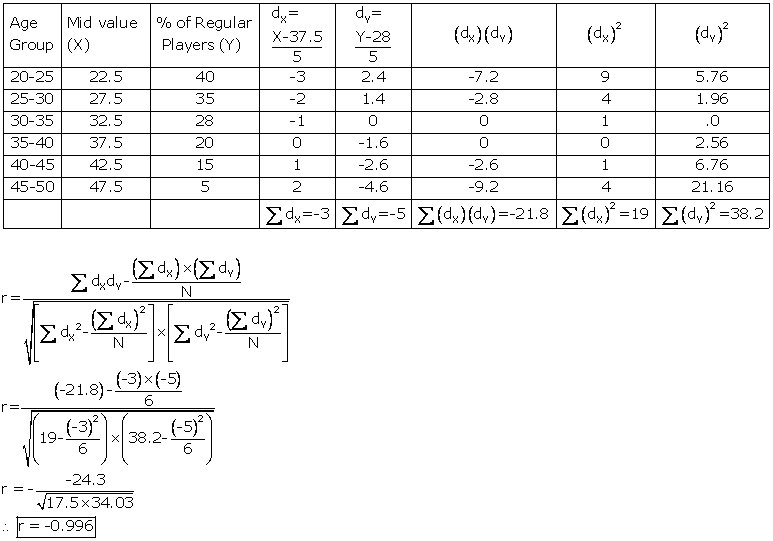
Solution SAQ 17
|
Age Group |
Mid Value (X) |
Percentage of Players (%) (Y) |
dX = X-17.5 |
dY = Y-40 |
dXdY |
dX2 |
dY2 |
|
15-16 |
15.5 |
200/250×100 = 80 |
-2 |
40 |
-80 |
4 |
1600 |
|
16-17 |
16.5 |
150/2-00×100 = 75 |
-1 |
35 |
-35 |
1 |
1225 |
|
17-18 |
17.5 |
90/150×100 = 60 |
0 |
20 |
0 |
0 |
400 |
|
18-19 |
18.5 |
48/120×100 = 40 |
1 |
0 |
0 |
1 |
0 |
|
19-20 |
19.5 |
30/100×100 = 30 |
2 |
-10 |
-20 |
4 |
100 |
|
20-21 |
20.5 |
12/80×100 = 15 |
3 |
-25 |
-75 |
9 |
625 |
|
|
N = 6 |
|
𝛴dX = 3 |
𝛴dY = 60 |
𝛴 dXdY = -210 |
𝛴dX2 = 19 |
𝛴 dY2 = 𝛴3950 |
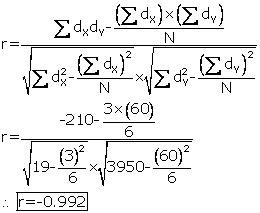
Solution SAQ 18
|
Density (X) |
dx = X - 500 |
dx2 |
|
dy = Y-1 |
dy2 |
dxdy |
|
200 |
-300 |
90000 |
2 |
1 |
1 |
-300 |
|
500 |
0 |
0 |
1 |
0 |
0 |
0 |
|
700 |
200 |
40000 |
1.3 |
0.3 |
0.09 |
60 |
|
500 |
0 |
0 |
1.4 |
0.4 |
0.16 |
0 |
|
600 |
100 |
10000 |
1.6 |
0.6 |
0.36 |
60 |
|
900 |
400 |
160000 |
1.7 |
0.7 |
0.49 |
280 |
|
|
𝛴dx=400 |
𝛴dx2=300000 |
|
𝛴dy=3 |
𝛴dy2 = 2.1 |
𝛴dxdy = 100 |
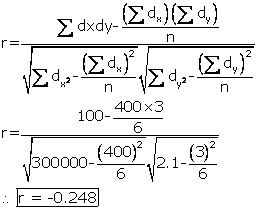
Solution SAQ 19

Solution SAQ 20