Class 10 MAHARASHTRA STATE TEXTBOOK BUREAU Solutions Maths Chapter 3 - Arithmetic Progression
Arithmetic Progression Exercise Ex. 3.1
Solution 1
(1)
In the sequence 2, 4, 6, 8, …
First term = t1 = 2, t2 = 4, t3 = 6, …
t2 - t1 = 4 - 2 = 2
t3 - t2 = 6 - 4 = 2
Here the first term is 2 and difference is constant which is 2.
∴ This sequence is an A.P.
(2)
In the sequence ![]()
First term = t1
= 2, ![]()
![]()
![]()
Here the first term
is 2 and difference is constant which is ![]()
∴ This sequence is an A.P.
(3)
In the sequence -10, -6, -2, 2, …
First term = t1 = -10, t2 = -6, t3 = -2, …
t2 - t1 = -6 - (-10) = 4
t3 - t2 = -2 - (-6) = 4
Here the first term is 2 and common difference is 4.
∴ This sequence is an A.P.
(4)
In the sequence 0.3, 0.33, 0.333, …
First term = t1 = 0.3, t2 = 0.33, t3 = 0.333, …
t2 - t1 = 0.33 - 0.3 = 0.03
t3 - t2 = 0.333 - 0.33 = 0.003
Here the difference between any two consecutive terms is not constant.
∴ This sequence is not an A.P.
(5)
In the sequence 0, -4, -8, -12, …
First term = t1 = 0, t2 = -4, t3 = -8, …
t2 - t1 = -4 - 0 = -4
t3 - t2 = -8 - (-4) = -4
Here the first term is 0 and difference is constant which is -4.
∴ This sequence is an A.P.
(6)
In the sequence ![]()
First term ![]()
![]()
![]()
Here first term is ![]() and
difference is constant which is 0.
and
difference is constant which is 0.
∴ This sequence is an A.P.
(7)
In the sequence 3, 3 + , 3 + 3 , t3 = 3 + .
∴ This sequence is an A.P.
(8)
In the sequence 127, 132, 137, …
First term t1 = 127, t2 = 132, t3 = 137
t2 - t1 = 132 - 127 = 5
t3 - t2 = 137 - 132 = 5
Here first term is 127 and difference is constant which is 5.
∴ This sequence is an A.P.
Solution 2
(1)
Given: a = 10, d = 5
t1 = 10
t2 = t1 + d = 10 + 5 = 15
t3 = t2 + d = 15 + 5 =20
t4 = t3 + d = 20 + 5 = 25
∴ A.P. is 10, 15, 20, 25, …
(2)
Given: a = -3, d = 0
t1 = -3
t2 = t1 + d = -3 + 0 = -3
t3 = t2 + d = -3 + 0 = -3
t4 = t3 + d = -3 + 0 = -3
∴ A.P. is -3, -3, -3, -3, …
(3)
Given:
![]()
t1 = -7
![]()
![]()
![]()
![]()
(4)
Given: a = -1.25, d = 3
t1 = -1.25
t2 = t1 + d = -1.25 + 3 = 1.75
t3 = t2 + d = 1.75 + 3 = 4.75
t4 = t3 + d = 4.75 + 3 = 7.75
∴ A.P. is -1.25, 1.75, 4.75, 7.75, …
(5)
Given: a = 6, d = -3
t1 = 6
t2 = t1 + d = 6 + (-3) = 3
t3 = t2 + d = 3 + (-3) = 0
t4 = t3 + d = 0 + (-3) = -3
∴ A.P. is 6, 3, 0, -3, …
(6)
Given: a = -19, d = -4
t1 = -19
t2 = t1 + d = -19 + (-4) = -23
t3 = t2 + d = -23 + (-4) = -27
t4 = t3 + d = -27 + (-4) = -31
∴ A.P. is -19, -23, -27, -31, …
Solution 3
(1)
The given A.P. is 5, 1, -3, -7, …
Here, t1 = 5, t2 = 1
d = t2 - t1 = 1 - 5 = -4
∴ First term (a) = 5 and common difference (d) = -4
(2)
The given A.P. is 0.6, 0.9, 1.2, 1.5, …
Here, t1 = 0.6, t2 = 0.9
d = t2 - t1 = 0.9 - 0.6 = 0.3
∴ First term (a) = 0.6 and common difference (d) = 0.3
(3)
The given A.P. is 127, 135, 143, 151, …
Here, t1 = 127, t2 = 135
d = t2 - t1 = 135 - 127 = 8
∴ First term (a) = 127 and common difference (d) = 8
(4)
![]()
![]()
![]()
∴ First
term (a) = ![]() and common
difference (d) =
and common
difference (d) = ![]()
Arithmetic Progression Exercise Ex. 3.2
Solution 1
(i) 1, 8, 15, 22, …
Here a = ![]() ,
t1 =
,
t1 = ![]() , t2 =
, t2 = ![]() , t3 =
, t3 = ![]() ,
,
t2 - t1
= ![]() -
- ![]() =
= ![]()
t3 - t2
= ![]() -
- ![]() =
= ![]() ∴
d =
∴
d = ![]()
(ii) 3, 6, 9, 12, ...
Here t1
= ![]() , t2 =
, t2 = ![]() ,
t3 =
,
t3 = ![]() , t4 =
, t4 = ![]() ,
,
t2 - t1
= ![]() , t3 - t2
=
, t3 - t2
= ![]() ∴
d =
∴
d = ![]()
(iii) -3, -8, -13, -18, ...
Here t1
= ![]() , t2 =
, t2 =![]() ,
t4 =
,
t4 = ![]() , t4 =
, t4 =![]() ,
,
t2 - t1
=![]() , t3 - t2
=
, t3 - t2
= ![]() ∴
a =
∴
a = ![]() , d =
, d = ![]()
(iv) 70, 60, 50, 40, …
Here t1
=![]() , t2 =
, t2 =![]() ,
t3 =
,
t3 = ![]() , …
, …
∴
a = ![]() , d =
, d = ![]()
Solution 2
The given sequence is -12, -5, 2, 9, 16, 23, 30, …
Here, t1 = -12, t2 = -5, t3 = 2, t4 = 9
∴ t2 - t1 = -5 - (-12) = 7
t3 - t2 = 2 - (-5) = 7
t4 - t3 = 9 - 2 = 7
∴ t2 - t1 = t3 - t2 = … = 7 = d
∴ This sequence is an A.P.
Now, tn = a + (n - 1)d
∴ t20 = -12 + (20 - 1)7
= -12 + 19 × 7
= -12 + 133
= 121
∴ 20th term of the given A.P. is 121.
Solution 3
Given A.P. is 12, 16, 20, 24, …
Here, t1 = a = 12, d = 16 - 12 = 4
Now, tn = a + (n - 1)d
∴ t24 = 12 + (24 - 1)4
= 12 + 23 × 4
= 12 + 92
= 104
∴ The 24th term of the given A.P. is 104.
Solution 4
Given A.P. is 7, 13, 19, 25, …
Here, t1 = a = 7, d = 13 - 7 = 6
Now, tn = a + (n - 1)d
∴ t19 = 7 + (19 - 1)6
= 7 + 18 × 6
= 7 + 108
= 115
∴ The 15th term of the given A.P. is 115.
Solution 5
Given A.P. is 9, 4, -1, -6, -11, …
Here, t1 = a = 9, d = 4 - 9 = -5
Now, tn = a + (n - 1)d
∴ t27 = 9 + (27 - 1)(-5)
= 9 + 26 × (-5)
= 9 - 130
= -121
∴ The 24th term of the given A.P. is -121.
Solution 6
The three digit natural numbers divisible by 5 are 100, 105, 110, …, 995
The above sequence is an A.P. as the difference between any two consecutive terms is constant.
∴ a = 100, d = 105 - 100 = 5
Let the number of terms in this A.P. be n.
∴ tn = 995
Now, tn = a + (n - 1)d
∴ 995 = 100 + (n - 1)5
∴ 995 - 100 = (n - 1)5
∴ 895 = (n - 1)5
∴ n - 1 = 179
∴ n = 180
∴ There are 180 three digit natural numbers which are divisible by 5.
Solution 7
Let a be the first term and d be the common difference,
Given: t11 = 16, t21 = 29
Since, tn = a + (n - 1)d
∴ t11 = a + (11 - 1)d
∴ 16 = a + 10d
∴ a + 10d = 16 … (i)
Also, t21 = a + (21 - 1)d
∴ 29 = a + 20d
∴ a + 20d = 29 …(ii)
Subtracting equation (i) from equation (ii), we get
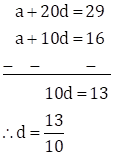
Substituting ![]() in
equation (i), we get
in
equation (i), we get
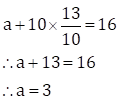
The 41st term is
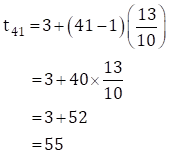
∴ t41 = 55
∴ 41st term of the A.P. is 55.
Solution 8
The given A.P. is 11, 8, 5, 2, …
Here, a = 11, d = 8 - 11 = -3
Let the nth term of this A.P. be -151.
∴ tn = -151
∴ a + (n - 1)d = -151
∴ 11 + (n - 1)(-3) = -151
∴ (n - 1)(-3) = -151 - 11
∴ (n - 1)(-3) = -162
∴ n - 1 = 54
∴ n = 55
∴ The 55th term of the given A.P. is -151.
Solution 9
The natural numbers from 10 to 250 divisible by 4 are 12, 16, 20, …, 248
The above sequence is an A.P. as the difference is constant.
∴ a = 12, d = 16 - 12 = 4
Let the total number of terms in this A.P. be n.
∴ tn = 248
Since, tn = a + (n - 1)d
∴ 248 = 12 + (n - 1)4
∴ 248 - 12 = (n - 1)4
∴ 236 = (n - 1)4
∴ n - 1 = 59
∴ n = 60
∴ There are 60 natural numbers from 10 to 250 which are divisible by 4.
Solution 10
Let a be the first term and d be the common difference of the given A.P.
As per the condition,
t17 = t10 + 7
Since, tn = a + (n - 1)d
∴ a + (17 - 1)d = a + (10 - 1)d + 7
∴ a + 16d = a + 9d + 7
∴ a + 16d - a - 9d = 7
∴ 7d = 7
∴ d = 1
Thus, the common difference is 1.
Arithmetic Progression Exercise Ex. 3.3
Solution 1
a = 6, d = 3, S27 = ?
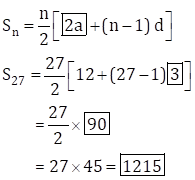
Solution 2
The even natural numbers are 2, 4, 6, 8, …
The above sequence is an A.P. as the difference between every two consecutive terms is constant.
∴ a = 2, d = 2, n = 123
We know that, ![]()
Therefore,
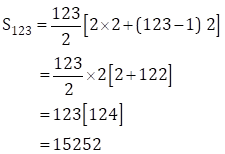
∴ Sum of first 123 even natural numbers is 15252.
Solution 3
The even numbers between 1 and 350 are 2, 4, 6, 8, …, 348.
The above sequence is an A.P. as the difference between every two consecutive terms is constant.
∴ a = 2, d = 2, tn = 348
We know that, tn = a + (n = 1)d
∴ 348 = 2 + ( n - 1)2
∴ 348 = 2 + 2n - 2
∴ 348 = 2n
∴ n = 174
Also, ![]()

∴ The sum of all even numbers between 1 and 350 is 30450.
Solution 4
Let a be the first term and d be the common difference of the A.P.
Given: t19 = 52, t38 = 128
Since, tn = a + (n - 1)d
∴ t19 = a + (19 - 1)d
∴ 52 = a + 18d
∴ a + 18d = 52 … (I)
Also, t38 = a + (38 - 1)d
∴ 128 = a + 37d
∴ a + 37d = 128 … (II)
Adding equations (I) and (II), we get
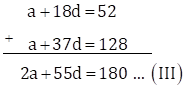
Now, ![]()
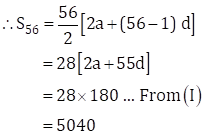
∴ The sum of first 56 terms is 5040.
Solution 5
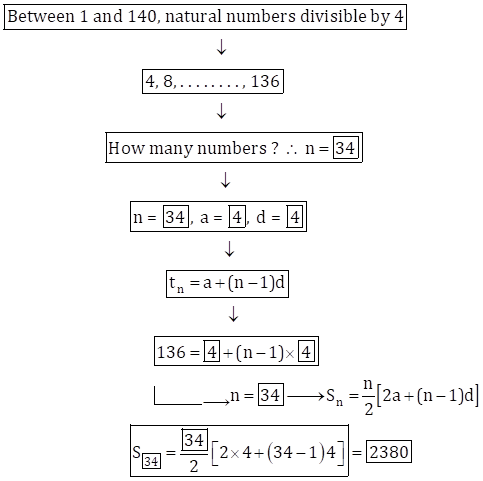
Sum of numbers from
1 to 140, which are divisible by 4 =![]() .
.
Solution 6
Let a be the first term and d be the common difference of the A.P.
Given: S55 = 3300
Since, ![]()
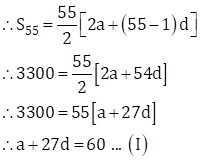
And, tn = a + (n - 1)d
∴ t28 = a + (28 - 1)d
∴ t28 = a + 27d
∴ t28 = 60 … From (I)
∴ 28th term of the A.P. is 60.
Solution 7
Let the three consecutive terms in an A.P. be a - d, a and a + d.
From the first condition, we have
a - d + a + a + d = 27
∴ 3a = 27
∴ a = 27/3
∴ a = 9 … (I)
From the second condition, we have
(a - d) a (a + d) = 504
∴ a(a2- d2) = 504
∴ 9(a2- d2) = 504 … From (I)
∴ 9(81 - d2) = 504
∴ 81 - d2 = 504/9
∴ 81 - d2 = 56
∴ d2 = 81 - 56
∴ d2 = 25
Taking square root on both the sides, we get
d = ± 5
When d = 5 and a =9, we get
a - d = 9 - 5 = 4
a = 9
a + d = 9 + 5 = 14
When d = -5 and a = 9,
a - d = 9 - (-5) = 9 + 5 = 14
a = 9
a + d = 9 - 5 = 4
∴ The three consecutive terms are 4, 9 and 14 or 14, 9 and 4.
Solution 8
Let the four consecutive terms in an A.P. be a - d, a, a + d and a + 2d.
From the first condition, we have
a - d + a + a + d + a + 2d = 12
∴ 4a + 2d =12
∴ 2(2a + d) = 12
∴ 2a + d = 12/2
∴ 2a + d = 6 … (I)
From the second condition,
a + d + a + 2d = 14
∴ 2a + 3d = 14 … (II)
Subtracting equation (I) from (II), we get
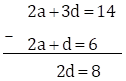
∴ d = 4
Substituting d = 4 in equation (I), we get
2a + 4 = 6
∴ 2a = 2
∴ a = 1
∴ a - d = 1 - 4 = -3
Also, a + d = 1 + 4 = 5
And, a + 2d = 1 + 8 = 9
∴ The four consecutive terms are -3, 1, 5 and 9.
Solution 9
Let a be the first term and d be the common difference of the A.P.
Given: t9 = 0
Since, tn = a + (n - 1)d
∴ t9 = a + (9 - 1)d
∴ 0 = a + 8d
∴ a = -8d … (I)
Also, t19 = a + (19 - 1)d
∴ t19 = a + 18d
∴ t19 = -8d + 18d … From (I)
∴ t19 = 10d … (II)
And, t29 = a + (29 - 1)d
i.e. t29 = a + 28d
i.e. t29 = -8d + 28d … From (I)
∴ t29 = 20d = 2(10d)
∴ t29 = 2(t19) … From (II)
∴ The 29th term is twice the 19th term.
Arithmetic Progression Exercise Ex. 3.4
Solution 1
Sanika's daily savings of 2016 are as follows:
10, 11, 12, 13, …
This is an A.P. as the difference between every two consecutive terms is constant.
∴ a = 10, d = 11 - 10 = 1
2016 is a leap year, so the number of days is 366.
∴ n =366
Now, ![]()
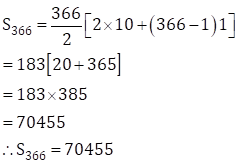
∴ Sanika' total savings on 31st Dec 2016 will be Rs. 70455.
Solution 2
Each instalment being less than the preceding one by Rs. 40.
∴ The instalments are in A.P.
Amount repaid in 12 instalments
= Amount borrowed + total interest
= 8000 + 1360
∴ S12 = 9360
Number of instalments (n) = 12
Since each instalment is less than the preceding one by Rs. 40.
∴ d = -40
Now, ![]()
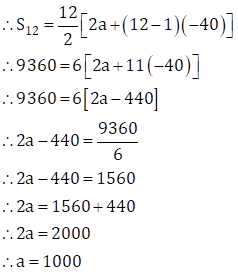
Also, tn = a + (n - 1)d
∴ t12 = 1000 + (12 - 1)(-40)
= 1000 + 11(-40)
= 1000 - 440
= 560
∴ Amount of the first and last instalments are Rs. 1000 and Rs. 560 respectively.
Solution 3
Amount invested by Sachin in each year are as follows:
5000, 7000, 9000, …
The above sequence is an A.P. as the difference between every two consecutive terms is constant.
∴ a = 5000, d = 7000 - 5000 = 2000, n = 12
Now, ![]()
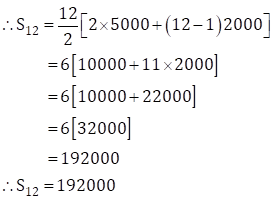
∴ The total amount that Sachin invested in 12 years is Rs. 192000.
Solution 4
The number of seats arranged row-wise are as follows:
20, 22, 24, …
The above sequence is an A.P. as the difference between every two consecutive terms is constant.
∴ a = 20, d = 22 - 20 = 2, n = 27
Now, tn = a + (n - 1)d
∴ t15 = 20 + (15 - 1)2
= 20 + 14 × 2
= 20 + 28
= 48
∴ t15 = 48
∴ The number of seats in the 15th row is 48.
Also, ![]()

∴ The total number of seats in the auditorium is 1242.
Solution 5
Let the temperatures from Monday to Saturday in A.P. be
a, a + d, a + 2d, a + 3d, a + 4d, a + 5d.
According to the first condition, we have
(a) + (a + 5d) = (a + d) + (a + 5d) + 5°
∴ d = -5°
According to the second condition, we have
a + 2d = -30°
∴ a + 2(-5°) = -30°
∴ a - 10° = -30°
∴ a = -30° + 10° = -20°
∴ a + d = -20° - 5° = -25°
a + 3d = -20° + 3(-5°) = -20° - 15° = -35°
a + 4d = -20° + 4(-5°) = -20° - 20° = -40°
a + 5d = -20° + 5(-5°) = -20° - 25° = -45°
∴ The temperatures on the other five days are
-20°C, -25° C, -35° C, -40° C and -45° C.
Solution 6
The number of trees planted row-wise are as follows:
1, 2, 3, …
The above sequence is an A.P. as the difference between every two consecutive terms is constant.
∴ a = 1, d = 2 - 1 = 1, n = 25
Now, ![]()
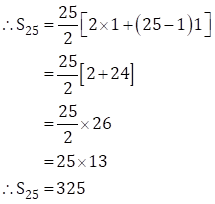
∴ The total number of trees in 25 rows is 325.
Arithmetic Progression Exercise Problem Set 3
Solution 1(1)
In the sequence -10, -6, -2, 2, …
First term = t1 = -10, t2 = -6, t3 = -2, …
t2 - t1 = -6 - (-10) = 4
t3 - t2 = -2 - (-6) = 4
Here the first term is -10 and difference is constant which is 4.
∴ This sequence is an A.P. and the reason is d = 4.
Solution 1(2)
Given: first term (a) = -2 and common difference (d) = -2
t1 = -2
t2 = t1 + d = -2 - 2 = -4
t3 = t2 + d = -4 - 2 = -6
t4 = t3 + d = -6 - 2 = -8
∴ First four terms of the A.P. are -2, -4, -6, -8.
Solution 1(3)
The first 30 natural numbers are 1, 2, 3, …, 30.
The above sequence is an A.P. as the difference between every two consecutive terms is constant.
∴ a = 1, d = 2 - 1 = 1, n = 30
Now, ![]()

∴ The sum of the first 30 natural numbers is 465.
Solution 1(4)
Given: t7 = 4, d = -4
Now, tn = a + (n - 1)d
∴ t7 = a + (7 - 1)(-4)
∴ 4 = a + 6(-4)
∴ 4 = a - 24
∴ a = 4 + 24
∴ a = 28
Solution 1(5)
Given: a = 3.5, d = 0, n = 101
Now, tn = a + (n - 1)d
∴ t101 = 3.5 + (101 - 1)(0)
= 3.5 + 100×0
= 3.5 + 0
= 3.5
∴ t101 = 3.5
Solution 1(6)
Given: a = t1 = -3, t2 = 4
Here, d = t2 - t1 = 4 - (-3) = 4 + 3 = 7
Now, tn = a + (n - 1)d
∴ t21 = -3 + (21 - 1)(7)
= -3 + 20×7
= -3 + 140
= 137
∴ 21st term is 137.
Solution 1(7)
Given: d = 5
Now, tn = a + (n - 1)d
∴ t18 - t13 = a + (18 - 1)d - [a + (13 - 1)d]
= a + 17d - [a + 12d]
= a + 17d - a - 12d
= 5d
= 5×5
= 25
∴ t18 - t13 = 25
Solution 1(8)
First five multiples of 3 are 3, 6, 9, 12, 15.
The above sequence is an A.P.as the difference between every two consecutive terms is constant.
∴ a = 3, d = 6 - 3 = 3, n = 5
Now, ![]()
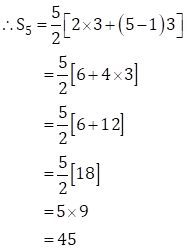
∴ Sum of first five multiples of 3 is 45.
Solution 1(9)
The sequence is 15, 10, 5, …
The above sequence is an A.P. as the difference between every two consecutive terms is constant.
∴ a = 15, d = 10 - 15 = -5, n = 10
Now, ![]()
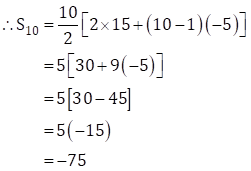
∴ The sum of first 10 terms is -75.
Solution 1(10)
Given: First term (t1) = 1, last term (tn) = 20, Sn = 399
Now, ![]()

Solution 2
The given A.P. is -11, -8, -5, …, 49
Reversing the above A.P., we get 49, …, -5, -8, -11
This is also an A.P.
Here, a = 49, d = -11 - (-8) = -11 + 8 = -3
Now, tn = a + (n - 1)d
∴ t4 = 49 + (4 - 1)(-3)
= 49 + (3)(-3)
= 49 - 9
= 40
∴ Fourth term from the end in the given A.P. is 40.
Solution 3
Let a be the first term and d be the common difference of the A.P.
Given: t10 = 46, t5 + t7 = 52
Since, tn = a + (n - 1)d
∴ t10 = a + (10 - 1)d
∴ 46 = a + 9d
i.e. a + 9d = 46 … (I)
Also, t5 + t7 = 52
∴ a + (5 - 1)d + a + (7 - 1)d = 52
∴ a + 4d + a + 6d = 52
∴ 2a + 10d = 52
∴ 2 (a + 5d) = 52
Dividing both the sides by 2, we get
a + 5d = 26 … (II)
Subtracting equation (II) from (I), we get
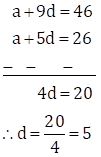
Substituting d = 5 in equation (II), we get
a + 5×5 = 26
∴ a + 25 = 26
∴ a = 26 - 25
∴ a = 1
∴ t1 = a = 1
t2 = t1 + d = 1 + 5 = 6
t3 = t2 + d = 6 + 5 = 11
t4 = t2 + d = 11 + 5 = 116
∴ The required A.P. is 1, 6, 11, 16, …
Solution 4
Given: t4 = -15, t9 = -30
Now, tn = a + (n - 1)d
∴ t4 = a + (4 - 1)d
∴ -15 = a + 3d
∴ a + 3d = -15 … (I)
And, t9 = a + (9 - 1)d
∴ -30 = a + 8d
∴ a + 8d = -30 … (II)
Subtracting equation (I) from (II), we get
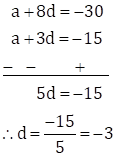
Substituting d = -3 in equation (I), we get
a + 3×(-3) = -15
∴ a - 9 = -15
∴ a = -15 + 9
∴ a = -6
Since, ![]()
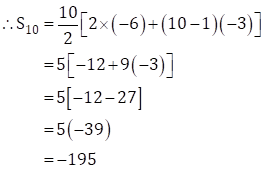
∴ The sum of the first 10 numbers is -195.
Solution 5
The first A.P. is 9, 7, 5, …
Here, a = 9, d = 7 - 9 = -2
Now, nth term = tn = a + (n - 1)d
∴ nth term = 9 + (n - 1) (-2)
= 9 - 2n + 2
= 11 - 2n
The second A.P. is 24, 21, 18, …
Here, a = 24, d = 21 - 24 = - 3
∴ nth term = a + (n - 1)d
= 24 + (n - 1) (-3)
= 24 - 3n + 3
= 27 - 3n
Since, the nth terms of the two A.P.'s are equal.
∴ 11 - 2n = 27 - 3n
∴ 3n - 2n = 27 - 11
∴ n = 16
∴ t16 = 9 + (16 - 1) (-2)
= 9 + 15 × (-2)
= 9 - 30
∴ t16 = -21
∴ The values of n and nth term are 16 and -21 respectively.
Solution 6
Let 'a' be the first term and d be the common difference of the A.P.
As per the first condition, we have
t3 + t8 = 7
Since, tn = a + (n - 1)d
∴ a + (3 - 1) d + a + (8 - 1)d = 7
∴ a + 2d + a + 7d = 7
∴ 2a + 9d = 7 … (I)
As per the second condition, we have
t7 + t14 = -3
∴ a + (7 - 1)d + a + (14 - 1 )d = -3
∴ a + 6d + a + 13d = -3
∴ 2a + 19 d = - 3 … (II)
Subtracting equation (I) from (II), we get
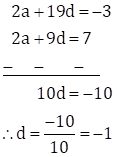
Substituting d = -1 in equation (I), we get
2a + 9×(-1) = 7
∴ 2a - 9 = 7
∴ 2a = 7 + 9
∴ 2a = 16
∴ a = 8
∴ t10 = 8 + (10 - 1)(-1)
= 8 + 9(-1)
= 8 - 9
= -1
∴ The 10th term of the A.P. is -1.
Solution 7
Let the number of terms in the A.P. be n and the common difference be 'd'.
∴ a = -5, tn = 45, Sn = 120 … (Given)
Now, tn = a + (n - 1)d
∴ 45 = -5 + (n - 1)d
∴ 45 + 5 = (n - 1)d
∴ (n - 1)d = 50 … (I)
Since, ![]()
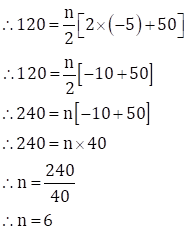
Substituting n = 6 in equation (I), we get
(6 - 1)d = 50
∴ 5d = 50
![]()
∴ d = 10
∴ The number of terms is 6 and the common difference is 10.
Solution 8
The natural numbers from 1 to n are 1, 2, 3, …, n.
The above sequence is an A.P. as the difference between every two consecutive terms is constant.
∴ a = 1, d = 2 - 1 = 1
Also, Sn = 36 …[Given]
Since, ![]()

∴ 72 = n2 + n
∴ n2 + n - 72 = 0
∴ n2 + 9n - 8n - 72 = 0
∴ n(n + 9) - 8 (n + 9) = 0
∴ (n + 9) (n - 8) = 0
∴ n + 9 = 0 or n - 8 = 0
∴ n = -9 or n = 8
But, number of terms cannot be negative.
∴ n = 8
∴ The value of n is 8.
Solution 9
Let the three parts of 207 be a - d, a, a + d.
As per the first condition, we have
(a - d) + a + (a + d) = 207
∴ 3a = 207
![]()
∴ a = 69 … (I)
As per the second condition, we have
(a - d) × a = 4623
∴ (69 - d) × 69 = 4623 … [From (I)]
![]()
∴ 69 - d = 67
∴ d = 69 - 67
∴ d = 2
∴ a - d = 69 - 2 = 67
a = 69
a + d = 69 + 2 = 71
∴ The three parts of 207 that are in A.P. are 67, 69 and 71.
Solution 10
The number of terms is 37.
∴ Middle term ![]()
∴ The terms 18th, 19th and 20th are placed exactly at the middle.
As per the first condition, we have
t18 + t19 + t20 = 225
Since, tn = a + (n - 1)d
∴ a + (18 - 1)d + a + (19 - 1)d + a + (20 - 1)d = 225
∴ 3a + 17d + 18d + 19d = 225
∴ 3a + 54d = 225 … (I)
As per the second condition, we have
t35 + t36 + t37 = 429
∴ a + (35 - 1)d + a + (36 - 1)d + a + (37 - 1)d = 429
∴ 3a + 34d + 35d + 36d = 429
∴ 3a + 105d = 429 … (II)
Subtracting equation (I) from (II), we get
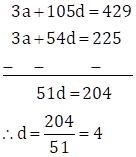
Substituting d = 4 in equation (I), we get
3a + 54 × 4 = 225
∴ 3a + 216 = 225
∴ 3a = 225 - 216
∴ 3a = 9
∴ a = 3
∴ The required A.P. is 3, 3 + 4, 3 + 2×4, 3 + 3×4, …, 3 + (37 - 1)4
i.e. 3, 7, 11, 15, …, 144.
Solution 11
Given: t1 = a, t2 = b, tn = c
∴ d = t2 - t1 = b - a
Since, tn = a + (n - 1)d
∴ c = a + (n - 1)(b - a)
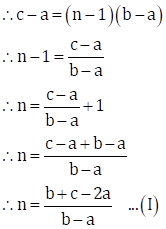
Now, ![]()
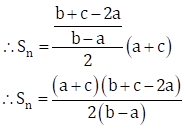
Solution 12
Let a be the first term and d be the common difference of the A.P.
The sum of first n terms of an A.P. is given by
![]()
As per the given condition, we have
Sp = Sq
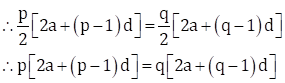
∴ 2ap + p(p - 1)d = 2aq + q(q - 1)d
∴ 2ap + p2d - pd = 2aq + q2d - qd
∴ 2ap - 2aq + p2d - q2d - pd + qd = 0
∴ 2a(p - q) + d(p2 - q2) - d(p - q) =
Since, a2 - b2 = (a + b)(a - b)
∴ 2a(p - q) + d(p + q)(p - q) - d(p - q) = 0
∴ (p - q)[2a + d(p + q) - d] = 0
∴ (p - q)[2a + d(p + q - 1)] = 0
∴ (p - q) = 0 or [2a + d(p + q - 1)] = 0
But p ≠ q
∴ 2a + d(p + q - 1) = 0 … (I)
Now, sum of (p + q) terms is
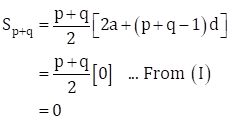
∴ The sum of first (p + q) terms is 0.
Solution 13
As per the given condition, we have
m × tm = n × tn
Since, tn = a + (n - 1)d
∴ m[a + (m - 1)d] = n[a + (n - 1)d]
∴ ma + md(m - 1) = na + nd(n - 1)
∴ ma + m2d - md = na + n2d - nd
∴ ma + m2d - md - na - n2d + nd = 0
∴ (ma - na) + (m2d - n2d) - (md - nd) = 0
∴ a(m - n) + d(m2- n2) - d(m - n) = 0
Since, a2 - b2 = (a + b)(a - b)
∴ a(m - n) + d(m + n) (m - n) - d(m - n) = 0
∴ (m - n)[a + (m + n - 1) d] = 0
∴ m - n = 0 or [a+ (m + n - 1)d] = 0
But m ≠ n
∴ a + (m + n - 1)d = 0
∴ t(m+n) = 0
∴ The (m + n)th term of the A.P. is 0.
Solution 14
Simple interest = ![]()
Simple interest
after 1 year =![]()
Simple interest
after 2 year =![]()
Simple interest
after 3 year = ![]()
According to this
the simple interest for 4, 5, 6 years will be 400,![]() ,
,![]() respectively.
respectively.
From this d =![]() , and a =
, and a =![]()
Amount of simple interest after 20 years
tn= a + (n - 1)d
t20 =![]() +
(20 - 1)
+
(20 - 1) ![]()
t20 =![]()
Amount of simple
interest after 20 years is = ![]()

