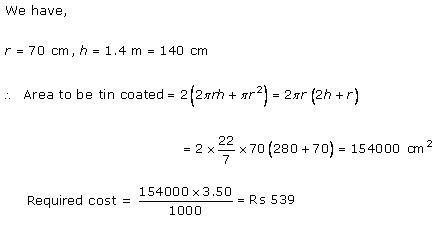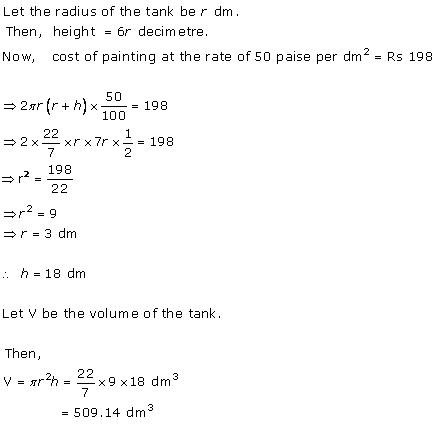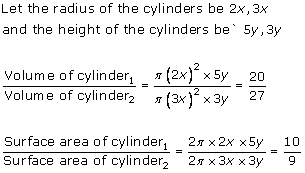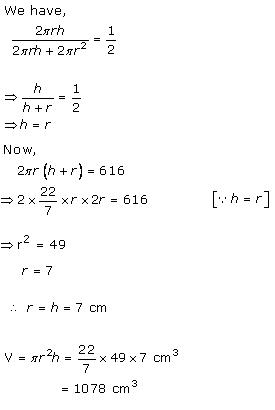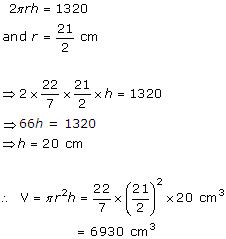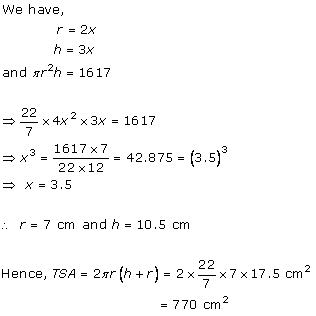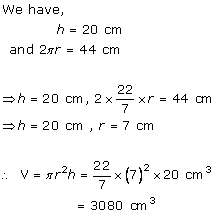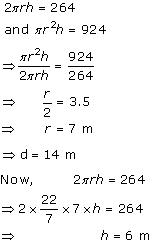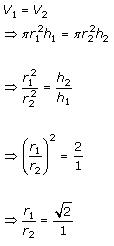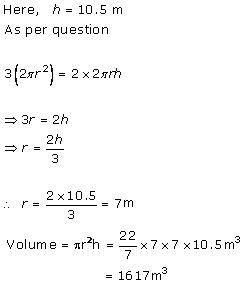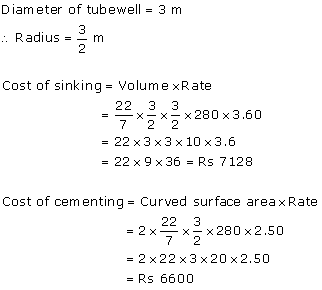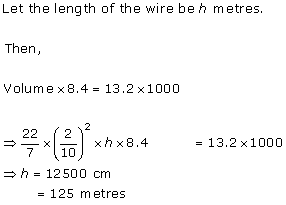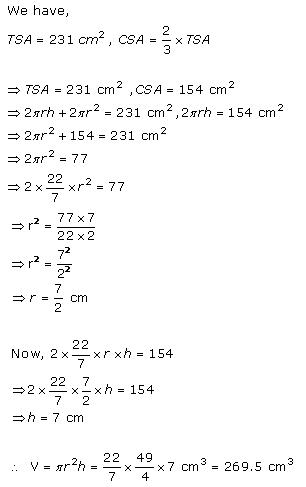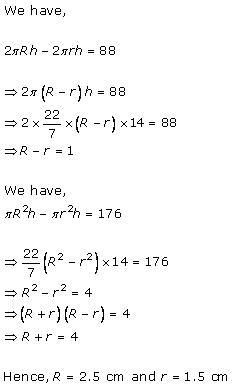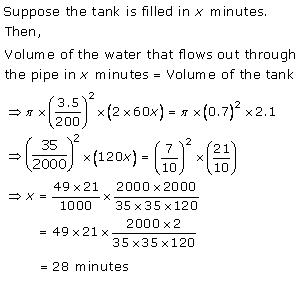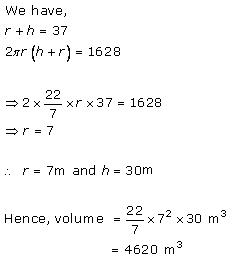Class 9 RD SHARMA Solutions Maths Chapter 19 - Surface Areas and Volume of a Circular Cylinder
Surface Areas and Volume of a Circular Cylinder Exercise Ex. 19.1
Solution 1

Solution 2
Radius (r) of circular end of pipe =
CSA of cylindrical pipe =
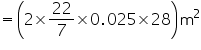 = 4.4
= 4.4 Thus, the area of radiating surface of the system is 4.4 m2 or 44000 cm2.
Solution 3
Radius of the circular end of the pillar =
CSA of pillar =
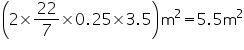
Cost of painting 1
Cost of painting 5.5
Thus, the cost of painting the CSA of pillar is Rs 68.75.
Solution 4
Base radius (r) of cylindrical tank =
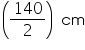 = 70 cm = 0.7 m
= 70 cm = 0.7 mArea of sheet required = total surface area of tank =
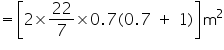
So, it will require 7.48
Solution 5
Solution 6
Solution 7
Solution 8
Depth (h) of circular well = 10 m
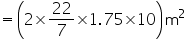
= (44 x 0.25 x 10)
= 110 m2
Cost of plastering 110 m2 area = Rs (110 x 40) = Rs 4400
Solution 9
Height of penholder = 10.5 cm
Surface area of 1 penholder = CSA of penholder + Area of base of
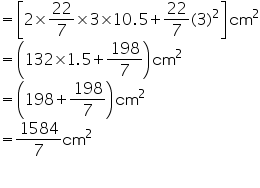
Area of cardboard sheet used by 1 competitor =
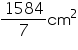
Area of cardboard sheet used by 35 competitors
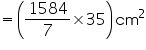 = 7920 cm2
= 7920 cm2Thus, 7920 cm2 of cardboard sheet will be required for the competition.
Solution 10

Solution 11
Solution 12
Solution 13
Solution 14
Radius (r) of circular end of cylindrical tank =
 m = 2.1m
m = 2.1m(i) Lateral or curved surface area of tank =
=
= 59.4 m2
(ii) Total surface area of tank = 2
=
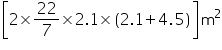
= 87.12 m2
Let A m2 steel sheet be actually used in making the tank.
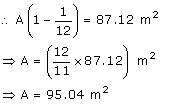
Thus, 95.04
Surface Areas and Volume of a Circular Cylinder Exercise Ex. 19.2
Solution 1
Breadth (b) of tin can = 4 cm
Height (h) of tin can = 15 cm
Capacity of tin can = l
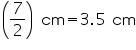
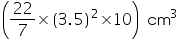 =385 cm3
=385 cm3Difference in capacity = (385 - 300) cm3 = 85 cm3
Solution 2
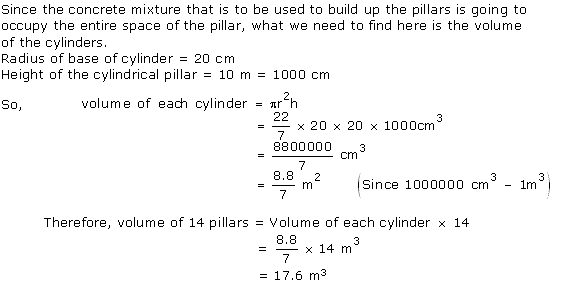
Solution 3

Solution 4
Let radius of cylinder be r.
CSA of cylinder = 94.2 cm2
2
(2
r = 3 cm
Solution 5
Height (h) of the cylindrical vessel = 1 m
Volume of cylindrical vessel = 15.4 litres = 0.0154 m3
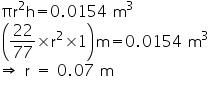
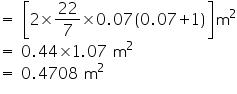
Solution 6
Height (h) up to which the bowl is filled with soup = 4 cm

Volume of soup in 250 bowls = (250
Thus, the hospital will have to prepare 38.5 litres of soup daily to serve 250 patients.
Solution 7

Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
Solution 13
Solution 14
Solution 15
Solution 16
Solution 17
Solution 18
Solution 19
Solution 20
Solution 21
Solution 22
Solution 23
Solution 24
Solution 25
Solution 26
Solution 27
Solution 28
Solution 29
Solution 30
Solution 31
Solution 32
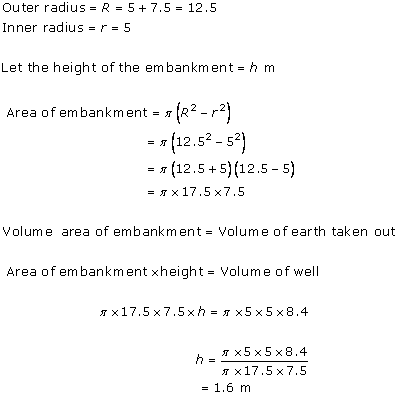
Surface Areas and Volume of a Circular Cylinder Exercise 19.28
Solution 1

Solution 2

Solution 3
Number of Surfaces In a Right cylinder are 3.
Top surface, bottom surface and curved surface.
Hence, correct option is (c).
Solution 4
Vertical cross-section of cylinder will always be a Rectangle of sides 'h', and 'r',
where h is the height of a cylinder and r is the radius of a cylinder.
Hence, correct option is (b).
Solution 5
Volume of cylinder
= Area of Base × Height
= (∏r2) × h
V = ∏r2h
Hence, correct option is (b).
Solution 6
A Hollow cylinder has only 2 surfaces.
One is outer-curved surface and another is inner-curved surface.
Hence, correct option is (b).
Surface Areas and Volume of a Circular Cylinder Exercise 19.29
Solution 7
Volume of a cylinder = V = ∏r2h
If r' = 2r and h' = h, then
V' = ∏(2r)2h = 4∏r2h
V' = 4V
Hence, correct option is (d).
Solution 8
Volume of cylinder V = ∏r2h
If h' = 2h and r' = r, then
V' = ∏(r)2(2h) = 2∏r2h = 2V
Hence, correct option is (a).
Solution 9

Solution 14

Solution 15

Solution 16

Solution 10

Solution 11

Solution 12

Solution 13

Solution 17
Total surface Area = Area of Top + Area of bottom + Curved Surface Area
T.S.A. = ∏r2 + ∏r2 + 2∏rh = 2∏r2 + 2∏rh = 2∏r (r + h)
Hence, correct option is (a).
Surface Areas and Volume of a Circular Cylinder Exercise 19.30
Solution 18

Solution 19

Solution 20