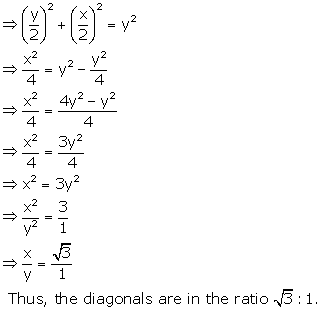Class 9 SELINA Solutions Maths Chapter 12: Mid-point and Its Converse [ Including Intercept Theorem]
Mid-point and Its Converse [ Including Intercept Theorem] Exercise Ex. 12(A)
Solution 1(a)
Correct option: (iv) 10 cm
In right-angled ΔADC,
AC2 = AD2 + CD2 = 162 + 122 = 256 + 144 = 400
⇒ AC = 20 cm
Now, in ΔABC, P and Q are the mid-points of sides AB and BC respectively.
Then, by Mid-point Theorem,
Solution 1(b)
Correct option: (iii) parallelogram
Consider a quadrilateral PQRS.
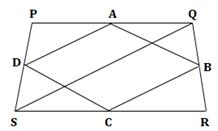
A, B, C and D are the mid-points of sides PQ, QR, RS and SP respectively.
QS is the diagonal of quadrilateral PQRS.
In ΔPSQ,
![]() [By Mid-point Theorem]
[By Mid-point Theorem]
In ΔRSQ,
![]() [By Mid-point
Theorem]
[By Mid-point
Theorem]
Therefore, ![]()
Similarly, it can
be proved that ![]()
Hence, ABCD is a parallelogram.
Solution 1(c)
Correct option: (i) 31.8 cm
In ΔABC, X and Y are the mid-points of sides AB and AC respectively.
Then, by Mid-point Theorem,
Now,
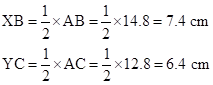
Therefore, the perimeter of quadrilateral BCYX
= BC + CY + YX + XB
= (12 + 6.4 + 6 + 7.4) cm
= 31.8 cm
Solution 1(d)
Correct option: (ii) isosceles
P, Q and R are the mid-points of sides BC, CA and AB respectively.
Then, by Mid-point Theorem,
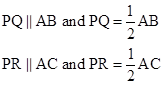
But, AB = AC (given)
∴ PQ = PR
Therefore, ΔPQR is an isosceles triangle.
Solution 1(e)
Correct option: (ii) rhombus
Construction: Draw diagonals AC and BD.
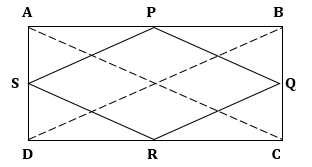
In ΔABC, P and Q are the mid-points of sides AB and BC respectively.
Then, by Mid-point Theorem,
![]() (I)
(I)
Also, in ΔADC, S and R are the mid-points of sides AD and CD respectively.
Then, by Mid-point Theorem,
![]() (II)
(II)
Similarly, it can be proved that
![]() (III)
(III)
![]() (IV)
(IV)
Now, AC = BD (diagonals of a rectangle are equal)
Therefore, from equations (I), (II), (III) and (IV),
PQ = QR = RS = SP
Hence, quadrilateral PQRS is a rhombus.
Solution 2
The triangle is shown below,
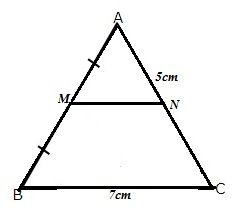
Since M is the midpoint of AB and MN||BC hence N is the midpoint of AC.Therefore
![]()
And ![]()
Solution 3
The figure is shown below,
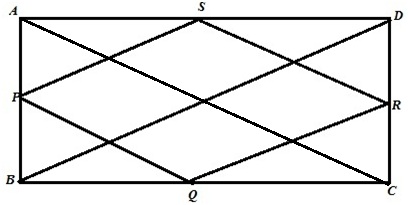
Let ABCD be a rectangle where P,Q,R,S are the midpoint of AB,BC, CD, DA.We need to show that PQRS is a rhombus
For help we draw two diagonal BD and AC as shown in figure
Where BD=AC(Since diagonal of rectangle are equal)
Proof:
From ![]() and
and ![]()
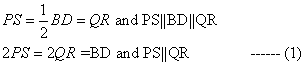
Similarly 2PQ=2SR=AC and PQ||SR----- (2)
From (1) and (2) we get
PQ=QR=RS=PS
Therefore PQRS is a rhombus.
Hence proved
Solution 4
The figure is shown below

Given that ABC is an isosceles triangle where AB=AC.
Since D,E,F are midpoint of AB,BC,CA therefore
2DE=AC and 2EF=AB this means DE=EF
Therefore DEF is an isosceles triangle an DE=EF.
Hence proved
Solution 5
Here from triangle ABD P is the midpoint of AD and PR||AB, therefore Q is the midpoint of BD
Similarly R is the midpoint of BC as PR||CD||AB
From triangle ABD 2PQ=AB …….(1)
From triangle BCD 2QR=CD …..(2)
Now (1)+(2)=>
2(PQ+QR)=AB+CD
![]()
Hence proved
Solution 6
Let we draw a diagonal AC as shown in the figure below,
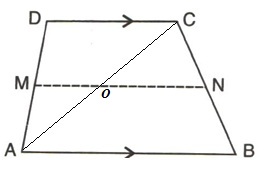
(i)Given that AB=11cm,CD=8cm
From triangle ABC
![]()
From triangle ACD
![]()
Hence MN=OM+ON=(4+5.5)=9.5cm
(ii)Given that CD=20cm,MN=27cm
From triangle ACD
![]()
Therefore ON=27-10=17cm
From triangle ABC
![]()
(iii)Given that AB=23cm,MN=15cm
From triangle ABC
![]()
Therefore OM=15-11.5=3.5cm
From triangle ACD
![]()
Solution 7
The figure is shown below
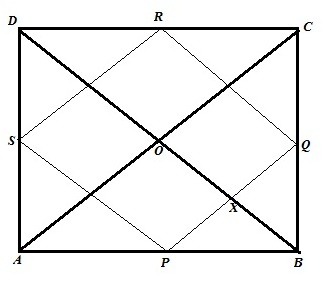
Let ABCD be a quadrilateral where P,Q,R,S are the midpoint of AB,BC,CD,DA. Diagonal AC and BD intersects at right angle at point O. We need to show that PQRS is a rectangle
Proof:
From ![]() and
and ![]()
2PQ=AC and PQ||AC …..(1)
2RS=AC and RS||AC …..(2)
From (1) and (2) we get,
PQ=RS and PQ||RS
Similarly we can show that PS=RQ and PS||RQ
Therefore PQRS is a parallelogram.
Now PQ||AC, therefore ![]()
Again BD||RQ, therefore ![]()
Similarly ![]()
Therefore PQRS is a rectangle.
Hence proved
Solution 8
The required figure is shown below
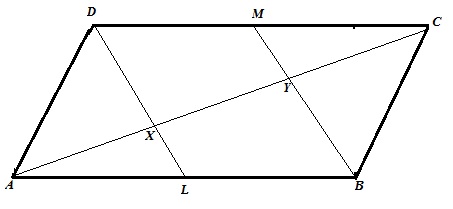
From figure,
BL=DM and BL||DM and BLMD is a parallelogram, therefore BM||DL
From triangle ABY
L is the midpoint of AB and XL||BY, therefore x is the midpoint of AY.ie AX=XY …..(1)
Similarly for triangle CDX
CY=XY …..(2)
From (1) and (2)
AX=XY=CY and AC=AX+XY+CY
Hence proved
Solution 9
Given that AD=BC …..(1)
From the figure,
For triangle ADC and triangle ABD
2GH=AD and 2EF=AD, therefore 2GH=2EF=AD …..(2)
For triangle BCD and triangle ABC
2GF=BC and 2EH=BC, therefore 2GF=2EH=BC …..(3)
From (1),(2),(3) we get,
2GH=2EF=2GF=2EH
GH=EF=GF=EH
Therefore EFGH is a rhombus.
Hence proved
Solution 10
For help we draw the diagonal BD as shown below
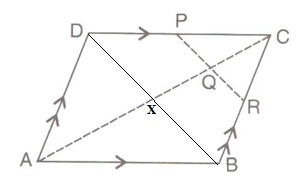
The diagonal AC and BD cuts at point X.
We know that the diagonal of a parallelogram intersects equally each other. Therefore
AX=CX and BX=DX
Given,
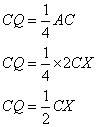
Therefore Q is the midpoint of CX.
(i)For triangle CDX PQ||DX or PR||BD
Since for triangle CBX
Q is the midpoint of CX and QR||BX. Therefore R is the midpoint of BC
(ii)For triangle BCD
As P and R are the midpoint of CD and BC ,therefore ![]()
Solution 11
The required figure is shown below

For triangle ABC and OBC
2DE=BC and 2PQ=BC, therefore DE=PQ …..(1)
For triangle ABO and ACO
2PD=AO and 2FQ=AO, therefore PD=FQ …..(2)
From (1),(2) we get that PQFD is a parallelogram.
Hence proved
Solution 12
The required figure is shown below
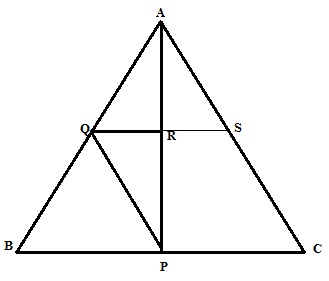
From the figure it is seen that P is the midpoint of BC and PQ||AC and QR||BC
Therefore Q is the midpoint of AB and R is the midpoint of AP
(i)Therefore AP=2AR
(ii)Here we increase QR so that it cuts AC at S as shown in the figure.
(iii)From triangle PQR and triangle ARS

![]()
Therefore QR=RS
Now
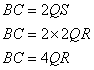
Hence proved
Solution 13
The required figure is shown below
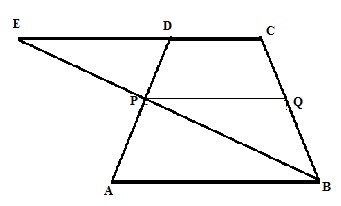
(i)

(ii)For triangle ECB PQ||CE
Again CE||AB
Therefore PQ||AB
Hence proved
Solution 14
The required figure is shown below

For help we draw a line DG||BF
Now from triangle ADG, DG||BF and E is the midpoint of AD
Therefore F is the midpoint of AG,ie AF=GF …..(1)
From triangle BCF, DG||BF and D is the midpoint of BC
Therefore G is the midpoint of CF,ie GF=CF …(2)
AC=AF+GF+CF
AC=3AF(From (1) and (2))
Hence proved
Solution 15
The required figure is shown below
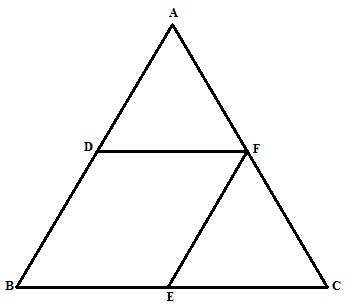
(i)Since F is the midpoint and EF||AB.
Therefore E is the midpoint of BC
So ![]() and
and ![]() …..(1)
…..(1)
Since D and F are the midpoint of AB and AC
Therefore DE||BC
SO ![]() and
and ![]() …..(2)
…..(2)
From (1),(2) we get
BE=DF and BD=EF
Hence BDEF is a parallelogram.
(ii)Since
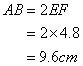
Solution 16
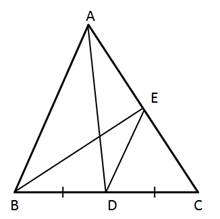

Mid-point and Its Converse [ Including Intercept Theorem] Exercise Ex. 12(B)
Solution 1(a)
Correct option: (iii) 6.3 cm
Line ![]()
Also, D is the mid-point of CE.
Then, by converse of Mid-point Theorem, B is the mid-point of AC.
Now, in ΔACE, B and
D are mid-points of sides AC and CE and ![]() .
.
Then, by Mid-point theorem,
![]()
Solution 1(b)
Correct option: (ii) 2EF = AB + DC
Consider trapezium ABCD as follows:

AC is the diagonal of trapezium ABCD intersecting EF at point G.
E and F are the mid-points of sides AD and BC respectively.
![]()
In ΔADC, E is the mid-point of AD and ![]() .
.
Then, by converse of Mid-point theorem, G is the mid-point of AC.
Therefore, by Mid-point theorem,
![]()
Also, ![]()
In ΔABC, F and G are mid-points of BC and AC and ![]() .
.
Therefore, by Mid-point theorem,
![]()
Adding equations (I) and (II),
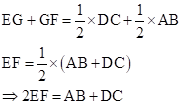
Solution 1(c)
Correct option: (iv) AB
In ΔADF, E is the
mid-point of AD and ![]() .
.
Then, by converse of Mid-point theorem, B is the mid-point of AF.
∴ BF = AB
Solution 1(d)
Correct option:
(ii) ![]()
AD and BE are medians.
⇒ E and D are the mid-points of AC and BC.
In ΔACB, E and D are mid-points of sides AC and BC.
Then, by Mid-point theorem,
![]()
Solution 1(e)
Correct option: (ii) 12 cm
In every trapezium, the length of the line segment joining the mid-points of the non-parallel sides is equal to half of the sum of lengths of the parallel sides.
So,
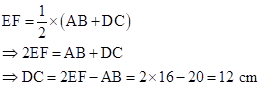
Solution 2
According to equal intercept theorem since CD=DE
Therefore AB=BC and EF=GF
(i)BC=AB=7.2cm
(ii)GE=EF+GF=2EF=![]() =8cm
=8cm
Since B,D,F are the midpoint and AE||BF||CG
Therefore AE=2BD and CG=2DF
(iii)AE=2BD=![]() =8.2
=8.2
(iv)![]()
Solution 3
Given that AD=AP=PB as 2AD=AB and p is the midpoint of AB
(i)From triangle DPR, A and Q are the midpoint of DP and DR.
Therefore AQ||PR
Since PR||BS ,hence AQ||BS
(ii)From triangle ABC, P is the midpoint and PR||BS
Therefore R is the midpoint of BC
DS=DQ+QR+RS=QR+QR+RS=3RS
Solution 4
Consider the figure:
Here D is the midpoint of BC and DP is parallel to AB, therefore P is the midpoint of AC and ![]()
(i)
Again from the triangle AEF we have AE ||PD||CR and ![]()
Therefore ![]() or we can say that 3DF = EF .
or we can say that 3DF = EF .
Hence it is shown.
(ii)
From the triangle PED we have PD||CR and C is the midpoint of PE therefore ![]()
Now
Hence it is shown.
Solution 5
The figure is shown below
(i)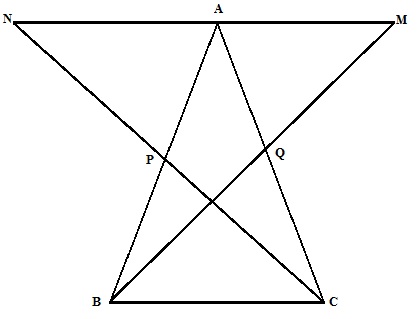
From triangle BPC and triangle APN

And BC=AN ……(3)
Similarly ![]() …..(2)
…..(2)
And BC=AM ……(4)
Now
![]()
Therefore M,A,N are collinear
(ii) From (3) and (4) MA=NA
Hence A is the midpoint of MN
Solution 6
The figure is shown below
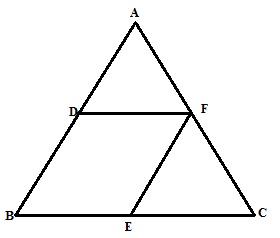
From the figure EF||AB and E is the midpoint of BC.
Therefore F is the midpoint of AC.
Here EF||BD, EF=BD as D is the midpoint of AB
BE||DF, BE=DF as E is the midpoint of BC.
Therefore BEFD is a parallelogram.
Solution 7
The figure is shown below
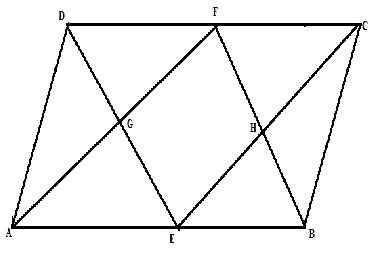
(i)

(ii)
Similarly AG=GF and EG=DG …..(1)
For triangle ECD, F and H are the midpoint of CD and EC.
Therefore HF||DE and ![]() …..(2)
…..(2)
(1),(2) we get, HF=EG and HF||EG
Similarly we can show that EH=GF and EH||GF
ThereforeGEHF is a parallelogram.
Solution 8
The figure is shown below
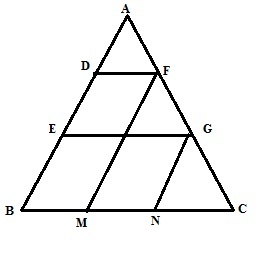
For triangle AEG
D is the midpoint of AE and DF||EG||BC
Therefore F is the midpoint of AG.
AF=GF …..(1)
Again DF||EG||BC DE=BE, therefore GF=GC …..(2)
(1),(2) we get AF=GF=GC.
Similarly SinceGN||FM||AB and AF=GF ,therefore BM=MN=NC
Hence proved
Solution 9
The figure is shown below
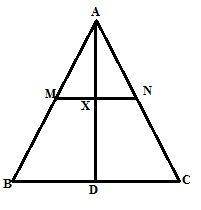
Since M and N are the midpoint of AB and AC, MN||BC
According to intercept theorem Since MN||BC and AM=BM,
Therefore AX=DX. Hence proved
Solution 10
The figure is shown below
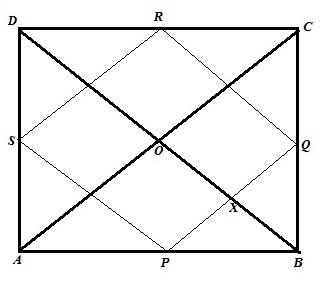
Let ABCD be a quadrilateral where P,Q,R,S are the midpoint of AB,BC,CD,DA.PQRS is a rectangle. Diagonal AC and BD intersect at point O. We need to show that AC and BD intersect at right angle.
Proof:
PQ||AC, therefore ![]() ….(1)
….(1)
||Again BD||RQ, therefore ![]() …(2)
…(2)
From (1) and (2) we get ,
![]()
Similarly ![]()
Therefore diagonals AC and BD intersect at right angle
Hence proved
Mid-point and Its Converse [ Including Intercept Theorem] Exercise Test Yourself
Solution 1
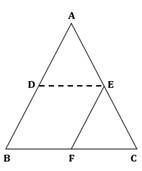
In ΔABC, D and E are mid-points of the sides AB and AC respectively.
Then, by Mid-point theorem,
![]()
Also, ![]()
Hence, BDEF is a parallelogram as opposite sides are parallel.
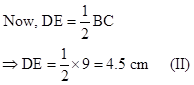
Also, in ΔABC, E is the mid-point of AC and ![]() .
.
Then, by converse of Mid-point theorem, F is the mid-point of BC.
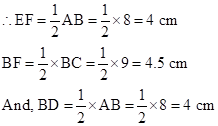
Therefore, the perimeter of quadrilateral BDEF
= BD + DE + EF + BF
= (4 + 4.5 + 4 + 4.5) cm
= 17 cm
Solution 2
Given: P, Q and R are mid-points of sides AB, BC and CD respectively of a rhombus ABCD.
To prove: PQ ⊥ QR
Construction: Draw diagonals AC and BD.
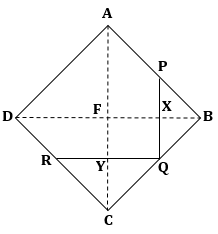
In ΔABC, P and Q are mid-points of the sides AB and BC respectively.
Then, by Mid-point theorem,
![]()
![]()
In ΔBCD, Q and R are mid-points of the sides BC and CD respectively.
Then, by Mid-point theorem,
![]()
![]()
Hence, FXQY is a parallelogram as opposite sides are parallel.
In parallelogram FXQY,
∠YFX = 90o (diagonals of a rhombus bisect each other at right angle)
⇒ ∠YQX = 90o (Opposite angles of a parallelogram are equal)
Hence, PQ ⊥ QR.
Solution 3
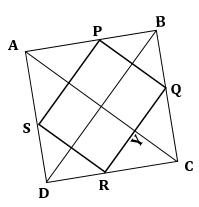
In ΔABC, P and Q are mid-points of the sides AB and BC respectively.
Then, by Mid-point theorem,
![]() (I)
(I)
In ΔADC, R and S are mid-points of the sides CD and AD respectively.
Then, by Mid-point theorem,
![]() (II)
(II)
From (I) and (II),
![]()
Similarly, ![]()
Hence, PQRS is a parallelogram as opposite sides are parallel and equal.
Now, ![]()
And, AC ⊥ BD
⇒ PQ ⊥ BD
So, PQRS is a rectangle.
Hence, the quadrilateral obtained by joining the mid-points of its adjacent sides is a rectangle.
Solution 4
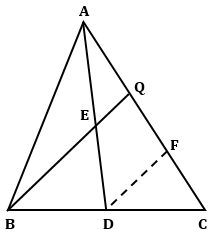
Construction: Draw ![]()
In ΔCBQ, D is the mid-point of BC and ![]() .
.
Then, by converse of Mid-point theorem,
F is the mid-point of CQ.
∴ 2DF = BQ
In ΔADF, E is the mid-point of AD and ![]() .
.
Then, by converse of Mid-point theorem,
Q is the mid-point of AF.
∴ 2EQ = DF
Now,
Solution 5

Solution 6
The figure is shown below
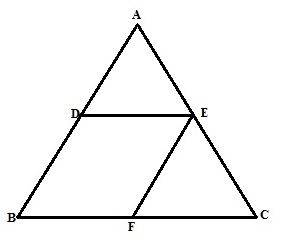
From figure since E is the midpoint of AC and EF||AB
Therefore F is the midpoint of BC and 2DE=BC or DE=BF
Again D and E are midpoint ,therefore DE||BF and EF=BD
Hence BDEF is a parallelogram.
Now
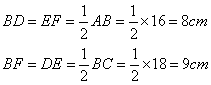
Therefore perimeter of BDEF=2(BF+EF)=![]()
Solution 7
Given AD and CE are medians and DF || CE.
We know that from the midpoint theorem, if two lines are parallel and the starting point of segment is at the midpoint on one side, then the other point meets at the midpoint of the other side.
Consider triangle BEC. Given DF || CE and D is midpoint of BC. So F must be the midpoint of BE.
![]()
Substitute value of BE in first equation, we get
![]()
Hence Proved
Solution 8
Given ABCD is parallelogram, so AD = BC, AB = CD.
Consider triangle APB, given EC is parallel to AP and E is midpoint of side AB. So by midpoint theorem, C has to be the midpoint of BP.
So BP = 2BC, but BC = AD as ABCD is a parallelogram.
Hence BP = 2AD
Consider triangle APB, AB || OC as ABCD is a parallelogram. So by midpoint theorem, O has to be the midpoint of AP.
Hence Proved
Solution 9
Consider trapezium ABCD.
Given E and F are midpoints on sides AD and BC, respectively.
_SHR_files/20141020120110_image009.jpg)
We know that AB = GH = IJ
From midpoint theorem, ![]()
Consider LHS,
AB + CD = AB + CJ + JI + ID = AB + 2HF + AB + 2EG
So AB + CD = 2(AB + HF + EG) = 2(EG + GH + HF) = 2EF
AB + CD = 2EF
Hence Proved
Solution 10
Given Δ ABC
AD is the median. So D is the midpoint of side BC.
Given DE || AB. By the midpoint theorem, E has to be midpoint of AC.
So line joining the vertex and midpoint of the opposite side is always known as median. So BE is also median of Δ ABC.
Solution 11
If adjacent sides of a parallelogram are equal, then it is rhombus.
Now, the diagonals of a rhombus bisect each other and are perpendicular to each other.
Let the lengths of the diagonals be x and y.
Diagonal of length y be equal to the sides of rhombus.
Thus, each side of rhombus = y
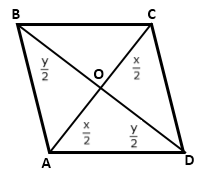
Now, in right-angles ΔBOC, by Pythagoras theorem
OB2 + OC2 = BC2