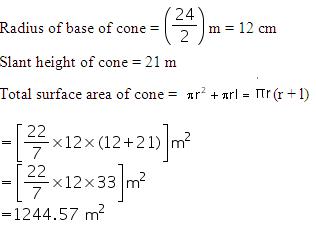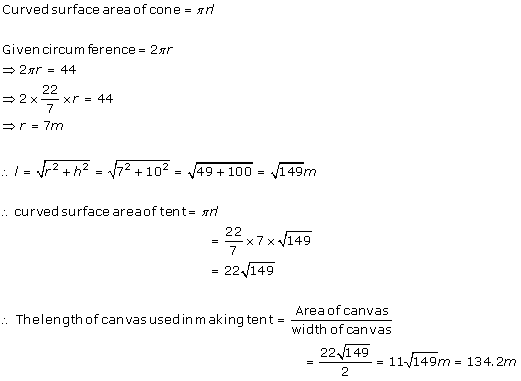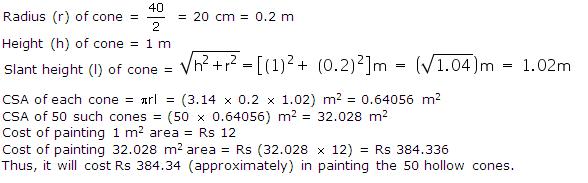Class 9 RD SHARMA Solutions Maths Chapter 20: Surface Areas and Volume of A Right Circular Cone
Ex. 20.1
Ex. 20.2
20.24
20.25
Surface Areas and Volume of A Right Circular Cone Exercise Ex. 20.1
Solution 1
Solution 2
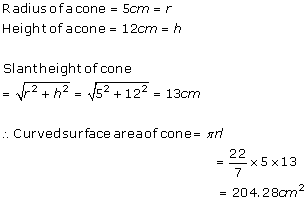
Solution 3
Solution 4
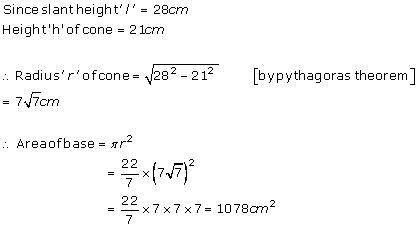
Solution 5
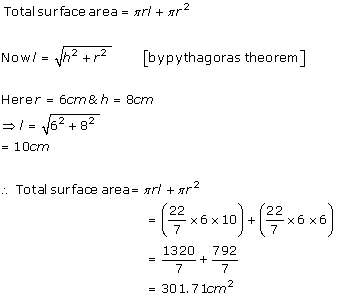
Solution 6
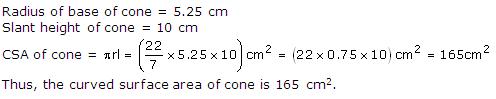
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
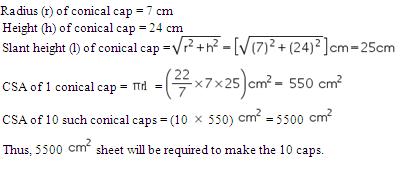
Solution 12
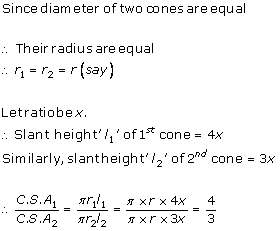
Solution 13
Solution 14
Solution 15
(i) Slant height of cone = 14 cm
Let radius of circular end of cone be r.
CSA of cone =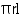
Let radius of circular end of cone be r.
CSA of cone =
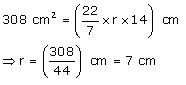
Thus, the radius of circular end of the cone is 7 cm.
(ii) Total surface area of cone = CSA of cone + Area of base
=
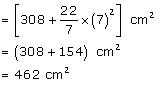
Thus, the total surface area of the cone is 462 
.
.Solution 16
Solution 17
Solution 18
Solution 19
Height (h) of conical tent = 8 m
Radius (r) of base of tent = 6 m
Slant height (l) of tent =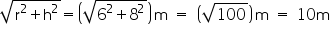
CSA of conical tent =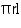
= (3.14 
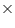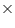6 10) 
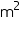= 188.4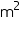
Let length of tarpaulin sheet required be L.
As 20 cm will be wasted so, effective length will be (L - 0.2 m)
Breadth of tarpaulin = 3 m
Area of sheet = CSA of tent
[(L - 0.2 m)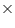 3] m = 188.4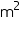
L - 0.2 m = 62.8 m
L = 63 m
Thus, the length of the tarpaulin sheet will be 63 m.
Radius (r) of base of tent = 6 m
Slant height (l) of tent =
CSA of conical tent =
= (3.14 6 10) = 188.4 Let length of tarpaulin sheet required be L.
As 20 cm will be wasted so, effective length will be (L - 0.2 m)
Breadth of tarpaulin = 3 m
Area of sheet = CSA of tent
[(L - 0.2 m)
3] m = 188.4 L - 0.2 m = 62.8 m
L = 63 m
Thus, the length of the tarpaulin sheet will be 63 m.
Solution 20
Solution 21
Solution 22
Solution 23
Surface Areas and Volume of A Right Circular Cone Exercise Ex. 20.2
Solution 1
(i) Radius (r) of cone = 6 cm
Height (h) of cone = 7 cm
Volume of cone
(ii) Radius (r) of cone = 3.5 cm
Height (h) of cone = 12 cm
Volume of cone
(iii)
Height (h) of cone = 7 cm
Volume of cone
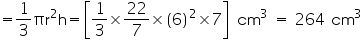
(ii) Radius (r) of cone = 3.5 cm
Height (h) of cone = 12 cm
Volume of cone
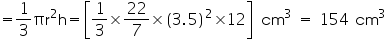
(iii)
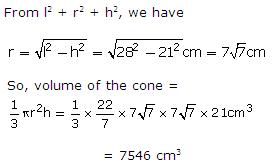
Solution 2
(i) Radius (r) of cone = 7 cm
Slant height (l) of cone = 25 cm
Height (h) of cone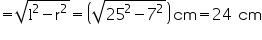
Volume of cone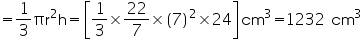
Capacity of the conical vessel =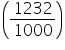
litres= 1.232 litres
Slant height (l) of cone = 25 cm
Height (h) of cone
Volume of cone
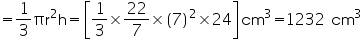
Capacity of the conical vessel =
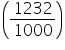litres= 1.232 litres(ii) Height (h) of cone = 12 cm
Slant height (l) of cone = 13 cm
Slant height (l) of cone = 13 cm
Radius (r) of cone
Volume of cone
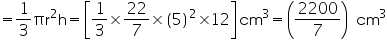= 314.28 cm3Capacity of the conical vessel =
litres = 
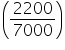litres.Solution 3
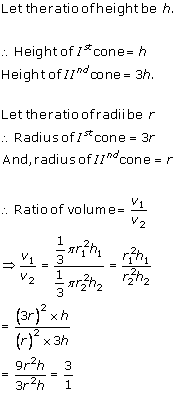
Solution 4
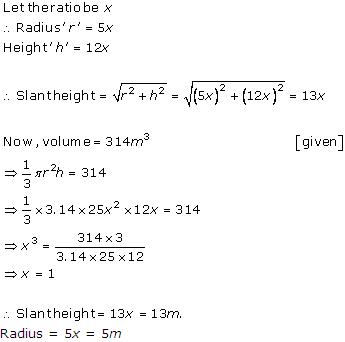
Solution 5
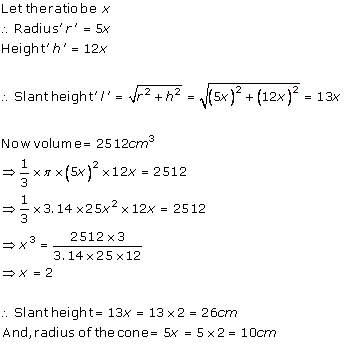
Solution 6
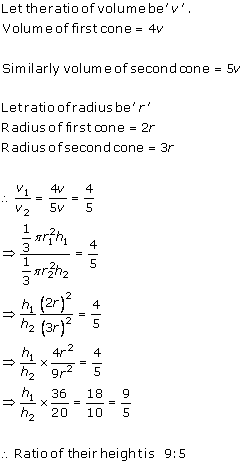
Solution 7
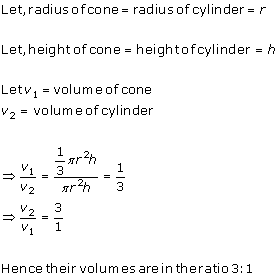
Solution 8
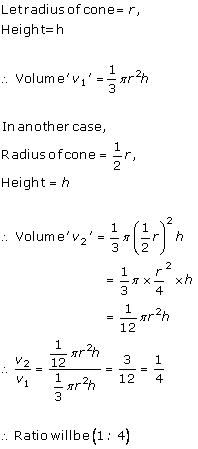
Solution 9
Solution 10
Solution 11
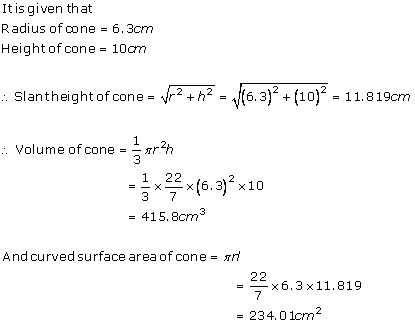
Solution 12
Solution 13
(i) Radius of cone = 
=14 cm
Let height of cone be h.
Volume of cone = 9856 cm3
=14 cmLet height of cone be h.
Volume of cone = 9856 cm3
h = 48 cm
Thus, the height of the cone is 48 cm.
(ii) Slant height (l) of cone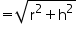 
Thus, the slant height of the cone is 50 cm.
(iii) CSA of cone =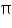 
rl = 
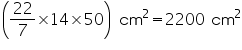
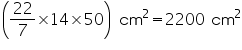
rl = Solution 14
Radius (r) of pit =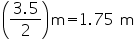
Depth (h) of pit = 12 m
Volume of pit =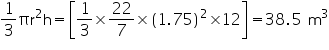
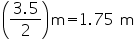
Depth (h) of pit = 12 m
Volume of pit =
Capacity of the pit = (38.5 
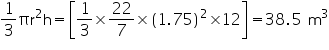
1) kilolitres = 38.5 kilolitresSolution 15
Surface Areas and Volume of A Right Circular Cone Exercise 20.24
Solution 1
A cone has two surfaces as follows: one curved surface and another bottom surface.
Hence, correct option is (b).
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
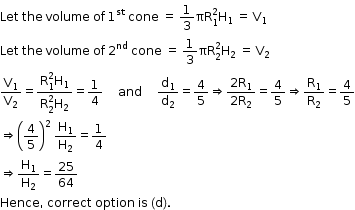
Solution 7
Surface Areas and Volume of A Right Circular Cone Exercise 20.25
Solution 8
Solution 9
Solution 10
Solution 13
Solution 14
Solution 11
Solution 12
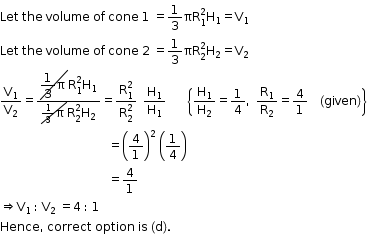
Solution 15
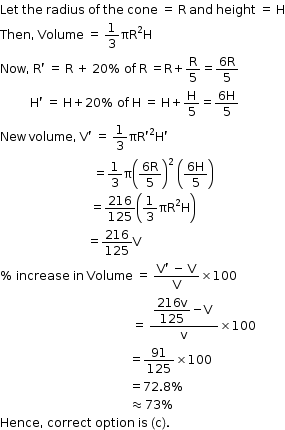
Solution 16
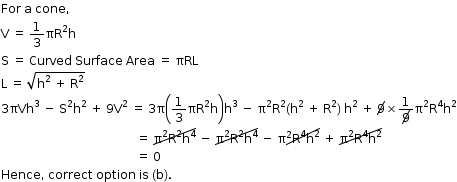
Solution 17
