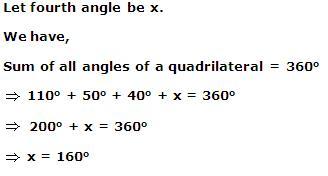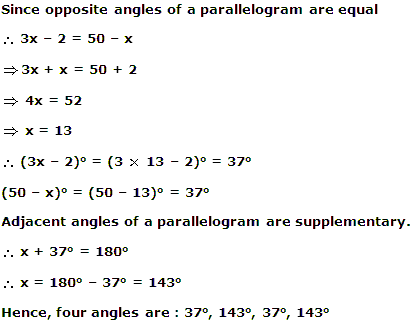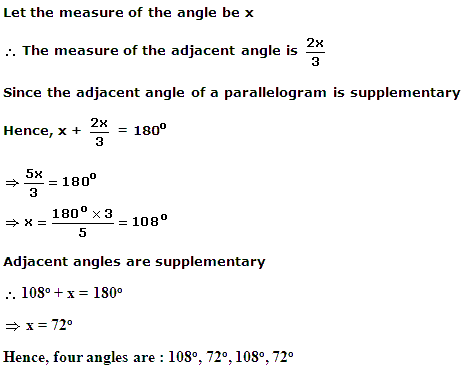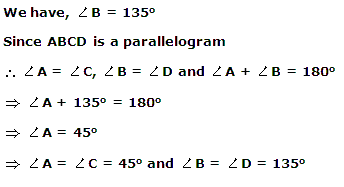Class 9 RD SHARMA Solutions Maths Chapter 13 - Quadrilaterals
Solutions are a valuable educational resource as they help students easily navigate their academic journey confidently. They provide a deeper understanding of the subject during self-study and enhance the learning outcomes. Mathematics is considered one of the most essential subjects as it plays an important role in science, business, and technology fields.
RD Sharma Solutions for CBSE Mathematics is a highly regarded resource. It provides comprehensive and detailed explanations for all the questions in the textbook. Breaking down larger concepts into manageable steps, these solutions not only provide better clarity but also improve the problem-solving skills of students. This comes in especially useful when solving complex or tricky questions.
One of the most important chapters covered in CBSE Class 9 Math is Quadrilaterals. In this resource, you can gain an in-depth understanding and step-by-step solutions to the problems related to this geometric shape.
Quadrilaterals are polygons that have four sides and four angles. The CBSE Class 9 Mathematics curriculum teaches students about the various types of quadrilaterals, such as parallelograms, rectangles, squares, rhombuses, trapeziums, and kites. Students learn the properties and characteristics of these quadrilaterals and solve related problems. With access to detailed explanations and examples in the RD Sharma solution, students gain a solid understanding of the unique features of each type of quadrilateral.
As one of the most popular online education platforms in the country, Topper Learning aims to make online education affordable and accessible to all students. They can benefit from advanced and extensive resources such as textbook solutions which are free of cost, sample papers and MCQ questions to practise what they have already learned, etc. Students can watch video lessons or check out important questions to ensure regular practice and improved subject results.
Quadrilaterals Exercise Ex. 13.1
Solution 1
Solution 2

Solution 3
Since the sum of all interior angles of a quadrilateral is 360o.
30x = 360o
x = 12o
Hence, the angles are
3x = 3
5x = 5
9x = 9
13x = 13
Solution 4

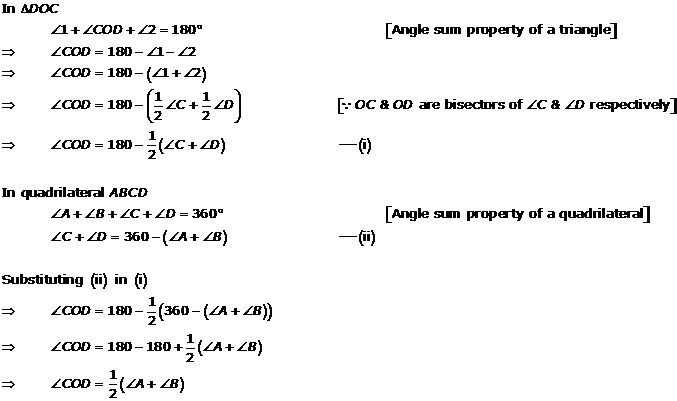
Quadrilaterals Exercise Ex. 13.2
Solution 1
Solution 2
Solution 3
Solution 4
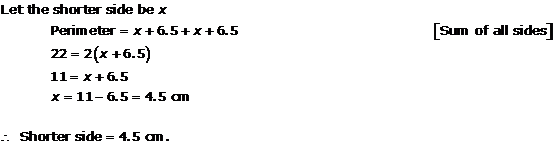
Solution 5
Solution 6
Solution 7
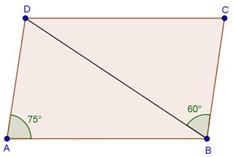
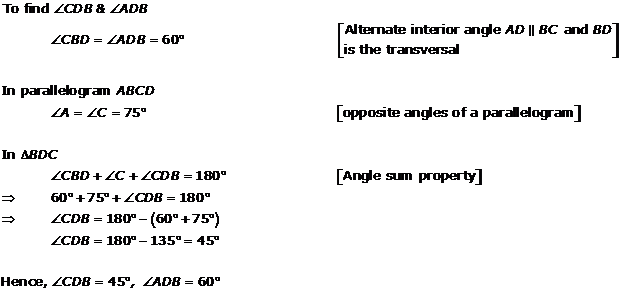
Solution 8
i. F
ii. T
iii. F
iv. F
v. T
vi. F
vii. F
viii. T
Solution 9
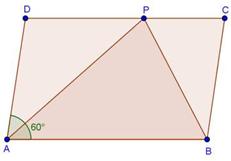
Solution 10
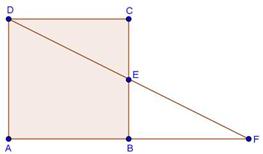
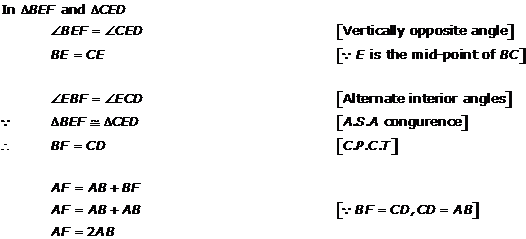
Quadrilaterals Exercise Ex. 13.3
Solution 1
C and
D are cosecutive interior angles on the same side of the transversal CD. Therefore,
C +
D = 180o
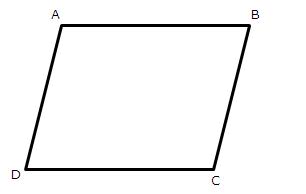
Solution 2
Solution 3
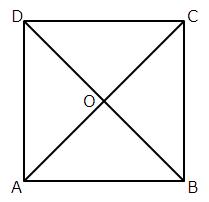
Since, diagonals of a square bisect each other at right angle. Therefore, ![]() AOB = 90o
AOB = 90o
Solution 4
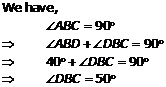
Solution 5
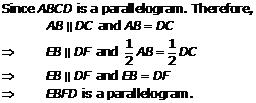
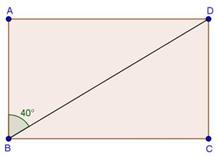
Solution 6

Solution 7
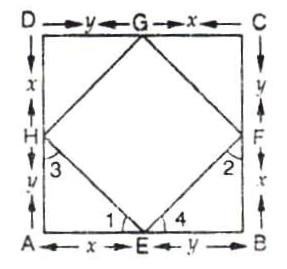
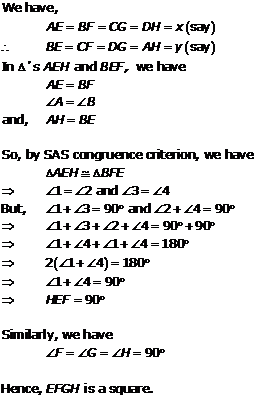
Solution 8
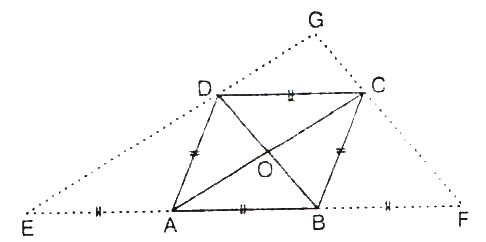

Solution 9
Quadrilaterals Exercise Ex. 13.4
Solution 1
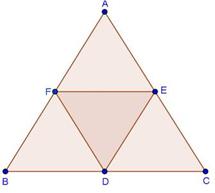

Solution 2

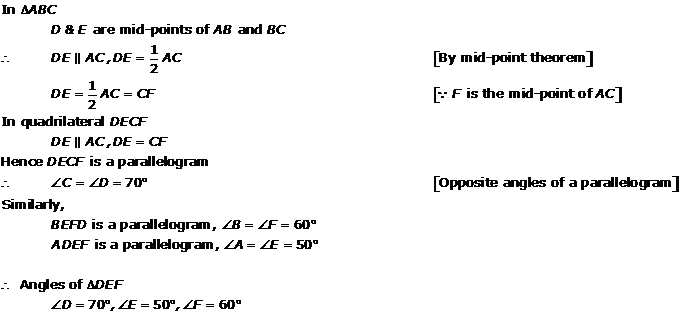
Solution 3
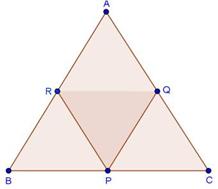
Solution 4
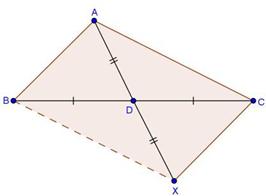
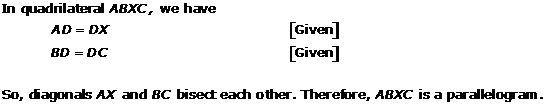
Solution 5
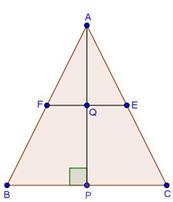

Solution 6
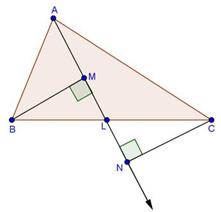
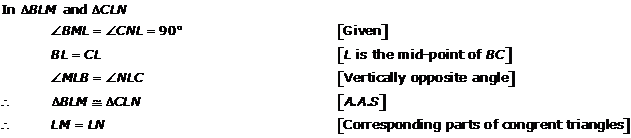
Solution 7
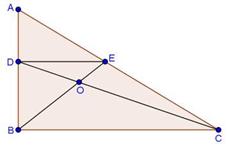
Solution 8
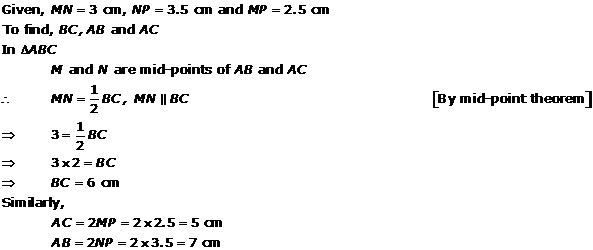
Solution 9


Solution 10

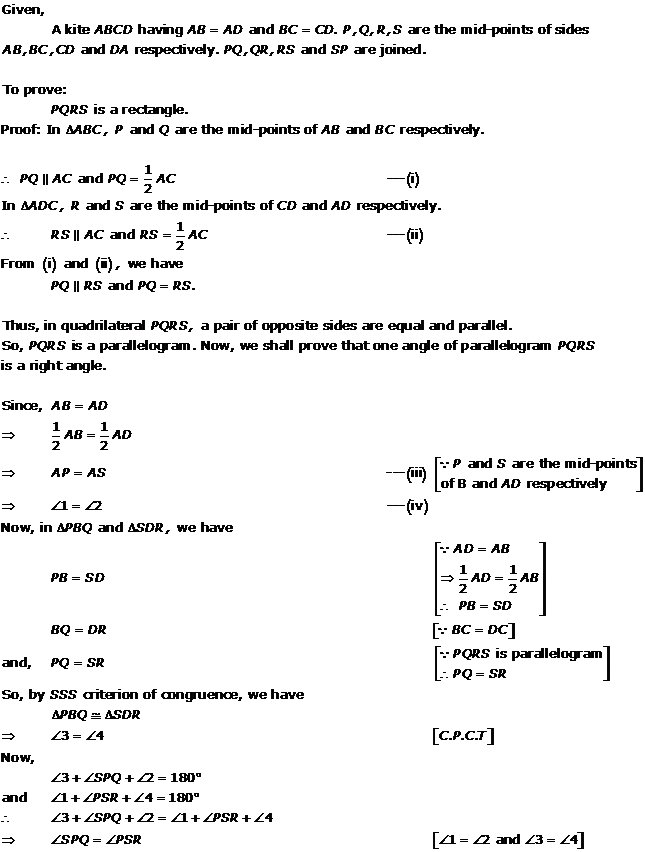
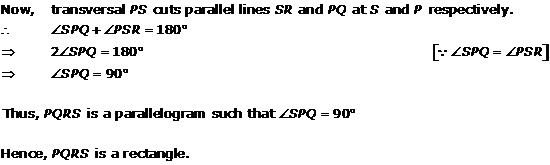
Solution 11

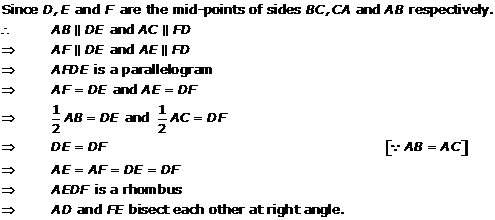
Solution 12
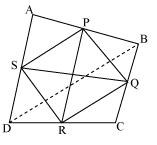
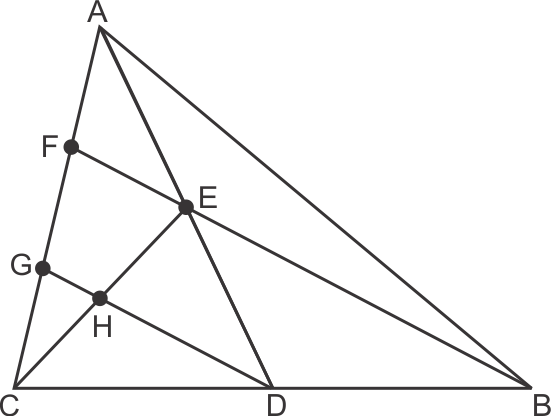
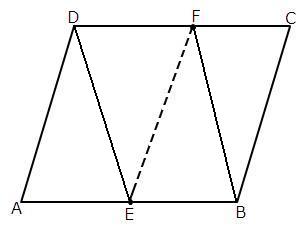
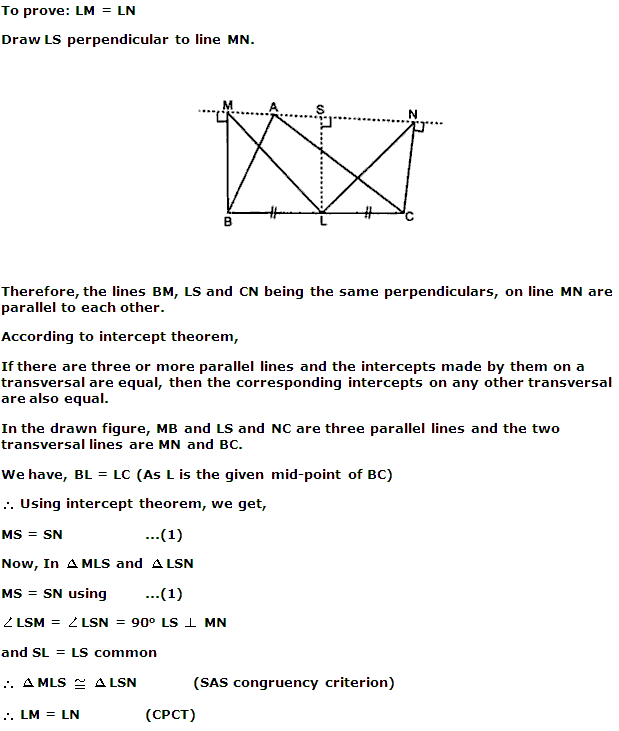
Join PQ, QR, RS, SP and BD.
In
So, By using mid-point theorem, we can say that
SP || BD and SP =
Similarly in
QR || BD and QR =
From equations (1) and (2), we have
SP || QR and SP = QR
As in quadrilateral SPQR one pair of opposite sides are equal and parallel to
each other.
So, SPQR is a parallelogram.
Hence, PR and QS bisect each other.
Solution 13
(i) isosceles
(ii) right triangle
(iii) parallelogram
Solution 14
Solution 15

Solution 16
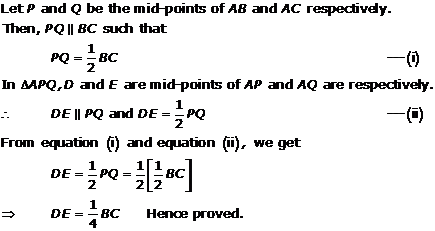
Solution 17
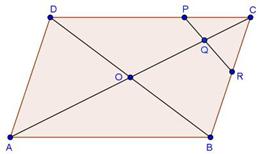
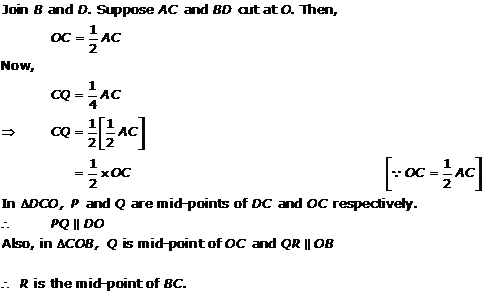
Solution 18
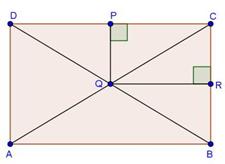
Solution 19
Solution 20
Quadrilaterals Exercise 13.70
Solution 1

ABCD is a Quadrilateral.
The opposite sides AB and DC, AD and BC have no common point.
Hence, correct option is (a).
Solution 2

Consecutive sides of a Quadrilateral ABCD are
AB and BC,
BC and CD,
CD and AD,
AD and AB,
which have only one point in common
i.e the joint point of their ends.
Hence, correct option is (b).
Quadrilaterals Exercise 13.71
Solution 3
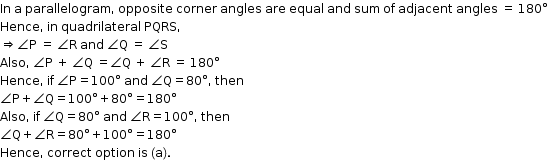
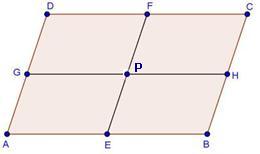
Solution 4
For a rhombus, the angle between the diagonals is 90° and not 60°.
Hence, correct option is (d).
Solution 5
Diagonals necessarily bisect opposite angles in a square.
Hence, correct option is (d).
Solution 6
The two diagonals are equal in a rectangle (property).
Hence, correct option is (c).
Solution 7
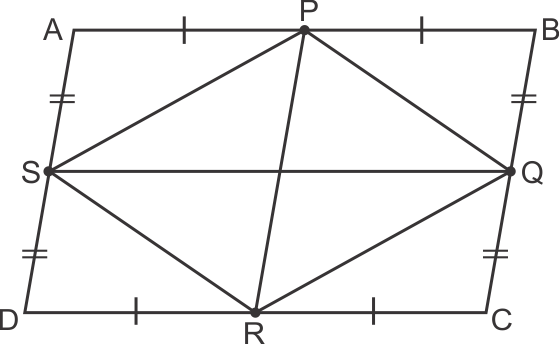


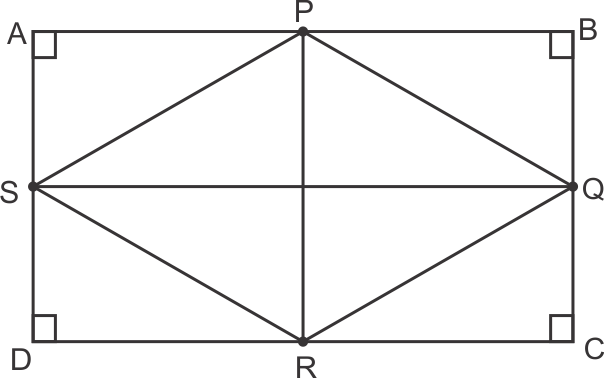

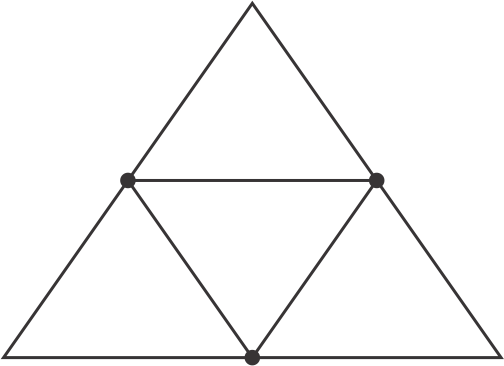

Solution 8
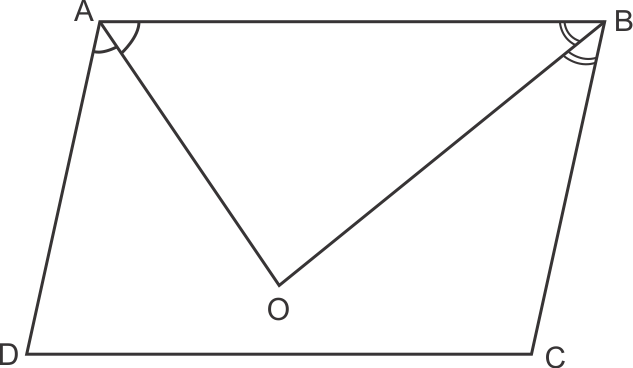

Solution 9

AR, BR, CP, DP are the bisectors of angles of parallelogram.
Because two bisectors of adjacent angles make 90° between them So PQRS is a Rectangle
Because DP and BR are acute angle bisectors so the distance between them PQ < PS (The distance between other two bisectors)
So PQ ≠ PS (So PQRS is not a square, but only a rectangle)
Hence, correct option is (c).
Solution 10


Solution 11


Solution 12
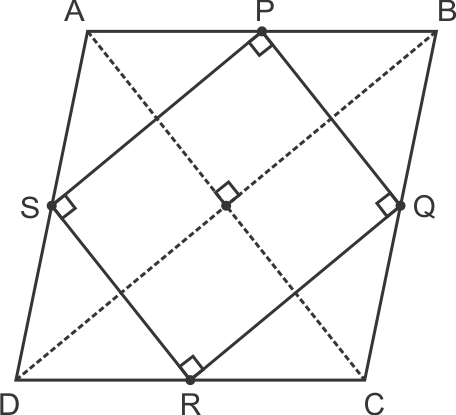

Solution 13
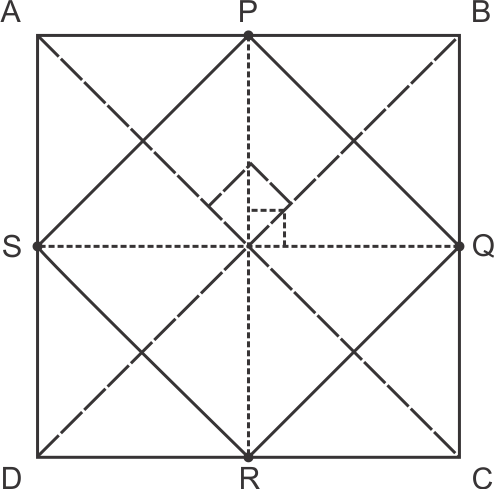

Solution 14
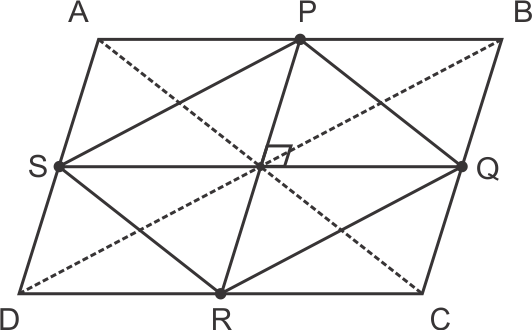

Solution 15

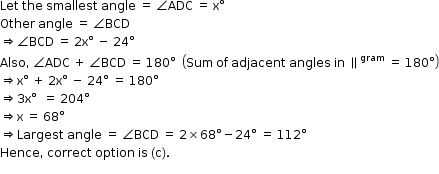
Solution 16
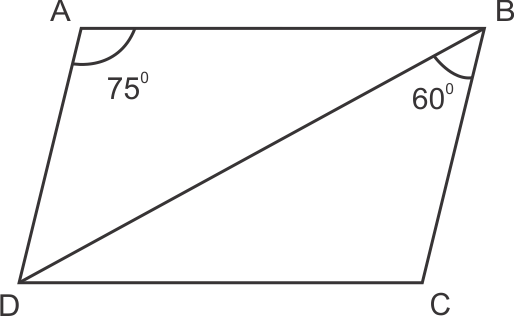

Solution 17
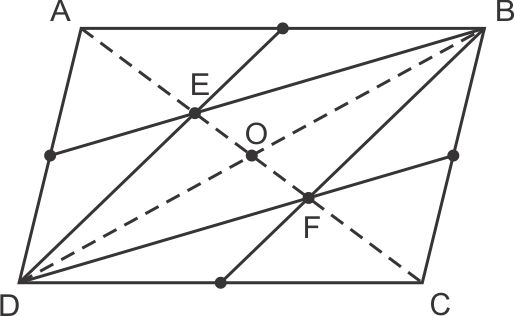

Quadrilaterals Exercise 13.73
Solution 31

Solution 32
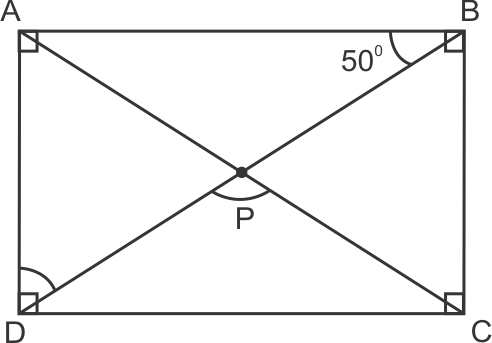

Quadrilaterals Exercise 13.72
Solution 18
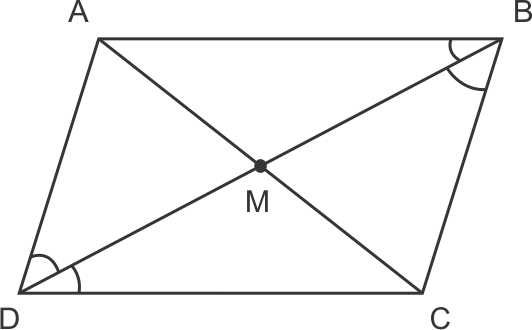

Solution 19


Solution 20
Sum of all angles of a Quadrilateral = 360°
4x + 7x + 9x + 10x = 360°
30x = 360°
x = 12°
So, sum of smallest and largest angle,
i.e. 4x + 10x = 14x = 14 × 12 = 168°
Hence, correct option is (c).
Solution 21
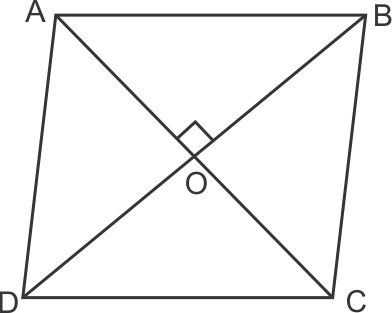

Solution 22
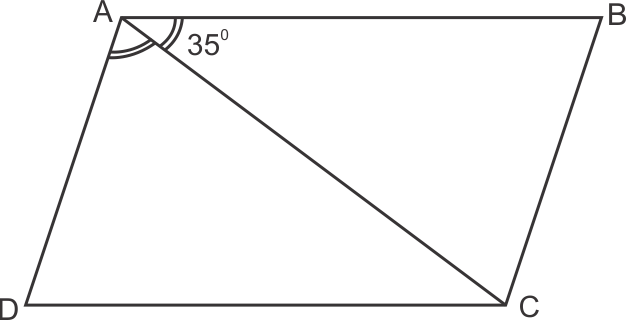
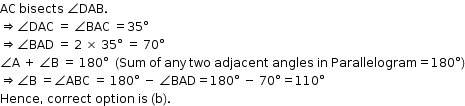
Solution 23
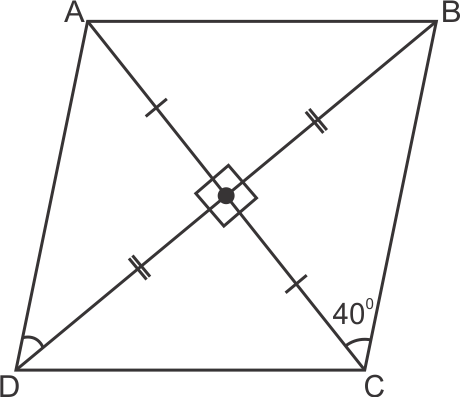

Solution 24
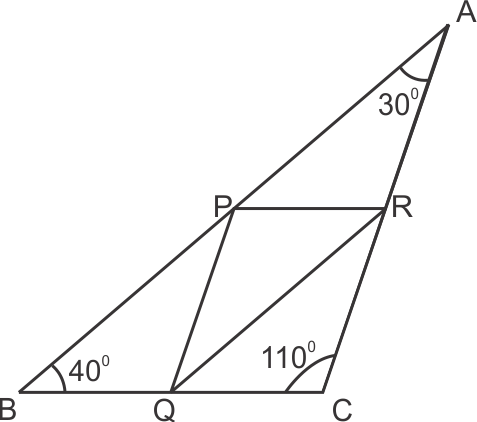

Solution 25
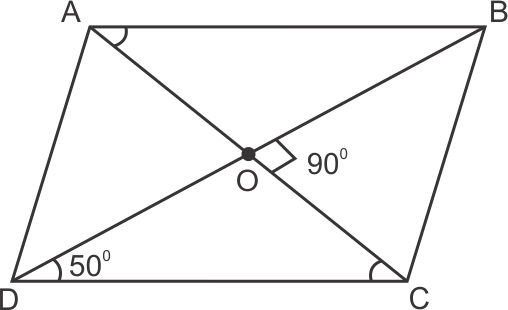

Solution 26
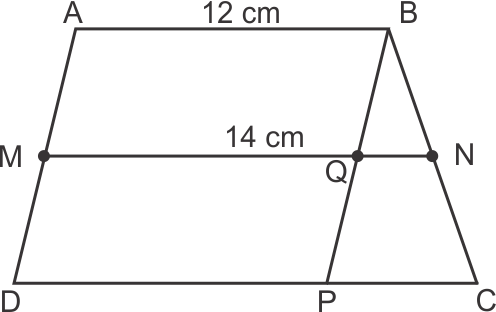

Solution 30


Solution 27
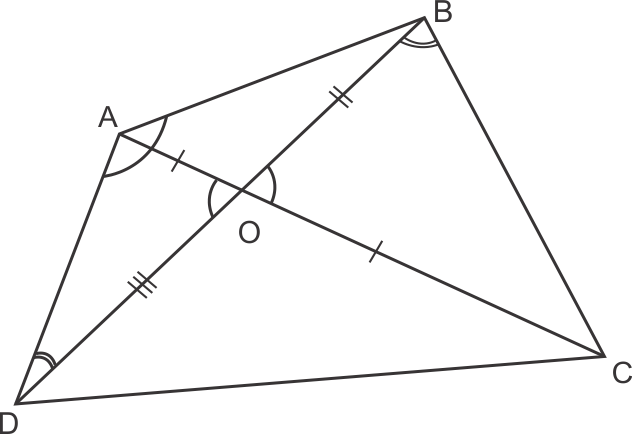

Solution 28
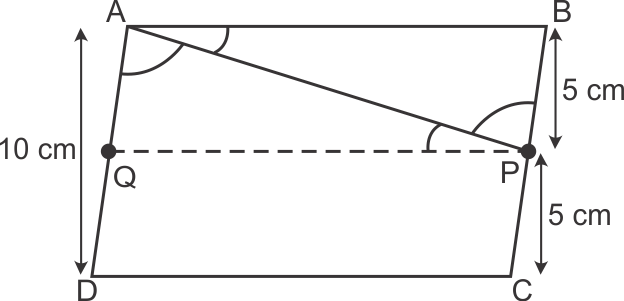

Solution 29