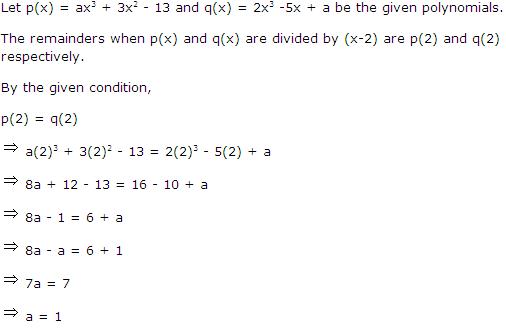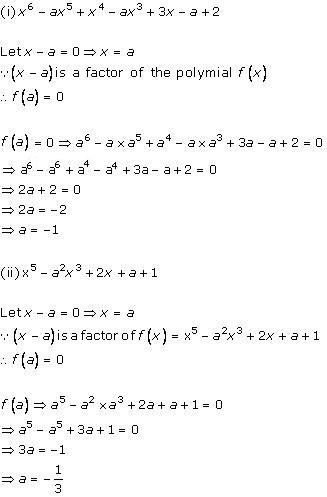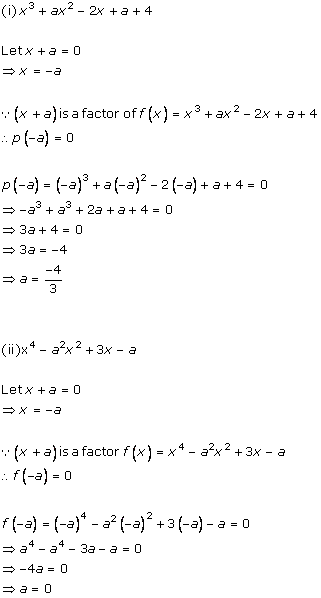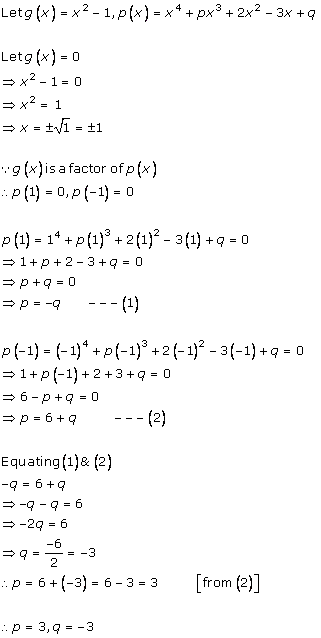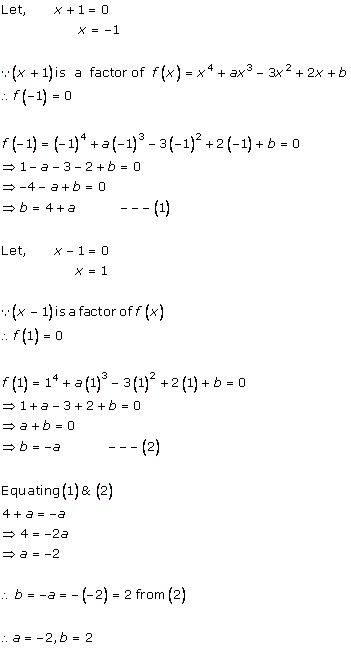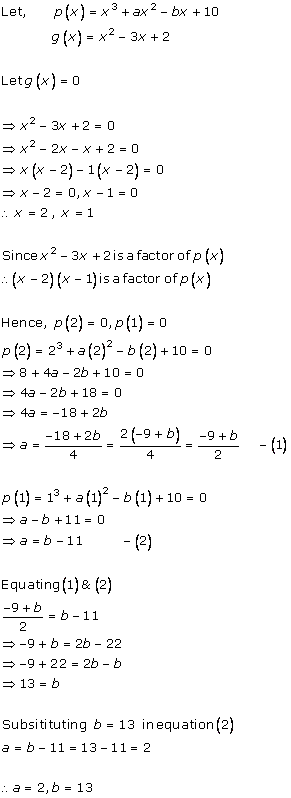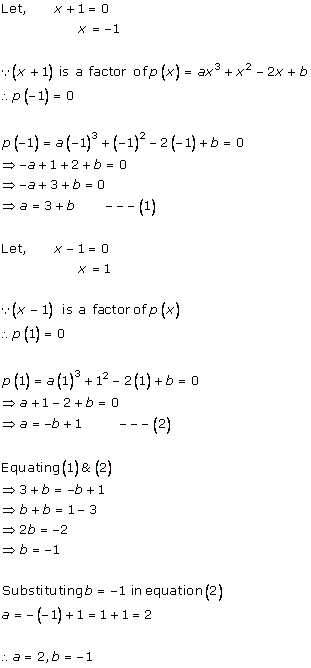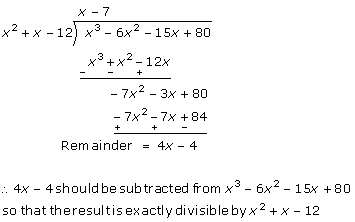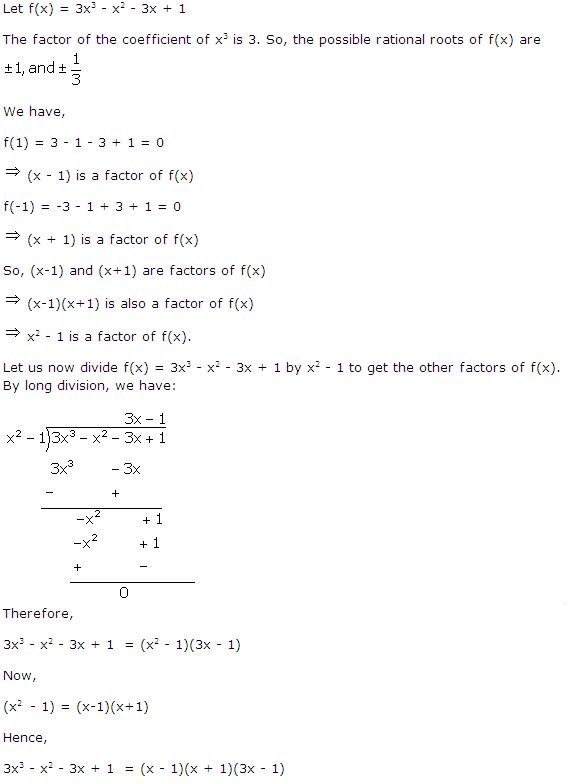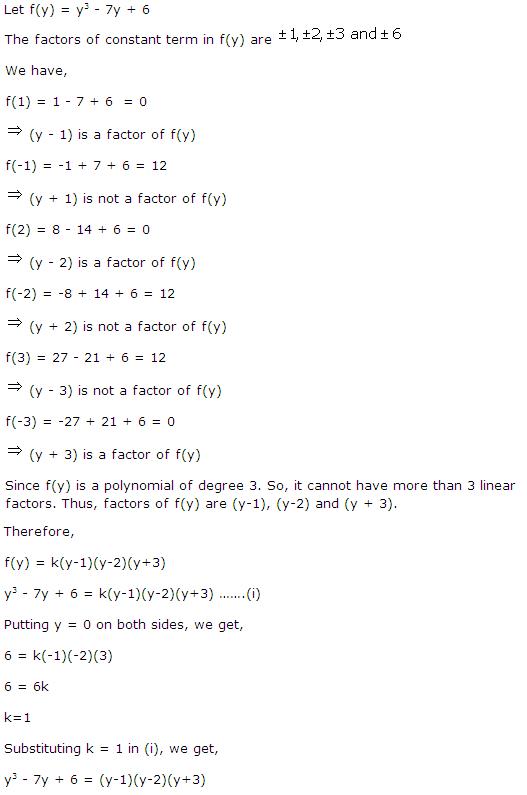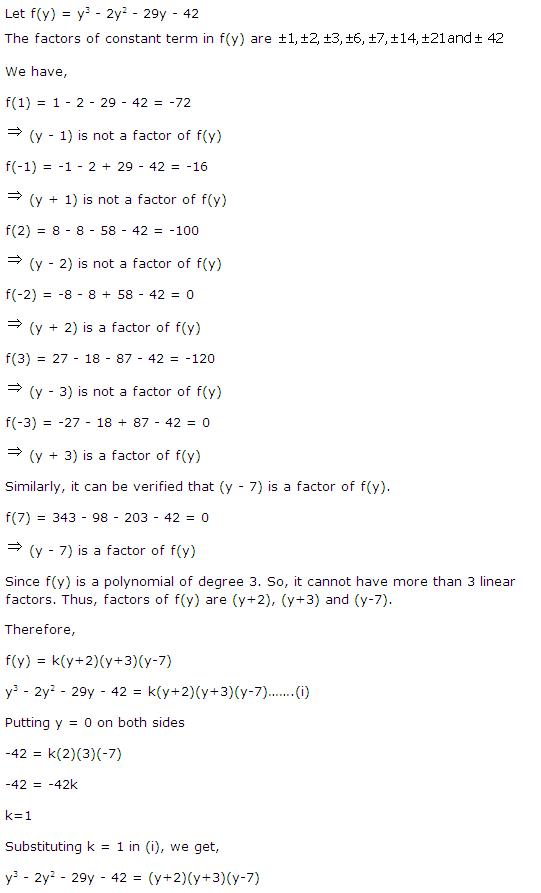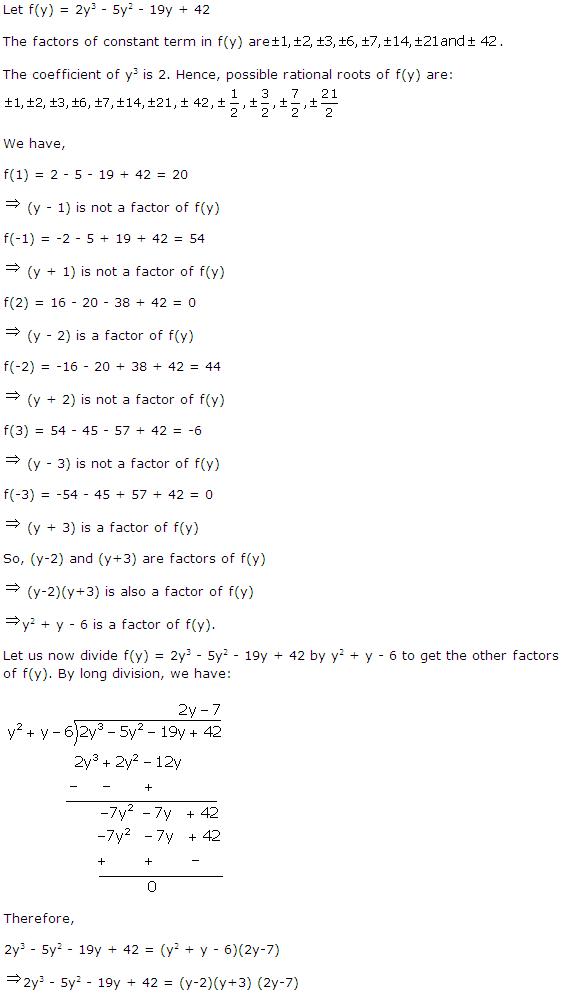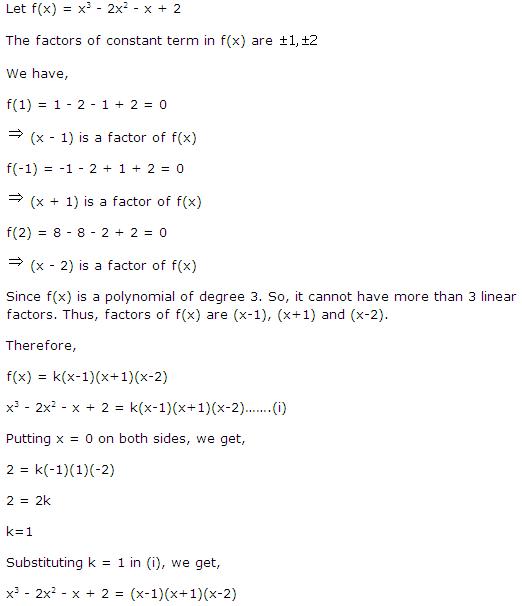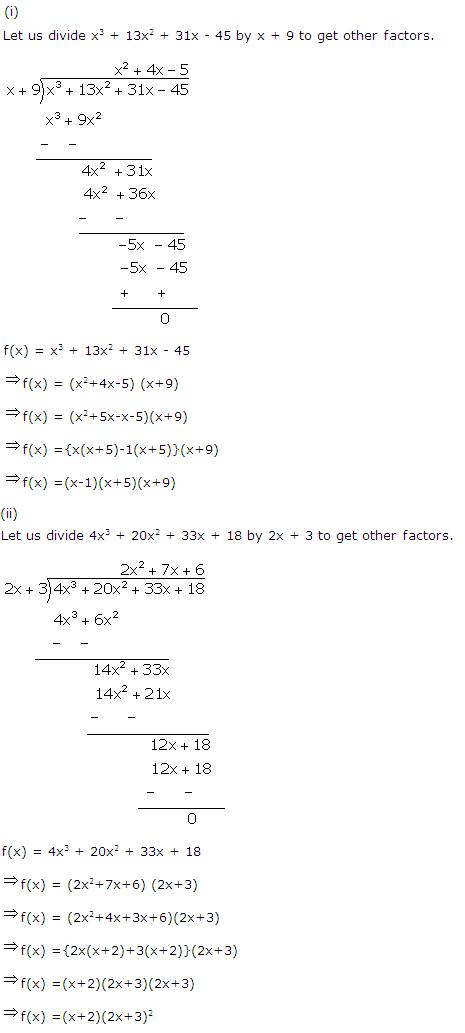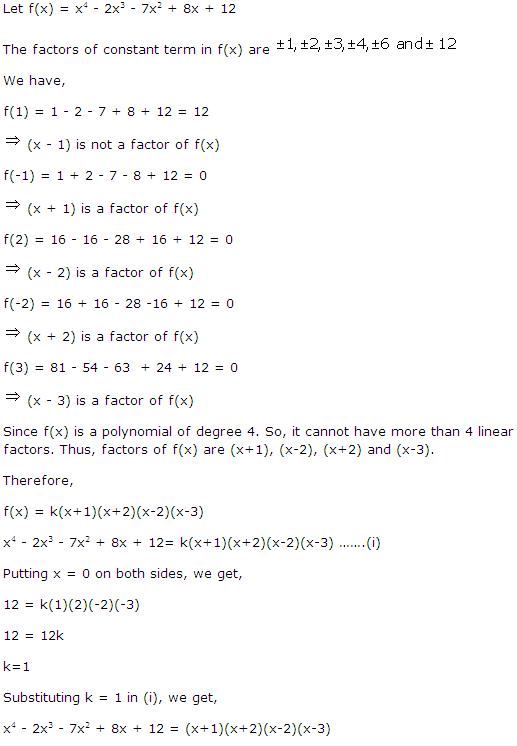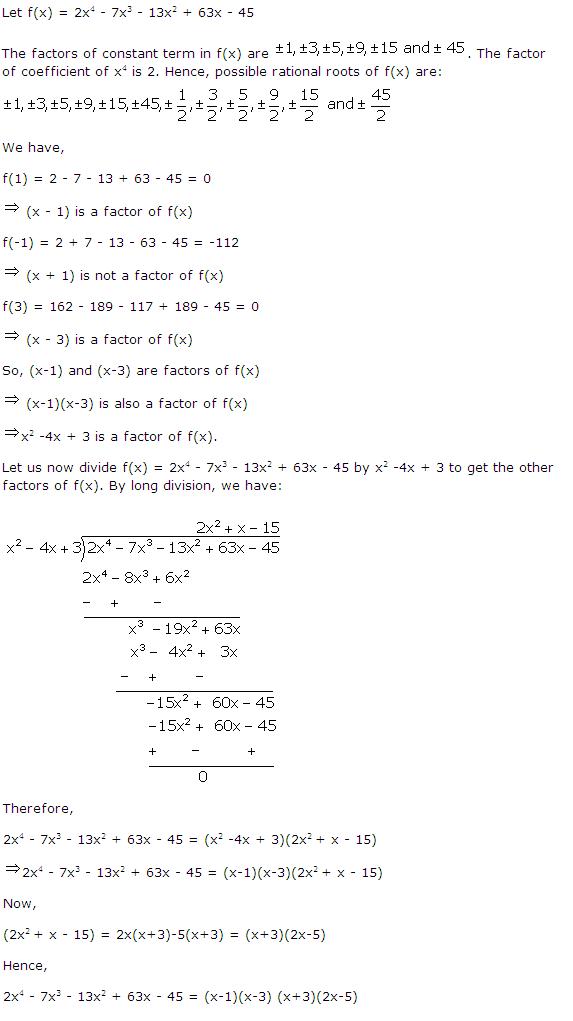Class 9 RD SHARMA Solutions Maths Chapter 6 - Factorisation of Polynomials
Factorisation of Polynomials Exercise Ex. 6.1
Solution 1

Solution 2
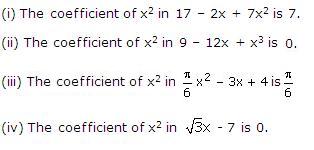
Solution 3
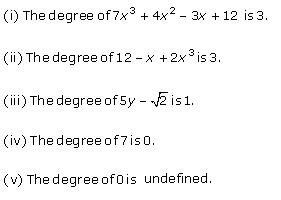
Solution 4

Solution 5

Solution 6
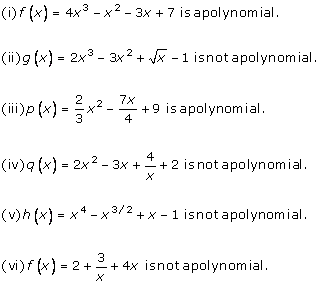
Solution 7
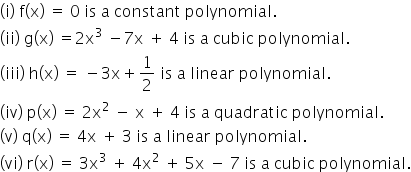
Solution 8
Binomial has two terms in it. So binomial of degree 35 can be written as x35 + 7 .
Factorisation of Polynomials Exercise Ex. 6.2
Solution 1
f(x) = 2x3 - 13x2 + 17x + 12
f(2) = 2(2)3 - 13(2)2 + 17(2) + 12
= 16 - 52 + 34 + 12
= 10
(ii)
f(-3) = 2(-3)3 - 13(-3)2 + 17(-3) + 12
= -54 - 117 - 51 + 12
= - 210
(iii)
f(0) = 2(0)3 - 13(0)2 + 17(0) + 12
= 0 - 0 + 0 + 12
=12
Solution 2

Solution 3
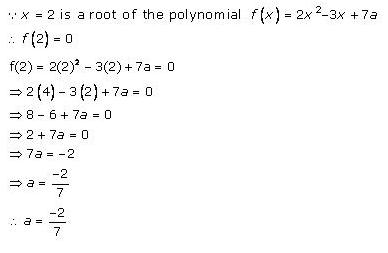
Solution 4
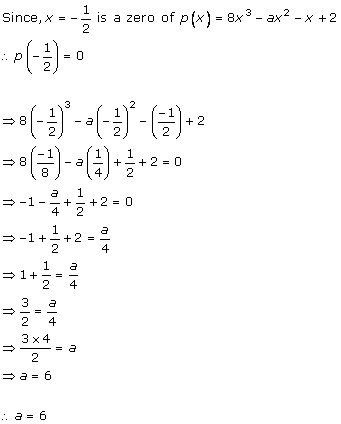
Solution 5
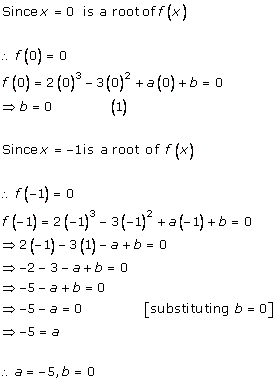
Solution 6

Solution 7
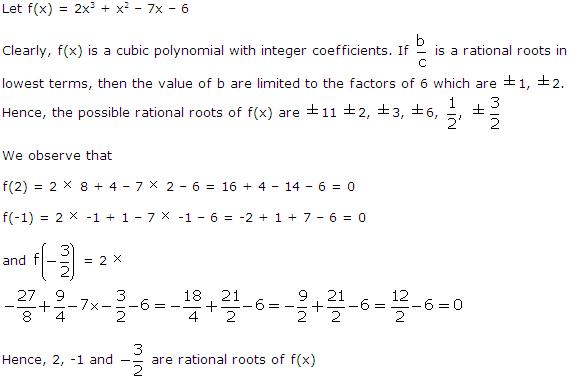
Factorisation of Polynomials Exercise Ex. 6.3
Solution 1
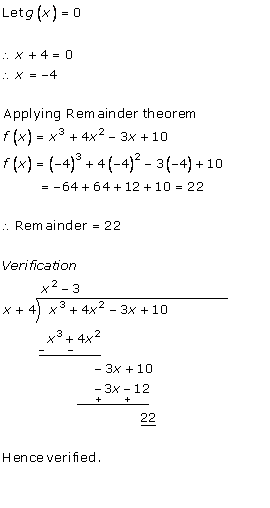
Solution 2

Solution 3
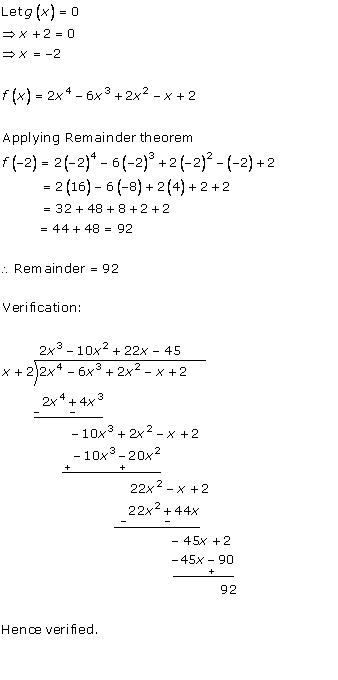
Solution 4
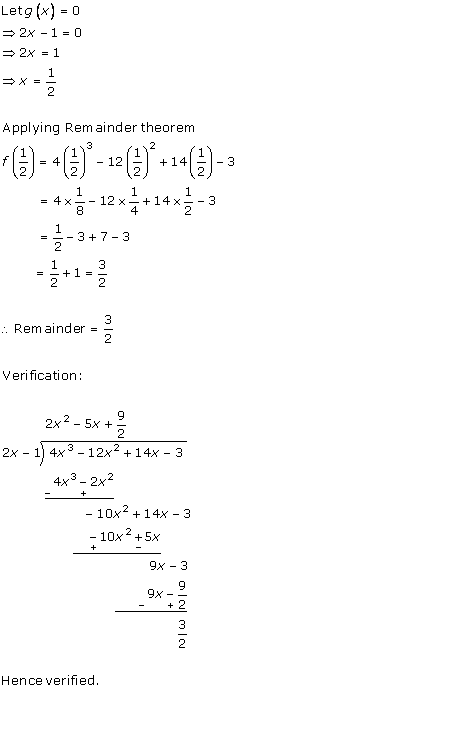
Solution 5
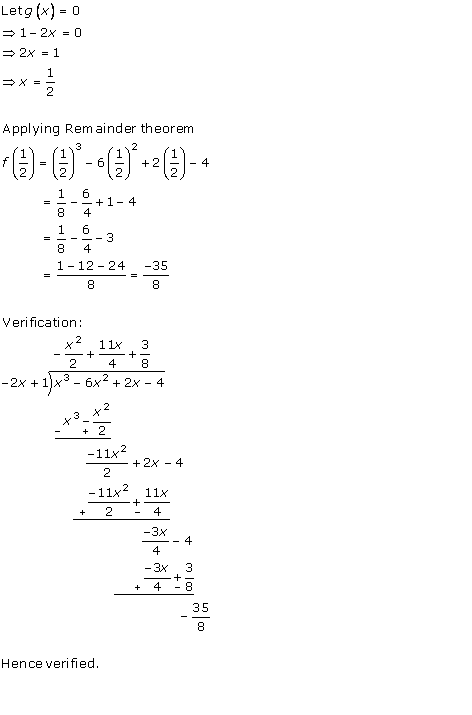
Solution 6
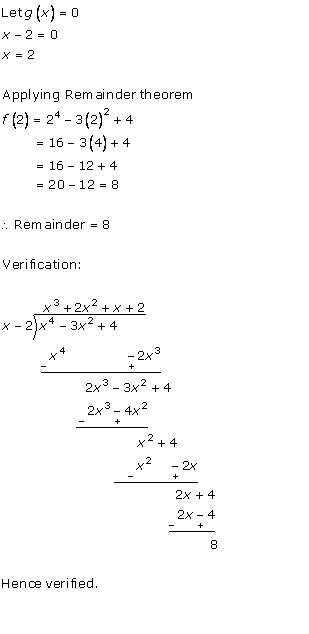
Solution 7
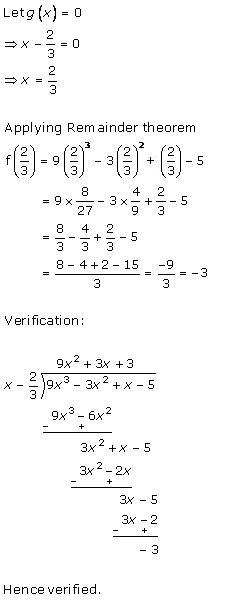
Solution 8

Solution 9
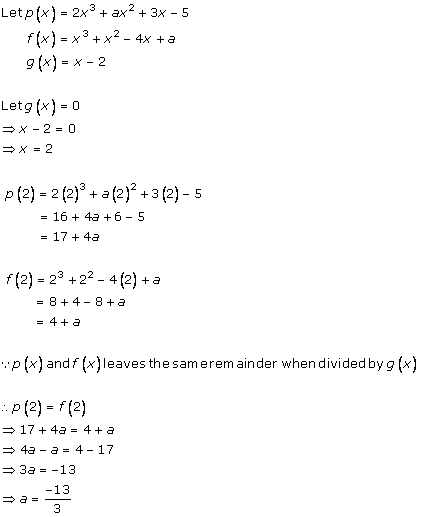
Solution 10
Solution 11
Solution 12
Factorisation of Polynomials Exercise Ex. 6.4
Solution 1

Solution 2

Solution 3
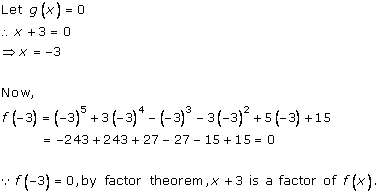
Solution 4

Solution 5
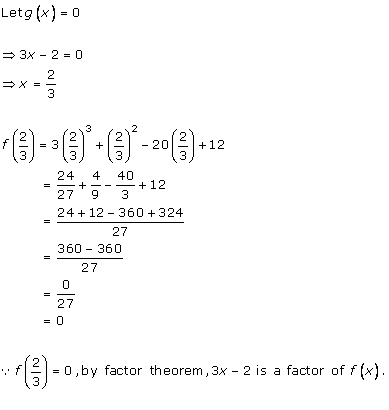
Solution 6
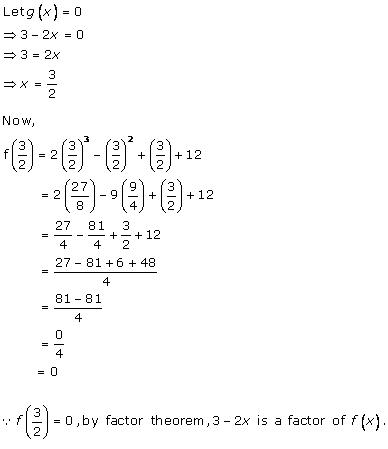
Solution 7

Solution 8
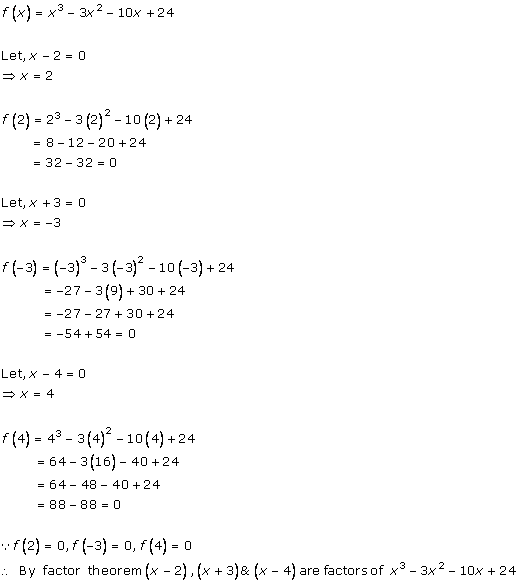
Solution 9
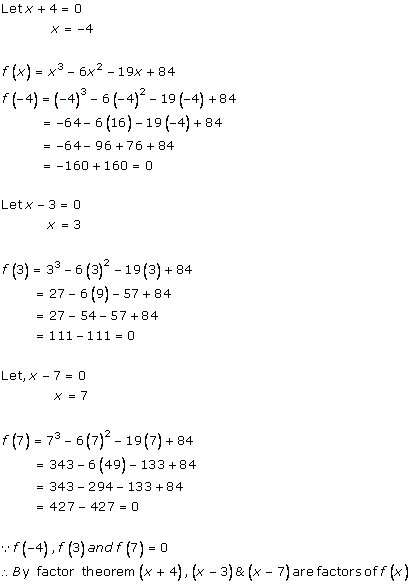
Solution 10
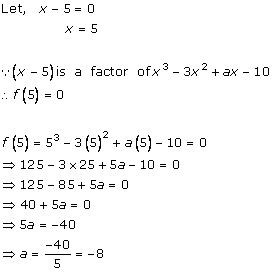
Solution 11
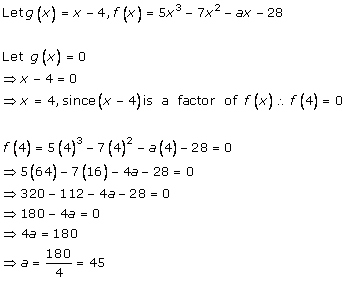
Solution 12
Solution 13
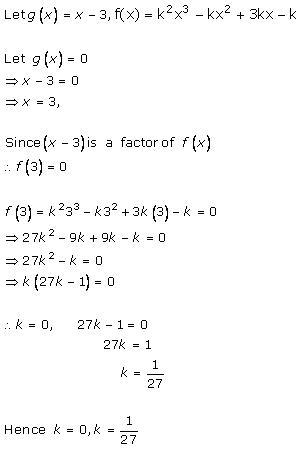
Solution 14
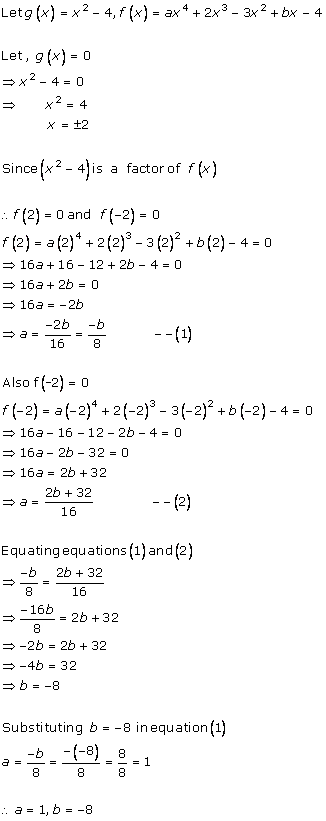
Solution 15
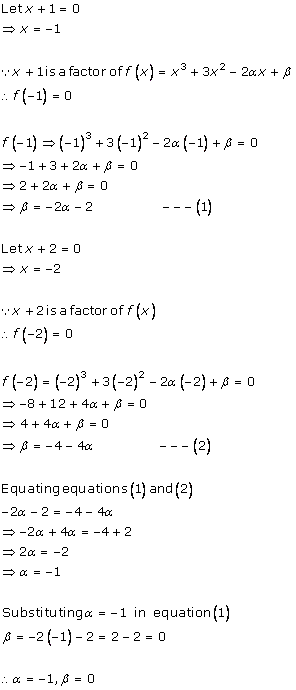
Solution 16
Solution 17
Solution 18
Solution 19
Solution 20
Solution 21
Solution 22
Solution 23
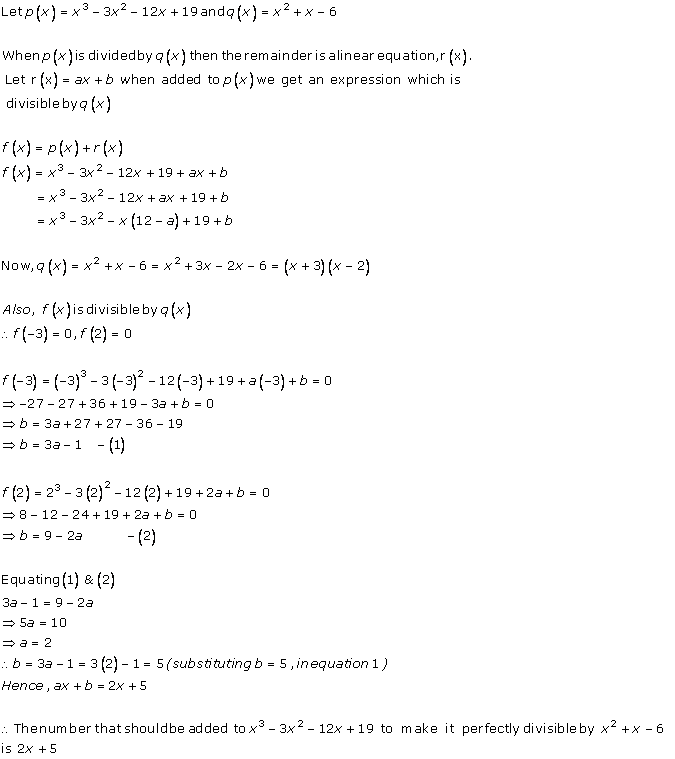
Solution 24
Solution 25
Factorisation of Polynomials Exercise Ex. 6.5
Solution 1
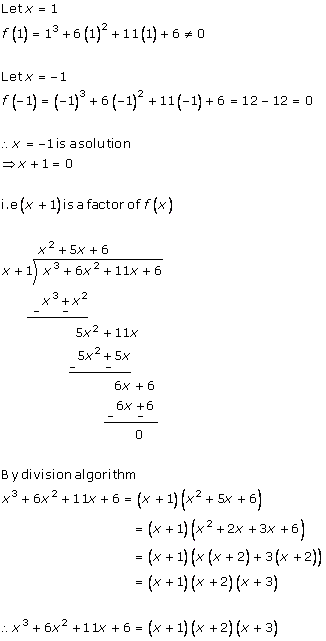
Solution 2
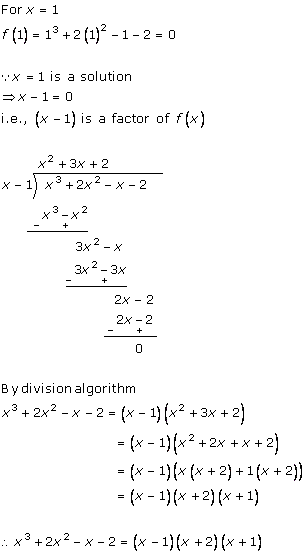
Solution 3
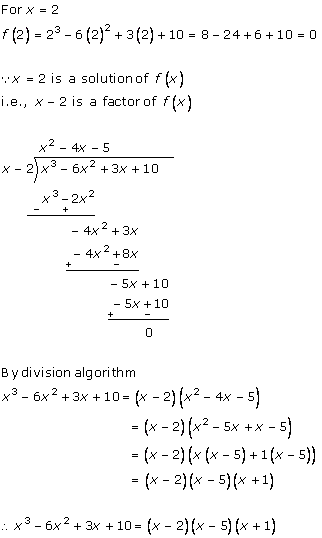
Solution 4
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Let p(x) = x3 + 13x2 + 32x + 20
The factors of 20 are ![]() 1,
1, ![]() 2,
2, ![]() 4,
4, ![]() 5 ... ...
5 ... ...
By hit and trial method
p(- 1) = (- 1)3 + 13(- 1)2 + 32(- 1) + 20
= - 1 + 13 - 32 + 20
= 33 - 33 = 0
As p(-1) is zero, so x + 1 is a factor of this polynomial p(x).
Let us find the quotient while dividing x3 + 13x2 + 32x + 20 by (x + 1)
By long division
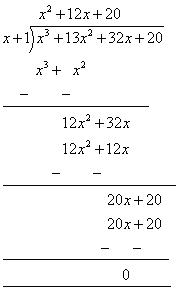
Dividend = Divisor
x3 + 13x2 + 32x + 20 = (x + 1) (x2 + 12x + 20) + 0
= (x + 1) (x2 + 10x + 2x + 20)
= (x + 1) [x (x + 10) + 2 (x + 10)]
= (x + 1) (x + 10) (x + 2)
= (x + 1) (x + 2) (x + 10)
Solution 12
Let p(x) = x3 - 3x2 - 9x - 5
Factors of 5 are ![]() 1,
1, ![]() 5.
5.
By hit and trial method
p(- 1) = (- 1)3 - 3(- 1)2 - 9(- 1) - 5
= - 1 - 3 + 9 - 5 = 0
So x + 1 is a factor of this polynomial
Let us find the quotient while dividing x3 + 3x2 - 9x - 5 by x + 1
By long division
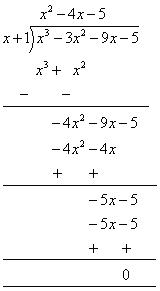
= (x + 1) (x2 - 5 x + x - 5)
= (x + 1) [(x (x - 5) +1 (x - 5)]
= (x + 1) (x - 5) (x + 1)
= (x - 5) (x + 1) (x + 1)
Solution 13
Let p(y) = 2y3 + y2 - 2y - 1
p(1) = 2 ( 1)3 + (1)2 - 2( 1) - 1
= 2 + 1 - 2 - 1= 0
So, y - 1 is a factor of this polynomial
By long division method,
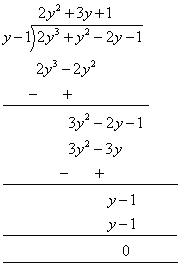
= (y - 1) (2y2 +3y + 1)
= (y - 1) (2y2 +2y + y +1)
= (y - 1) [2y (y + 1) + 1 (y + 1)]
= (y - 1) (y + 1) (2y + 1)
Solution 14
Solution 15
Solution 16
Solution 17
Solution 18
Factorisation of Polynomials Exercise 6.34
Solution 12
Let p(x) = x2 + 3ax - 2a be the given polynomial.
x - 2 is a factor of p(x).
Thus, p(2) = 0
(2)2 + 3a × 2 - 2a = 0
4 + 4a = 0
a = -1
Hence, correct option is (d).
Solution 13
Since, p(x) = x3 + 6x2 + 4x + k is exactly divisible by x + 2,
(x + 2) is a factor of p(x).
So, p(-2) = 0
i.e (-2)3 + 6(-2)2 + 4(-2) + k = 0
-8 + 24 - 8 + k = 0
24 - 16 + k = 0
8 + k = 0
k = -8
Hence, correct option is (c).
Solution 14
Let p(x) = x3 - 3x2a + 2a2x + b
(x - a) is a factor of p(x).
So, p(a) = 0
a3 - 3a2.a + 2a2.a + b = 0
a3 - 3a3 + 2a3 + b = 0
3a3 - 3a3 + b = 0
b = 0
Hence, correct option is (a).
Solution 15
Let p(x) = x140 + 2x151 + k
Since p(x) is divisible by (x + 1),
(x + 1) is a factor of p(x).
So, p(-1) = 0
(-1)140 + 2(-1)151 + k = 0
1 + 2(-1) + k = 0
1 - 2 + k = 0
k - 1 = 0
k = 1
Hence, correct option is (a).
Solution 16
If x + 2 is a factor of x2 + mx + 14,
then at x = -2,
x2 + mx + 14 = 0
i.e. (-2)2 + m(-2) + 14 = 0
4 - 2m + 14 = 0
2m = 18
m = 9
Hence, correct option is (c).
Solution 17
x - 3 is a factor of x2 - ax - 15,
then at x = 3,
x2 - ax - 15 = 0
i.e. (3)2 - a(3) - 15 = 0
9 - 3a - 15 = 0
a = -2
Hence, correct option is (a).
Solution 18
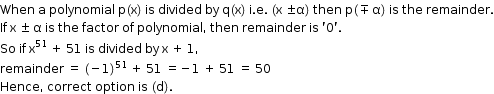
Solution 19
x + 1 is a factor of p(x) = 2x2 + kx
Then, p(-1) = 0
i.e. 2(-1)2 + k(-1) = 0
2 - k = 0
k = 2
Hence, correct option is (d).
Solution 20

Solution 21

Solution 22
If (x + 2) and (x - 1) are factors of polynomial x3 + 10x2 + mx + n,
then x = -2, x = +1 will satisfy the polynomial.
Let p(x) = x3 + 10x2 + mx + n
Then, p(-2) = 0
(-2)3 + 10(-2)2 + m(-2) + n = 0
-8 + 40 - 2m + n = 0
32 - 2m + n = 0 ....(1)
And, p(1) = 0
(1)3 + 10(1)2 + m(1) + n = 0
1 + 10 + m + n = 0
11 + m + n = 0 ....(2)
Substracting equation (1) from equation (2), we get
-21 + 3m = 0
3m = 21
m = 7
Substituting m = 7 in equation (2),
11 + 7 + n = 0
18 + n = 0
n = -18
Hence, correct option is (c).
Factorisation of Polynomials Exercise 6.35
Solution 27
If x + 1 is a factor of xn + 1,
then, at x = -1, xn + 1 = 0
(-1)n + 1 = 0
(-1)n = -1
(-1)n will be equal to -1 if and only if n is an odd integer.
If n is even, then (-1)n = 1
So, n should be an odd integer.
Hence, correct option is (a).
Solution 28
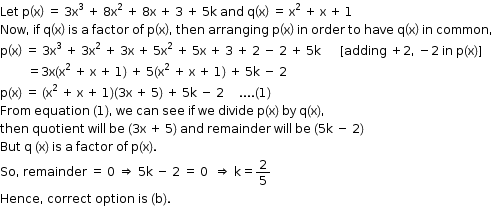
Solution 29
Correct option (c)
(3x - 1)7 = a7x7 + a6x6 + ......... + a1x + a0 ....(1)
Putting x = 1 in equation (1), we have
[3(1) - 1]7 = a7 + a6 + ..... + a1 + a0
So, a7 + a6 + a5 + ..... + a1 + a0 = 27 = 128
Hence, correct option is (c).
Solution 30
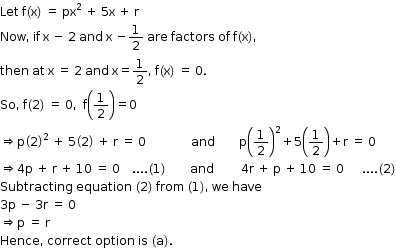
Solution 31

Solution 23
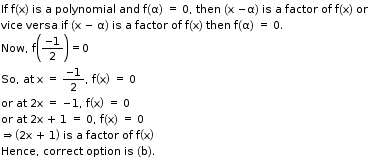
Solution 24
Let p(x) = x3 - 2x2 + ax - b, r(x) = x - 6 and q(x) = x2 - 2x - 3
Then q(x) is a factor of [p(x) - r(x)]
{because if p(x) is divided by q(x), remainder is r(x). So, [p(x) - r(x)] will be exactly divided by q(x)}
Now, q(x) = x2 - 2x - 3 = (x - 3)(x + 1)
If q(x) is a factor of [p(x) - r(x)] then (x - 3) and (x + 1) are also factors of [p(x) - r(x)]
So, at x = 3 and x = -1, p(x) - r(x) will be zero.
Now p(3) - r(3) = 0
i.e. (3)3 - 2(3)2 + a(3) - b - (3 - 6) = 0
i.e. 27 - 18 + 3a - b + 3 = 0
i.e. 3a - b + 12 = 0 ....(1)
And, p(-1) - r(-1) = 0
i.e. (-1)3 - 2(-1)2 + a(-1) - b - (-1 - 6) = 0
i.e. -1 - 2 - a - b + 7 = 0
i.e -a - b + 4 = 0 ....(2)
Subtracting equation (2) from equation (1), we get
4a + 8 = 0
a = -2
From (2), -(-2) - b + 4 = 0
b = 6
Hence, correct option is (c).
Solution 25
x4 + x2 - 20
= x4 + 5x2 - 4x2 - 20
=x2(x2 + 5) - 4(x2 + 5)
= (x2 + 5)(x2 - 4)
So, other factor is x2 - 4.
Hence, correct option is (a).
Solution 26