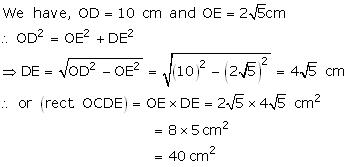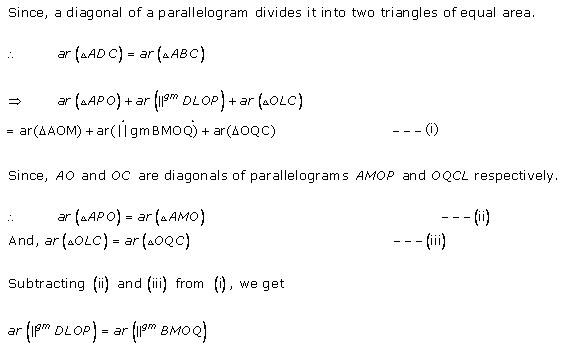Class 9 RD SHARMA Solutions Maths Chapter 14 - Areas of Parallelograms and Triangles
Areas of Parallelograms and Triangles Exercise Ex. 14.1
Solution 1
(i) ΔAPB and trapezium ABCD are on the same base AB and between the same parallels AB and CD.
(ii) Parallelograms ABCD and APQD are on the same base AD and between the same parallels AD and BQ.
(iii) Parallelogram ABCD and ΔPQR are between the same parallels AD and BC but they are not on the same base.
(iv) ΔQRT and parallelogram PQRS are on the same base QR and between the same parallels QR and PS.
(v) Parallelogram PQRS and trapezium SMNR are on the same base SR but they are not between the same parallels.
(vi) Parallelograms PQRS, AQRD, BQRC are between the same parallels. Also, parallelograms PQRS, BPSC and APSD are between the same parallels.
Areas of Parallelograms and Triangles Exercise Ex. 14.2
Solution 1
We know that,
Area of parallelogram = Base x corresponding attitude
Area of parallelogram ABCD = CD x AE = AD x CF
16 cm x 8 cm = AD x 10 cm
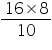 cm = 12.8 cm.
cm = 12.8 cm.Solution 2
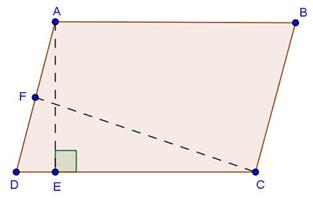
Solution 3

Solution 4

Areas of Parallelograms and Triangles Exercise Ex. 14.3
Solution 1
Solution 2

Solution 3

Solution 4

Solution 5
Solution 6
Solution 7

Solution 8
Solution 9
Solution 10

Solution 11

Solution 12
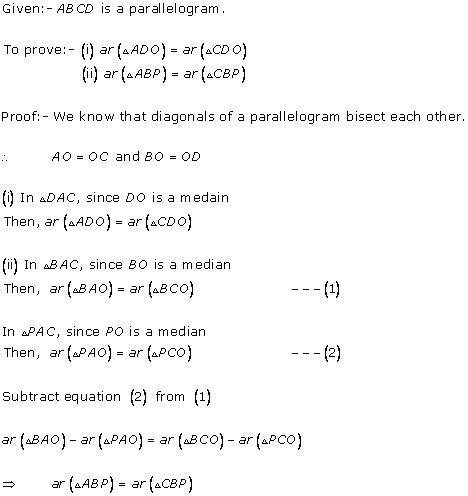
Solution 13
Solution 14
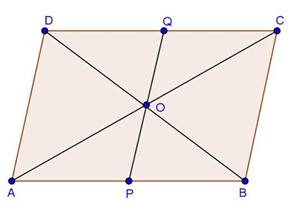
Solution 15
Draw a line l through A parallel to BC.
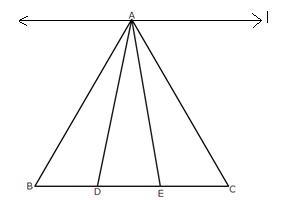
Given that, BD = DE = EC.
We observe that the triangles ABD, ADE and AEC are on the equal bases and between the same parallels l and BC. Therefore, their areas are equal.
Hence, ar (ΔABD) = ar (ΔADE) = ar(ΔAEC).
Solution 16
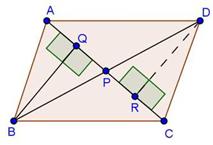

Solution 17
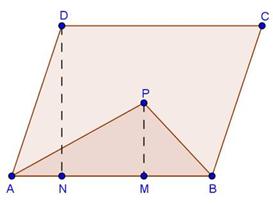

Solution 18
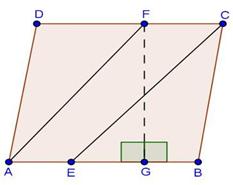

Solution 19
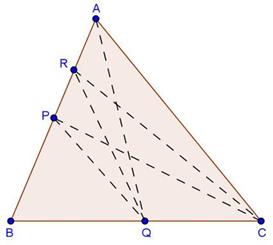
(i) 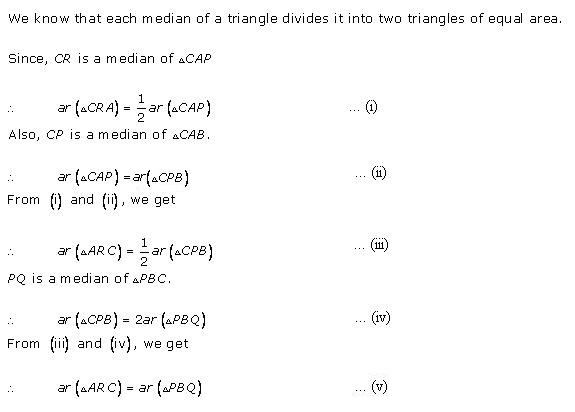
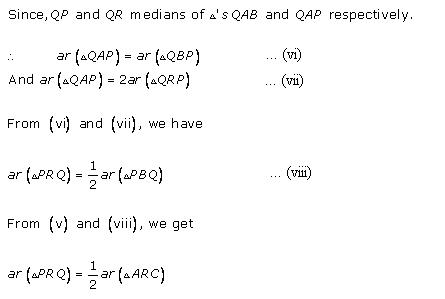
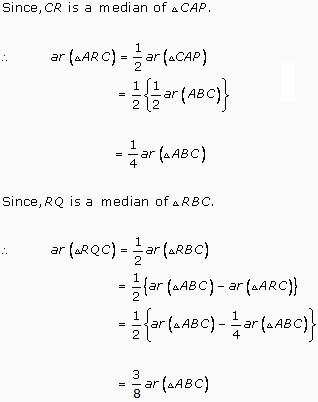
Solution 20
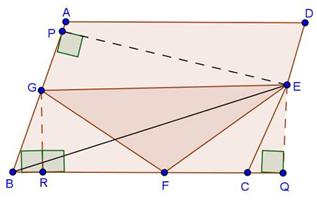


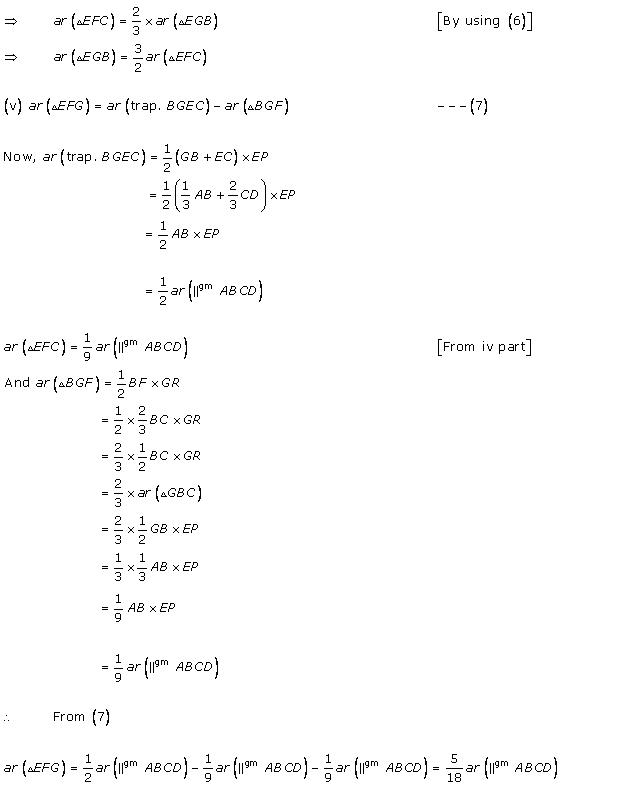
Solution 21

Solution 22

Solution 23
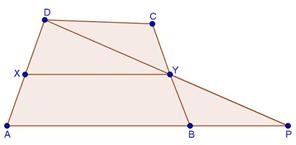


Solution 24
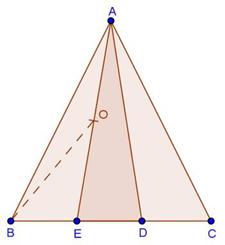

Solution 25

Solution 26
Solution 27
Solution 28
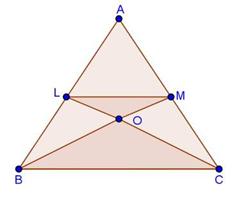

Solution 29
Given, ABC and BDE are two equilateral triangles.
Let AB = BC = CA = x. Then, BD = ![]() = DE = BE
= DE = BE
(i) We have,
ar(![]() ABC) =
ABC) = ![]() x2
x2
ar (![]() BDE) =
BDE) = ![]()
![]() ar(
ar(![]() BDE) =
BDE) = ![]() ar (
ar (![]() ABC)
ABC)
(ii) It is given that triangles ABC and BED are equilateral triangles.
![]() ACB =
ACB = ![]() DBE = 60o
DBE = 60o
![]() BE||AC(Since, alternate angles are equal)
BE||AC(Since, alternate angles are equal)
Triangles BAE and BEC are on the same base BE and between the same parallels BE and AC.
![]() ar (
ar (![]() BAE) = ar(
BAE) = ar(![]() BEC)
BEC)
![]() ar (
ar (![]() BAE) =2 ar (
BAE) =2 ar (![]() BDE)
BDE)
[![]() ED is a median of
ED is a median of ![]() EBC
EBC ![]() ar(
ar(![]() BEC) = 2ar(
BEC) = 2ar(![]() BDE)]
BDE)]
![]() ar (
ar (![]() BDE) =
BDE) = ![]() ar(
ar(![]() BAE)
BAE)
(iii) Since ![]() ABC and
ABC and ![]() BDE are equilateral triangles.
BDE are equilateral triangles.
![]()
![]() ABC = 60o and
ABC = 60o and ![]() BDE = 60o
BDE = 60o
![]()
![]() ABC =
ABC = ![]() BDE
BDE
![]() AB||DE(Since, alternate angles are equal)
AB||DE(Since, alternate angles are equal)
Triangles BED and AED are on the same base ED and between the same parallels AB and DE.
![]() ar (
ar (![]() BED) = ar(
BED) = ar(![]() AED)
AED)
![]() ar (
ar (![]() BED) ar(
BED) ar(![]() EFD) = ar(
EFD) = ar(![]() AED) ar(
AED) ar(![]() EFD)
EFD)
![]() ar(
ar(![]() BEF) = ar(
BEF) = ar(![]() AFD)
AFD)
(iv) Since ED is a median of ![]() BEC
BEC
![]() ar (
ar (![]() BEC) = 2 ar (
BEC) = 2 ar (![]() BDE)
BDE)
![]() ar (
ar (![]() BEC) =
BEC) = ![]() ar (
ar (![]() ABC)[From (i), ar (
ABC)[From (i), ar (![]() BDE) =
BDE) = ![]() ar (
ar (![]() ABC)]
ABC)]
![]() ar(
ar(![]() BEC) =
BEC) = ![]() ar (
ar (![]() ABC)
ABC)
![]() ar (
ar (![]() ABC) = 2 ar (
ABC) = 2 ar (![]() BEC)
BEC)
(v) Let h be the height of vertex E, corresponding to the side BD in triangle BDE.
Let H be the height of vertex A, corresponding to the side BC in triangle ABC.
From part (i),
ar(![]() BDE) =
BDE) = ![]() ar (
ar (![]() ABC)
ABC)

From part (iii),
ar (![]() BFE) = ar (
BFE) = ar (![]() AFD)
AFD)
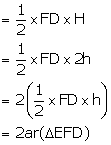
(vi) ar (![]() AFC) = ar (
AFC) = ar (![]() AFD) + ar (
AFD) + ar (![]() ADC)
ADC)
= ar (![]() BFE) +
BFE) + ![]() ar (
ar (![]() ABC)
ABC)
(Using part (iii); and AD is the median of ![]() ABC)
ABC)
= ar (![]() BFE) +
BFE) + ![]() 4 ar (
4 ar (![]() BDE)(Using part (i))
BDE)(Using part (i))
= ar (![]() BFE) + 2 ar (
BFE) + 2 ar (![]() BDE) (2)
BDE) (2)
Now, from part (v),
ar (![]() BFE) = 2ar (
BFE) = 2ar (![]() FED) (3)
FED) (3)
ar (![]() BDE) = ar (
BDE) = ar (![]() BFE) + ar (
BFE) + ar (![]() FED)
FED)
= 2 ar (![]() FED) + ar (
FED) + ar (![]() FED)
FED)
= 3 ar (![]() FED) (4)
FED) (4)
From (2), (3) and (4), we get,
ar (![]() AFC) = 2ar (
AFC) = 2ar (![]() FED) + 2
FED) + 2 ![]() 3 ar (
3 ar (![]() FED) = 8 ar (
FED) = 8 ar (![]() FED)
FED)
Hence, ar (![]() FED) =
FED) = ![]() ar(AFC)
ar(AFC)
Solution 30
(i) In ![]() MBC and
MBC and ![]() ABD, we have
ABD, we have
MB = AB
BC = BD
And ![]() MBC =
MBC = ![]() ABD
ABD
[![]()
![]() MBC and
MBC and ![]() ABD are obtained by adding
ABD are obtained by adding ![]() ABC to a right angle]
ABC to a right angle]
So, by SAS congruence criterion, we have
![]() MBC
MBC ![]()
![]() ABD
ABD
![]() ar (
ar (![]() MBC) = ar(
MBC) = ar(![]() ABD) (1)
ABD) (1)
(ii) Clearly, triangle ABD and rectangle BYXD are on the same base BD and between the same parallels AX and BD.
![]() ar(
ar(![]() ABD) =
ABD) = ![]() ar (rect. BYXD)
ar (rect. BYXD)
![]() ar (rect. BYXD) = 2 ar(
ar (rect. BYXD) = 2 ar(![]() ABD)
ABD)
![]() ar (rect. BYXD) = 2 ar (
ar (rect. BYXD) = 2 ar (![]() MBC)...(2)
MBC)...(2)
[![]() ar (
ar (![]() ABD) = ar (
ABD) = ar (![]() MBC), from (1)]
MBC), from (1)]
(iii) Since triangle MBC and square MBAN are on the same base MB and between the same parallels MB and NC.
![]() 2 ar (
2 ar (![]() MBC) = ar (MBAN) (3)
MBC) = ar (MBAN) (3)
From (2) and (3), we have
ar (sq. MBAN) = ar(rec. BYXD)
(iv) In triangles FCB and ACE, we have
FC = AC
CB = CE
And, ![]() FCB =
FCB = ![]() ACE
ACE
[![]()
![]() FCB and
FCB and ![]() ACE are obtained by adding
ACE are obtained by adding ![]() ACB to a right angle]
ACB to a right angle]
So, by SAS congruence criterion, we have
![]() FCB
FCB ![]()
![]() ACE
ACE
(v) We have,
![]() FCB
FCB ![]()
![]() ACE
ACE
![]() ar (
ar (![]() FCB) = ar (
FCB) = ar (![]() ACE)
ACE)
Clearly, ![]() ACE and rectangle CYXE are on the same base CE ad between the same parallels CE and AX.
ACE and rectangle CYXE are on the same base CE ad between the same parallels CE and AX.
![]() 2 ar (
2 ar (![]() ACE) = ar (CYXE)
ACE) = ar (CYXE)
![]() 2 ar (
2 ar (![]() FCB) = ar (CYXE) (4)
FCB) = ar (CYXE) (4)
(vi) Clearly, ![]() FCB and rectangle FCAG are on the same base FC and between the same parallels FC and BG.
FCB and rectangle FCAG are on the same base FC and between the same parallels FC and BG.
![]() 2ar (
2ar (![]() FCB) = ar(FCAG) (5)
FCB) = ar(FCAG) (5)
From (4) and (5), we get
ar(CYXE) = ar (ACFG)
(vii) Applying Pythagoras theorem in ![]() ACB, we have
ACB, we have
BC2 = AB2 + AC2
![]()
Areas of Parallelograms and Triangles Exercise 14.62
Solution 19

Solution 20

Solution 17

Solution 18

Areas of Parallelograms and Triangles Exercise 14.60
Solution 1
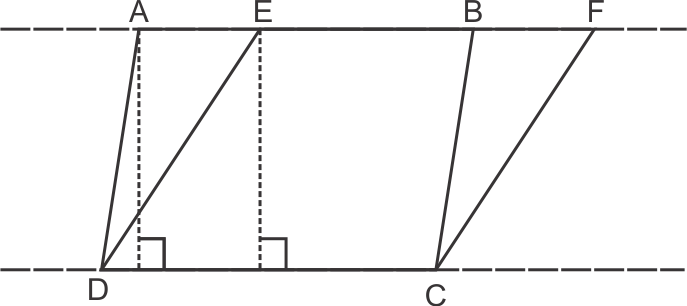
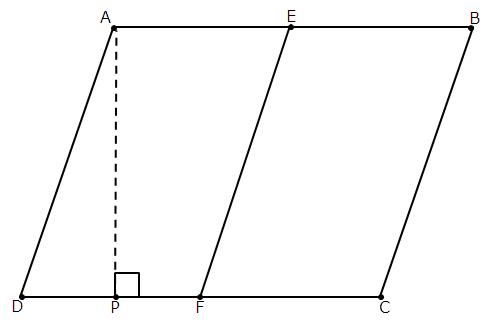
Area of parallelogram = Base × height
Base = Length of base
Height = distance between Base and Side parallel to it
In figure, there are two Parallelograms.
Base of both is same, and because both lie under same parallels that's why height is also same.
Thus, the Ratio of Areas of both parallelogram = 1 : 1
Hence, correct option is (c).
Solution 2
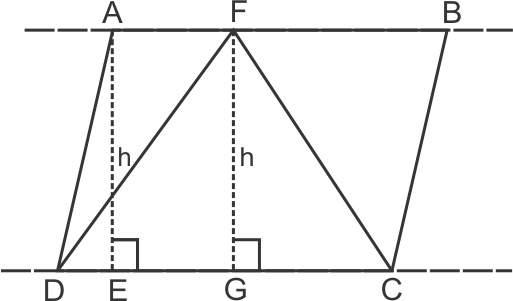
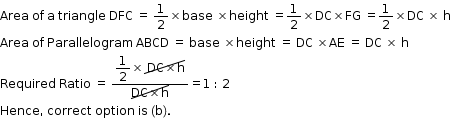
Solution 3
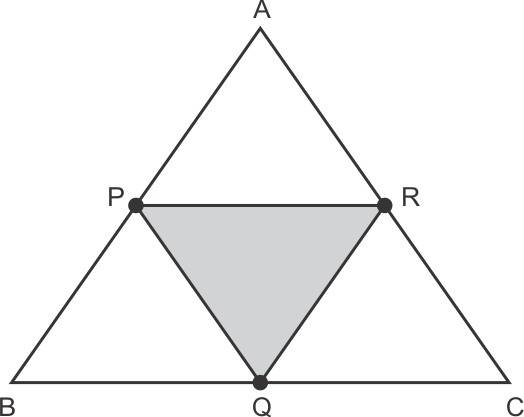
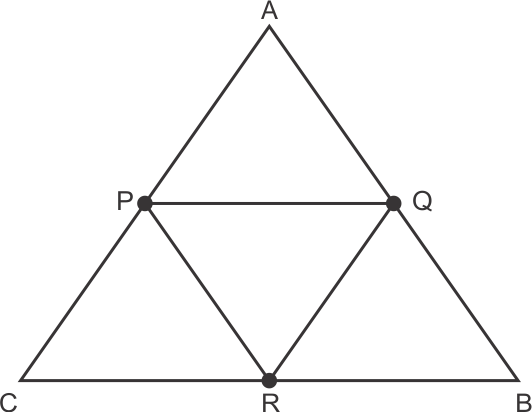
When a triangle is formed by joining the mid-points of sides of a triangle, the triangle formed is Congruent to triangles formed around that.
i.e. ΔPQR is congruent to ΔRPA, ΔQBP & ΔCQR.
Hence, Area of all four triangles formed inside ΔABC is same.
So (4 × Area of any one Δ) = Area of ΔABC
4 × (Area of ΔPQR) = 24 sq. units
Area of ΔPQR = 6 sq. units
Hence, correct option is (b).
Solution 4
A median divides the base in two equal parts but height of a triangle remains the same.
Now, since bases and heights are equal, areas of both Δs are equal.
Hence, correct option is (d).
Solution 5
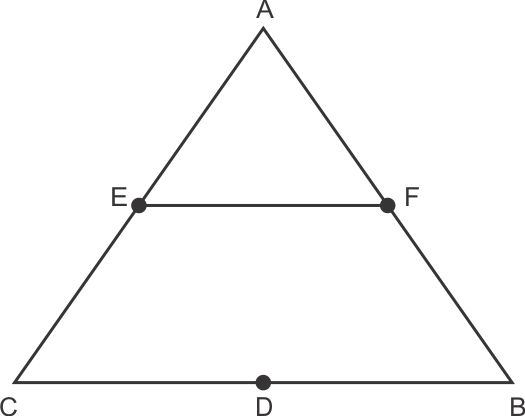

Solution 6
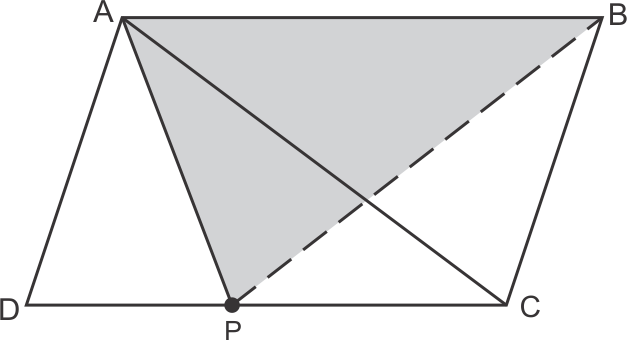

Areas of Parallelograms and Triangles Exercise 14.61
Solution 7
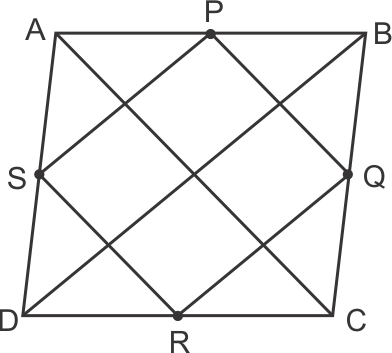

Solution 8
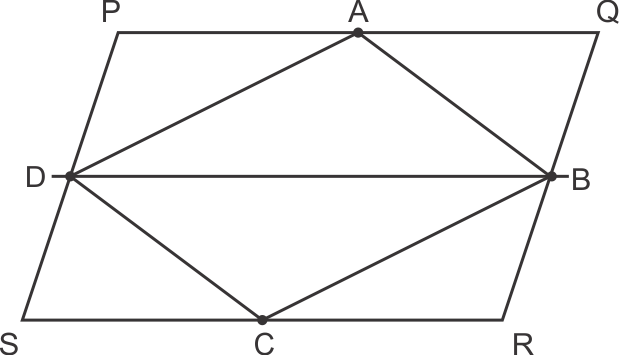

Solution 9

Solution 10

Solution 11

Solution 12
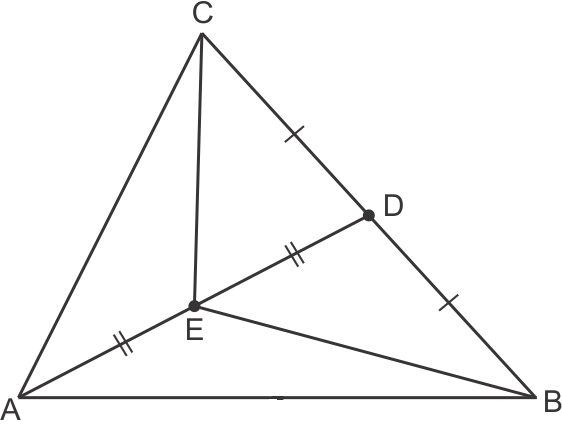
E is the mid-point of AD and CE is median of ΔACD.
Hence Ar(ΔAEC) = Ar(ΔCED) = 4 cm2 ....(1)
(Median divides a Δ in two two equal Areas)
Also AD is median of ΔABC and and ED is median of ΔBEC.
So Ar(ΔBED) = Ar(CED) = 4 cm2 [From eq (1)]
So Ar(ΔBEC) = Ar(ΔBED) + Ar(ΔCED) = 4 + 4 = 8 cm2
Hence, correct option is (c).
Solution 13
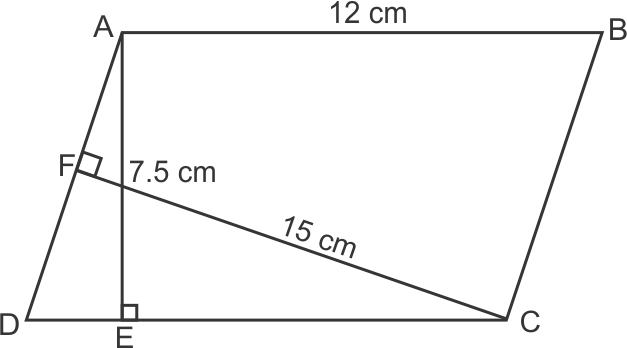
Area of parallelogram = AD × FC = AB × AE
Thus,
AD × 15 = 12 × 7.5
AD = 6 cm
Hence, correct option is (b).
Solution 14

Solution 15

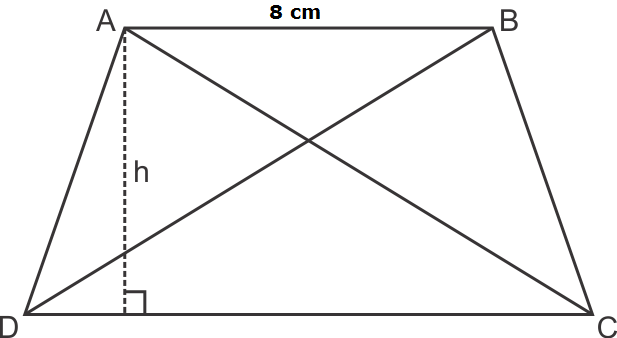
ΔABD & ΔABC have same base AB and are between same parallels.
Then,
Ar(ΔABD) = Ar(ΔABC)
But Ar(ΔAOB) is common in both.
Thus, Ar(ΔAOD) = Ar(ΔBOC)
Hence, correct option is (b).
Solution 16