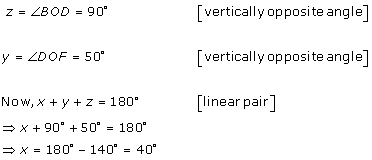
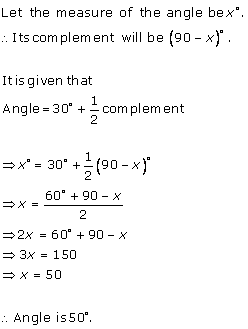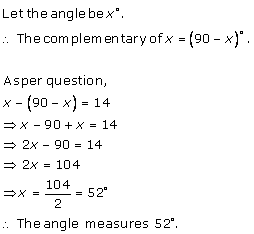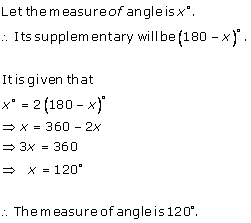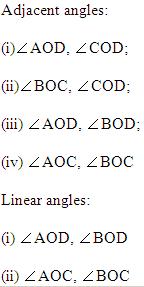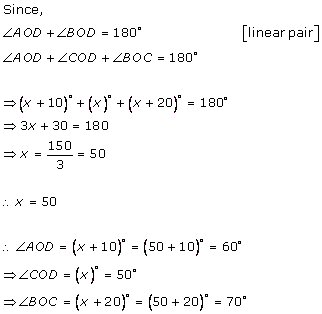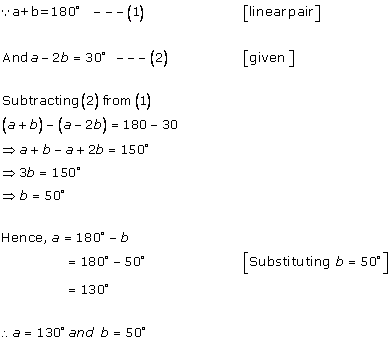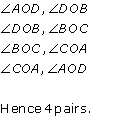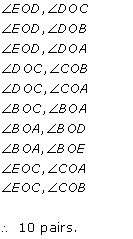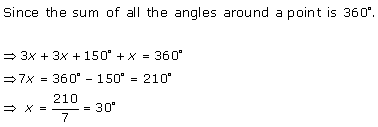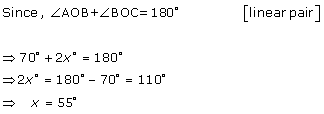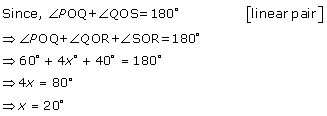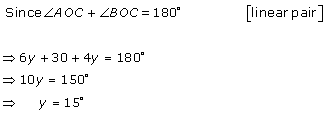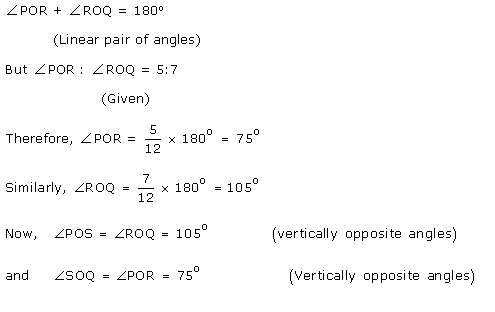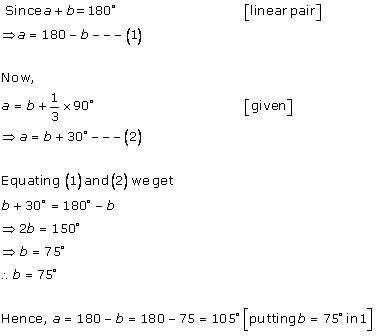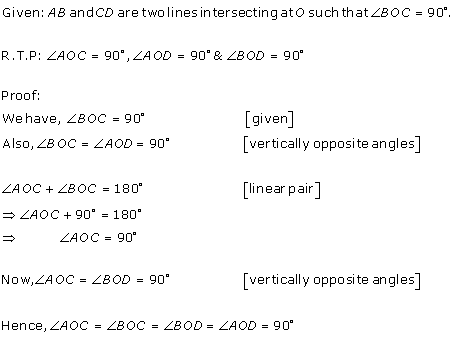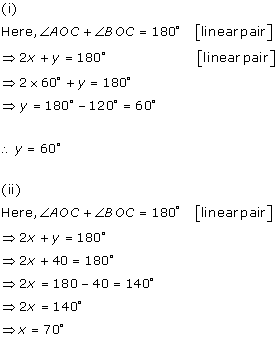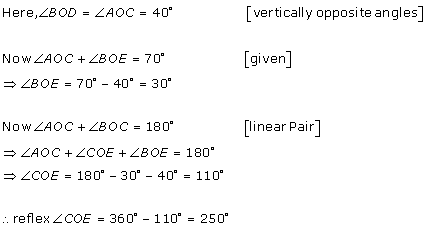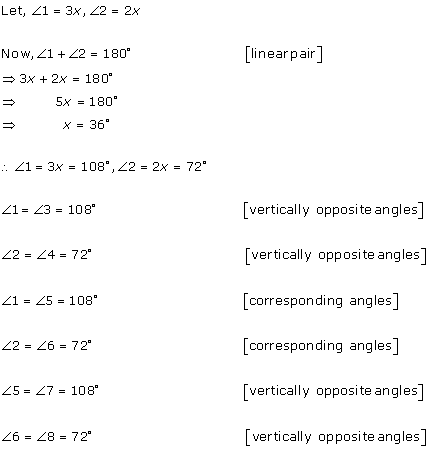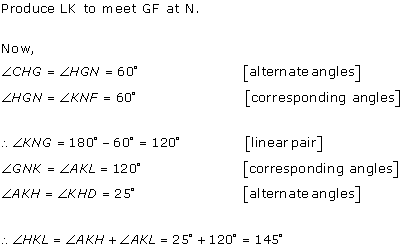RD SHARMA Solutions for Class 9 Maths Chapter 10 - Lines and Angles

Page / Exercise

Chapter 10 - Lines and Angles Exercise Ex. 10.1

Solution 1

Solution 2

(i) 54°

Since, the sum of an angle and its supplement is 180°

∴Its supplement will be 180° - 54° = 126°.


(ii) 132°

Since, the sum of an angle and its supplement is 180°

∴Its supplement will be 180° - 132° = 48°.


(iii) 138°

Since, the sum of an angle and its supplement is 180°

∴Its supplement will be 180° - 138° = 42°.

Solution 3

Solution 4

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10

Solution 11

Solution 12

Solution 13

Let the measure of the angle be xo.

Its complement will be (90o - xo) and its supplement will be (180o - xo).

Supplement of thrice of the angle = (180o - 3xo)

According to the given information:

(90o - xo) = (180o - 3xo)

3x - x = 180 - 90

2x = 90

x = 45

Thus, the measure of the angle is 45o.

The measure of the angle is 45o

Solution 14

Chapter 10 - Lines and Angles Exercise Ex. 10.2

Solution 1

 

Solution 2

Solution 3

 

 

 

Solution 4

 

Solution 5

 

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10

Solution 11

Solution 12

Solution 13

Solution 14

Solution 15

Solution 16

Solution 17

Solution 18

Solution 19
Given that OR ⊥ PQ  
 
∴ POR = 90o   
 
    ⇒ ∠POS  + ∠SOR = 90o
 
∠ROS = 90o  - ∠POS                ... (1)
 
    ∠QOR = 90o                     (As OR ⊥ PQ) 
 
   ∠QOS - ∠ROS = 90o
 
    ∠ROS = ∠QOS - 90o             ... (2)
 
    On adding equations (1) and (2), we have
 
    2 ∠ROS = ∠QOS - ∠POS

Chapter 10 - Lines and Angles Exercise Ex. 10.3

Solution 1

Solution 2

Solution 3

Solution 4

Solution 5



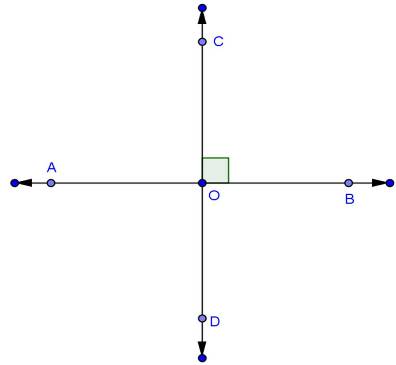
Solution 6

Solution 7

Solution 8



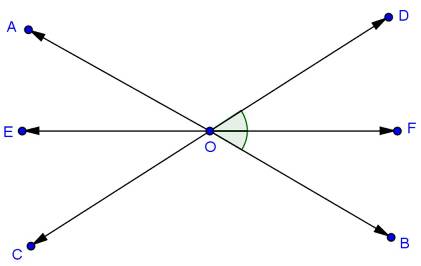
Solution 9

Solution 10

(i) True

(ii) False

(iii) False

(iv) True

Solution 11

(i) obtuse.

(ii) 180o

(iii) uncommon

Solution 12



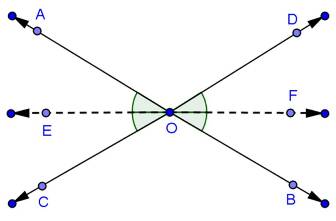
Solution 13



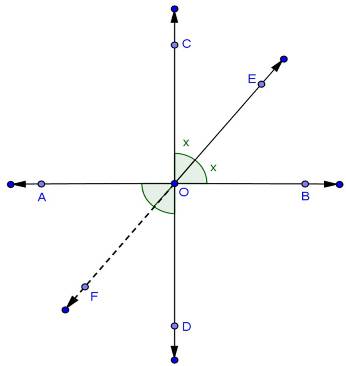
Chapter 10 - Lines and Angles Exercise Ex. 10.4

Solution 1

Solution 2

Solution 20

Solution 3

Solution 4

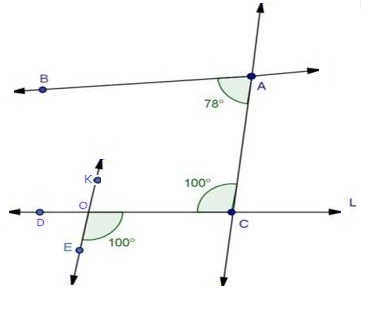
Solution 5

Solution 6



Solution 7



Solution 8

Let AB and CD be perpendicuar to line MN.


Solution 9

Solution 10

Solution 11

Let AB and CD be perpendicuar to line MN.


Solution 12



Solution 13




Solution 14

Solution 15

Solution 16

Solution 17


Solution 18

Solution 19

Solution 21

Solution 22

Solution 23

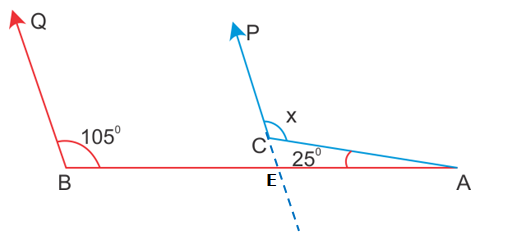
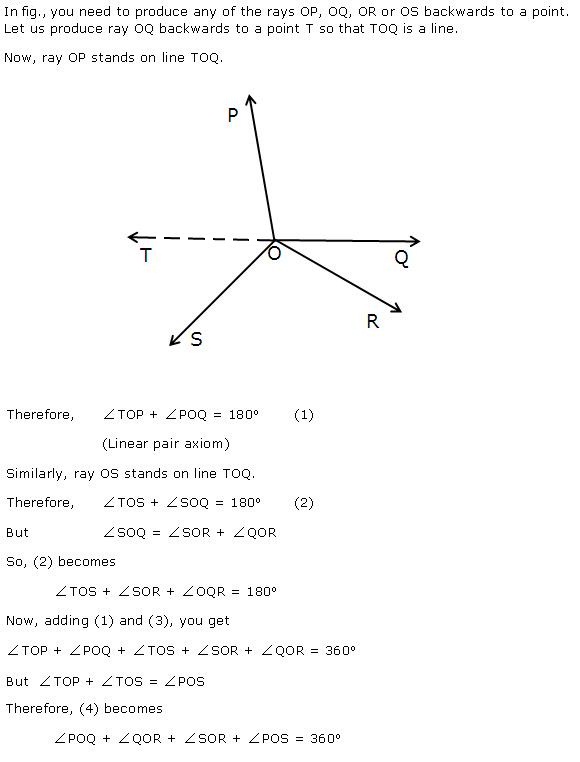
Consider the angles AOB and ACB.



Solution 24

Solution 25

Solution 26

 



Solution 27

Chapter 10 - Lines and Angles Exercise 10.51

Solution 1

begin mathsize 11px style Let space the space required space angle space be space straight theta. Then comma space measure space of space its space supplement space equals space 180 degree space minus space straight theta According space to space question comma space we space have straight theta space equals space 3 open parentheses 180 space minus space straight theta close parentheses rightwards double arrow straight theta equals 540 to the power of ring operator space minus space 3 straight theta rightwards double arrow 4 straight theta space equals space 540 to the power of ring operator rightwards double arrow straight theta space equals space 135 to the power of ring operator Hence comma space correct space option space is space left parenthesis straight b right parenthesis. end style

Solution 2

begin mathsize 11px style angle space AOC space plus space angle space COB space plus space angle space BOD space plus space angle space AOD space equals space 360 to the power of ring operator space space space space.... left parenthesis 1 right parenthesis Now comma space angle space AOC space plus space angle space COB space plus space angle space BOD space equals space 274 to the power of ring operator space space space space space space open parentheses Given close parentheses space.... left parenthesis 2 right parenthesis From space left parenthesis 1 right parenthesis space and space left parenthesis 2 right parenthesis comma 274 to the power of ring operator plus space angle space AOD space equals space 360 ring operator rightwards double arrow angle space AOD space equals space 360 degree space minus space 274 degree rightwards double arrow angle space AOD space equals space 86 to the power of ring operator Hence comma space correct space option space is space left parenthesis straight a right parenthesis. end style

Solution 3

begin mathsize 11px style angle space BOD space and space angle space BOC space form space straight a space linear space pair. therefore space angle space BOD space plus space angle space BOC space equals space 180 to the power of ring operator rightwards double arrow 63 to the power of ring operator space plus space angle space BOC space equals space 180 to the power of ring operator rightwards double arrow angle space BOC space equals 117 to the power of ring operator Hence comma space correct space option space is space left parenthesis straight b right parenthesis. end style

Solution 4

begin mathsize 12px style Let space two space lines space AB space and space CD space intersect space each space other space at space straight O. Now space we space can space see space from space figure space any space two space adjacent space angles comma angle space AOD space & space angle space DOB comma space angle space DOB space & space angle space BOC space etc space are space supplementary space because space their space sum space is space 180 degree. angle space AOD space plus space angle space DOB space equals space 180 to the power of ring operator angle space DOB space plus space angle BOC space equals space 180 to the power of ring operator So space two space adjacent space angles space are space always space supplementary. Now space two space opposite space angle space like space angle space AOC space & space angle space DOB comma space angle space AOD space & space angle space COB are space always space equal space to space each space other space as space they space are space vertically space opposite space angles angle space AOC space equals space angle space DOB angle space AOD space equals space angle space COB Hence space statement space left parenthesis ii right parenthesis space and space left parenthesis iii right parenthesis space are space correct Hence comma space correct space option space is space left parenthesis straight b right parenthesis. end style

Solution 5

begin mathsize 11px style angle POR space equals space 3 straight x space and space angle QOR space equals space 2 straight x space plus 10 to the power of ring operator space From space figure comma space we space can space see space that space angle space POR space & space angle space QOR space are space two space adjacent space angles space and space are space supplement. rightwards double arrow angle POR space plus space angle QOR space equals space 180 to the power of ring operator rightwards double arrow 3 straight x space plus space 2 straight x space plus space 10 to the power of ring operator space equals 180 to the power of ring operator space space rightwards double arrow 5 straight x space equals space 170 to the power of ring operator space rightwards double arrow straight x space equals space 34 to the power of ring operator straight H ence comma space correct space option space is space left parenthesis straight b right parenthesis. end style

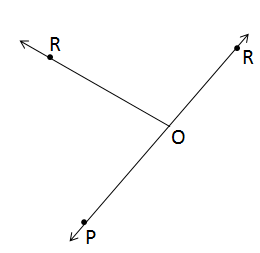
Solution 6

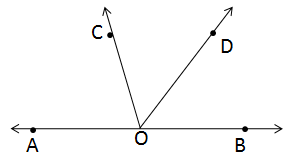
begin mathsize 11px style From space Figure comma space we space can space see space angle AOC space plus space angle COD space plus space angle BOD space equals space 180 to the power of ring operator But comma space angle AOC space plus space angle BOD space equals space 85 to the power of ring operator space space space space space.... left parenthesis Given right parenthesis rightwards double arrow 85 to the power of ring operator space plus space angle COD space equals space 180 to the power of ring operator rightwards double arrow angle COD space equals space 95 to the power of ring operator Hence comma space correct space option space is space left parenthesis straight c right parenthesis. end style

Solution 7

begin mathsize 11px style From space figure comma space we space can space see space angle straight x to the power of ring operator equals angle space straight y to the power of ring operator space space space space space left parenthesis vertically space opposite space angles right parenthesis space Also comma space angle 3 straight x degree plus angle straight y degree plus angle 2 straight x degree space equals space 180 degree Now comma space angle straight x degree equals angle straight y to the power of ring operator therefore space angle 3 straight y to the power of ring operator space plus space angle straight y to the power of ring operator space plus space angle 2 straight y to the power of ring operator space equals space 180 to the power of ring operator rightwards double arrow angle 6 straight y to the power of ring operator space equals space 180 to the power of ring operator rightwards double arrow angle straight y to the power of ring operator equals 30 to the power of ring operator Hence comma space correct space option space is space left parenthesis straight b right parenthesis. end style

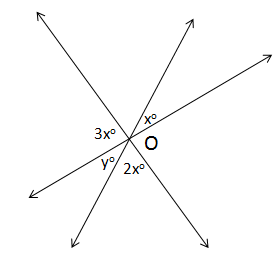
Chapter 10 - Lines and Angles Exercise 10.52

Solution 8

begin mathsize 12px style From space figure comma space we space can space see space that angle BOD space plus space angle AOD space equals space 180 degree angle BOD space equals space 90 degree space left parenthesis Given right parenthesis rightwards double arrow angle AOD space equals space 180 degree space minus space 90 degree space equals space 90 degree Now comma space straight x degree space equals space angle COE space equals space angle FOD space space space space space left parenthesis opposite space angles space are space equal right parenthesis Now comma space angle AOF space plus space angle FOD space equals space 90 degree space equals space angle AOD rightwards double arrow 3 straight x degree space plus space 10 degree space plus space straight x degree space equals space 90 degree rightwards double arrow 4 straight x degree space equals space 80 degree rightwards double arrow straight x degree space equals space 20 degree Hence comma space correct space opiton space is space left parenthesis straight c right parenthesis. end style

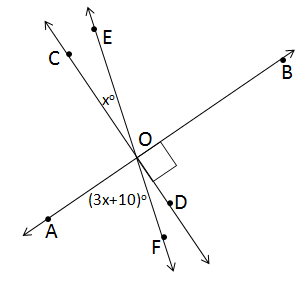
Solution 9

begin mathsize 12px style From space figure comma space we space can space see space that angle straight a degree space plus space angle straight b degree space plus space angle straight c degree space equals space angle FOC space equals space 180 degree Also comma space angle straight b degree space equals space angle straight e degree space space space space left parenthesis opposite space angles right parenthesis So comma space angle straight a degree space plus space angle straight e degree space plus space angle straight c degree space equals space 180 degree space space space space space space rightwards double arrow space left parenthesis ii right parenthesis space is space correct Now comma space angle FOB space not equal to space angle DOB rightwards double arrow angle straight a degree space plus space angle straight b degree space not equal to space angle straight d degree space plus space angle straight c degree space space rightwards double arrow left parenthesis straight i right parenthesis space is space incorrect Now comma space space angle straight b degree space equals space angle straight e degree space and space angle straight f degree space equals space angle straight c degree space space space left parenthesis opposite space angles space are space equal right parenthesis Thus comma space angle straight b degree space plus space angle straight f degree equals angle straight e degree space plus space angle straight c degree space rightwards double arrow left parenthesis iii right parenthesis space is space also space correct Hence comma space correct space option space is space left parenthesis straight d right parenthesis. end style

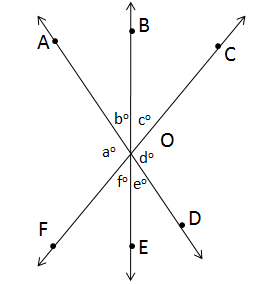
Chapter 10 - Lines and Angles Exercise 10.53

Solution 10

begin mathsize 12px style Let space AB space and space CD space are space two space Parallel space lines space and space PQ space is space transverce space to space it. According space to space Question comma fraction numerator angle BRS over denominator angle DSR end fraction equals 2 over 3 rightwards double arrow angle BRS space equals space 2 over 3 angle DSR space space space.... left parenthesis 1 right parenthesis Now comma space angle CSR space equals space angle BRS space space space space left parenthesis Alternate space angles right parenthesis Also comma space angle CSR space plus space angle DSR space equals space 180 degree rightwards double arrow angle BRS space plus space angle DSR space equals space 180 degree rightwards double arrow 2 over 3 angle DSR space plus space angle DSR space equals space 180 degree rightwards double arrow angle DSR space equals fraction numerator begin display style stack up diagonal strike 180 with 36 on top cross times 3 end style over denominator up diagonal strike 5 end fraction equals 108 degree rightwards double arrow angle BRS equals 2 over 3 cross times 108 degree equals 72 degree Thus comma space angle DSR space equals space 108 degree space and space angle BRS space equals space 72 degree rightwards double arrow Larger space angle space is space angle DSR. Hence comma space correct space option space is space left parenthesis straight c right parenthesis. end style

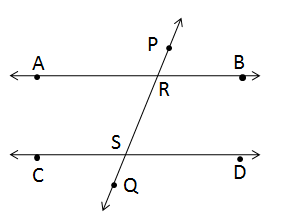
Solution 11

begin mathsize 12px style From space figure comma angle DPQ space plus space angle straight x degree space equals space 180 degree space space left parenthesis linear space pair right parenthesis space space space.... left parenthesis 1 right parenthesis Also comma space angle DPQ space equals space angle AQP space space space space space left parenthesis interior space opposite space angles right parenthesis rightwards double arrow angle DPQ space equals space 120 degree space plus space straight x space space From space left parenthesis 1 right parenthesis comma space 120 degree space plus space straight x space plus space straight x equals space 180 degree rightwards double arrow 2 straight x space equals space 60 degree rightwards double arrow straight x space equals space 30 degree Hence comma space option space left parenthesis straight b right parenthesis space is space correct. end style

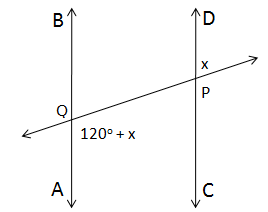
Solution 12

begin mathsize 12px style angle AOC space plus space angle COB space plus space angle BOD space equals space 270 degree space space space left parenthesis Given right parenthesis From space figure comma angle AOC space plus space angle COB space plus space angle BOD space plus space angle DOA space equals space 360 degree rightwards double arrow 270 degree space plus space angle DOA space equals space 360 degree rightwards double arrow angle DOA space equals space 360 degree space minus space 270 degree space equals space 90 degree Now space angle DOA space plus space angle AOC space equals space 180 to the power of ring operator rightwards double arrow angle AOC space equals space 180 degree space minus space 90 degree space equals space 90 degree Hence comma space correct space option space is space left parenthesis straight c right parenthesis. end style

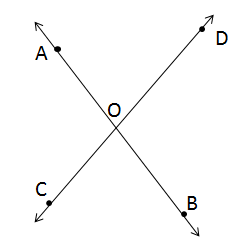
Solution 13

begin mathsize 12px style From space figure comma angle AEF space equals space angle EGH space space space space space space left parenthesis Corresponding space angles right parenthesis rightwards double arrow angle EGH equals angle AEF space equals 95 degree space space Also comma space angle BGH space plus space angle EGH space equals space 180 degree rightwards double arrow angle BGH space equals space 180 degree space minus space angle EGH space equals space 180 degree space minus space 95 degree space equals 85 degree angle BHS space equals 110 degree Now comma space angle BHG space plus space angle space BHS space equals 180 degree rightwards double arrow angle BHG space equals space 180 degree space minus space angle BHS equals space 180 degree space minus space 110 degree equals 70 degree space Now comma space in space triangle BHG angle BGH space plus space angle BHG space plus space straight x space equals space 180 degree space space space left parenthesis Sum space of space all space angles space of space straight a space triangle space is space 180 degree right parenthesis rightwards double arrow 8 5 degree plus 70 degree space plus space straight x degree space equals space 180 degree rightwards double arrow straight x degree space equals space 180 degree space minus space 155 degree space equals 25 degree Hence comma space correct space option space is space left parenthesis straight b right parenthesis. space end style

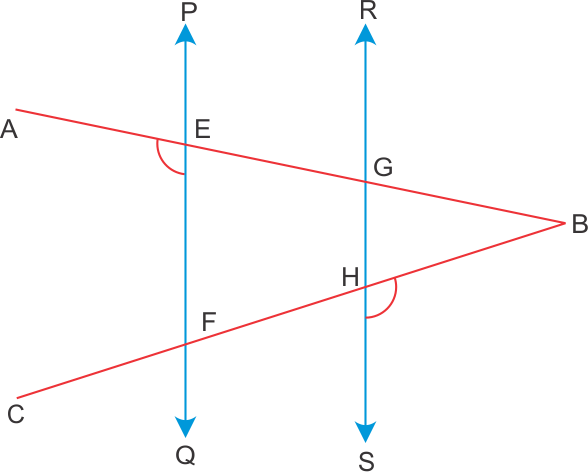
Solution 14

begin mathsize 12px style From space figure comma space angle ERC space equals space angle RPA space space space space space space left parenthesis Correspondence space angles space are space equal right parenthesis rightwards double arrow angle ERC space equals space 37 degree space equals space angle RPA Also comma space angle RPA space equals space angle BPF space space space space space space space space space left parenthesis opposite space angles right parenthesis rightwards double arrow angle RPA space equals space 37 degree space equals space angle BPF Now comma space angle QPB space plus space angle BPF space plus space angle FPG space equals space 180 degree rightwards double arrow straight x degree plus space 37 degree plus space 58 degree space equals space 180 degree rightwards double arrow straight x degree space equals space 85 degree Hence comma space correct space option space is space left parenthesis straight b right parenthesis. end style

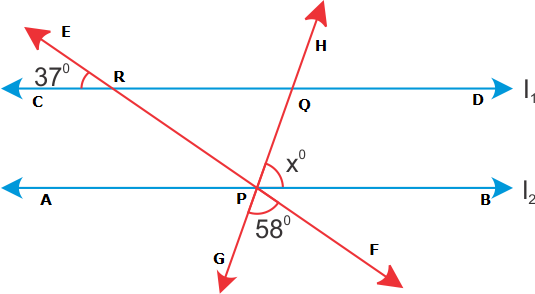
Chapter 10 - Lines and Angles Exercise 10.54

Solution 15

begin mathsize 12px style Let space angle space supplement space of space straight w degree space be space straight a degree. rightwards double arrow straight a degree space equals space 180 degree space minus space straight w degree Now comma space straight a degree space equals space straight x degree space space space space space space space space space open parentheses Alternate space opposite space angles close parentheses rightwards double arrow straight x degree space equals space 180 degree space minus space straight w degree space space.... left parenthesis 1 right parenthesis Now comma space straight y degree space equals space straight z degree space space space.... left parenthesis 2 right parenthesis space space open parentheses Alternate space space angles close parentheses Adding space left parenthesis 1 right parenthesis space and space left parenthesis 2 right parenthesis comma space we space get straight x degree space plus space straight y degree space equals space 180 degree space minus space straight w degree space plus space straight z degree Hence comma space correct space option space is space left parenthesis straight a right parenthesis. end style

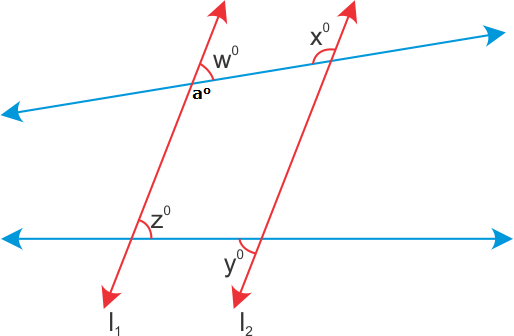
Solution 16

begin mathsize 12px style Let space angle space supplement space of space 3 straight x degree space be space straight z degree rightwards double arrow straight z degree space equals space 180 degree space minus space 3 straight x degree rightwards double arrow angle AHF space plus space angle FHB space equals space 180 degree rightwards double arrow straight z degree space plus space 3 straight x degree space equals space 180 degree rightwards double arrow straight z degree space equals space 180 degree space minus space 3 straight x degree Now comma space straight x degree space plus space straight y degree space equals space 180 degree Also comma space straight x degree space equals space straight z degree space space space space space left parenthesis correspondence space angles right parenthesis rightwards double arrow space straight x degree space equals space 180 degree space minus space 3 straight x degree rightwards double arrow space 4 straight x degree space equals space 180 degree rightwards double arrow space straight x degree space equals space 45 degree straight x degree space plus space straight y degree space equals space 180 degree rightwards double arrow straight y degree space equals space 180 degree space minus space straight x degree space equals space 180 degree space minus space 45 degree space equals space 135 degree Hence comma space correct space option space is space left parenthesis straight c right parenthesis. end style

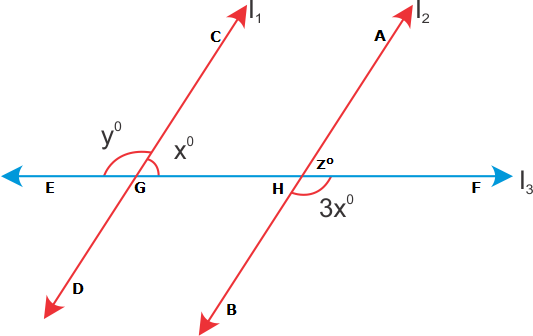
Solution 17

begin mathsize 12px style Fom space figure comma angle EPR space equals space angle PQS space space space space space open parentheses Correspondence space angles space are space equal close parentheses rightwards double arrow angle PQS equals space straight x degree straight A lso comma space angle PQS space equals angle RSD space open parentheses Correspondence space angles space are space equal close parentheses rightwards double arrow angle RSD space equals space straight x degree Now comma space angle RSD space plus space straight y degree space plus space straight y degree space equals space 180 degree rightwards double arrow straight x degree plus space 2 straight y degree space equals 180 degree rightwards double arrow straight y degree equals fraction numerator 180 degree minus straight x degree over denominator 2 end fraction rightwards double arrow straight y degree equals 90 degree minus fraction numerator straight x degree over denominator 2 end fraction Hence comma space correct space option space is space left parenthesis straight c right parenthesis. end style

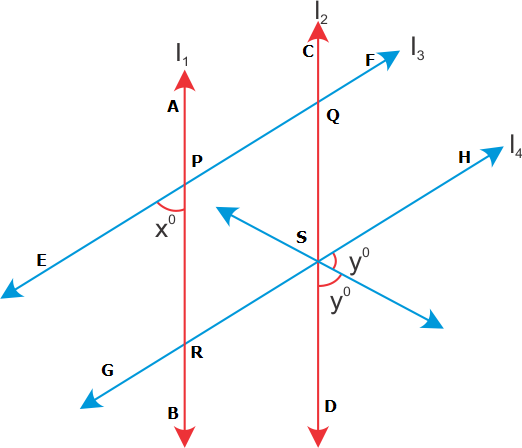
Chapter 10 - Lines and Angles Exercise 10.55

Solution 18

begin mathsize 12px style 3 straight y degree space equals space 2 straight y degree space plus space 25 degree space space space space space space left parenthesis Alternate space angles right parenthesis rightwards double arrow straight y degree space equals space 25 degree space Now comma space straight x degree space plus space 15 degree space equals space 2 straight y degree space plus space 25 degree space space space space space space left parenthesis opposite space angles right parenthesis rightwards double arrow straight x space equals space 2 straight y degree space plus space 25 degree minus 15 degree rightwards double arrow straight x equals 2 straight y degree space plus space 10 degree rightwards double arrow straight x equals 2 cross times space 25 degree plus 10 degree rightwards double arrow straight x space equals 60 degree Hence comma space correct space option space is space left parenthesis straight a right parenthesis. end style

Solution 19

begin mathsize 12px style AB space parallel to space HF space AND space angle CFH equals 28 degree space space space space space space space left parenthesis given right parenthesis angle CFH space equals space angle FDA space space space space open parentheses Correspondence space Angles space are space equal close parentheses rightwards double arrow angle FDA space equals space space 28 degree Now comma space angle FDA space plus space angle FDE space plus space angle EDB space equals space 180 degree rightwards double arrow 28 degree plus angle FDE plus 72 degree equals 180 degree rightwards double arrow angle FDE space equals 80 degree Hence comma space correct space option space is space left parenthesis straight b right parenthesis. end style

Solution 20

begin mathsize 12px style From space figure comma angle ABD space equals space angle CDF space space left parenthesis Correspondence space Angles right parenthesis rightwards double arrow angle CDF equals space 65 degree Now comma space angle FDE space equals space 180 degree space minus space angle CDF space equals 180 degree space minus space 65 degree rightwards double arrow angle FDE space equals space 115 degree In space triangle EDF comma angle FDE space plus space angle DEF space plus space angle EFD space equals space 180 degree rightwards double arrow 115 degree space plus space straight x space plus space 20 degree space equals space 180 degree space open parentheses Sum space of space all space interior space angles space of space straight a space triangle space as space 180 degree close parentheses rightwards double arrow straight x space equals space 180 degree space minus space 20 degree space minus 115 degree equals space 45 degree Hence comma space correct space option space is space left parenthesis straight b right parenthesis. end style

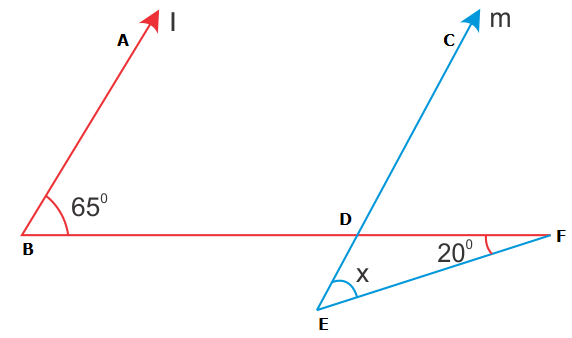
Solution 21

begin mathsize 12px style Extending space line space BA space and space CP space to space meet space at space Point space straight E. angle APE space equals space 180 degree space minus space 148 degree space equals space 32 degree angle EAP space equals space 180 degree space minus space 132 degree space equals 48 degree angle AEP space equals straight x degree space space space space open curly brackets left parenthesis Correspondence space angles right parenthesis space because space AB space parallel to space CD space cut space by space transverse space EC close curly brackets Now comma space in space triangle APE angle APE space plus space angle EAP space plus space angle AEP space equals space 180 degree rightwards double arrow 32 degree space plus space 48 degree space plus space straight x degree space equals space 180 degree rightwards double arrow straight x space equals space 100 degree Hence comma space correct space option space is space left parenthesis straight a right parenthesis. end style

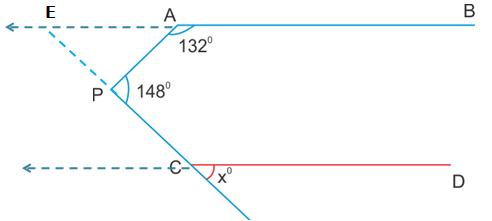
Chapter 10 - Lines and Angles Exercise 10.56

Solution 22

begin mathsize 12px style From space figure comma angle ABC space equals space angle DCE space space space space space..... left parenthesis 1 right parenthesis space space space space open parentheses Corresponding space angles close parentheses angle ECF space equals space 180 degree space minus space angle DCE space space space left parenthesis Supplementry right parenthesis space space space space space space space space space space space space space equals space 180 degree space minus space angle ABC space space space space left square bracket From space left parenthesis 1 right parenthesis right square bracket space space space space space space space space space space space space space space equals space 180 degree space minus space 70 degree rightwards double arrow angle ECF space equals space 110 degree Now comma space in space triangle CEF angle ECF space plus space angle CFE space plus space angle FEC space equals space 180 degree rightwards double arrow 110 degree space plus space straight x space plus space 30 degree space equals space 180 degree rightwards double arrow straight x space equals space 40 degree Hence comma space correct space option space is space left parenthesis straight c right parenthesis. end style

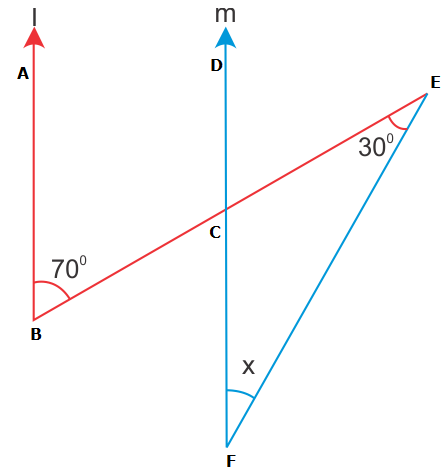
Solution 23

begin mathsize 12px style From space figure comma angle AGE space equals space angle FGB space space left parenthesis opposite space angles right parenthesis rightwards double arrow angle FGB space equals space 65 degree Also comma space angle FGB space equals space angle HJI space space space space space space space space left parenthesis Corresponding space angle right parenthesis rightwards double arrow angle HJI space equals 65 degree Now comma space in space triangle HJI comma angle HJI space plus space angle JIH space plus space angle IHJ space equals space 180 degree rightwards double arrow 65 degree space plus space 40 degree space plus space angle IHJ space equals space 180 degree rightwards double arrow angle IHJ space equals space 180 degree space minus space 65 degree space minus space 40 degree space equals space 75 degree Now comma space straight x space equals space 180 degree space minus space angle IHJ space equals space 180 degree space minus space 75 degree equals space 105 degree Hence comma space correct space option space is space left parenthesis straight a right parenthesis. end style

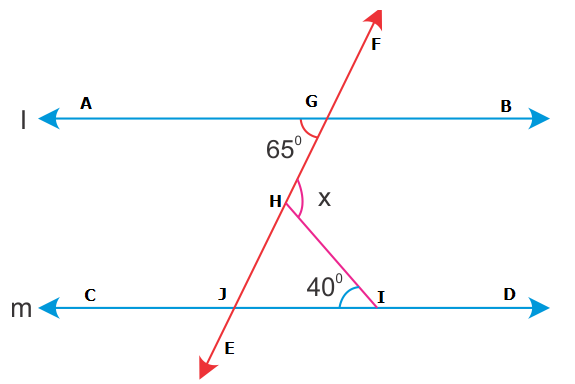
Solution 24

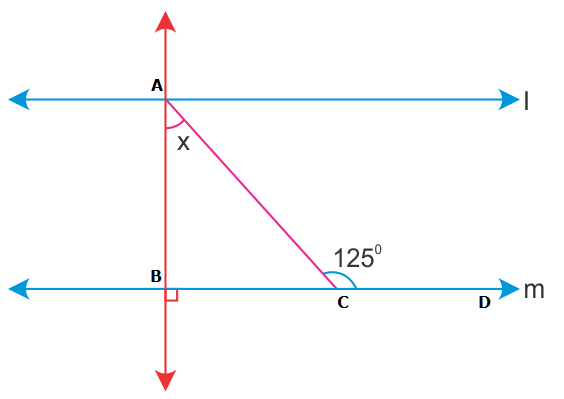
begin mathsize 12px style From space figure comma angle ACB space equals space 180 degree space minus space angle ACD equals space 180 degree space minus space 125 degree equals space 55 degree OR space angle BCA space equals 55 degree In space Right space triangle space ABC angle ABC space plus space angle BCA space plus space angle CAB space equals space 180 degree rightwards double arrow 90 degree space plus space 55 degree space plus space straight x space equals space 180 degree rightwards double arrow straight x space equals space 35 degree Hence comma space correct space option space is space left parenthesis straight a right parenthesis. end style

Solution 25

Correct option (c)

Let one angle be θ

Then, its complementary = 90 - θ

According to question,

2θ = 3(90 - θ)

5θ = 270

θ = 54°

Then,  90 - θ° = 36°

Hence, the smaller angle is 36°.

Hence, correct option is (c).

Chapter 10 - Lines and Angles Exercise 10.57

Solution 26

begin mathsize 12px style From space figure comma space we space can space see space that angle straight x degree space plus space angle straight y degree space plus space angle straight z degree space equals space space 180 degree space space space... left parenthesis 1 right parenthesis Now comma space straight y over straight x equals 5 rightwards double arrow space straight y space equals space 5 straight x And comma space straight z over straight x equals 4 space space space straight z space equals space 4 straight x Substituting space these space value space in space equation space left parenthesis 1 right parenthesis comma space we space have angle space straight x degree space plus space angle 5 straight x degree space plus space angle 4 straight x space equals space space 180 degree rightwards double arrow angle 10 straight x degree space equals space 180 degree rightwards double arrow angle straight x degree space equals space 18 degree space Hence comma space correct space option space is space left parenthesis straight b right parenthesis. end style

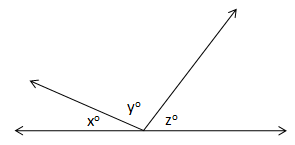
Solution 27

begin mathsize 12px style GH space parallel to space KL rightwards double arrow angle GHK space equals space angle HKL space space space space open parentheses interior space opposite space angles close parentheses Now comma space angle GHK space equals space angle GHD space plus space angle DHR space space space space space space space space space space space space space space space space space space space space space space space space space space equals space open parentheses 180 degree space minus space angle GHC close parentheses space plus space angle DHK space space space space left parenthesis angle GHC space and space angle GHD space are space supplementary right parenthesis space space space space space space space space space space space space space space space space space space space space space space space space space equals space 180 degree space minus space 60 degree space plus space 25 degree space rightwards double arrow angle GHK space equals space 145 degree rightwards double arrow angle HKL space equals space angle GHK space equals space 145 degree space Hence comma space correct space option space is space left parenthesis straight c right parenthesis. end style

Solution 28

begin mathsize 12px style From space figure comma space angle LEB space equals space angle FEL space space space space space space space space left parenthesis EL space is space bisector space of space angle FEB right parenthesis Now comma space angle FEB space equals space 2 angle LEB space equals space 2 cross times 35 degree equals 70 degree Also comma space angle FEB space equals space angle CFE space space space space space left parenthesis Alternate space interior space angles right parenthesis rightwards double arrow angle CFE space equals space 70 degree Now comma space angle CFE space plus space angle CFQ space equals space 180 degree rightwards double arrow 70 degree space plus space angle CFQ space equals space 180 degree rightwards double arrow angle CFQ space equals space 180 degree space minus space 70 degree space equals space 110 degree Hence comma space correct space option space is space left parenthesis straight c right parenthesis. end style

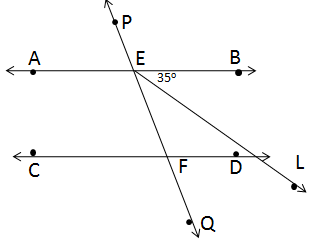
Solution 29

begin mathsize 12px style From space figure comma angle ABD space plus space angle EBD space equals space 180 degree space rightwards double arrow angle EBD space equals space 180 degree space minus space angle ABD space space space space space.... left parenthesis 1 right parenthesis Now comma space angle ABD space equals space straight y degree space plus space 2 straight y degree space plus space straight y degree space rightwards double arrow angle ABD equals space 4 straight y degree space space space.... left parenthesis 2 right parenthesis Substituting space left parenthesis 2 right parenthesis space in space left parenthesis 1 right parenthesis comma space we space have angle EBD space equals space 180 degree space minus space 4 straight y degree Now comma space angle EBD space equals space angle BDC space space space space space open parentheses Alternate space angles close parentheses rightwards double arrow 180 degree space minus space 4 straight y degree equals space 5 straight y degree rightwards double arrow 180 degree space equals space 9 straight y degree rightwards double arrow straight y space equals space 20 degree Hence comma space correct space option space is space left parenthesis straight d right parenthesis. end style

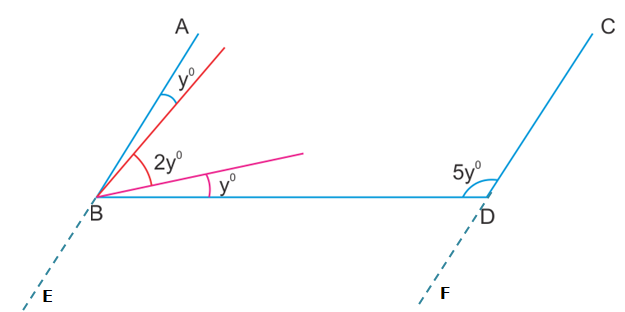
Solution 30

begin mathsize 12px style From space Figure comma angle QBA space equals space angle CEA space space open parentheses Correspondence space angles close parentheses rightwards double arrow angle CEA equals 105 degree space space space space.... left parenthesis 1 right parenthesis In space triangle ACE comma angle CEA plus angle EAC plus angle ACE equals 180 degree rightwards double arrow 105 degree space plus space 25 degree space plus space angle ACE space equals space 180 degree space space space space space left square bracket from space left parenthesis 1 right parenthesis right square bracket rightwards double arrow 130 degree space plus space angle ACE space equals space 180 degree rightwards double arrow angle ACE space equals space 50 degree Now comma space straight x equals angle ACP equals 180 degree space minus space angle ACE equals 180 degree minus 50 degree equals 130 degree Hence comma space correct space option space is space left parenthesis straight a right parenthesis. end style