Class 12-science RD SHARMA Solutions Maths Chapter 15 - Mean Value Theorems
Mean Value Theorems Exercise Ex. 15.1
Solution 1(i)

Solution 1(ii)

Solution 1(iii)

Solution 1(iv)

Solution 1(v)
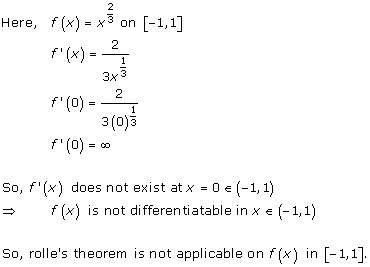
Solution 1(vi)

Solution 2(i)

Solution 2(iii)

Solution 2(iv)

Solution 2(v)

Solution 2(vi)
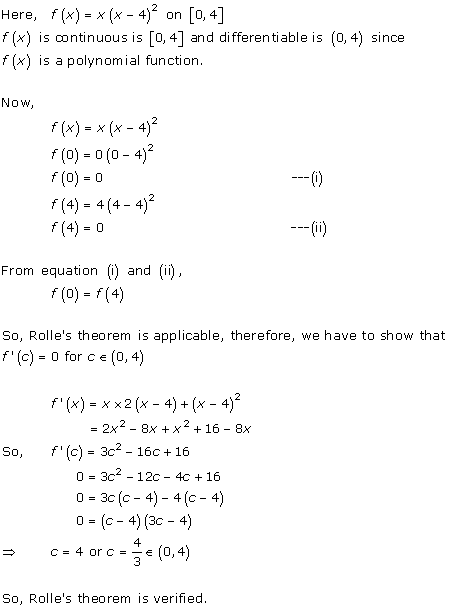
Solution 2(vii)

Solution 2(viii)

Solution 3(i)

Solution 3(ii)

Solution 3(iii)

Solution 3(iv)

Solution 3(v)

Solution 3(vi)

Solution 3(vii)
Here,

Solution 3(viii)

Solution 3(ix)

Solution 3(x)

Solution 3(xi)

Solution 3(xii)

Solution 3(xiii)

Solution 3(xiv)

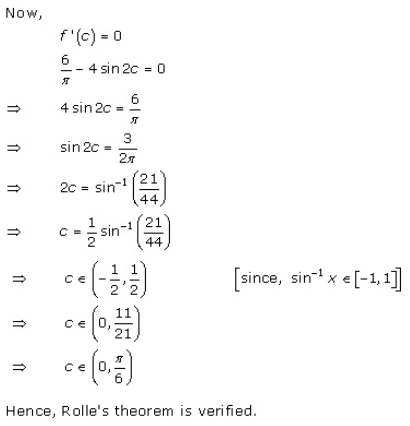
Solution 3(xv)

Solution 3(xvi)

Solution 3(xvii)

Solution 3(xviii)

Solution 7
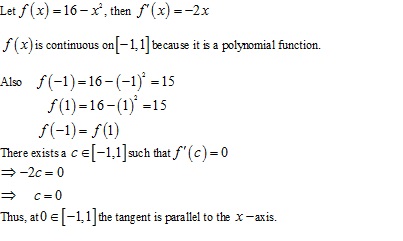
x = 0 then y = 16
Therefore, the point on the curve is (0, 16)
Solution 8(i)

x = 0, then y = 0
Therefore, the point is (0, 0)
Solution 8(ii)

Solution 8(iii)

x = 1/2, then y = - 27
Therefore, the point is (1/2, - 27)
Solution 9

Solution 10



Solution 11
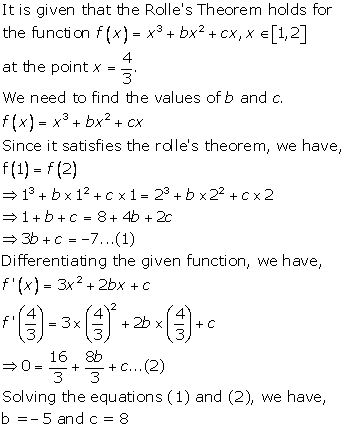
Solution 2(ii)
Given function is ![]()
As the given function is a polynomial, so it is continuous and differentiable everywhere.
Let's find the extreme values
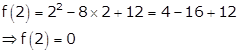
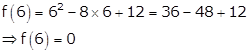
Therefore, f(2) = f(6).
So, Rolle's theorem is applicable for f on [2, 6].
Let's find the derivative of f(x)
![]()
Take f'(x) = 0
![]()
As 4 ∈ [2, 6] and f'(4) = 0.
Thus, Rolle's theorem is verified.
Mean Value Theorems Exercise Ex. 15.2
Solution 1(i)

Solution 1(ii)

Solution 1(iii)

Solution 1(iv)

Solution 1(v)

Solution 1(vi)

Solution 1(vii)

Solution 1(viii)

Solution 1(ix)

Solution 1(x)

Solution 1(xi)

Solution 1(xii)

Solution 1(xiii)

Solution 1(xiv)

Solution 1(xv)

Solution 1(xvi)

Solution 2

Solution 3

Solution 4

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10


Solution 11
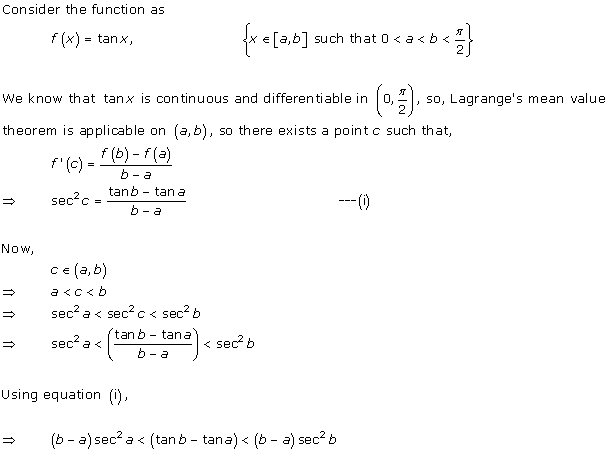
Mean Value Theorems Exercise MCQ
Solution 1
Correct option: (c)

Solution 2
Correct option: (c)

Solution 3
Correct option: (b)
![]()
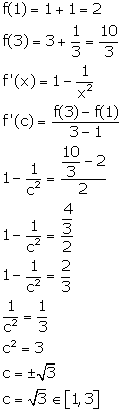
Solution 4
Correct option: (c)
Using statement of Lagrange's mean value theorem function is continuous on [a,b], differentiable on (a,b) then there exists c such that a < x1< b.
Solution 5
Correct option: (b)
ϕ(x) is continuous and differentiable function then using statement of Rolle's theorem f(a)=f(b). Hence, here sin 0=0 also sin п=0. The answer is [0, ![]() ].
].
Solution 6
Correct option: (a)
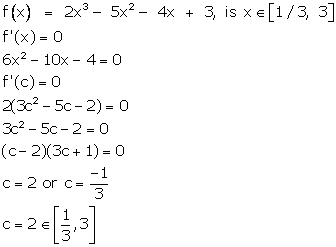
Solution 7
Correct option: (a)

Solution 8
Correct answer: (c)

Solution 9
Correct option: (d)

Solution 10
Correct option: (a)

Solution 11
Correct option: (d)
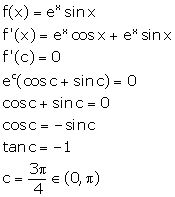
Mean Value Theorems Exercise Ex. 15VSAQ
Solution 1

Solution 2

Solution 3

Solution 4

Solution 5



