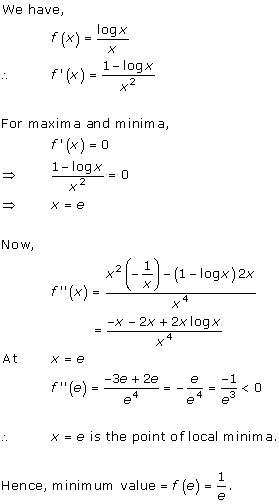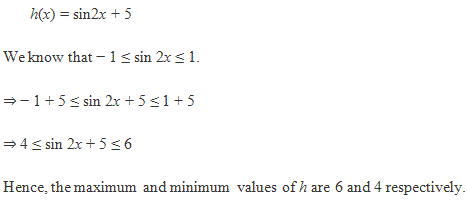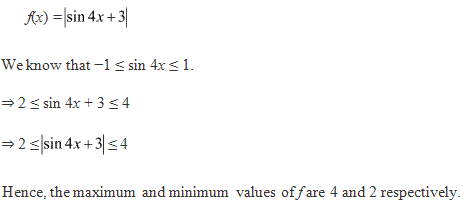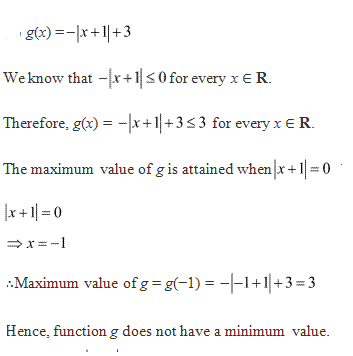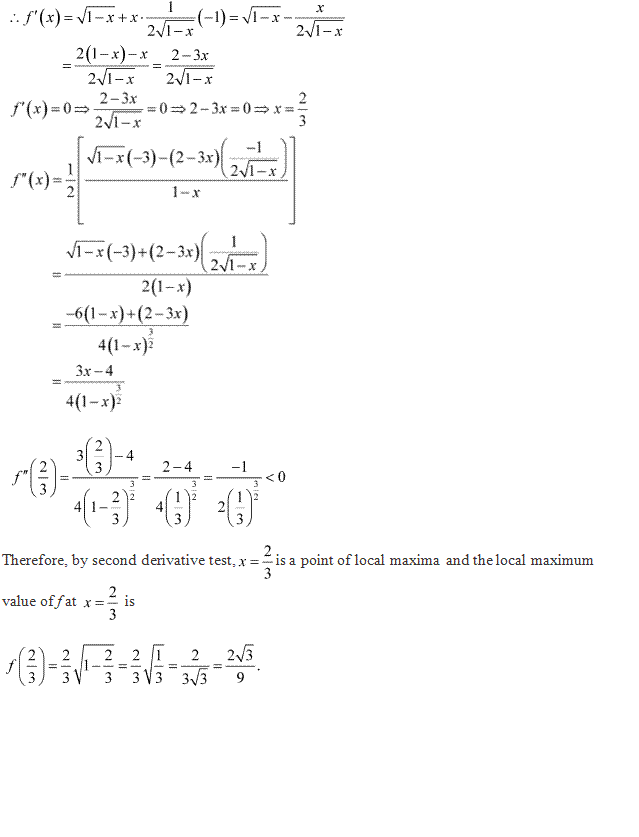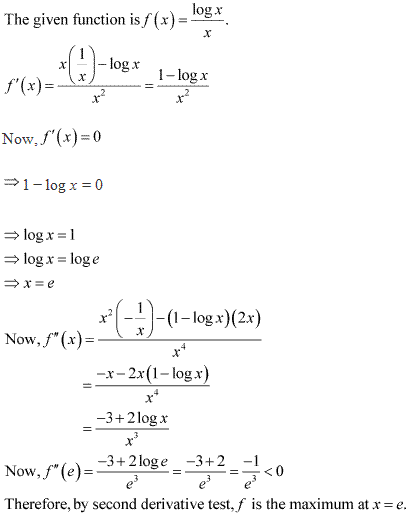Class 12-science RD SHARMA Solutions Maths Chapter 18 - Maxima and Minima
Maxima and Minima Exercise MCQ
Solution 30
Given: ![]() is defined as f(x) = 2x + cos
x
is defined as f(x) = 2x + cos
x
Differentiating w.r.t x, we get
f'(x) = 2 - sin x
As -sin x ≥ -1
Therefore, 1 - sin x > 0 for all x.
Hence, f(x) is an increasing function.
Solution 31
Let ![]()
Differentiating w.r.t x, we get
f'(x) = 2x - 8
Take f'(x) = 0, we get
2x - 8 = 0
i.e. x = 4
Again differentiating, we get
f"(x) = 2 > 0 for all real x
Therefore, x = 4 is the point of minima.
The minimum value of f(x) is
f(4) = 16 - 32 + 17 = 1
Solution 32
Let ![]()
Differentiating w.r.t x, we get
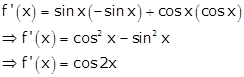
Take f'(x) = 0, we get
cos 2x = 0
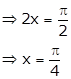
Again differentiating, we get
![]()
At ![]()
![]()
Therefore, ![]() is the point of
maxima.
is the point of
maxima.
The maximum value of f(x) is
![]()
Solution 33
Let ![]()
Taking log on both the sides, we get
![]() … (i)
… (i)
Differentiating w.r.t x, we get
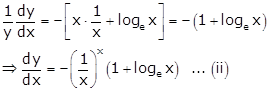
Differentiating w.r.t x, we get
![]() … (iii)
… (iii)
From equation (ii), we get
![]()
Take ![]() we get
we get
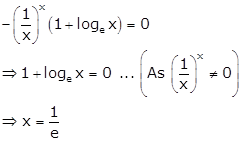
At ![]() we have
we have
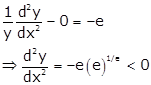
Therefore, ![]() is the point of
maxima.
is the point of
maxima.
The maximum value of f(x) is
![]()
Solution 34
Let ![]()
Taking log on both the sides, we get
![]() … (i)
… (i)
Differentiating w.r.t x, we get
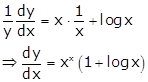
Take ![]() we get
we get
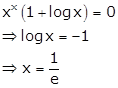
Thus, ![]() is the
stationary point.
is the
stationary point.
Solution 35
Given: ![]()
Differentiating w.r.t x, we get
![]() which is the
slope of the curve
which is the
slope of the curve
Differentiating ![]() w.r.t x, we
get
w.r.t x, we
get
![]()
Take ![]()
![]()
Again differentiating w.r.t x, we get
![]()
So, the slope is maximum at x = 1
![]()
Solution 36
Given: ![]()
Differentiating w.r.t x, we get
![]()
Take f'(x) = 0, we get
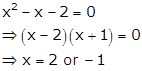
Now, let's find f(x) at x = 2 or -1

Therefore, x = -1 is the point of local maxima and the maximum value is 11.
Whereas, x = 2 is the point of local minima and the minimum value is -16.
Hence, f(x) has one maximum and one minimum.
Solution 1
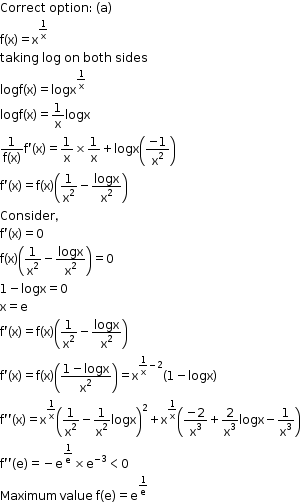
Solution 2
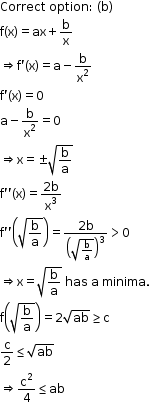
Solution 3
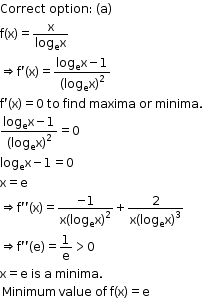
Solution 4
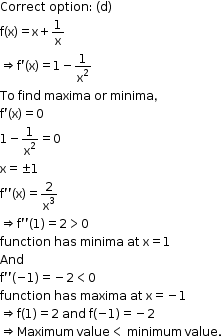
Solution 5
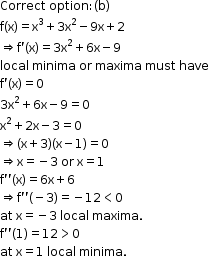
Solution 6
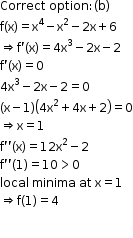
Solution 7
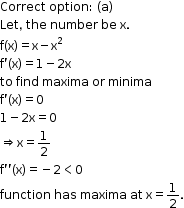
Solution 8

Solution 9

Solution 10

Solution 11
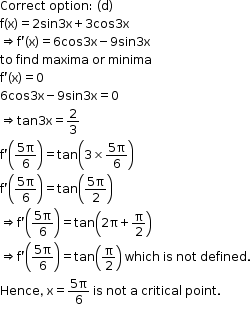
Solution 12

Solution 13

Solution 14

Solution 15
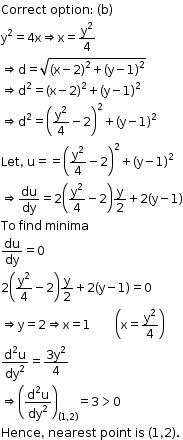
Solution 16

Solution 17

Solution 18

Solution 19
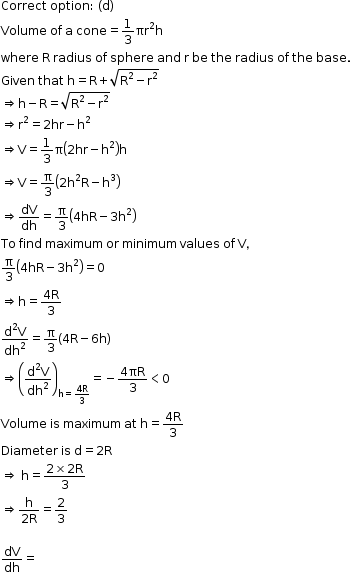
Solution 20

Solution 21

Solution 22

Solution 23
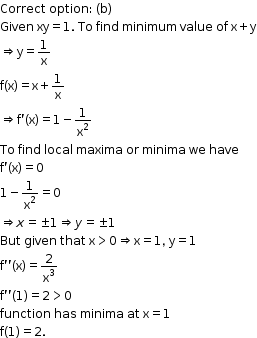
Solution 24
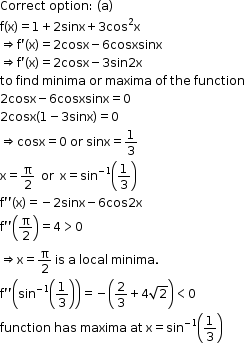
Solution 25

Solution 26
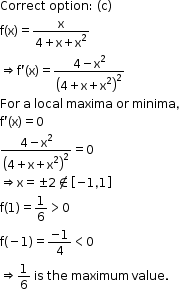
Solution 27

Solution 28
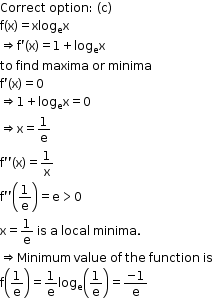
Solution 29
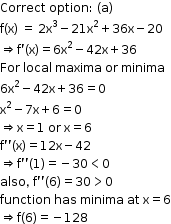
Maxima and Minima Exercise Ex. 18.1
Solution 1
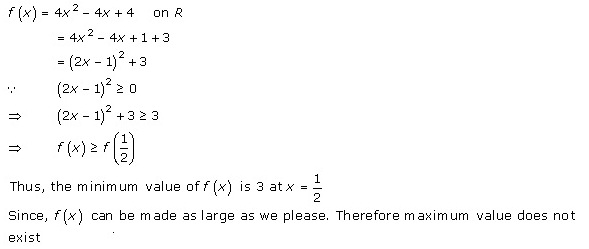
Solution 2

Solution 3

Solution 4
Solution 5
Solution 6

Solution 7
Solution 8

Solution 9

Maxima and Minima Exercise Ex. 18.2
Solution 1

Solution 2

Solution 3
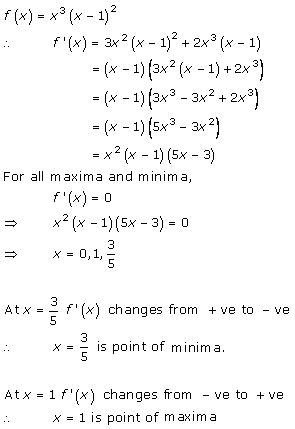
Solution 4

Solution 5
Solution 6

Solution 7

Solution 8
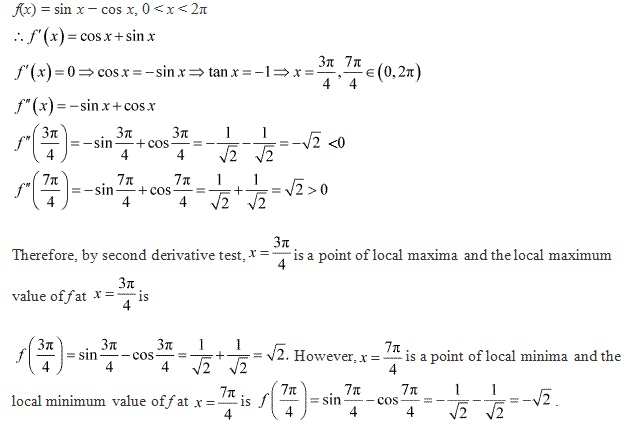
Solution 9

Solution 10
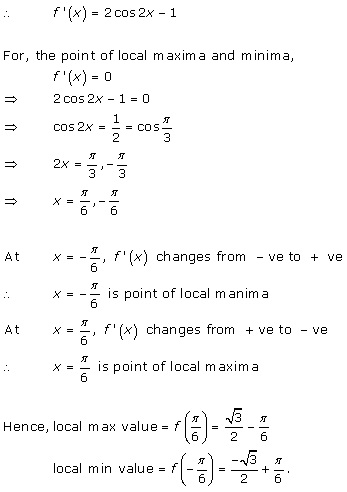
Solution 11
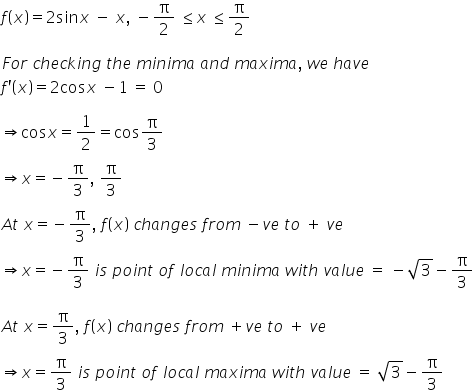
Solution 12
Solution 13
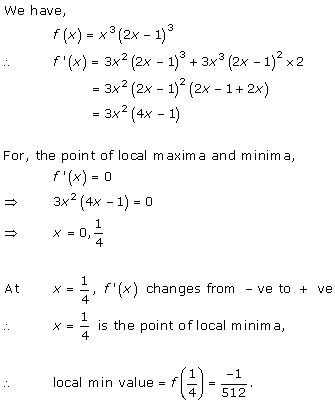
Solution 14

Maxima and Minima Exercise Ex. 18.3
Solution 1(i)

Solution 1(ii)

Solution 1(iii)
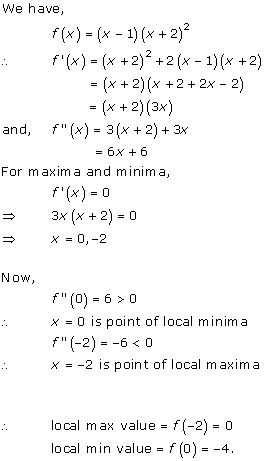
Solution 1(iv)
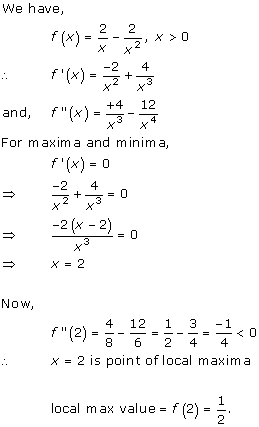
Solution 1(v)

Solution 1(vi)
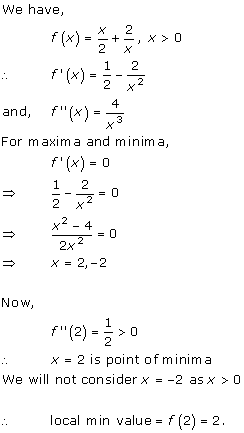
Solution 1(vii)
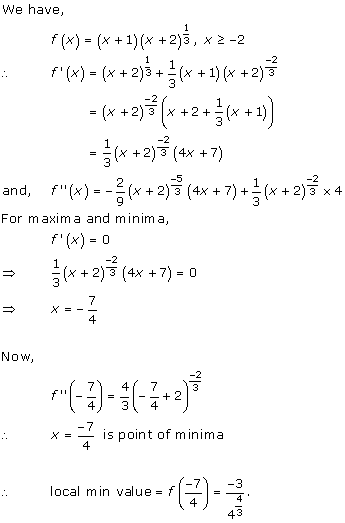
Solution 1(viii)

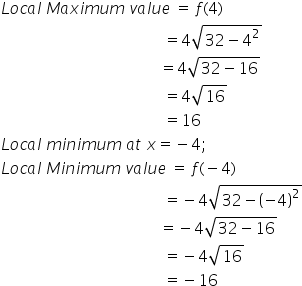
Solution 1(ix)

Solution 1(x)
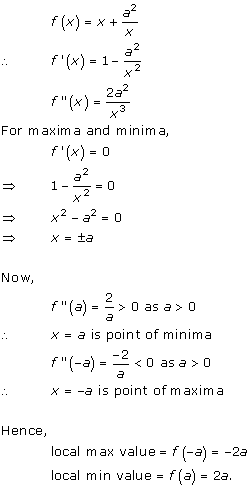
Solution 1(xi)

Solution 1(xii)

Solution 2(i)
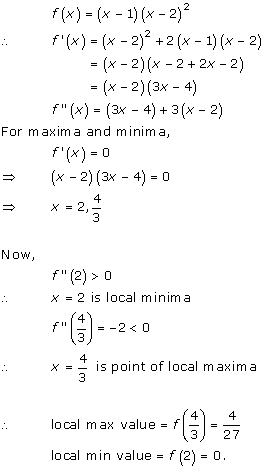
Solution 2(ii)
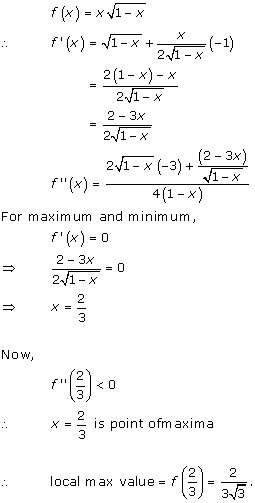
Solution 2(iii)
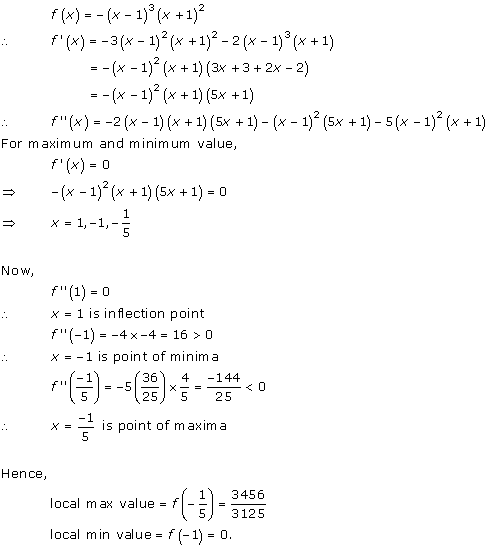
Solution 3
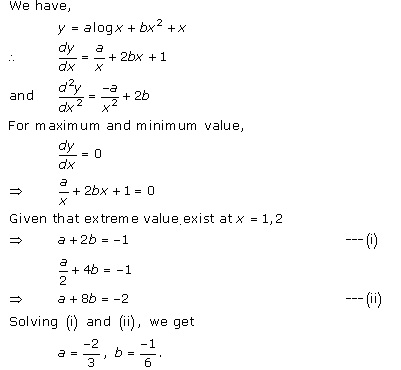
Solution 4
Solution 5
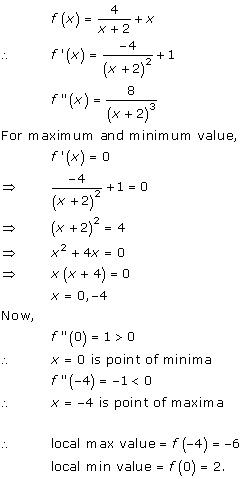
Solution 6
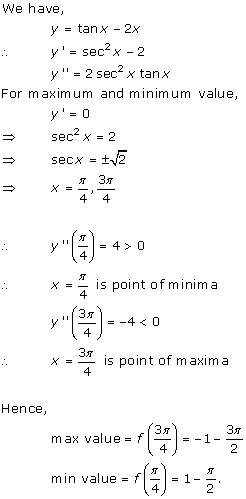
Solution 7

Solution 8
Given: ![]()
Differentiating w.r.t x, we get
![]()
Take f'(x) = 0
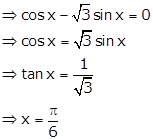
Differentiating f'(x) w.r.t x, we get
![]()
At ![]()
![]()
Clearly, f"(x)
< 0 at ![]()
Thus, ![]() is the maxima.
is the maxima.
Hence, f(x) has
maximum value at ![]() .
.
Maxima and Minima Exercise Ex. 18.4
Solution 1(i)

Solution 1(ii)

Solution 1(iii)
Solution 1(iv)
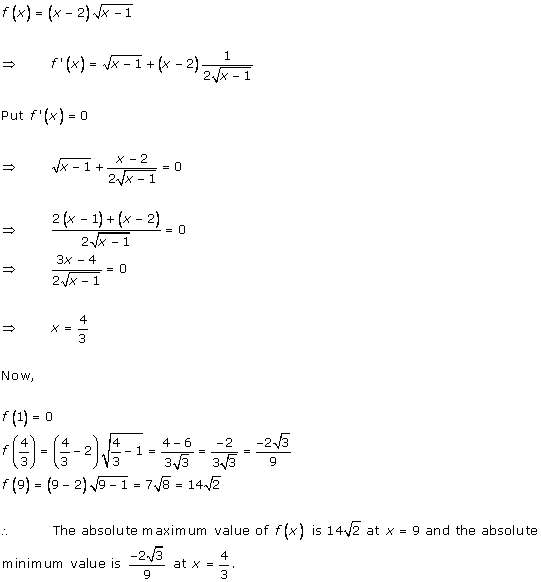
Solution 2

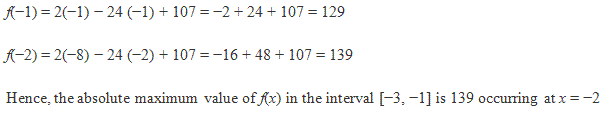
Solution 3

Solution 4
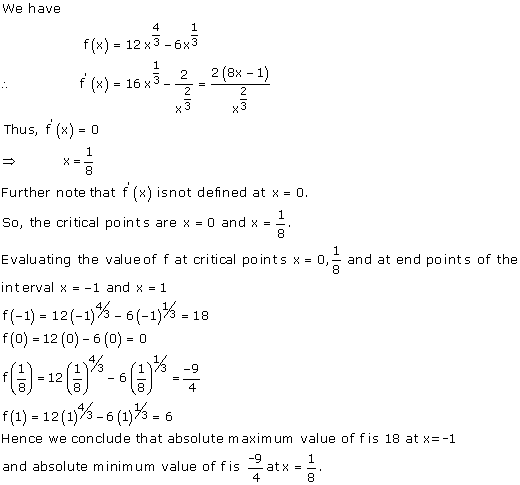
Solution 5

Maxima and Minima Exercise Ex. 18.5
Solution 1
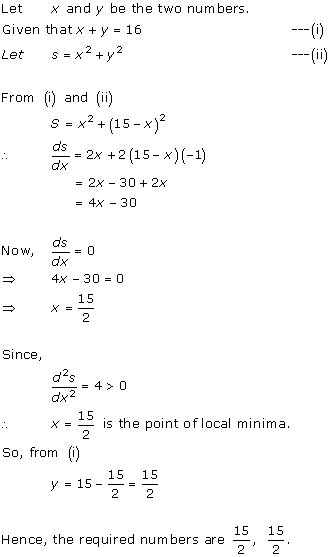
Solution 2

Solution 3

Solution 4

Solution 6

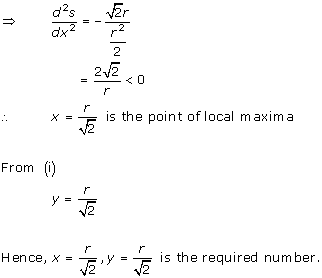
Solution 7
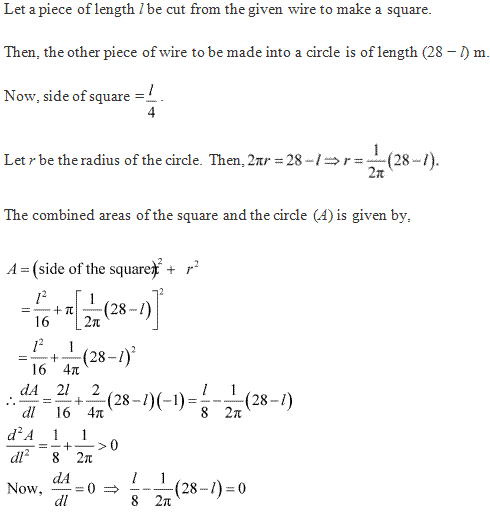
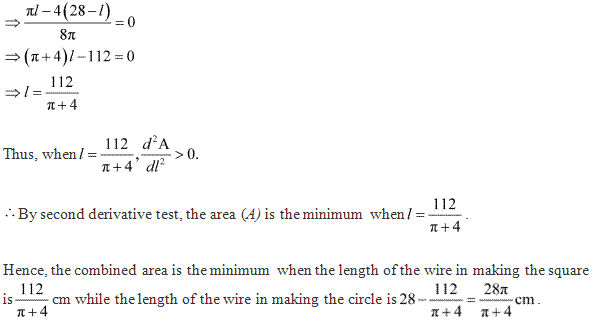
Solution 8
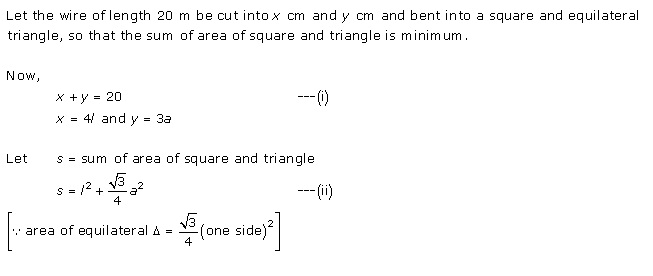

Solution 9
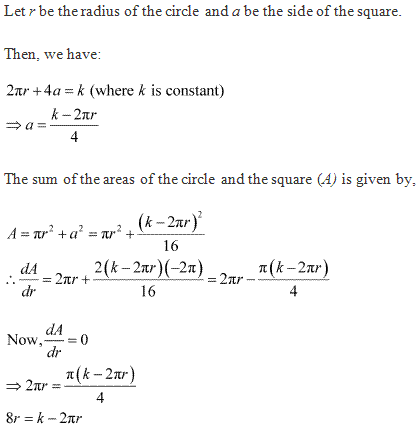

Solution 10

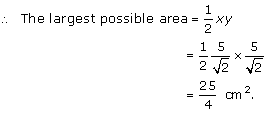
Solution 11

Solution 12

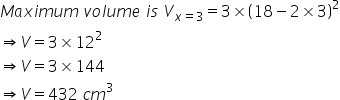
Solution 13
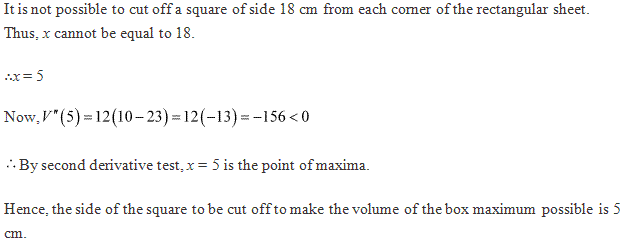
Solution 14
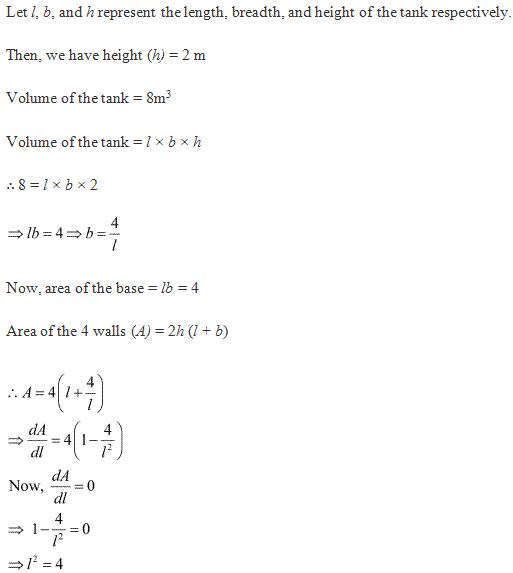
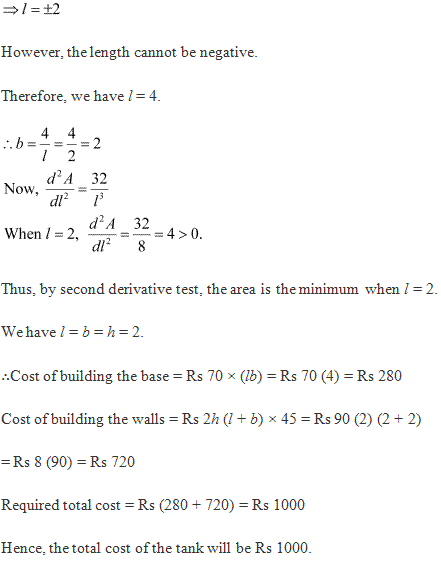
Solution 15


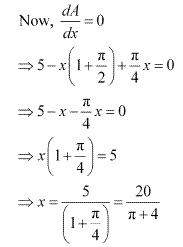

Solution 16

Solution 17
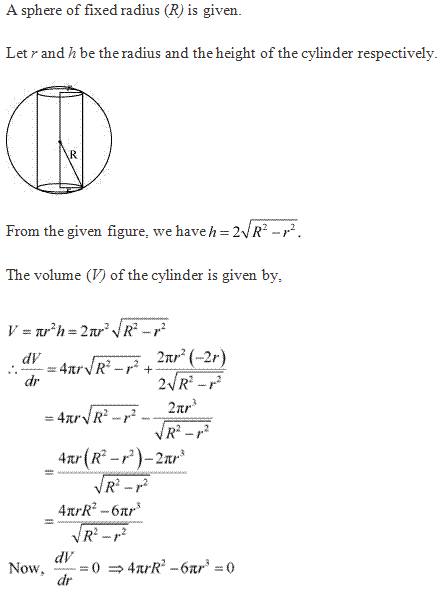

Solution 18


Solution 19
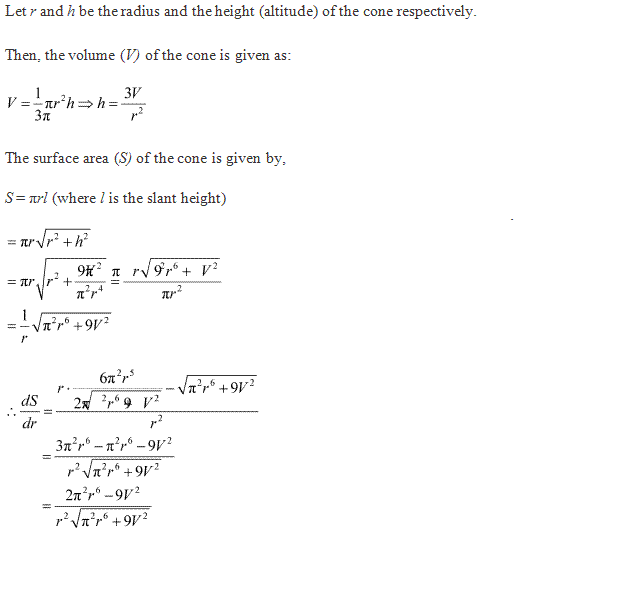
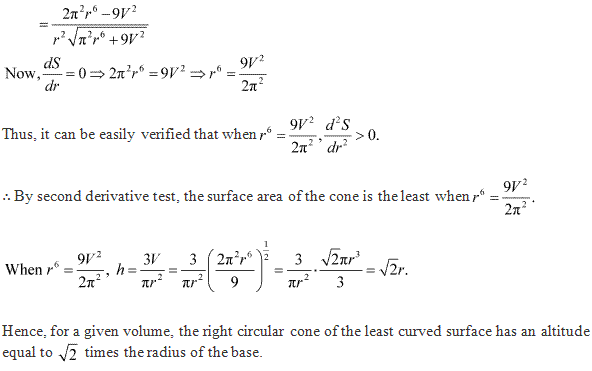
Solution 20
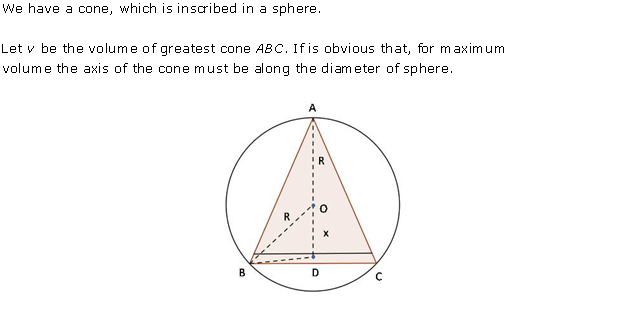

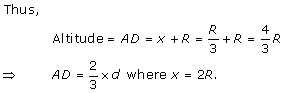
Solution 21

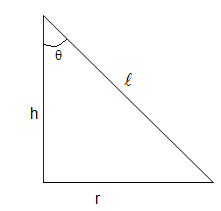

Solution 22



Solution 24

Solution 25
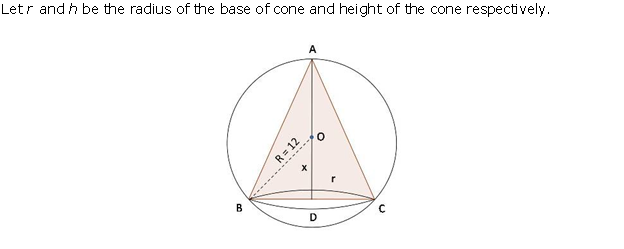

Solution 26

Solution 27
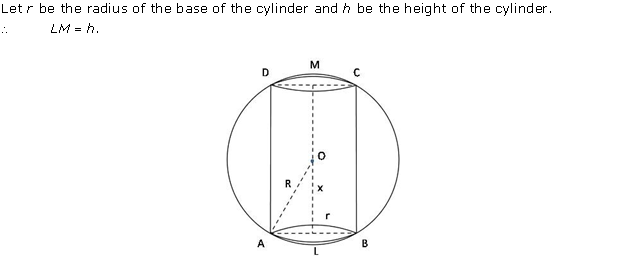

Solution 28
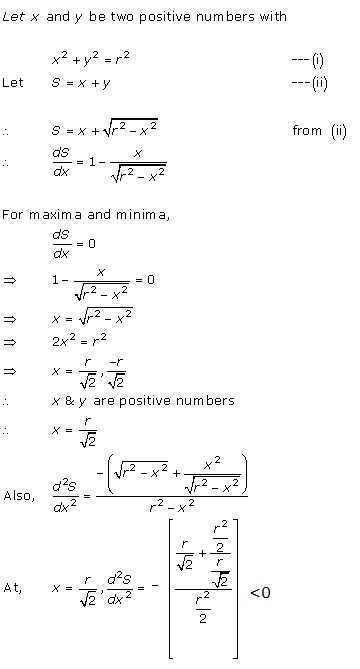

Solution 29

Solution 30
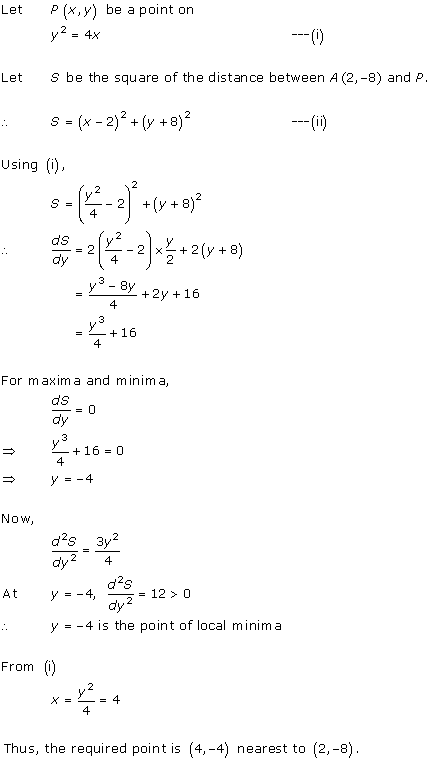
Solution 31

Solution 32
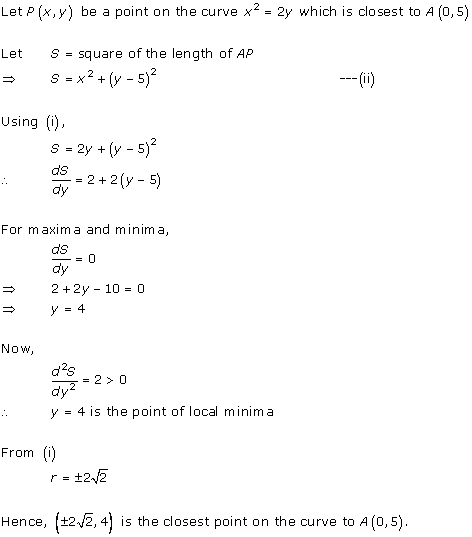
Solution 33

Solution 34

Solution 35
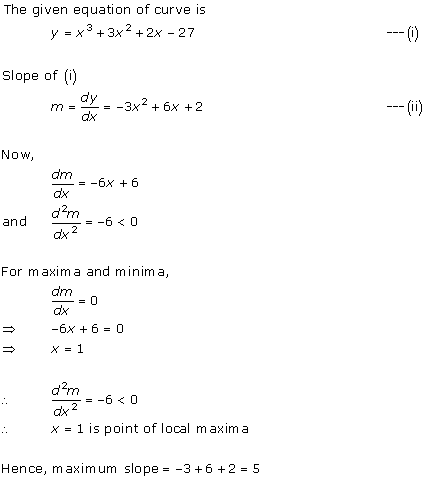
Solution 36

Solution 37

Solution 38

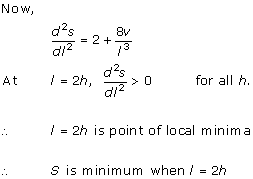
Solution 39
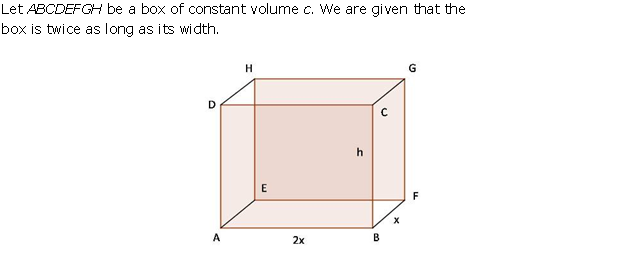

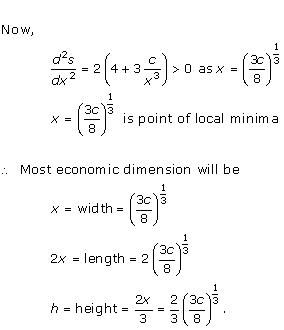
Solution 40

Solution 41

Solution 42
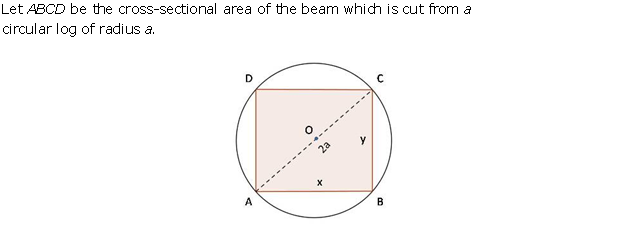

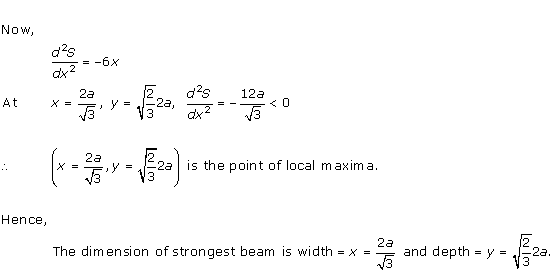
Solution 43

Solution 44



Solution 45

Solution 45
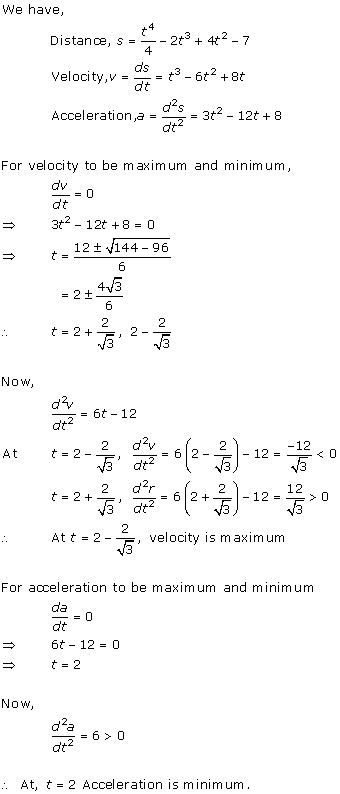
Solution 5
Let r and h be the radius and height of the cylinder.
Volume of
cylinder ![]()
![]() … (i)
… (i)
Surface area of
cylinder ![]()
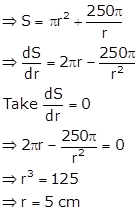
From (i), we get
![]()
Solution 23
Let ![]() be an
isosceles triangle with AB = AC.
be an
isosceles triangle with AB = AC.
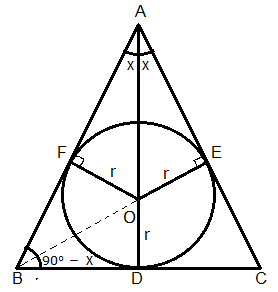
Let ![]()
Here, AO bisects ![]()
Taking O as the centre of the circle, join OE, OF and OD such that
OE = OF = OD = r (radius)
Now, ![]()
In ![]()
![]()
Similarly, AF = r cot x
In ![]()
![]()
As OB bisect ![]() we have
we have
![]()
In ![]()
Similarly, BD =
DC = CE = ![]()
We have,
perimeter of ![]()
P = AB + BC + CA
= AE + EC + BD + DC + AF + BF
![]()
Differentiating w.r.t x, we get
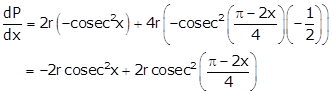
Taking ![]()
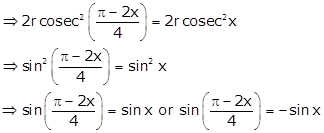
As ![]()
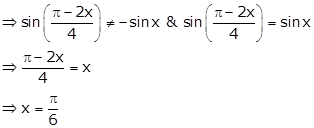
Therefore, ![]() is an
equilateral triangle.
is an
equilateral triangle.
Taking second derivative of P, we get
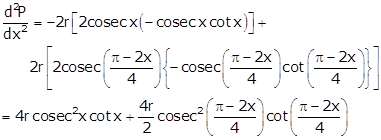
At ![]()
Therefore, the
perimeter is minimum when ![]()
Least value of P 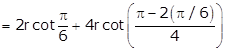
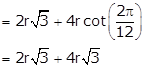
![]()
Maxima and Minima Exercise Ex. 18VSAQ
Solution 1
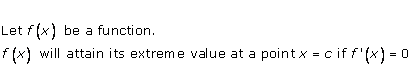
Solution 2

Solution 3
![]()
Solution 4
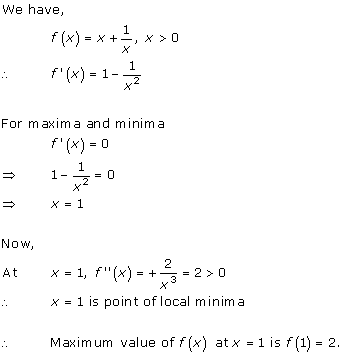
Solution 5
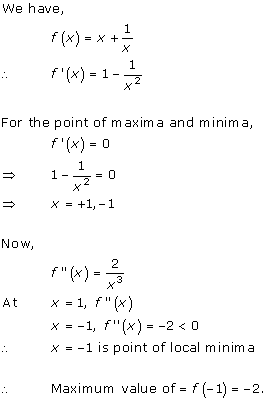
Solution 6
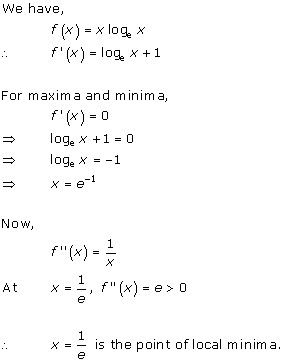

Solution 7
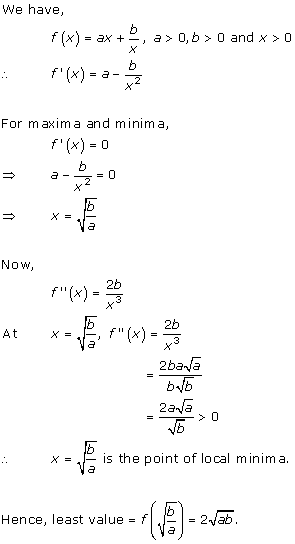
Solution 8

Solution 9
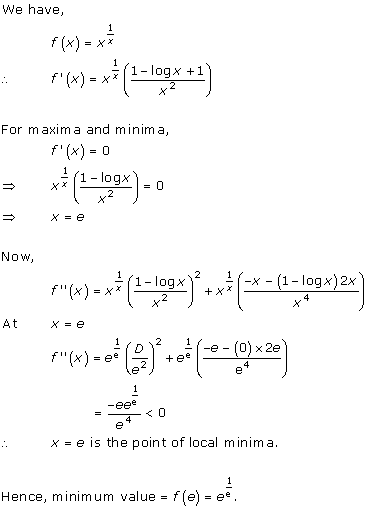
Solution 10