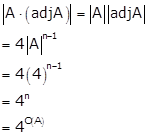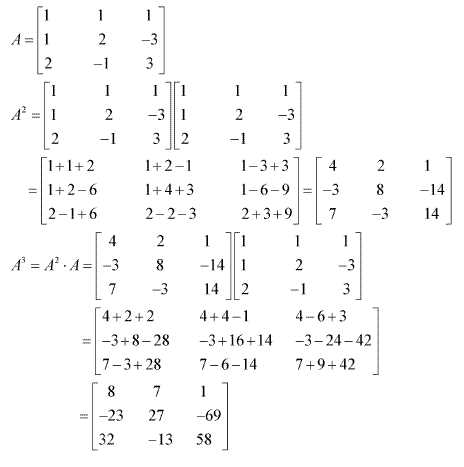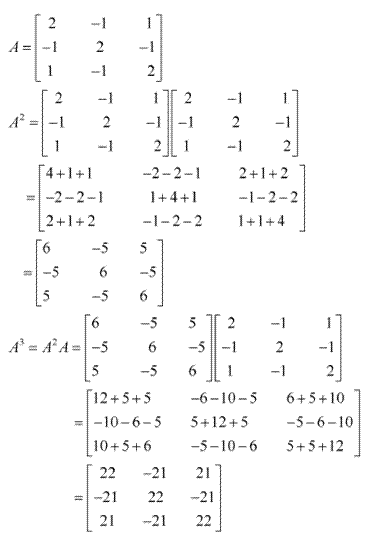Class 12-science RD SHARMA Solutions Maths Chapter 7 - Adjoint and Inverse of a Matrix
Adjoint and Inverse of a Matrix Exercise Ex. 7.1
Solution 1(i)

Solution 1(ii)

Solution 1(iii)

![]()
Solution 1(iv)


Solution 2(i)

Solution 2(ii)

Solution 2(iii)

Solution 2(iv)

Solution 3

Solution 4

Solution 5
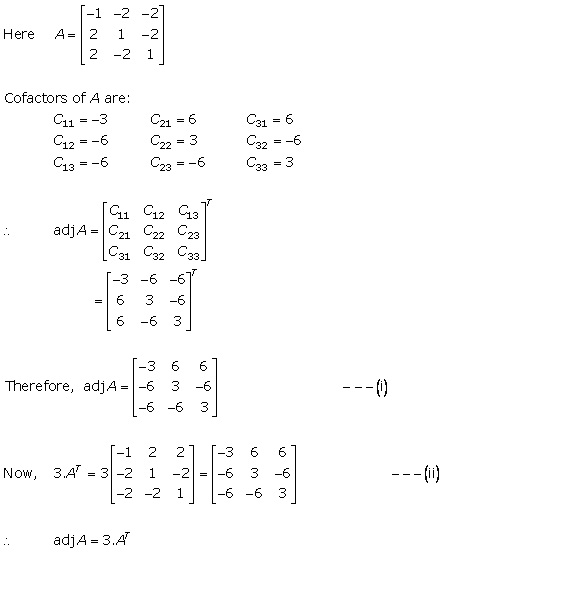
Solution 6

Solution 7(i)

Solution 7(ii)
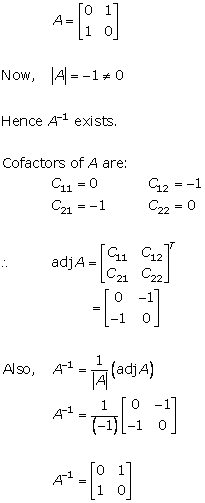
Solution 7(iii)
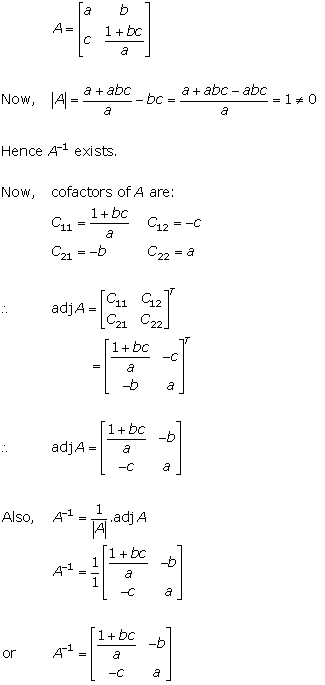
Solution 7(iv)
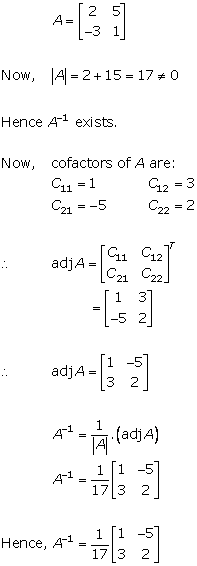
Solution 8(i)

Solution 8(ii)

Solution 8(iii)
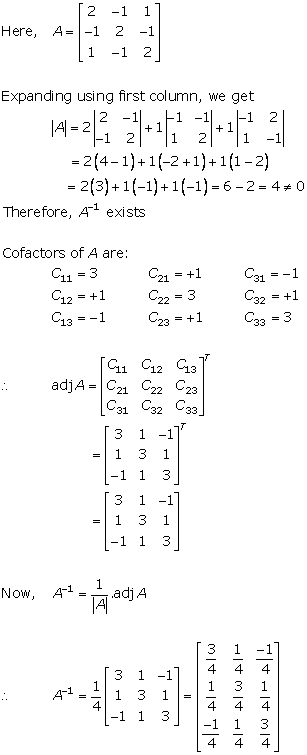
Solution 8(iv)

Solution 8(v)
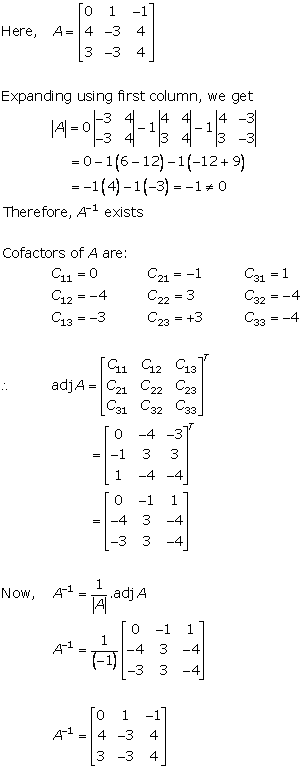
Solution 8(vi)
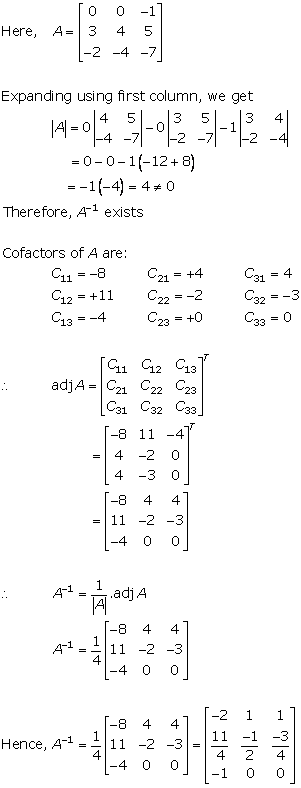
Solution 8(vii)
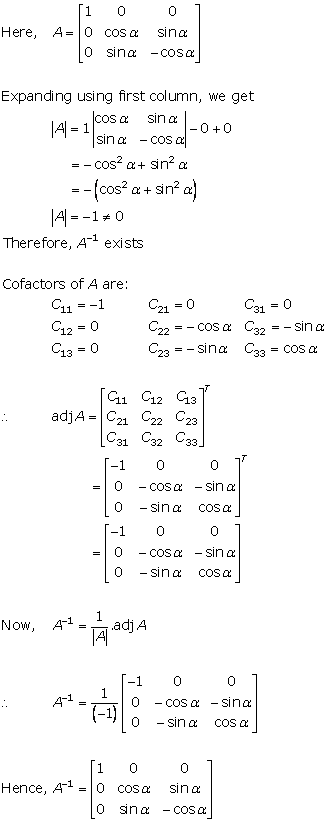
Solution 9(i)
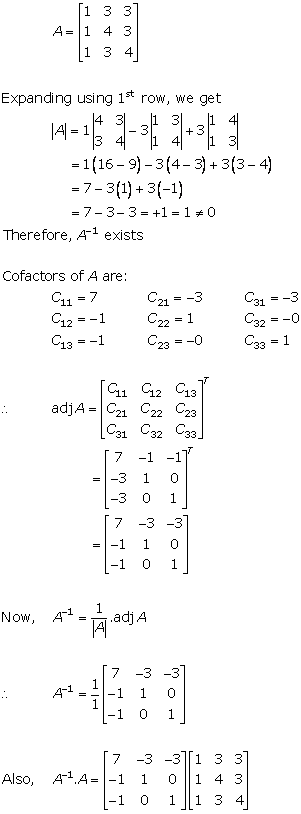
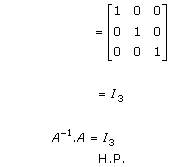
Solution 9(ii)
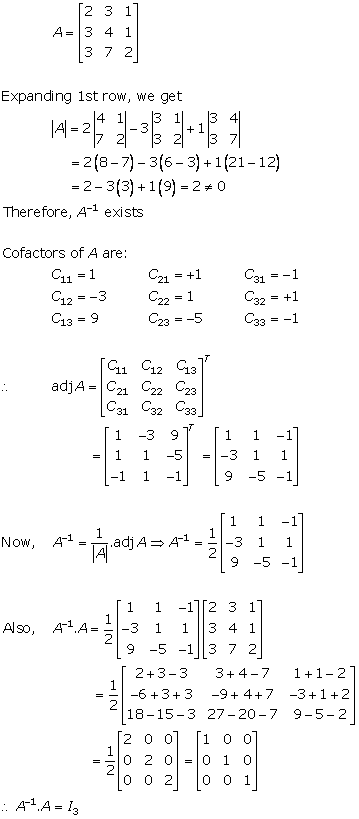
Solution 10(i)
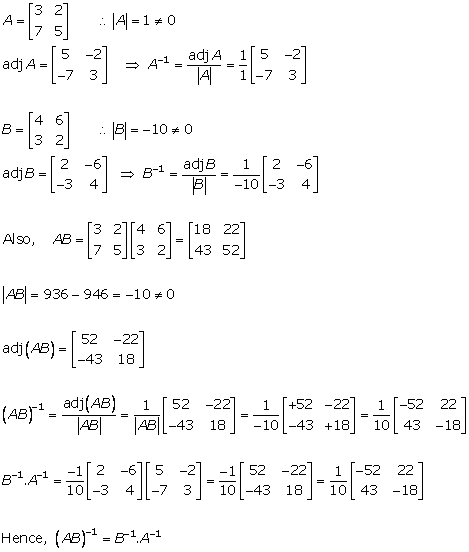
Solution 10(ii)

Solution 11

Solution 12
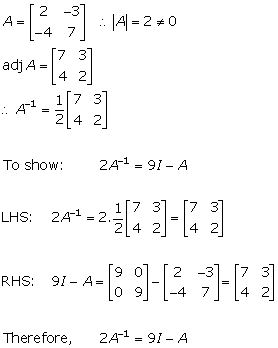
Solution 13

Solution 14

Solution 15
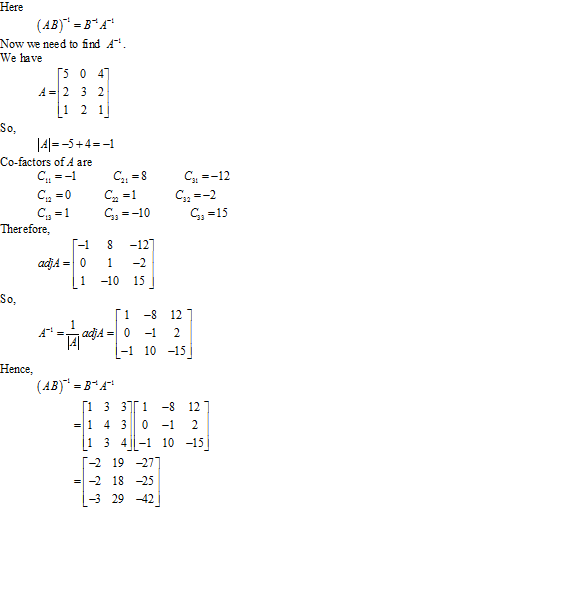
Solution 16(i)

Solution 16(ii)

Solution 16(iii)
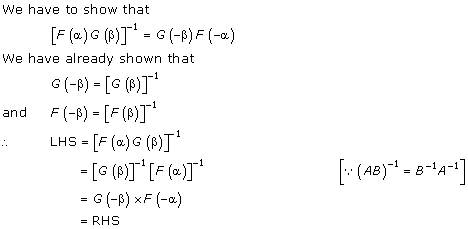
Solution 17
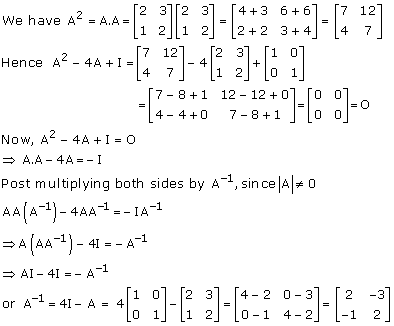
Solution 18

Solution 19

Solution 20

Solution 21

Solution 22

Solution 23
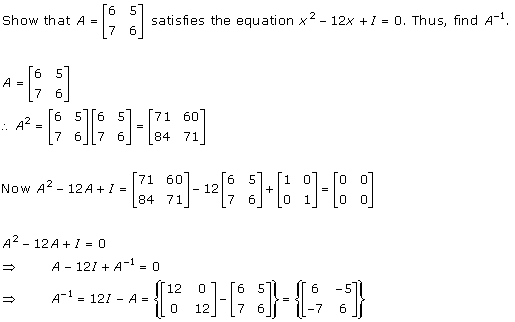
Solution 24


Solution 25

Solution 26

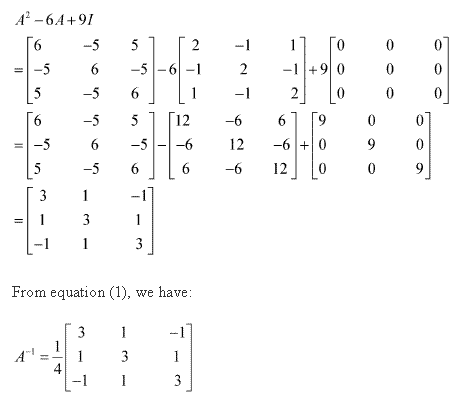
Solution 27

Solution 28

Solution 29

Solution 30
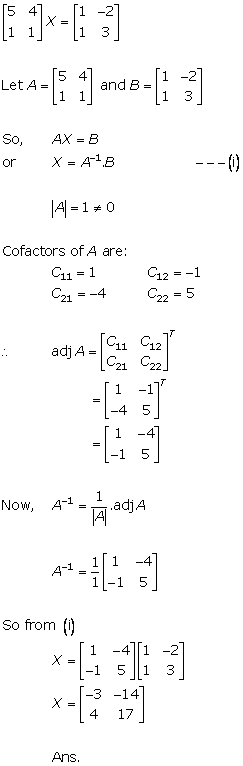
Solution 31
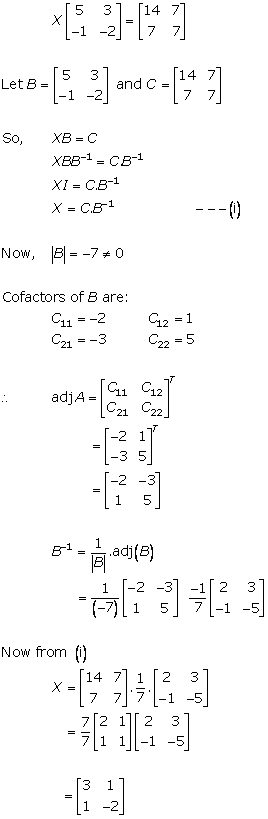
Solution 32

Solution 33

Solution 34
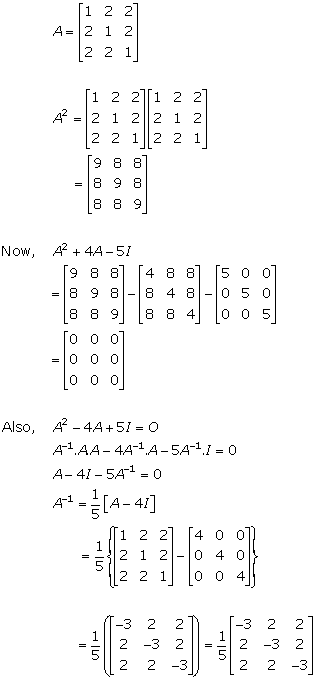
Solution 35

Solution 36

Solution 37
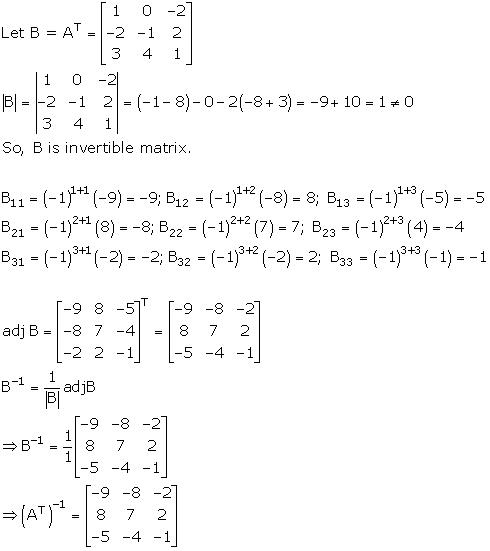
Solution 38
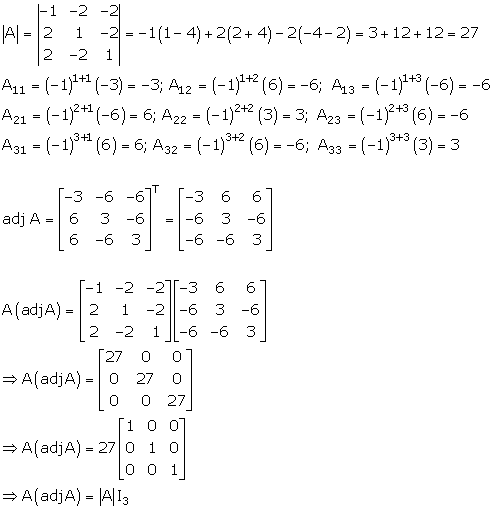
Solution 39
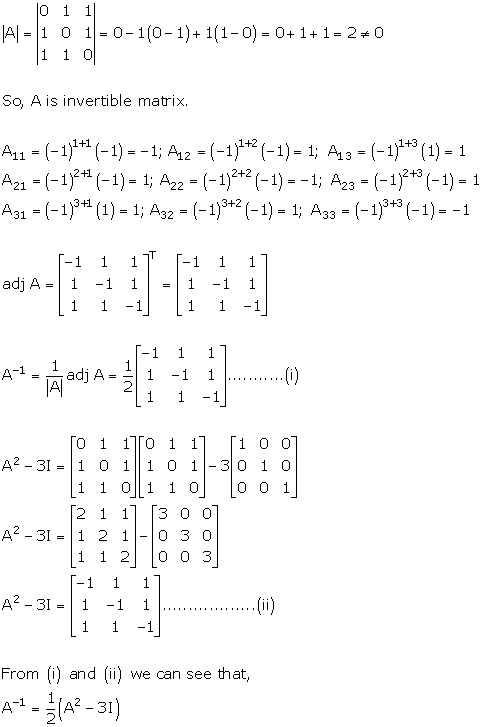
Adjoint and Inverse of a Matrix Exercise Ex. 7.2
Solution 1
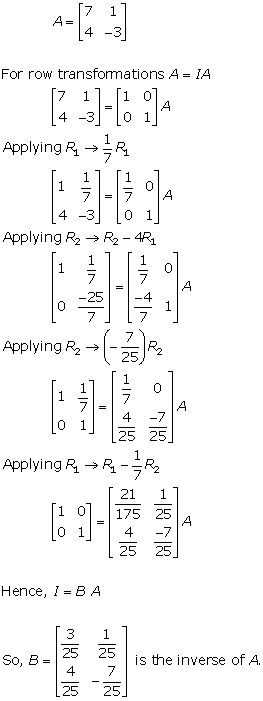
Solution 2

Solution 3
Let ![]()
AA-1 = I
![]()
Applying R2→ R2 - 2R1
![]()
Applying R2→ R2/-5

Applying R1→ R1 - 2R2
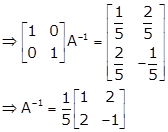
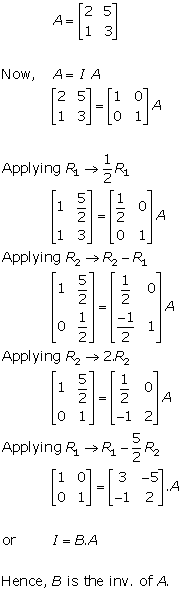
Solution 4
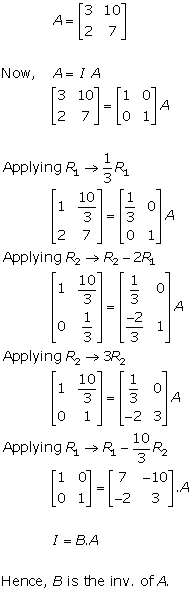
Solution 5
Solution 6

Solution 7

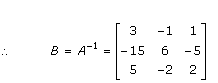
Solution 8
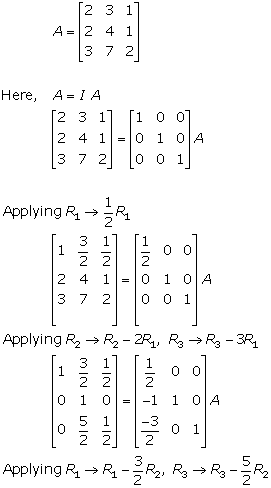

Solution 9

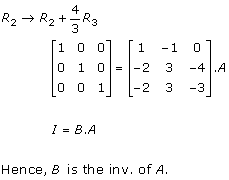
Solution 10

Solution 11

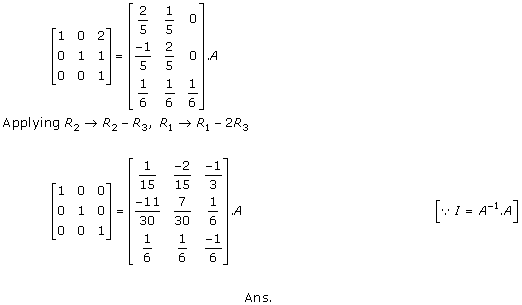
Solution 12

![]()
Solution 13

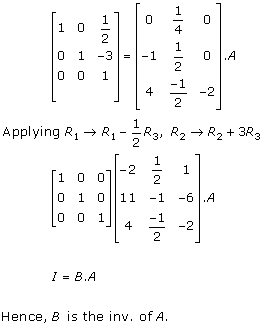
Solution 14
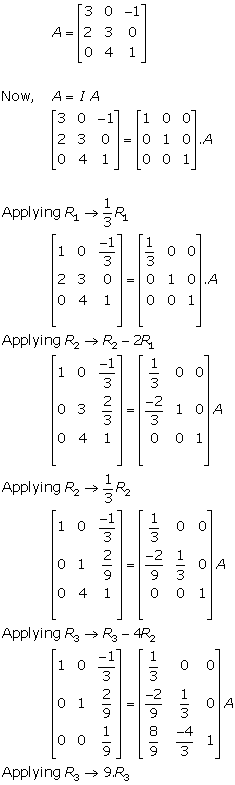
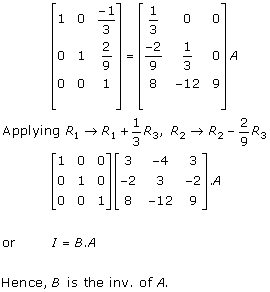
Solution 15
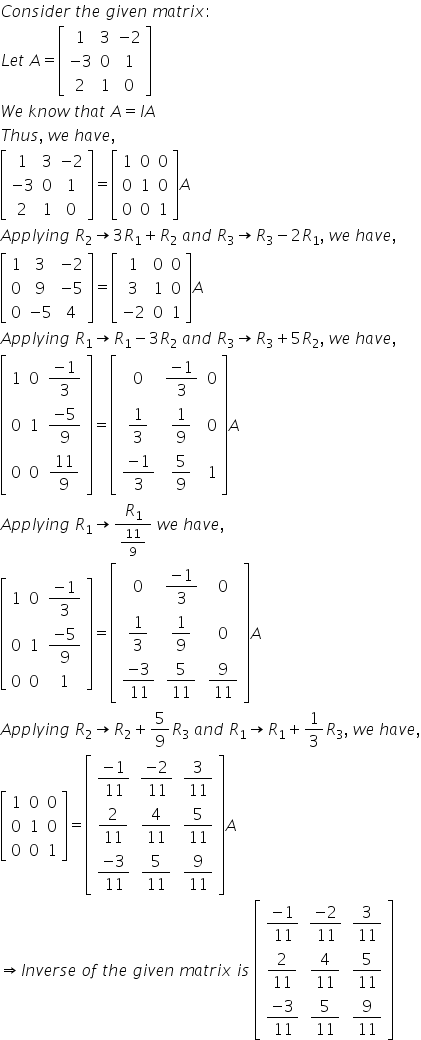
Solution 16
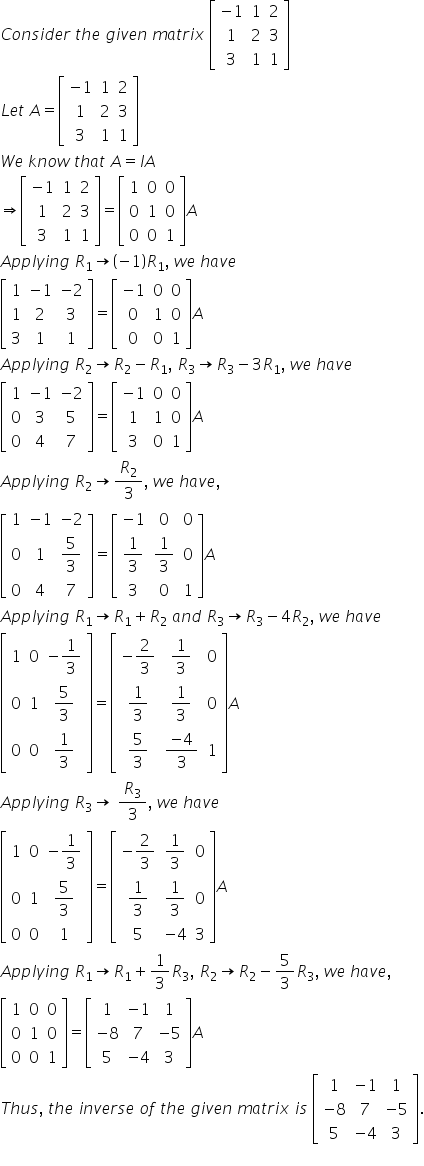
Solution 17
Let 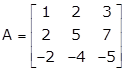
AA-1 = I
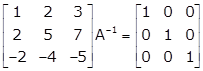
Applying R2→ R2 - 2R1 and R3→ R3 + 2R1

Applying R1→ R1 - 2R2
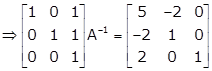
Applying R1→ R1 - R3 and R2→ R2 - R3

Hence, 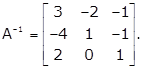
Solution 18
Let 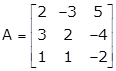
AA-1 = I
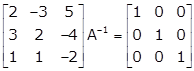
Applying R3 ↔ R1
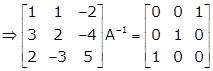
Applying R2→ R2 - 3R1 and R3→ R3 - 2R1
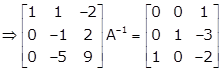
Applying R2→ -R2

Applying R1→ R1 - R2 and R3→ R3 + 5R2

Applying R3→ -R3
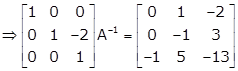
Applying R2→ R2 + 2R3

Hence, 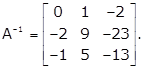
Adjoint and Inverse of a Matrix Exercise MCQ
Solution 1
Correct option: (a)
|A-1| = |A|-1, (AT)-1 = (A-1)T, |A| ≠ 0 are properties of an invertible matrix.
Solution 2
Correct option: (c)
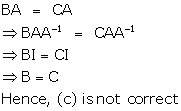
Solution 3
Correct option:(d)
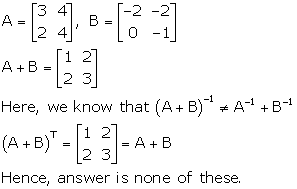
Solution 4
Correct option: (b)
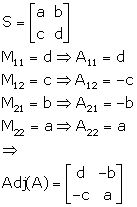
Solution 5
Correct option:(b)
If A is singular matrix then adjoint of A is also singular.
Solution 6
Correct option: (a)

Solution 7
Correct option: (c)
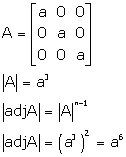
Solution 8
Correct option:(a)
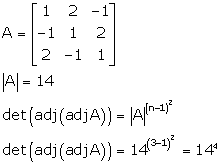
Solution 9
Correct option: (c)
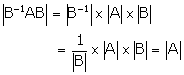
Solution 10
Correct option: (c)
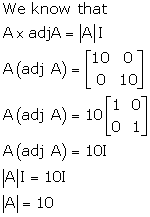
Solution 11
Correct option: (d)
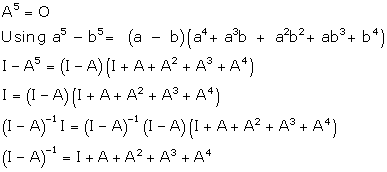
Solution 12
Correct option: (d)
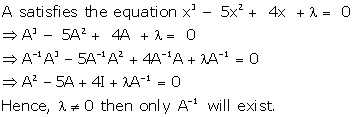
Solution 13
Correct option: (a)
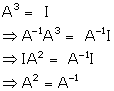
Solution 14
Correct option: (b)

Solution 15
Correct option: (c)
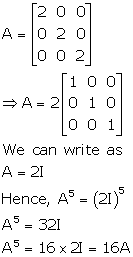
Solution 16
Correct option: (d)
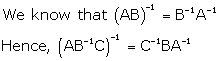
Solution 17
Correct option: (d)
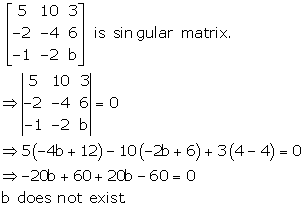
Solution 18
Correct option: (b)
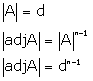
Solution 19
Correct option: (d)
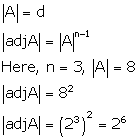
Solution 20
Correct option: (c)
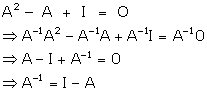
Solution 21
Correct option: (c)
Adj A = |A| A-1, Det(A-1) = (det A)-1, (AB)-1 = B-1A-1 are all the properties of invertible matrix.
Solution 22
Correct option: (b)
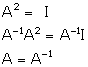
Solution 23
Correct option: (a)
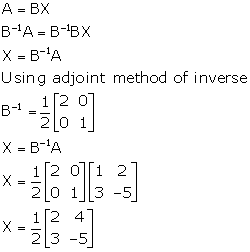
Solution 24
Correct option: (b)
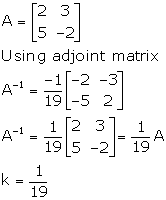
Solution 25
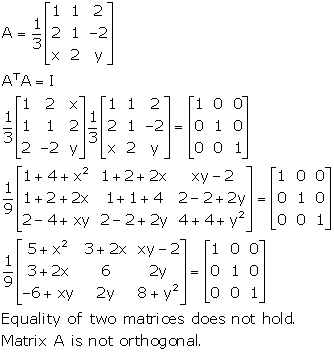
Solution 26
Correct option: (d)
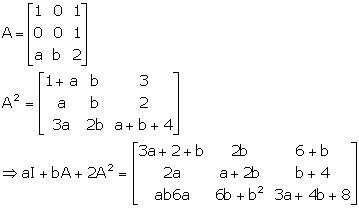
Solution 27
Correct option: (b)

Solution 28
Correct option: (d)

Solution 29
Correct option: (b)
![]()
Solution 30
Correct option: (a)
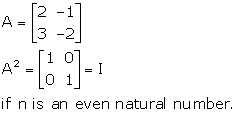
Solution 31
Correct option: (a)
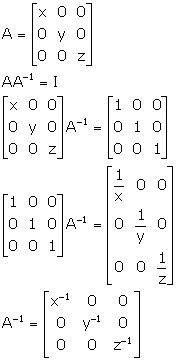
Solution 32
Given: A and B are invertible matrices
Relation between inverse and adjoint of a matrix is given by

We know that, AA-1 = I
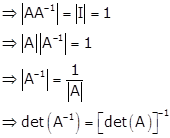
As ![]()
![]()
But ![]()
![]()
Solution 33
A matrix is invertible or its inverse exists if determinant is 0.
Now, ![]()
Therefore, A-1 exists if |A| = 0
i.e. if ![]()
i.e. if ![]()
Solution 34
Given: A2 = A
(I - A)3 + A = (I - A)2(I - A) + A
= (I2 - 2AI + A2)(I - A) + A
= (I- 2A + A)(I - A) + A … (Since A2 = A)
= (I - A)(I - A) + A
= I2 - 2AI + A2 + A
= I - 2A + A + A
= I
Hence, (I - A)3 + A = I.
Solution 35
The matrix is non-invertible if its determinant is 0.
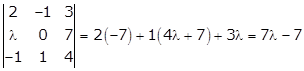
This matrix will not be invertible if ![]()
i.e. if ![]()
Adjoint AND Inverse of a Matrix Exercise Ex. 7VSAQ
Solution 1

Solution 2

Solution 3

Solution 4

Solution 5

Solution 6
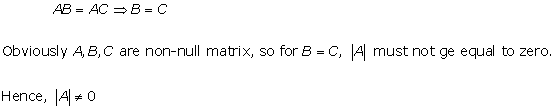
Solution 7
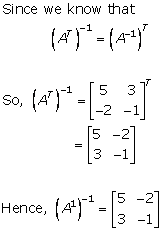
Solution 8
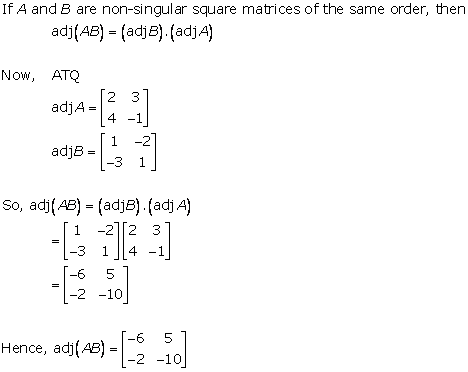
Solution 9

Solution 10

Solution 11

Solution 12
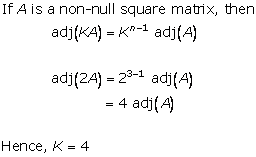
Solution 13
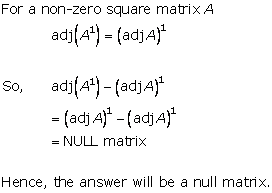
Solution 14

Solution 15
![]()
Solution 16
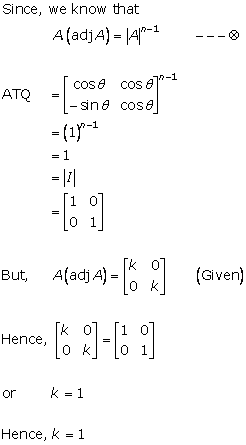
Solution 17
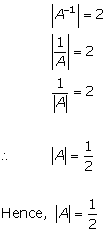
Solution 18

Solution 19
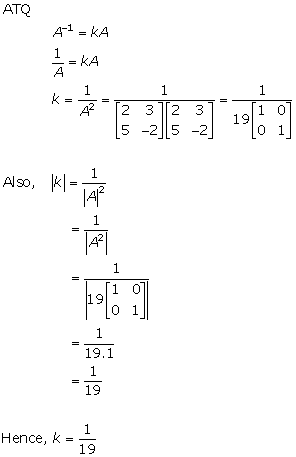
Solution 20

Solution 21
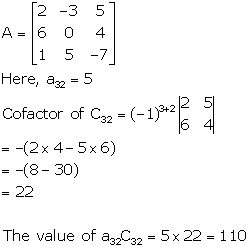
Solution 22
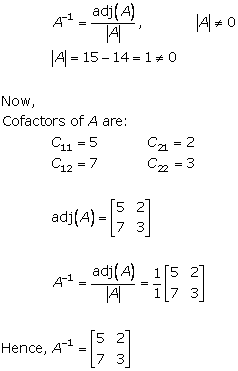
Solution 23
Solution 24
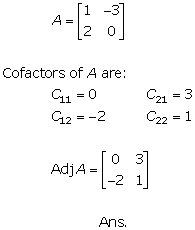
Solution 25

Solution 26

Solution 27
Solution 28

Solution 29
Given: ![]() which is in
the form X = AB
which is in
the form X = AB
Now, the column operation is applicable on X and B simultaneously when the equation is X = AB
Therefore, we'll apply the column operation on the first and third matrices.
Applying C2→ C2 + 2C1
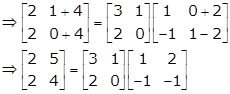
Solution 30
Given: ![]() which is in
the form AB = X
which is in
the form AB = X
Now, the row operation is applicable on A and X simultaneously when the equation is AB = X
Therefore, we'll apply the row operation on the first and third matrices.
Applying R2→ R2 + R1
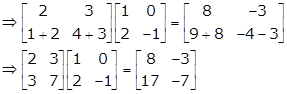
Solution 31
Given: |A| = 4