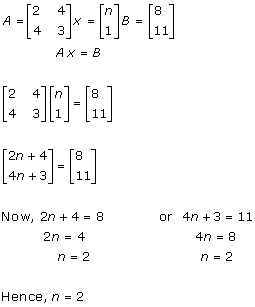Class 12-science RD SHARMA Solutions Maths Chapter 8 - Solution of Simultaneous Linear Equations
Solution of Simultaneous Linear Equations Exercise Ex. 8.1
Solution 1(i)

Solution 1(ii)

Solution 1(iii)
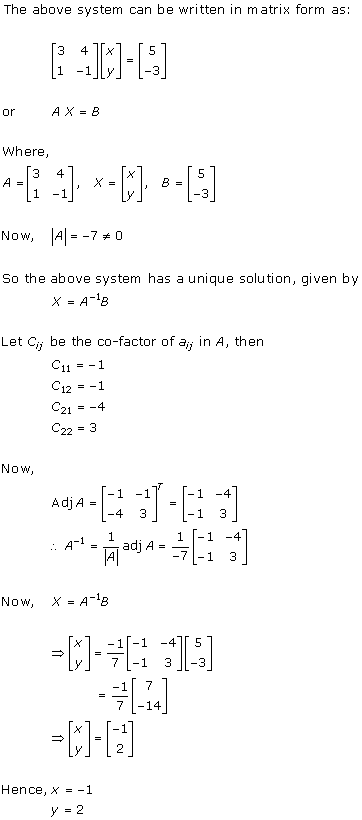
Solution 1(iv)

Solution 1(v)

Solution 1(vi)

Solution 2(i)

Solution 2(ii)

Solution 2(iii)

Solution 2(iv)

Solution 2(v)
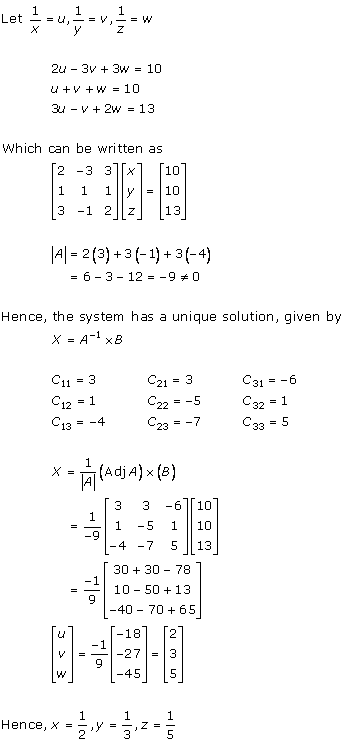
Solution 2(vi)

Solution 2(vii)

Solution 2(viii)

Solution 2(ix)

Solution 2(x)

Solution 2(xi)

Solution 2(xii)
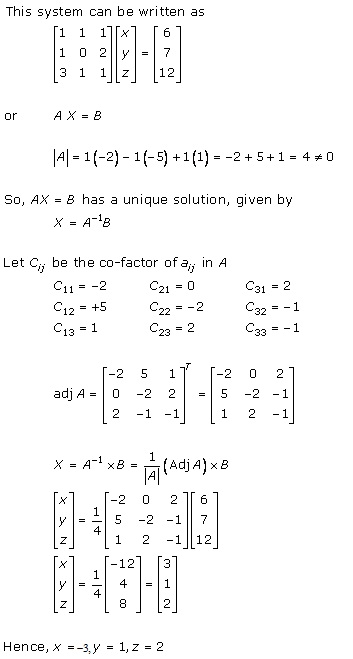
Solution 2(xiii)
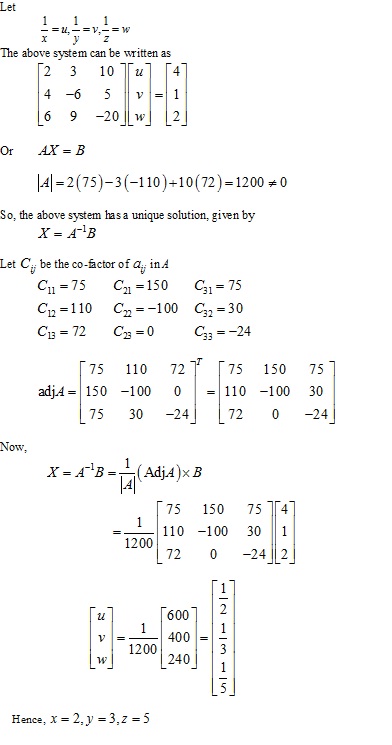
Solution 2(xiv)

Solution 3(i)

Solution 3(ii)

Solution 3(iii)
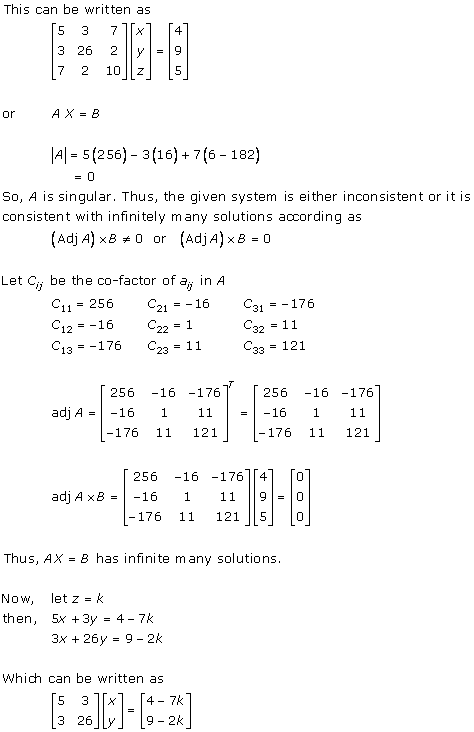

Solution 3(iv)
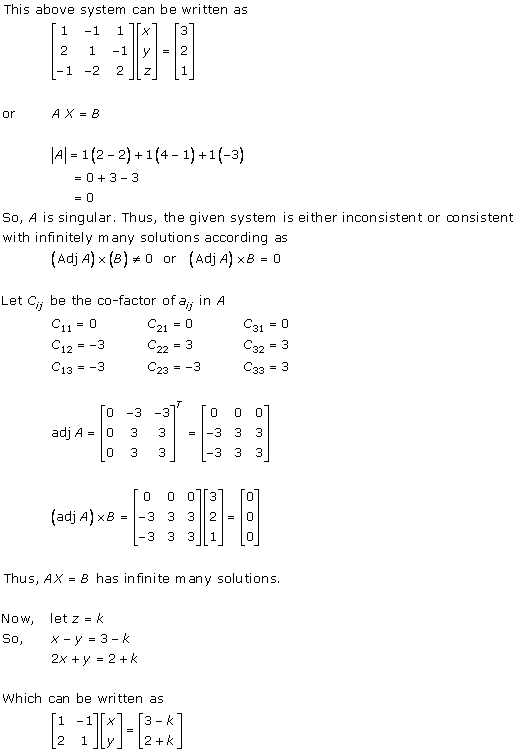
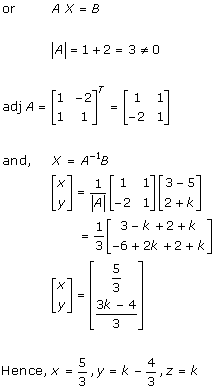
Solution 3(v)

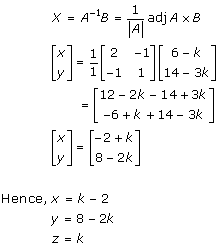
Solution 3(vi)

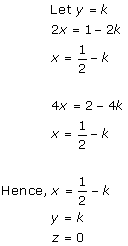
Solution 4(i)

Solution 4(ii)
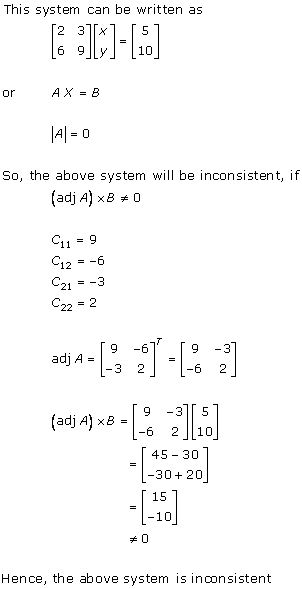
Solution 4(iii)
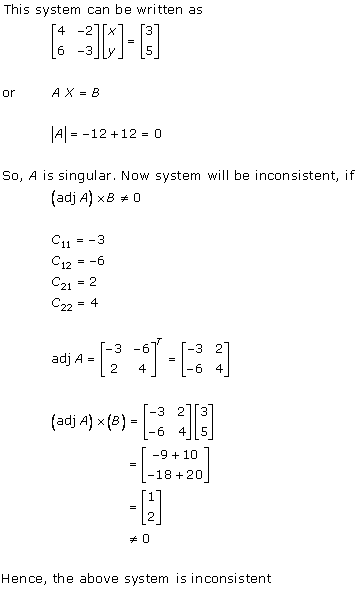
Solution 4(iv)

Solution 4(v)
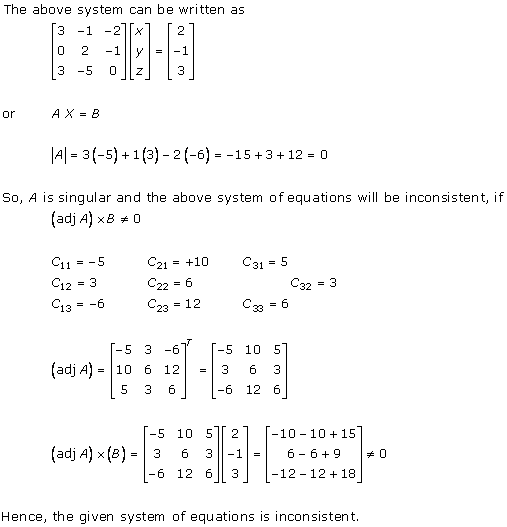
Solution 4(vi)
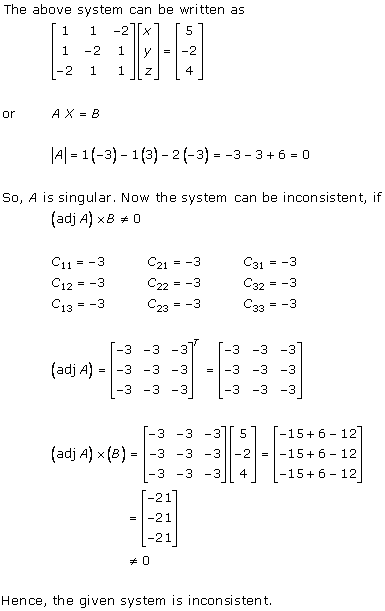
Solution 5

Solution 6
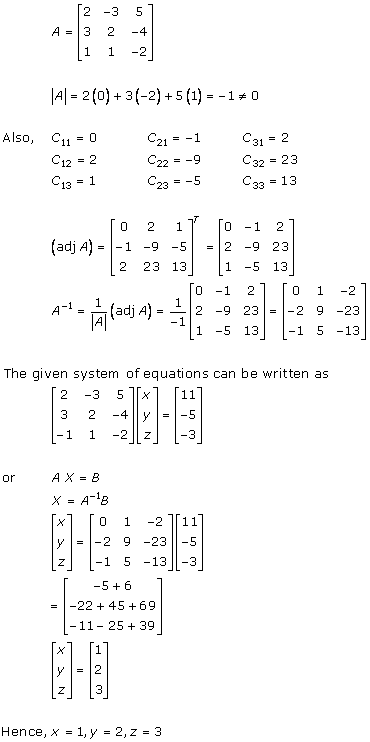
Solution 7
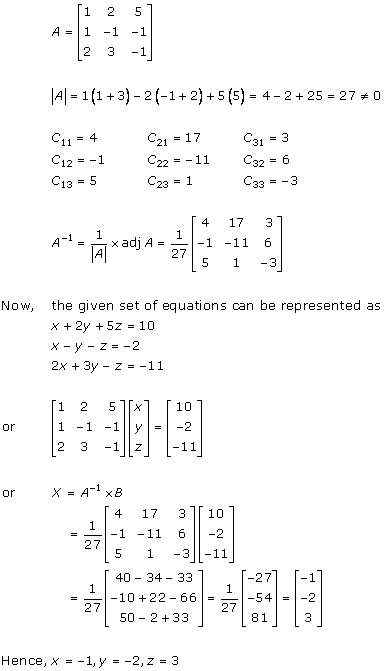
Solution 8(i)
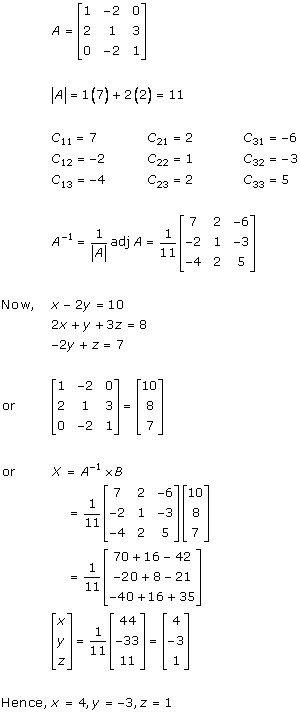
Solution 8(ii)
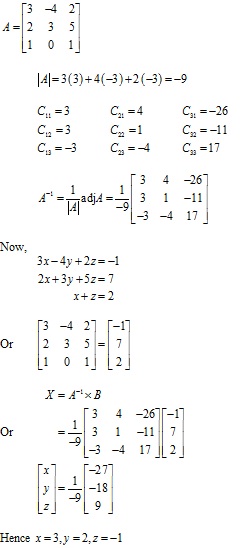
Solution 8(iii)

Solution 8(iv)

Solution 8(v)

Solution 9

Solution 10

Solution 11

Solution 12
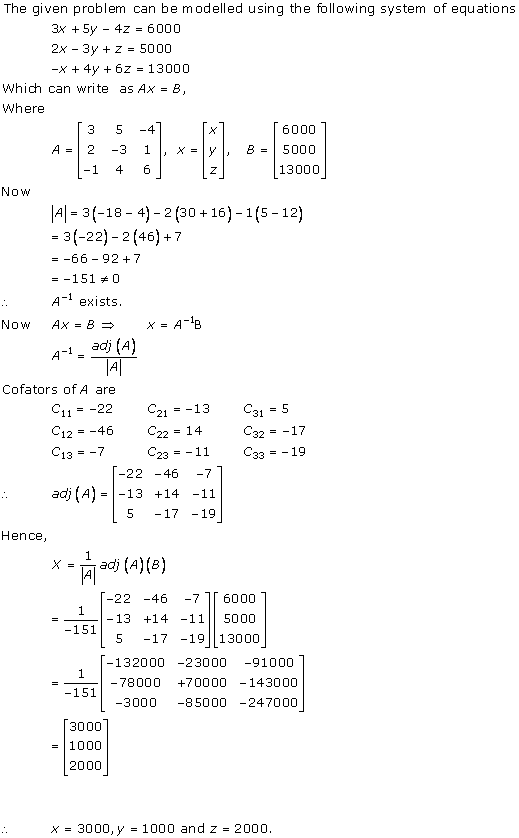
Solution 13


Solution 14
![]()
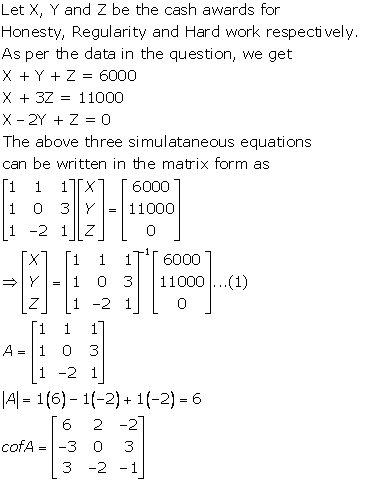

The school can include an award for creativity and extra-curricular activities.
Solution 15


Solution 16
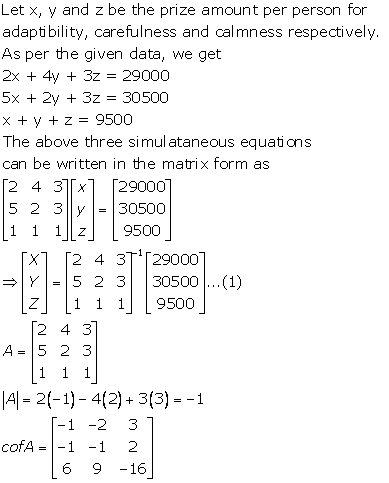

Keeping calm in a tense situation is more rewarding than carefulness, and carefulness is more rewarding than adaptability.
Solution 17
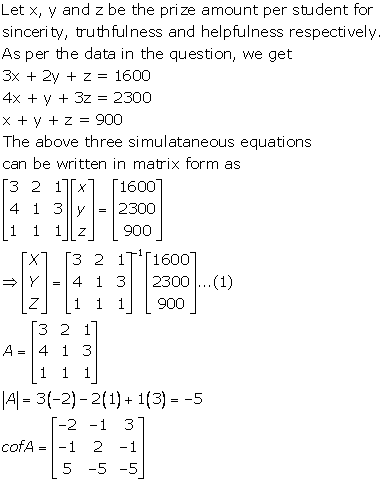
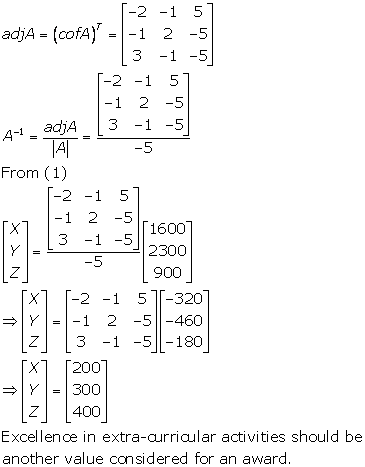
Solution 18

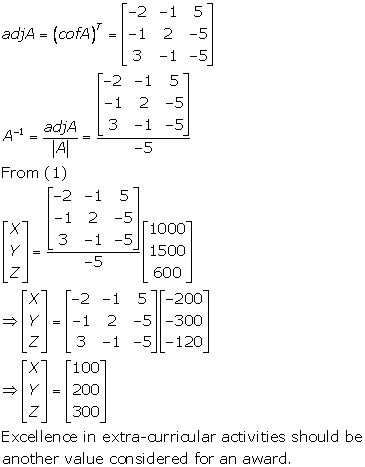
Solution 19

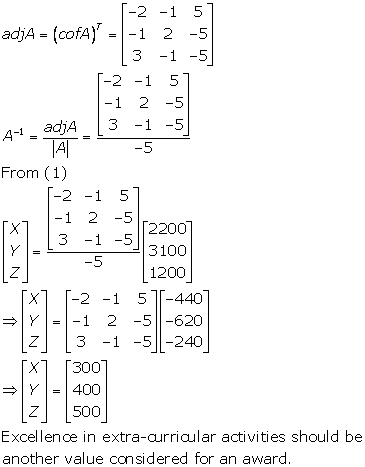
Solution 20
Let the amount deposited be x, y and z respectively.
As per the data in the question, we get


Solution 8(vi)
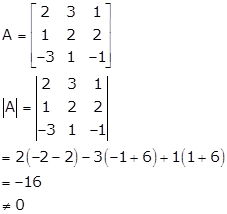
Therefore, A is invertible.
Let Cij be the co-factors of the elements aij.
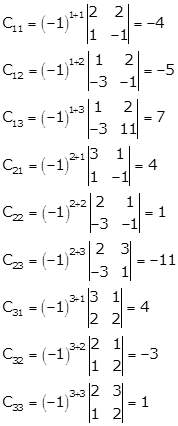
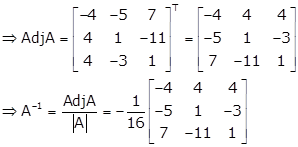
Now, the given system of equations is expressible as
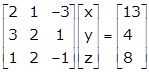
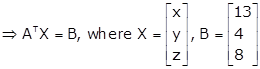
Here we have |AT| = |A| = -16 ≠ 0
Therefore, the given system of equations is consistent with a unique solution given by

Solution 8(vii)
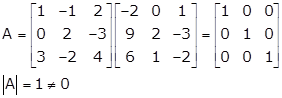
Let 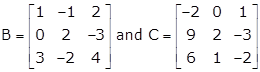
Now, 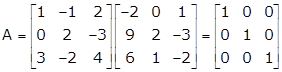

Now, the given system of equations is expressible as

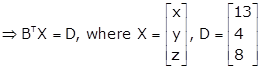
Here we have |BT| = |B| = -1 ≠ 0
Therefore, the given system of equations is consistent with a unique solution given by
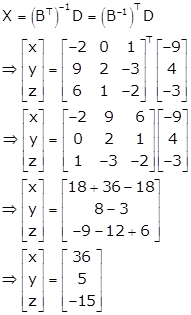
Hence, x = 36, y = 5 and z = -15.
Solution 21
From the given information, we can form a matrix as follows

Applying R2→ R2 - 4R1, R3→ R3 - 6R1
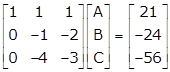
Applying R3→ R3 + (-4R1)
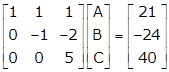
From the above matrix form, we get
A + B + C = 21 … (i)
-B - 2C = -24 … (ii)
5C = 40
⇒ C = 8 … (iii)
Putting the value of C in (ii), we get
B = 8
Substituting B and C in (i), we get
C = 5
Hence, cost of variety 'A' pen is Rs. 8, cost of variety B pen is Rs. 8 and cost of variety 'C' pen is Rs. 5.
Solution of Simultaneous Linear Equations Exercise Ex. 8.2
Solution 1

Solution 2

Solution 3

Solution 4

Solution 5

Solution 6

Solution 7
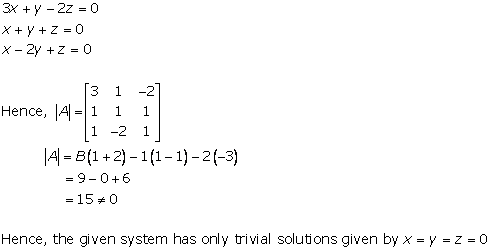
Solution 8

Solution of Simultaneous Linear Equations Exercise MCQ
Solution 1

Solution 2

Solution 3

Solution 4

Solution 5

Solution 6

Solution 7

Solution 8
Correct optio : (a)
x + 2y + 3z = 1
2x + y + 3z = 2
5x + 5y + 9z = 4
The determinant of the coefficient matrix  is
is
= -6-2 (18 - 15) + 3(10 - 5)
= -6 - 6 + 15
= 3 ≠ 0
The right hand side is also non zero.
The system has a unique solution.
Solution 9

Solution 10

Solution of Simultaneous Linear Equations Exercise Ex. 8VSAQ
Solution 1
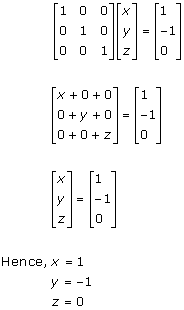
Solution 2
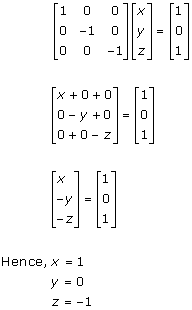
Solution 3
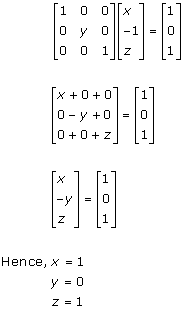
Solution 4

Solution 5
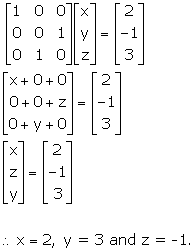
Solution 6