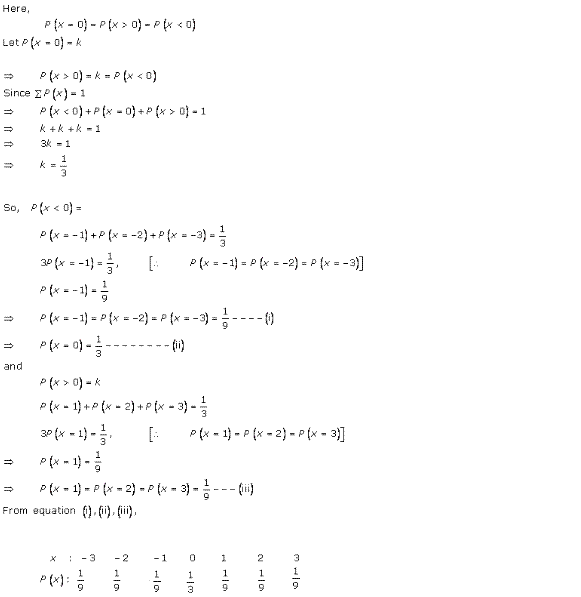Class 12-science RD SHARMA Solutions Maths Chapter 32 - Mean and variance of a random variable
Ex. 32.1
Ex. 32.2
MCQ
Ex. 32VSAQ
Mean and variance of a random variable Exercise Ex. 32.1
Solution 1
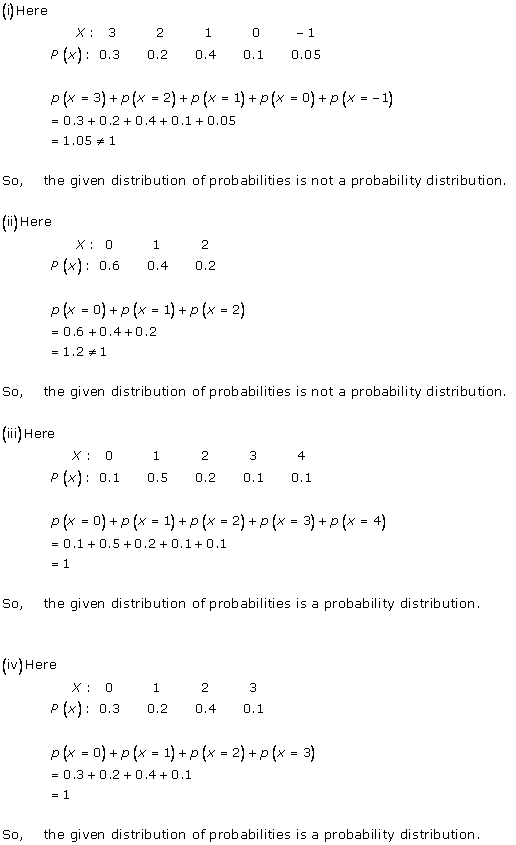
Solution 2

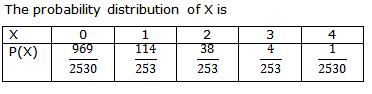
Solution 3
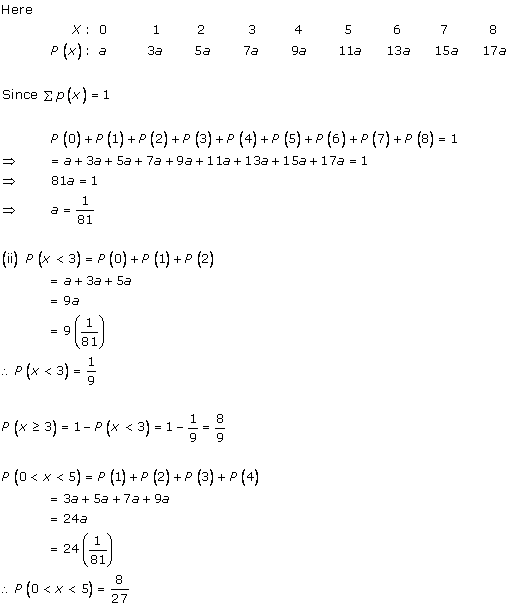
Solution 4


Solution 5

Solution 6
Solution 7

Solution 8
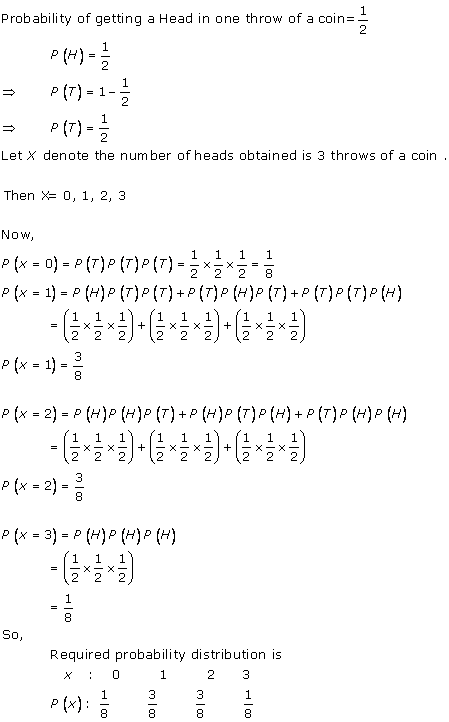
Solution 9

Solution 10

Solution 11

Solution 12
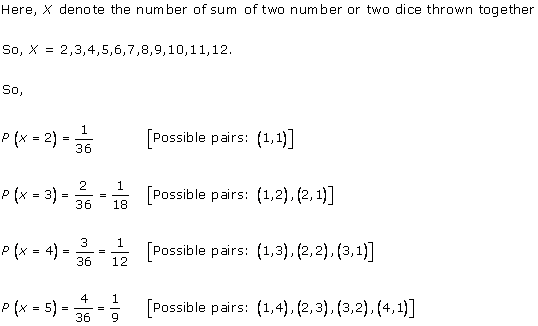

Solution 13

Solution 14


Solution 15
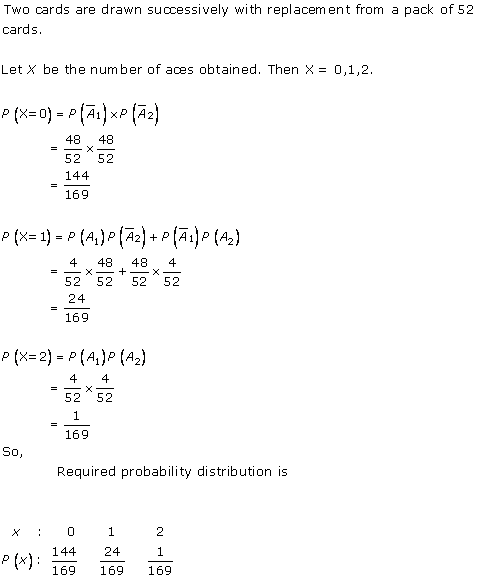
Solution 16
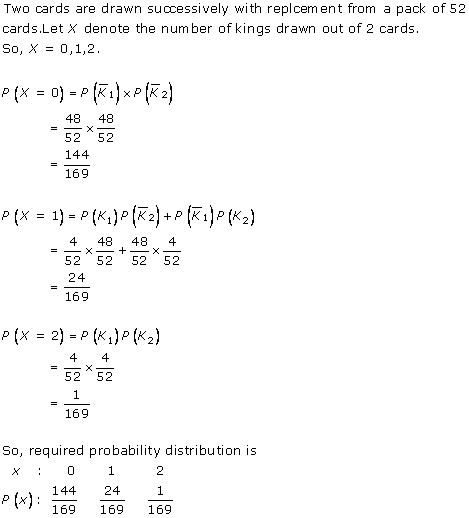
Solution 17

Solution 18

Solution 19
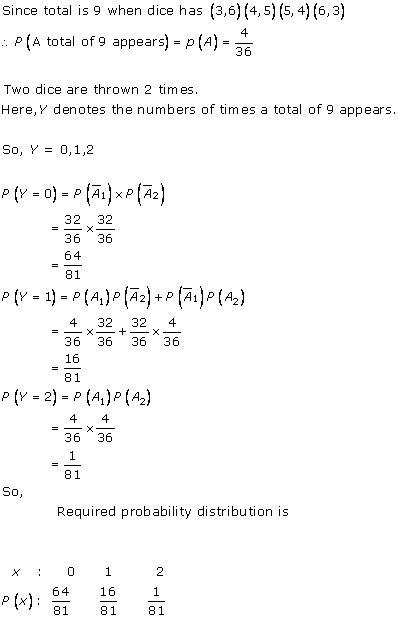
Solution 20
Solution 21

Solution 22

Solution 23

Solution 24
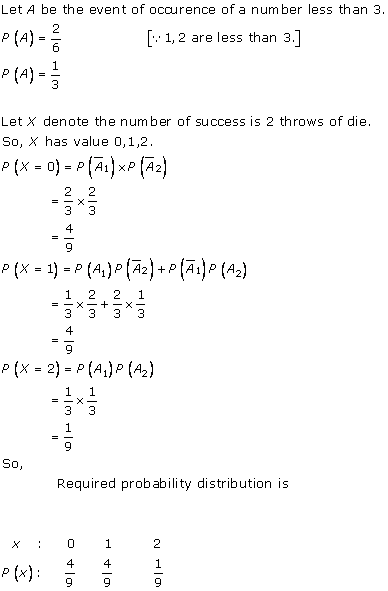
Solution 25
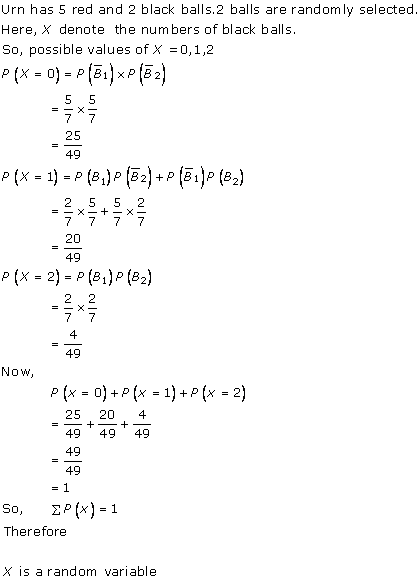
Solution 26

Solution 27

Solution 28

Solution 29
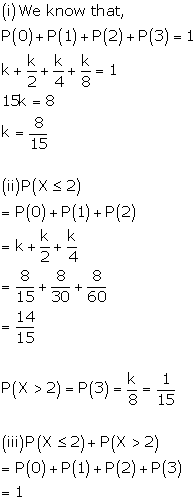
Mean and variance of a random variable Exercise Ex. 32.2
Solution 1(i)

Solution 1(ii)
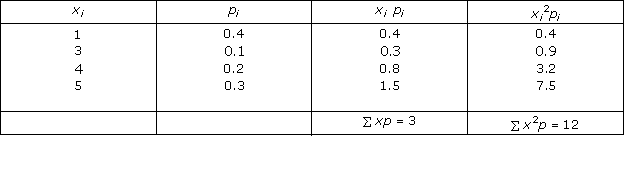
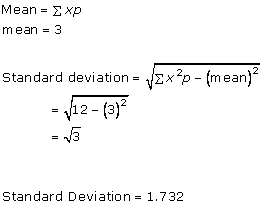
Solution 1(iii)
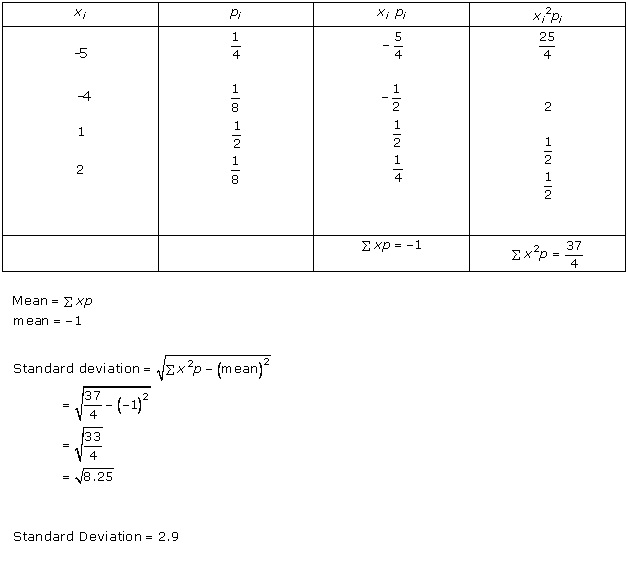
Solution 1(iv)
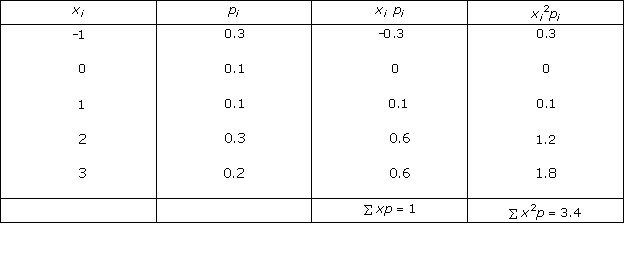
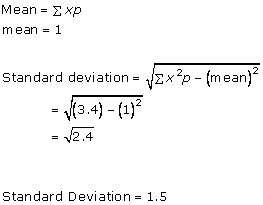
Solution 1(v)
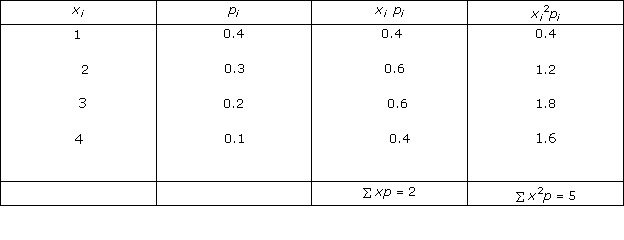
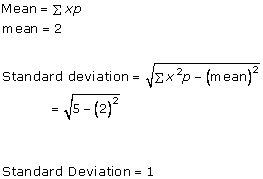
Solution 1(vi)
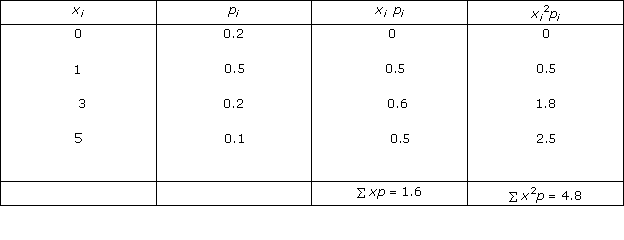

Solution 1(vii)
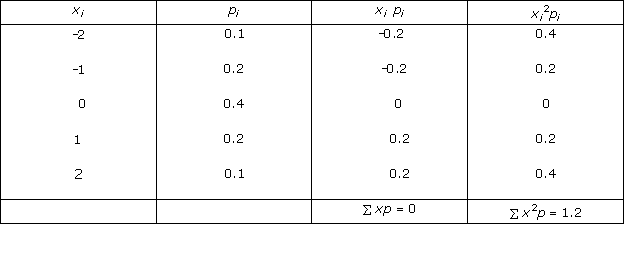
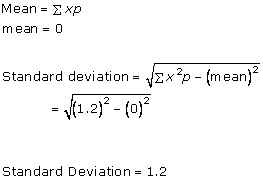
Solution 1(viii)
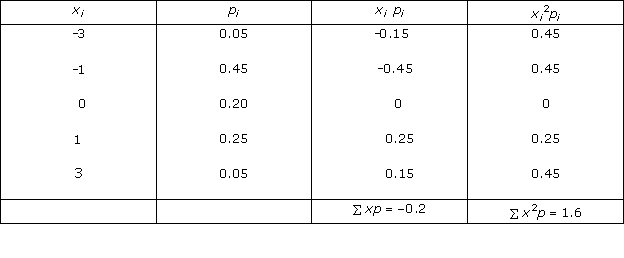

Solution 1(ix)

Solution 2
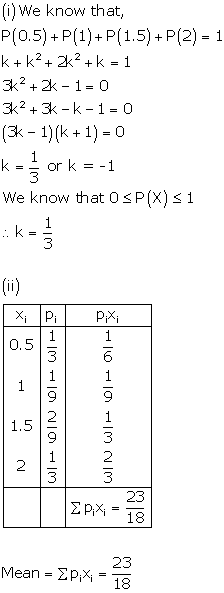
Solution 3


Solution 4
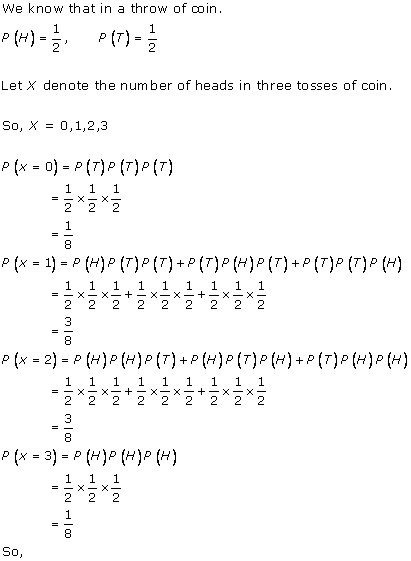
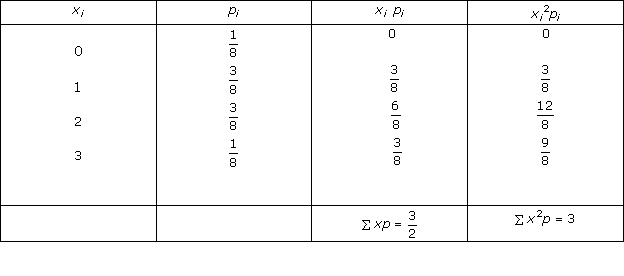
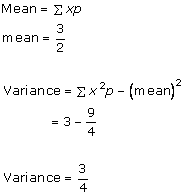
Solution 5

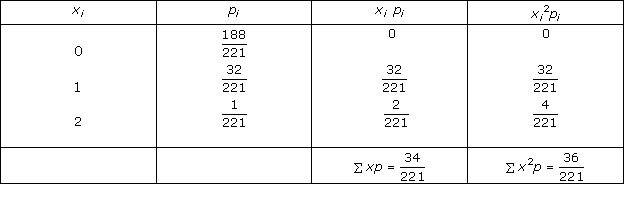

Solution 6


Solution 7
Solution 8
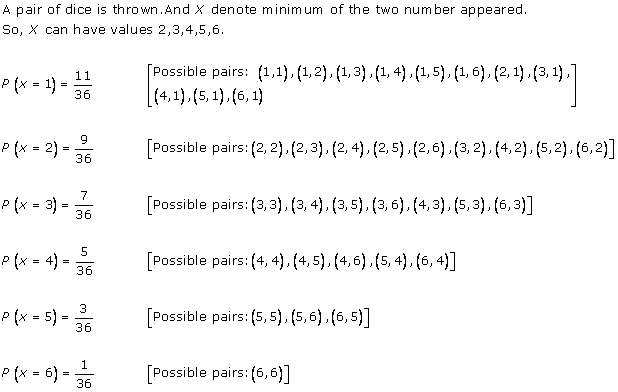
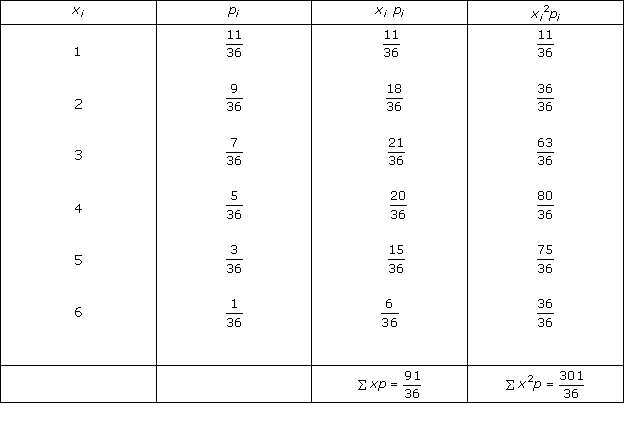

Solution 9
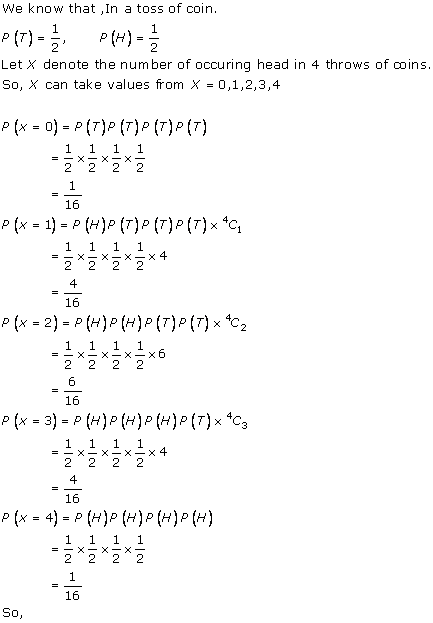
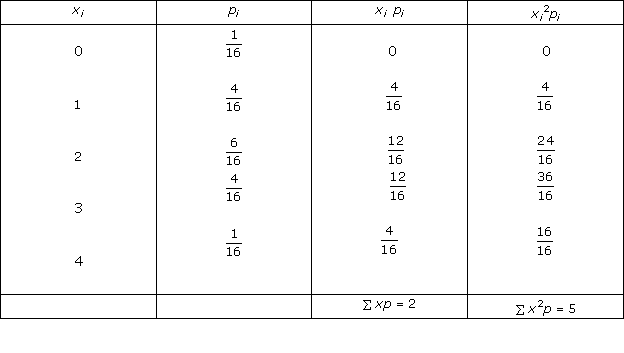

Solution 10

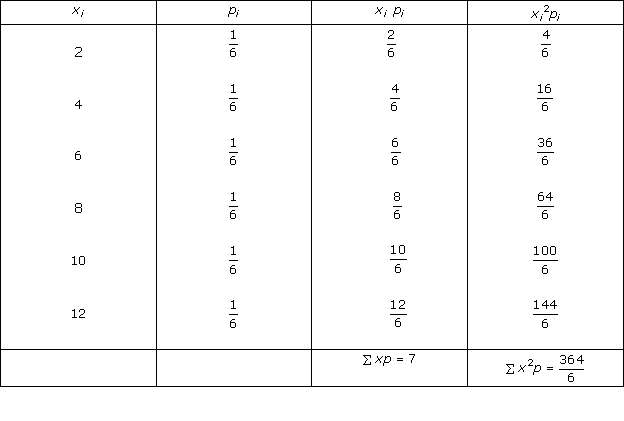
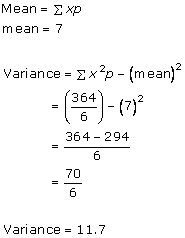
Solution 11

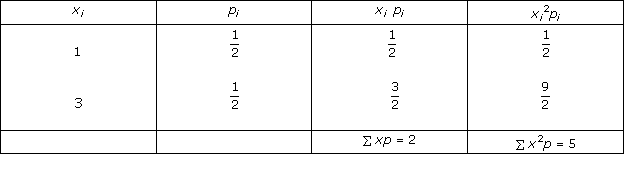
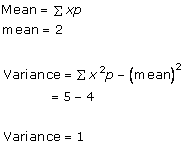
Solution 12
Solution 13
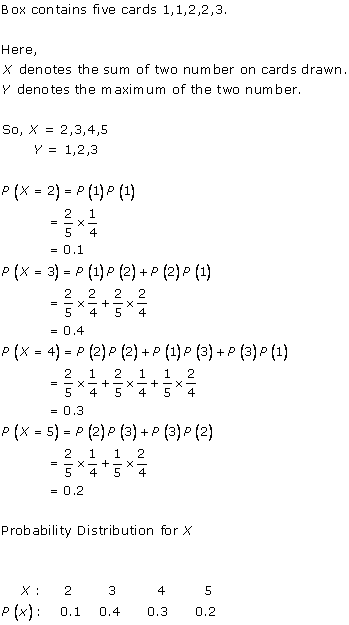
![]()
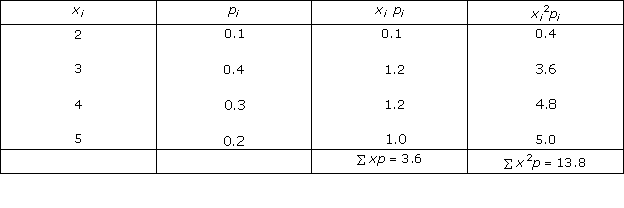

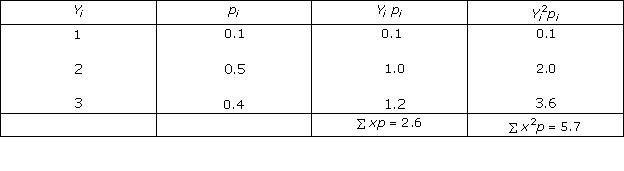

Solution 14

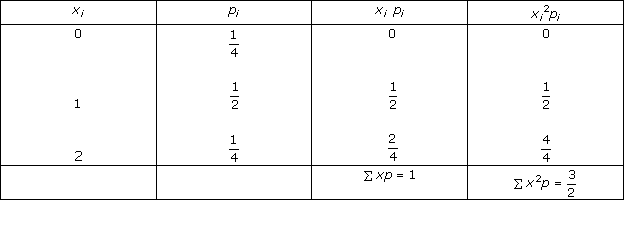

Solution 15

Solution 16

Solution 17

Solution 18

Solution 19

Mean and variance of a random variable Exercise MCQ
Solution 1
Correct option: (d)

Solution 2
Correct option: (b)

Solution 3
Correct option: (d)

Solution 4
Correct option: (a)
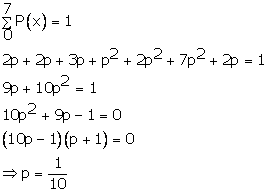
Solution 5
Correct option: (d)

Solution 6
Correct option: (c)
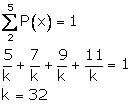
NOTE: Question is modified.
Solution 7
Correct option: (d)

Solution 8
Correct option: (d)

Solution 9
Correct option: (c)
Variance of discrete random variable is always E(X2) - (E(X))2
Mean and variance of a random variable Exercise Ex. 32VSAQ
Solution 1

Solution 2

Solution 3
![]()
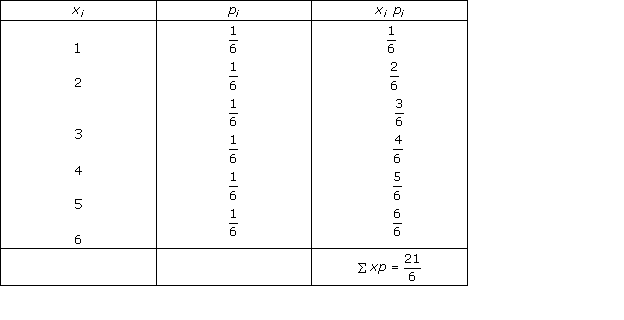
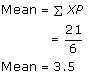
Solution 4
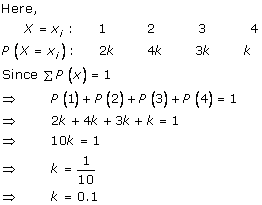
Solution 5

Solution 6
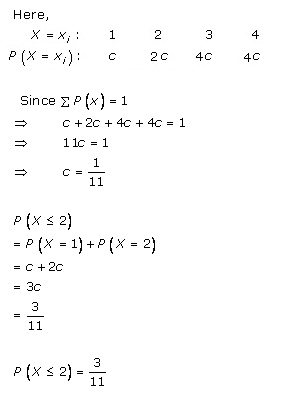
![]()
Solution 7