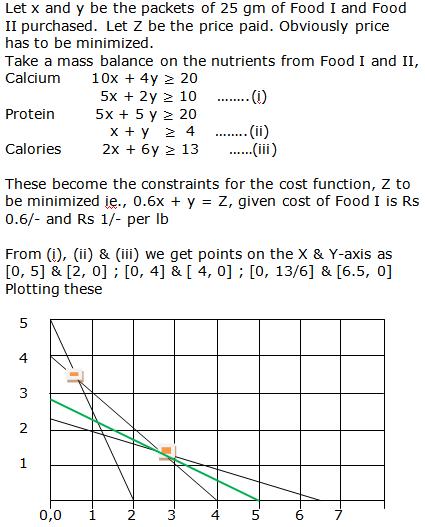
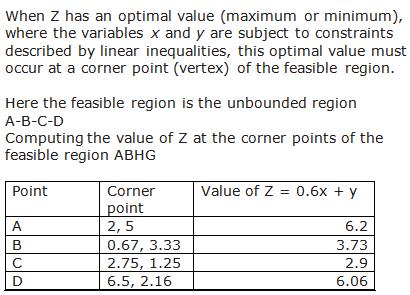
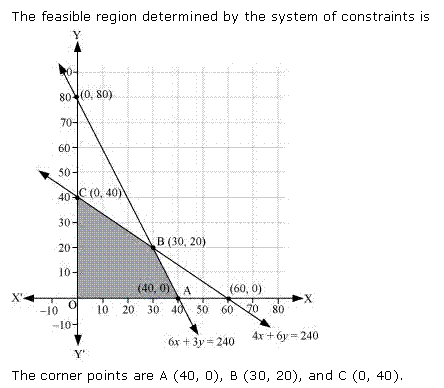
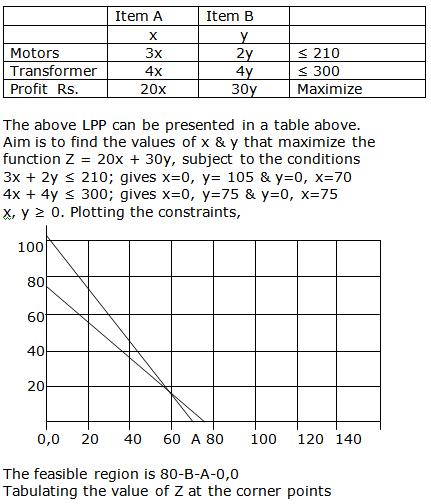
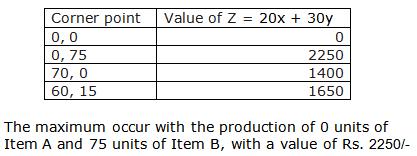
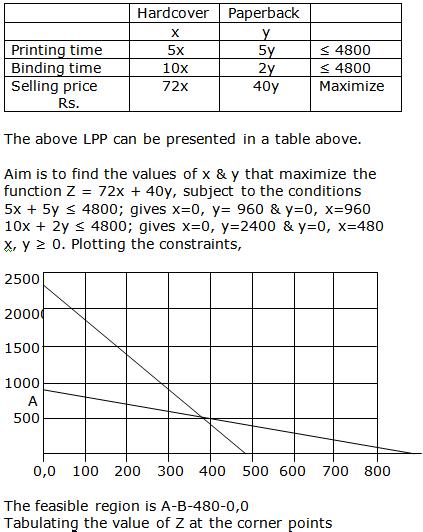
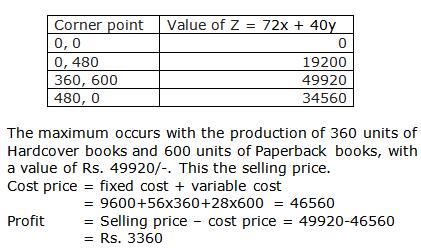
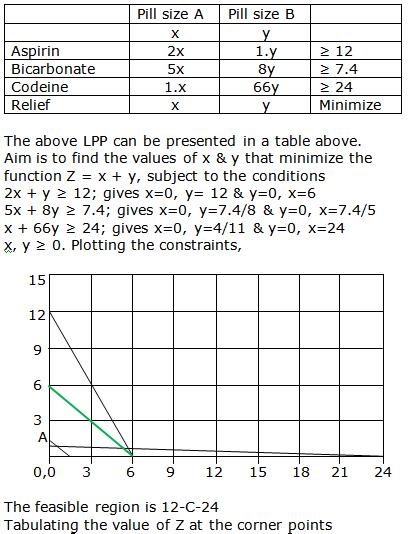
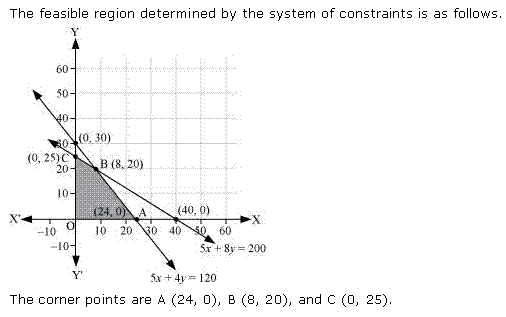
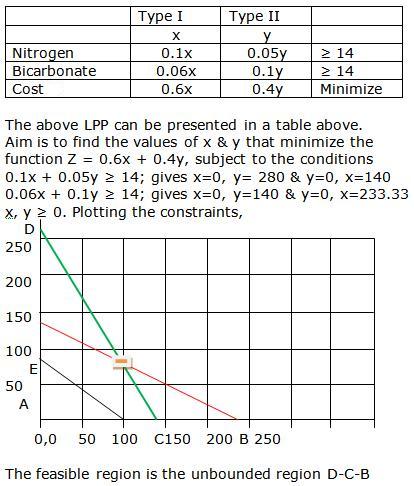
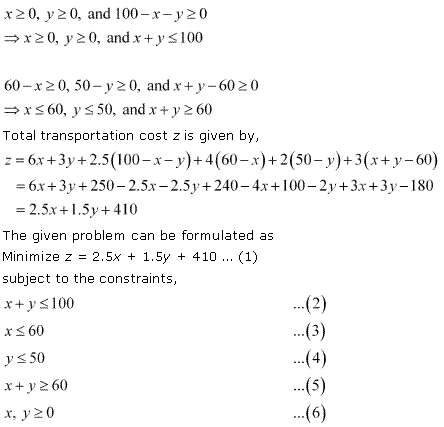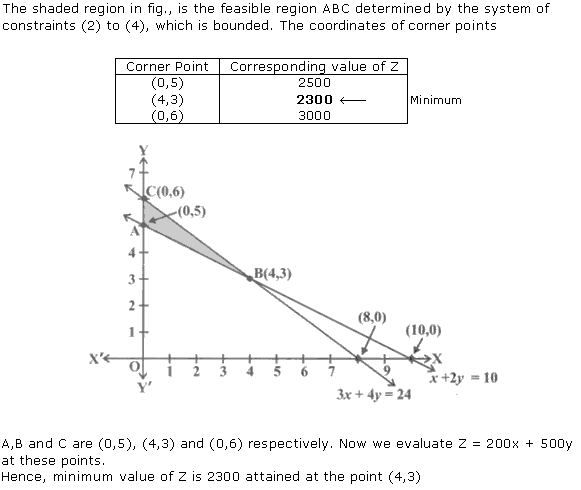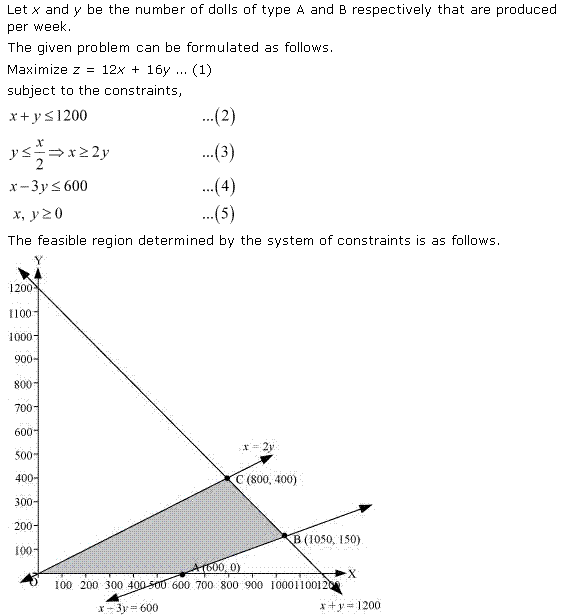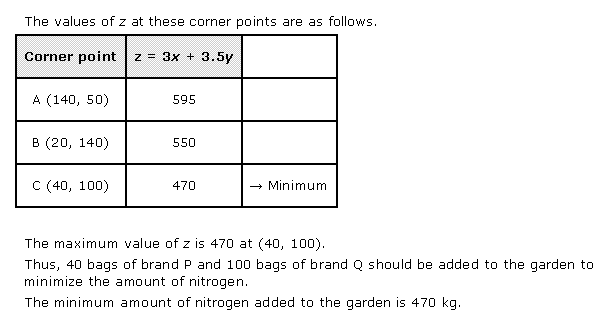Class 12-science RD SHARMA Solutions Maths Chapter 30 - Linear programming
Linear programming Exercise Ex. 30.1
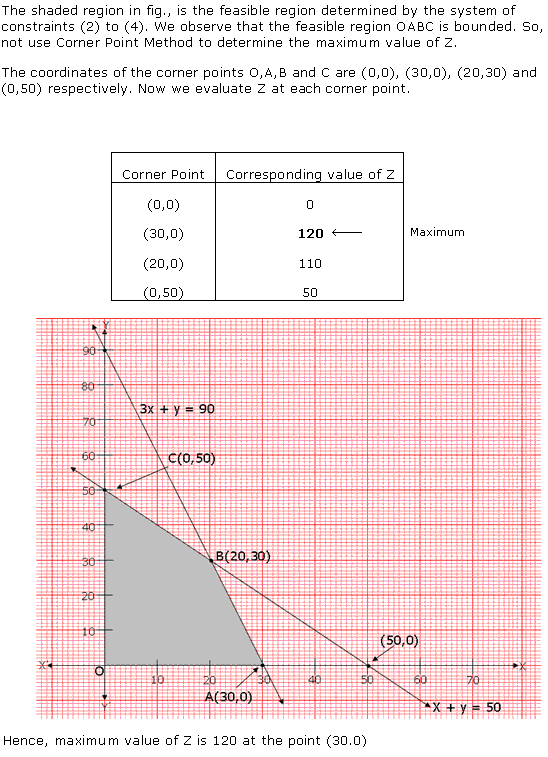
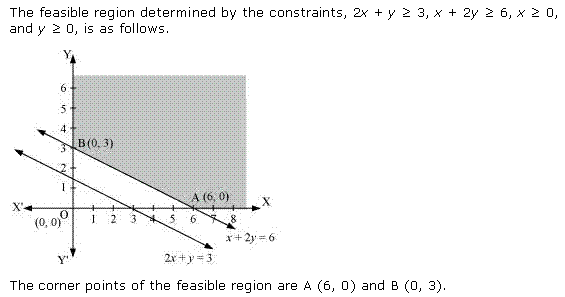
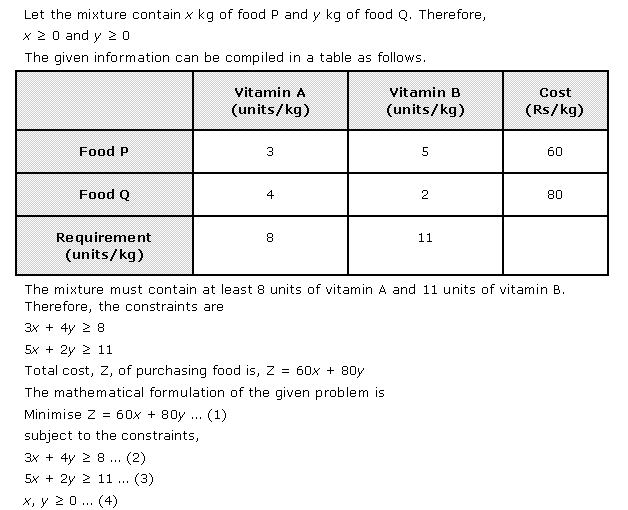
Solution 1
![]()


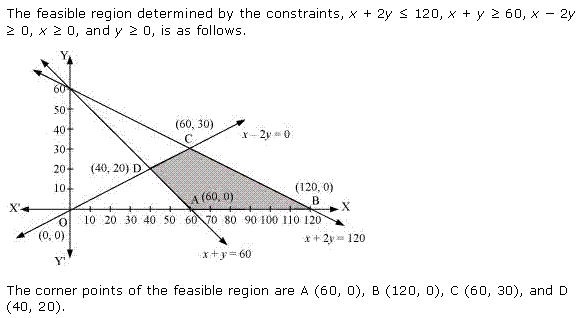
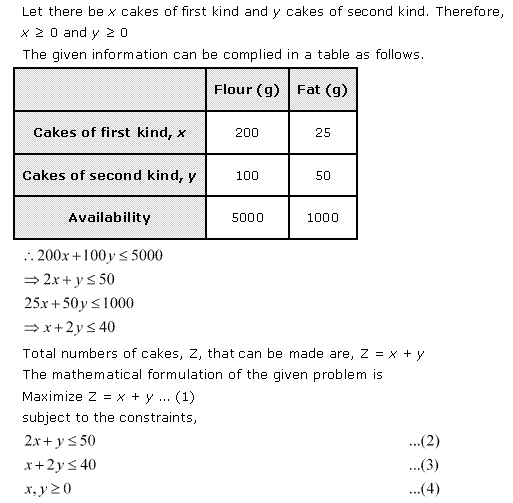
Solution 2
![]()

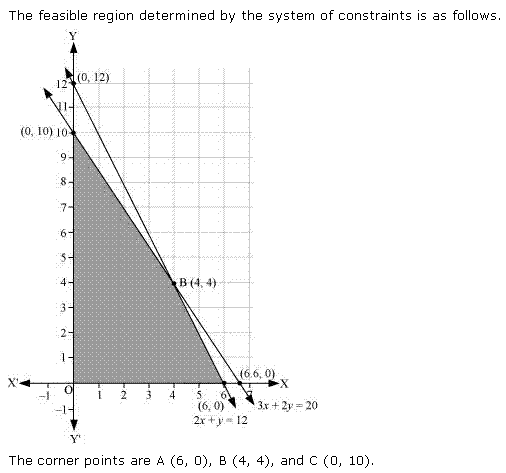
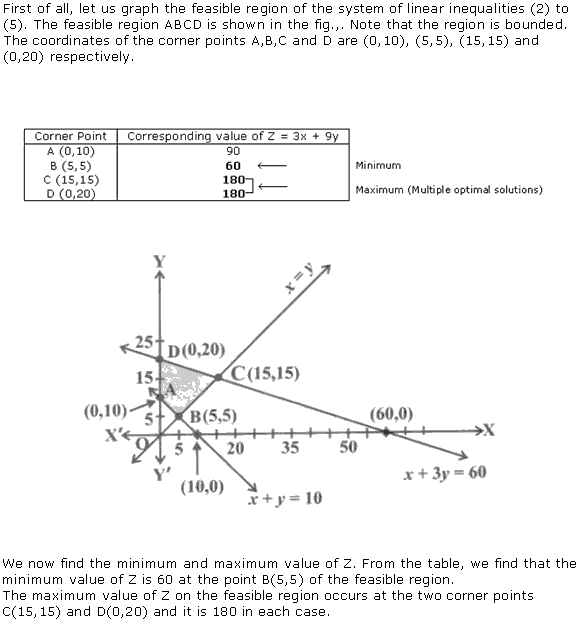
Solution 3


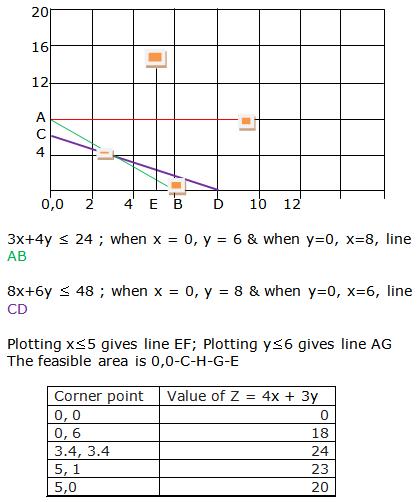
Solution 4
![]()


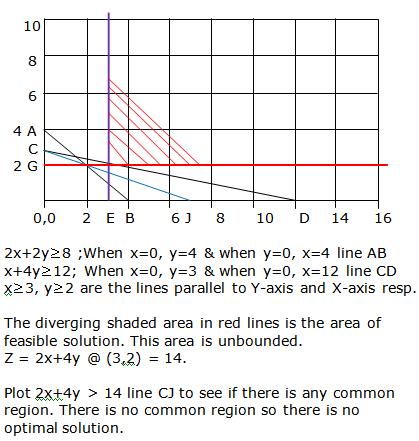
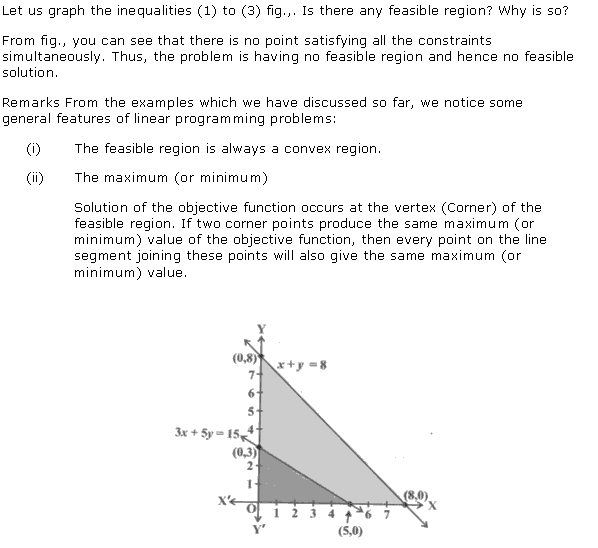
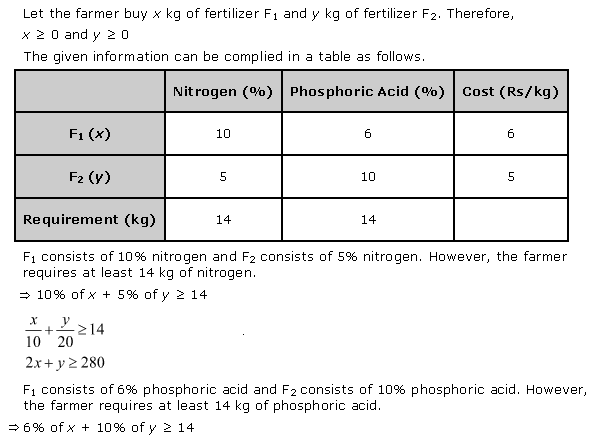
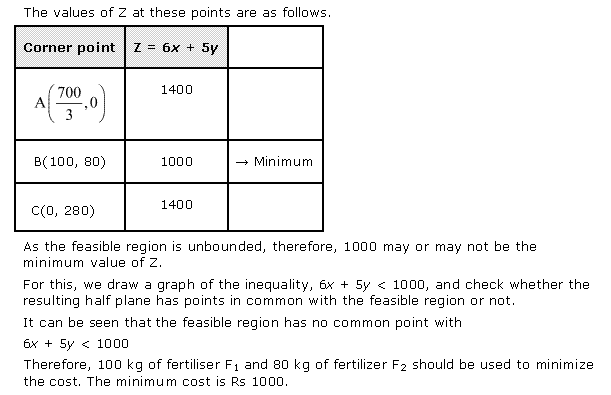
Solution 5
![]()

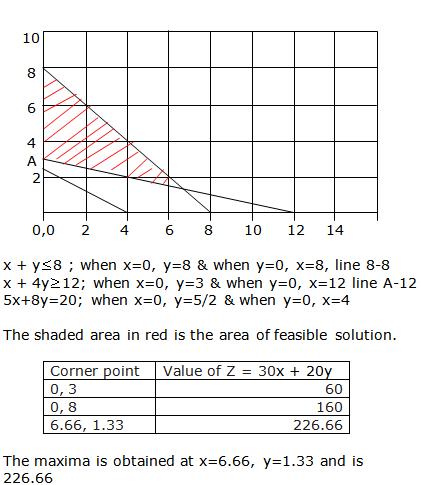
Solution 6
![]()


Solution 7
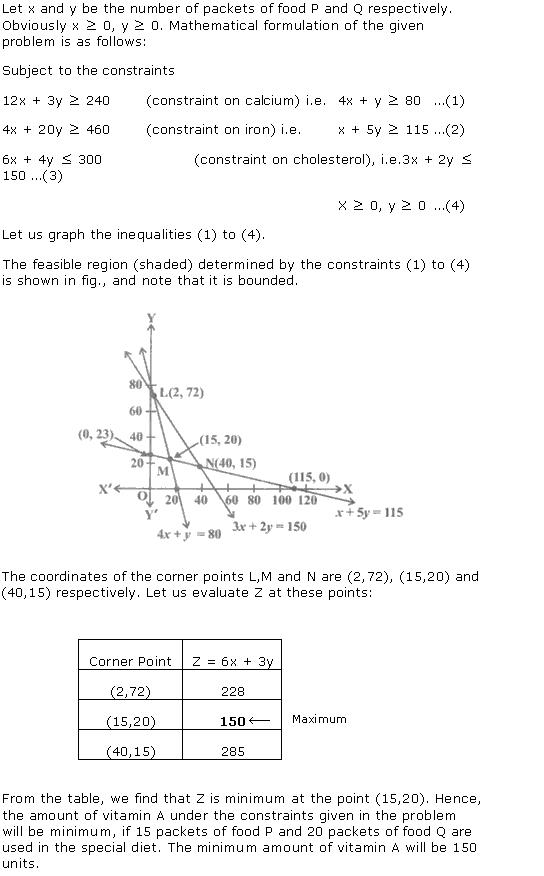
Solution 8


Solution 9
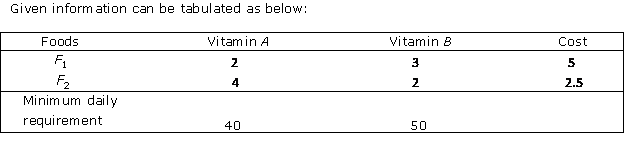
Solution 10
Solution 11
Solution 12
Solution 13


Solution 14

Solution 15


Linear programming Exercise Ex. 30.2
Solution 1

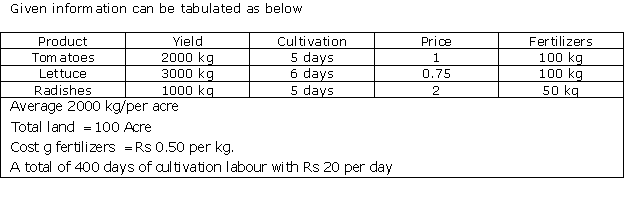
Solution 2
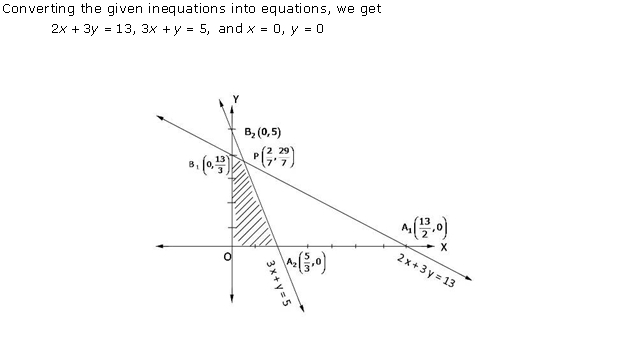

Solution 3


Solution 4
Solution 5
Solution 6
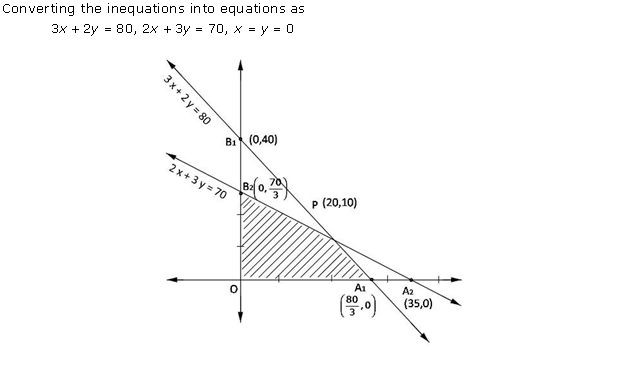

Solution 7
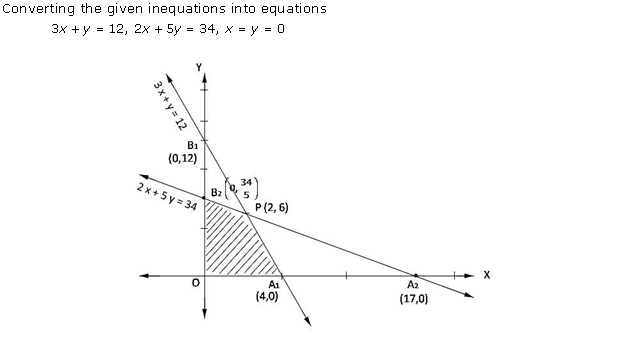
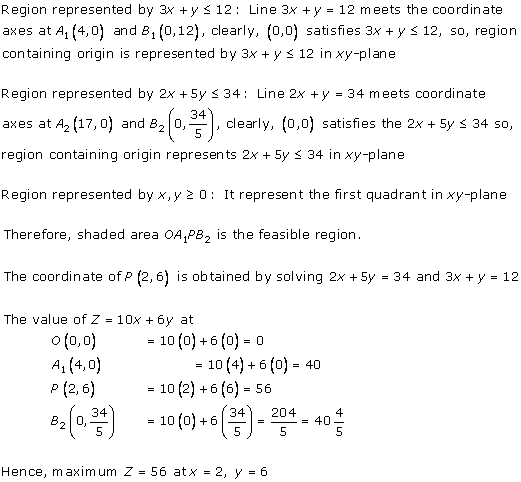
Solution 8
Solution 9
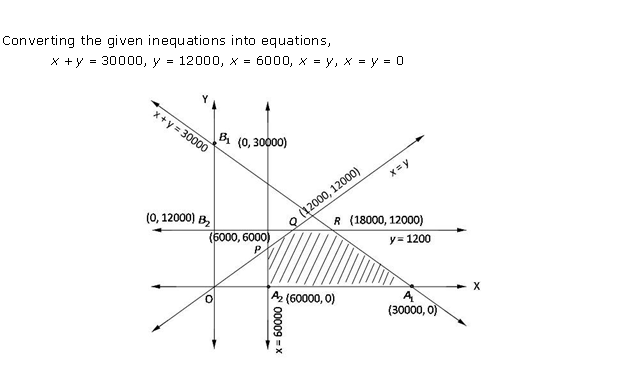

Solution 10
Solution 11
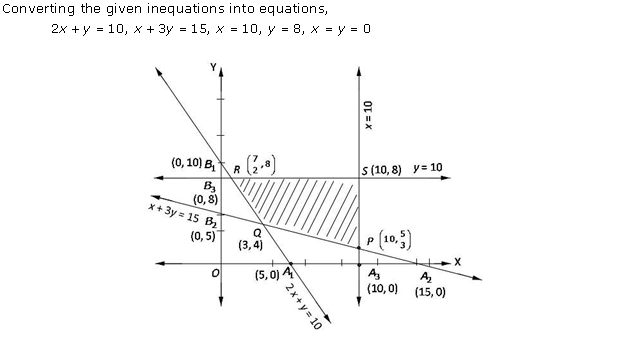
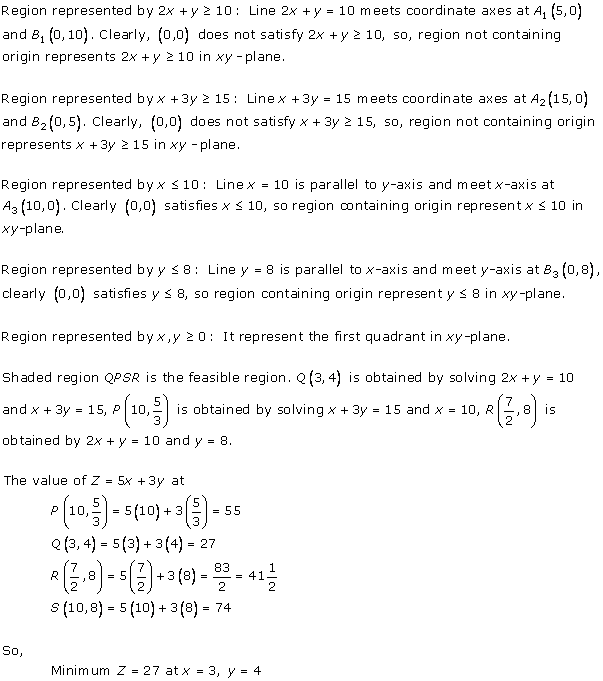
Solution 12
Solution 13 Old
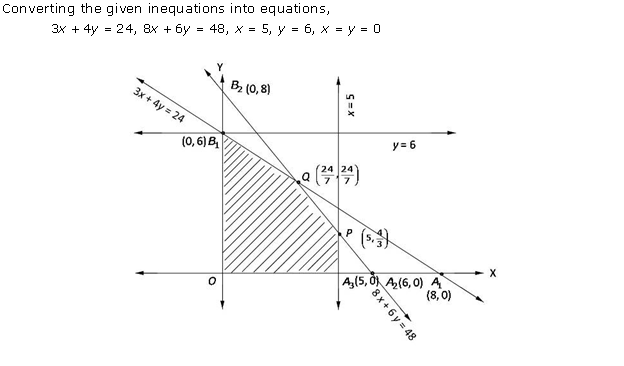

Solution 14
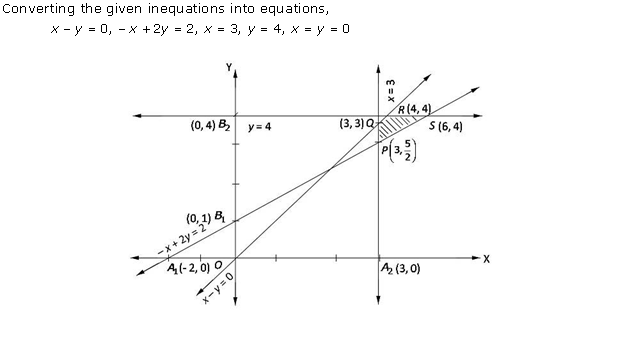

Solution 15


Solution 16
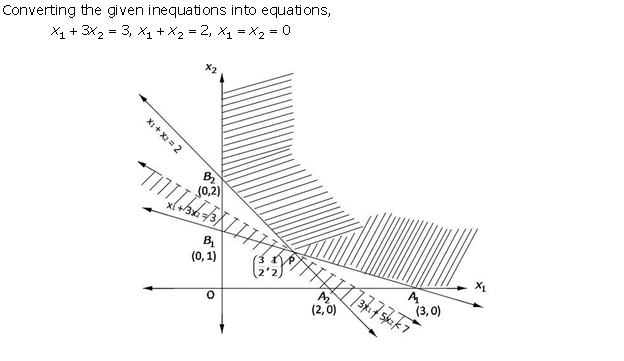

Solution 17
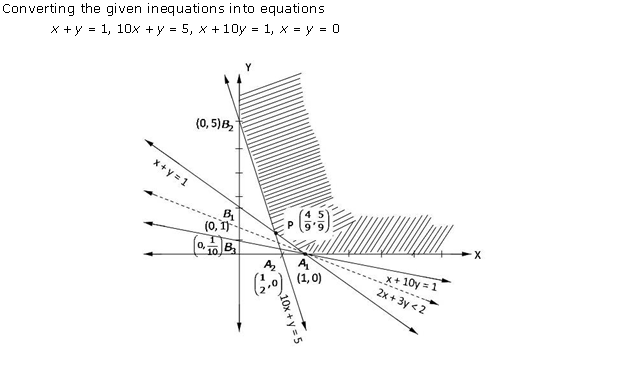

Solution 18


Solution 19
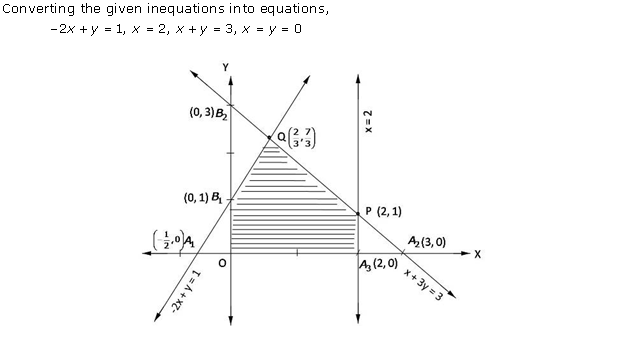

Solution 20
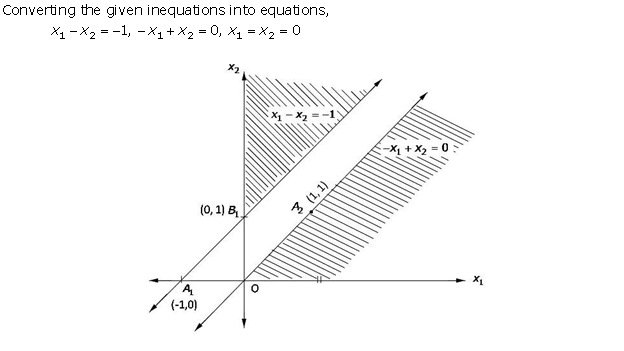

Solution 21
Solution 22

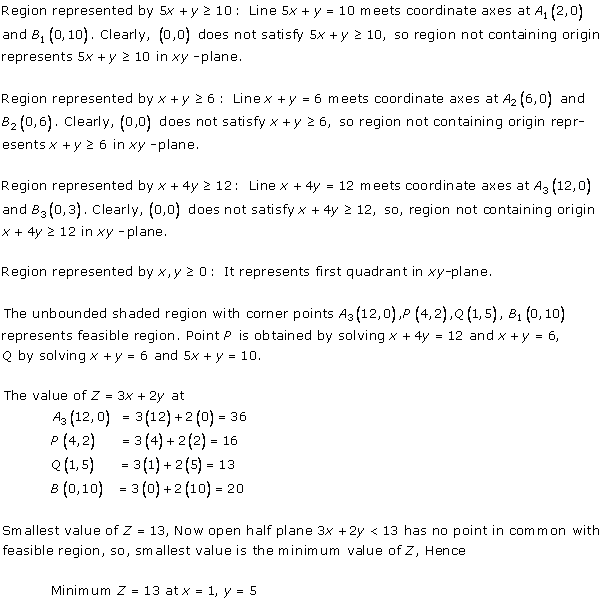
Solution 23
Solution 24
Solution 25
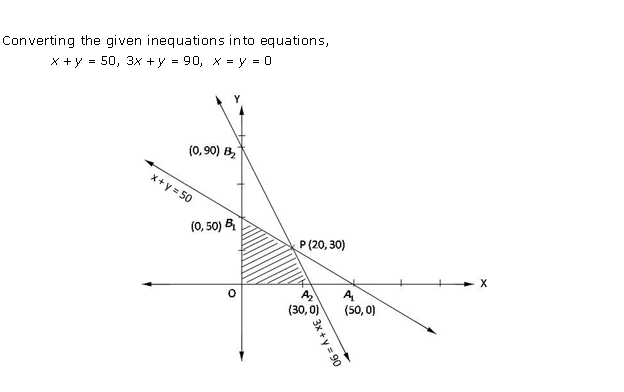

Solution 26
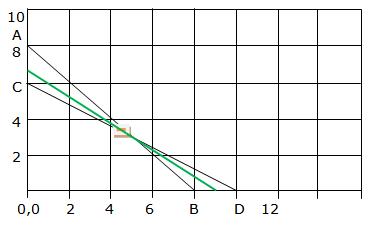
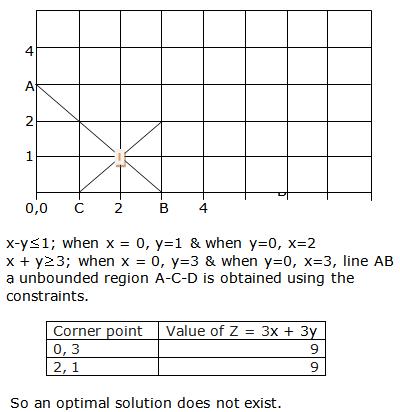
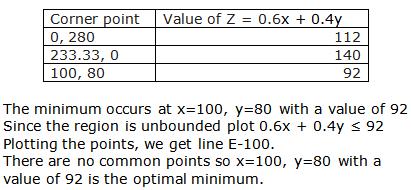
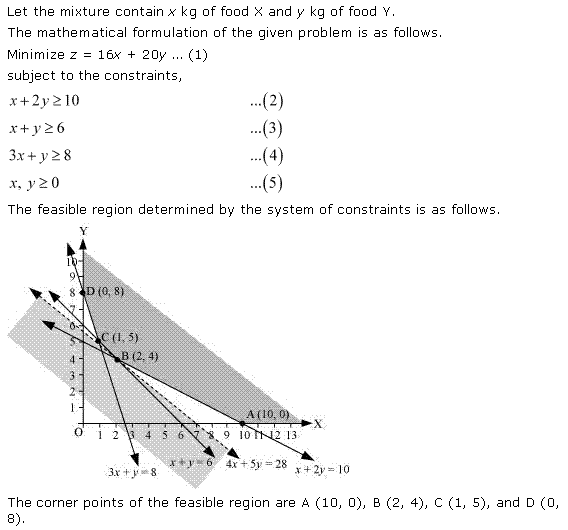
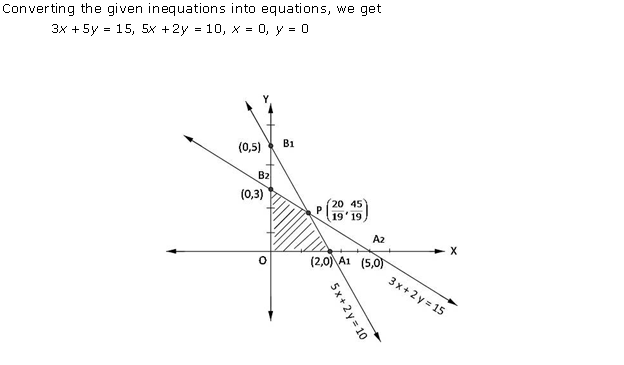
Converting the inequations into equations, we obtain the lines
2x + 4y = 8, 3x + y = 6, x + y = 4, x = 0, y = 0.
These lines are drawn on a suitable scale and the feasible region of the LPP is shaded in the graph.
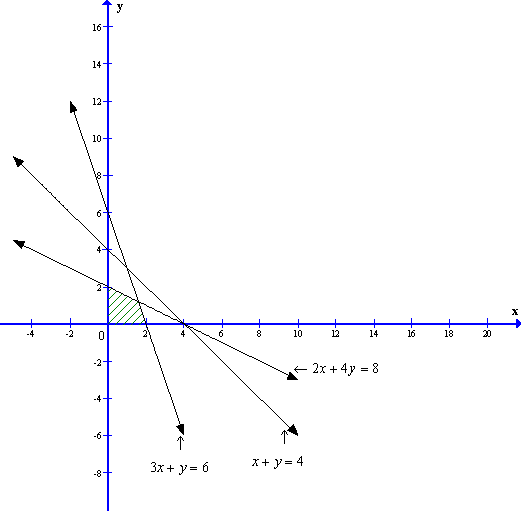
From the graph we can see the corner points as (0, 2) and (2, 0).
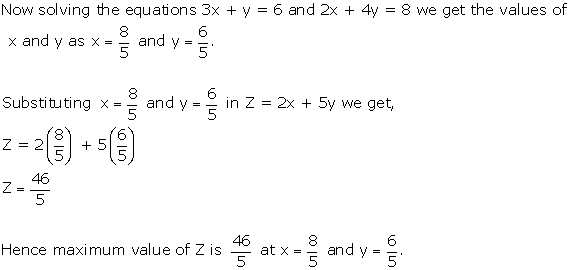
Linear programming Exercise Ex. 30.3
Solution 1
Solution 2

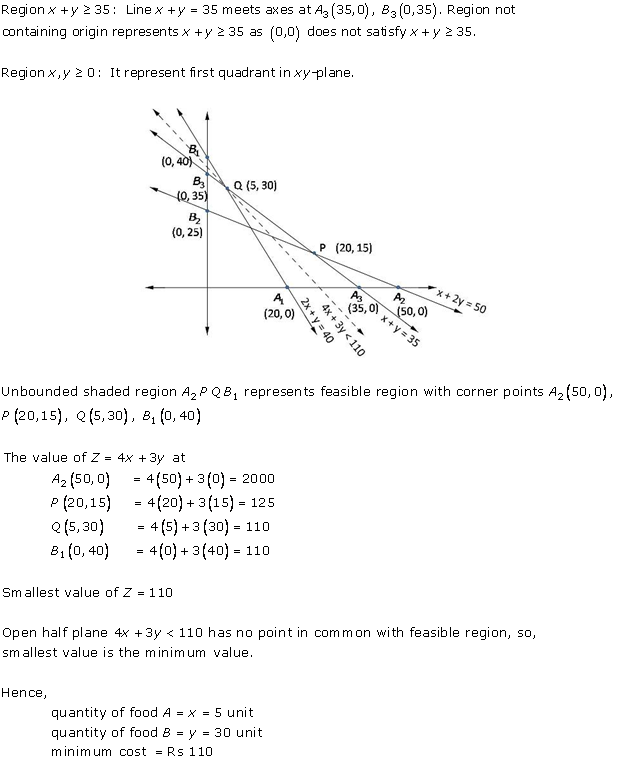
Solution 3
Solution 4

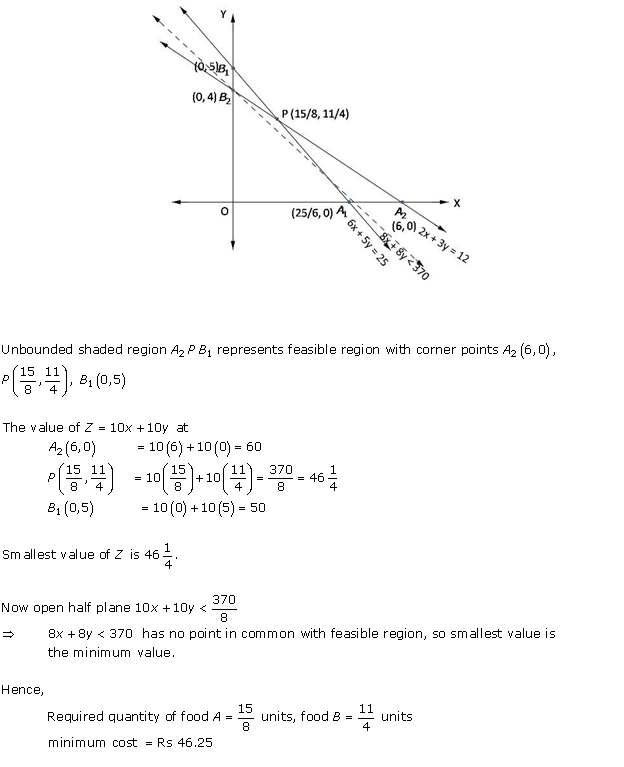
![]()
Solution 5

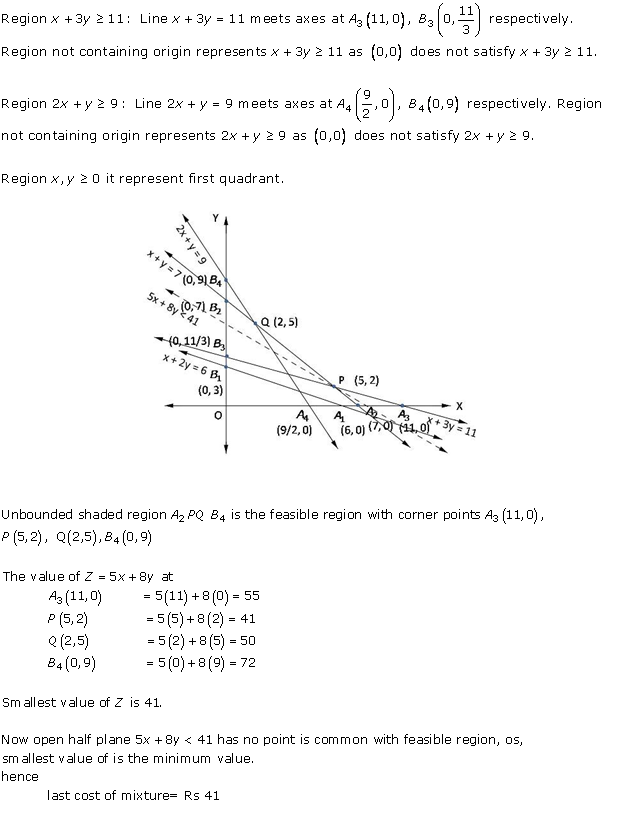
Solution 6


Solution 7


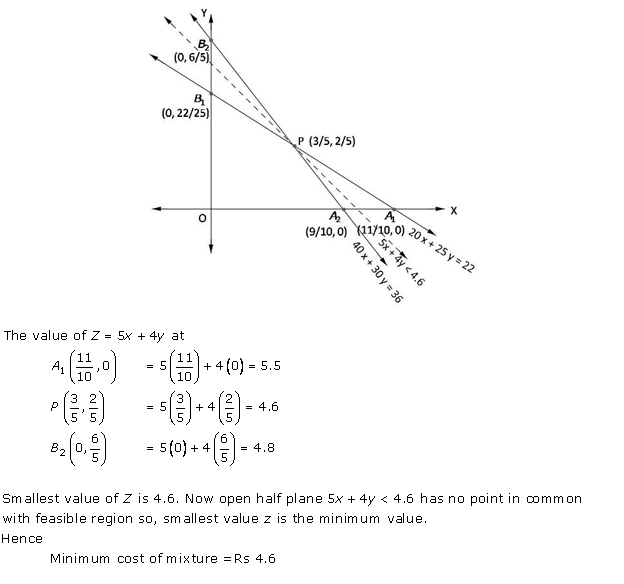
Solution 9

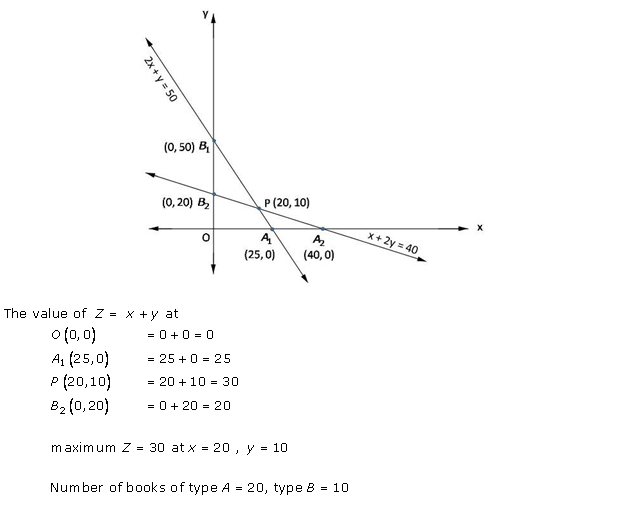
Solution 8

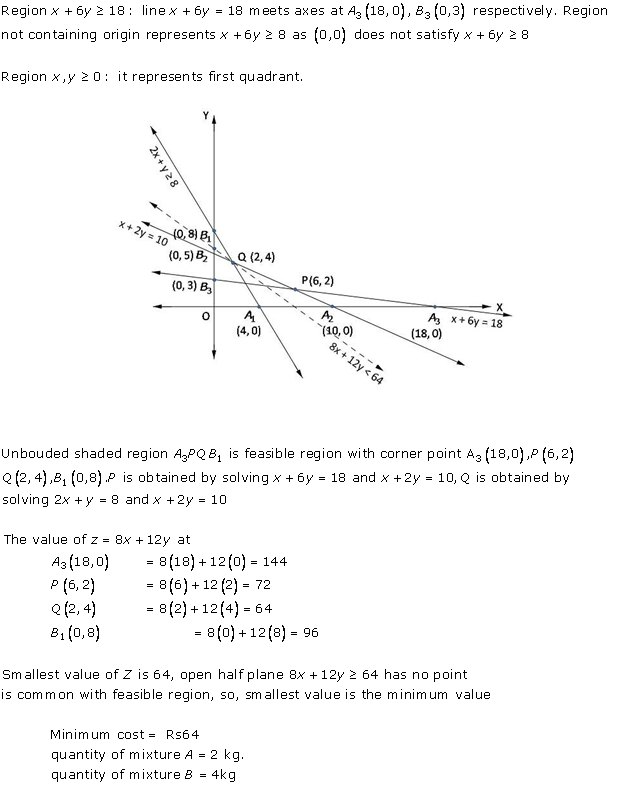
Solution 10

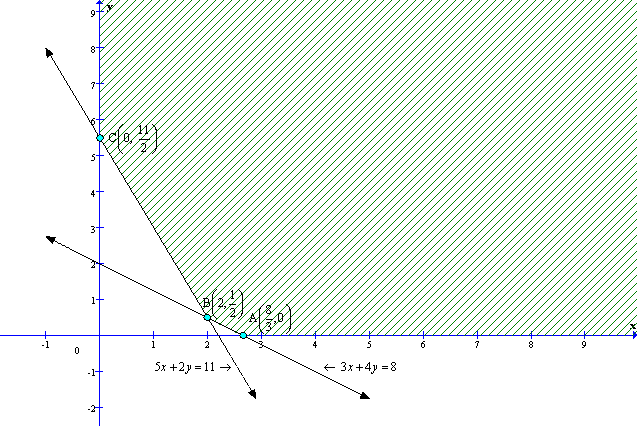

Solution 11

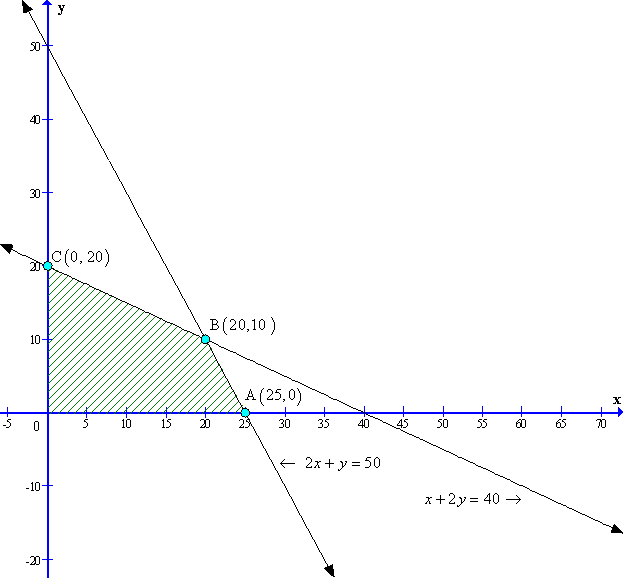

Solution 12

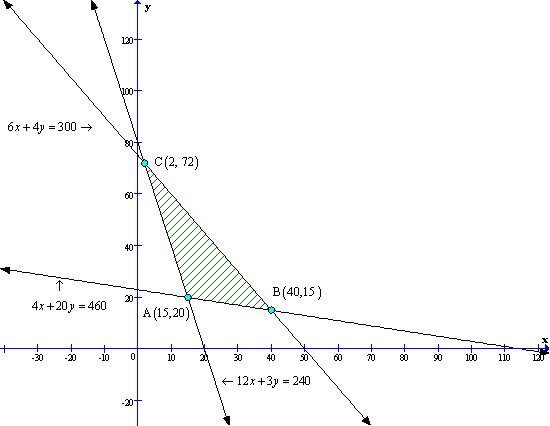

Solution 13

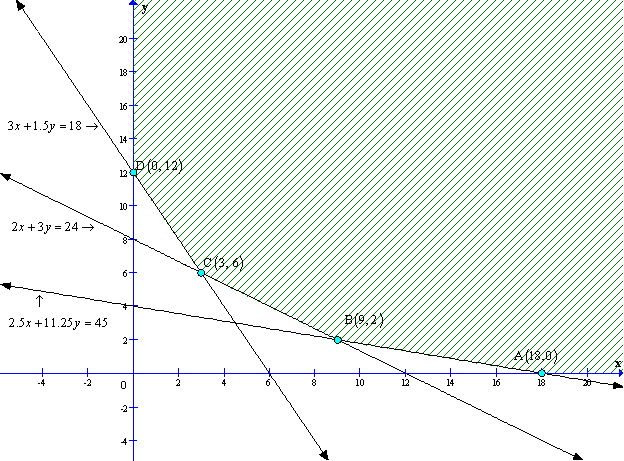

Note: Answer given in the book is incorrect.
Solution 14



Solution 15

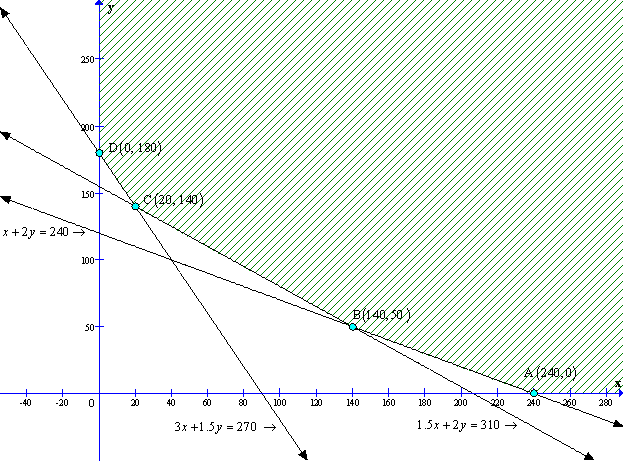

Linear programming Exercise Ex. 30.4
Solution 1

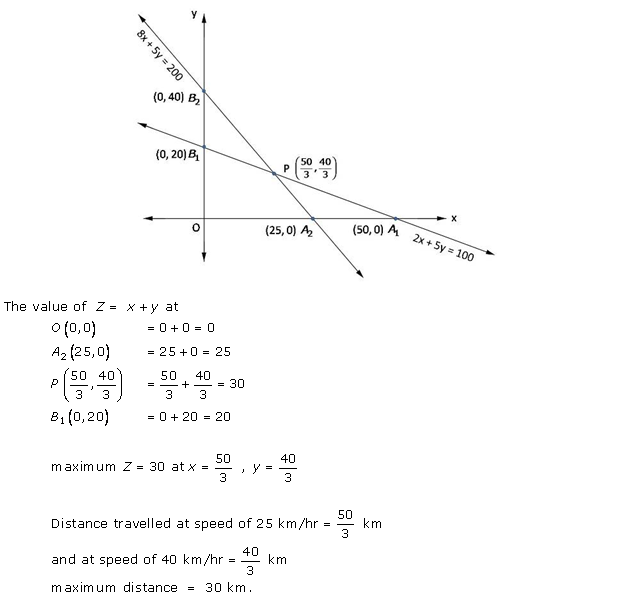
Solution 2

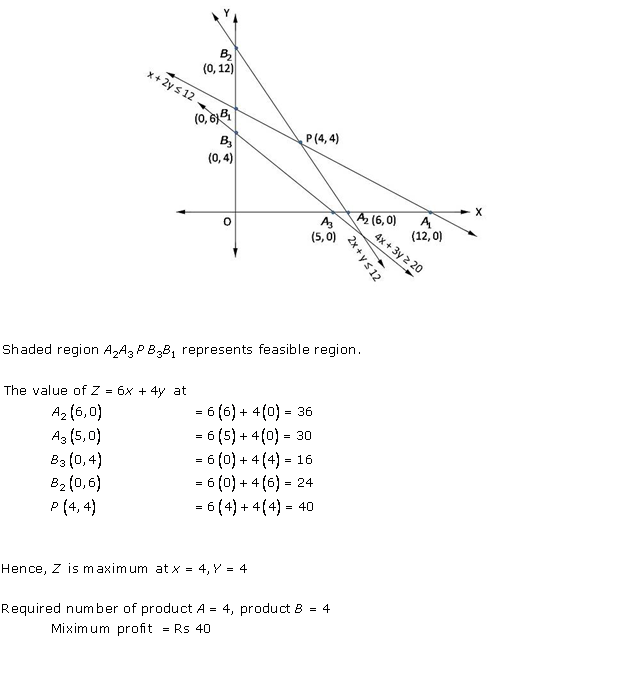
Solution 3

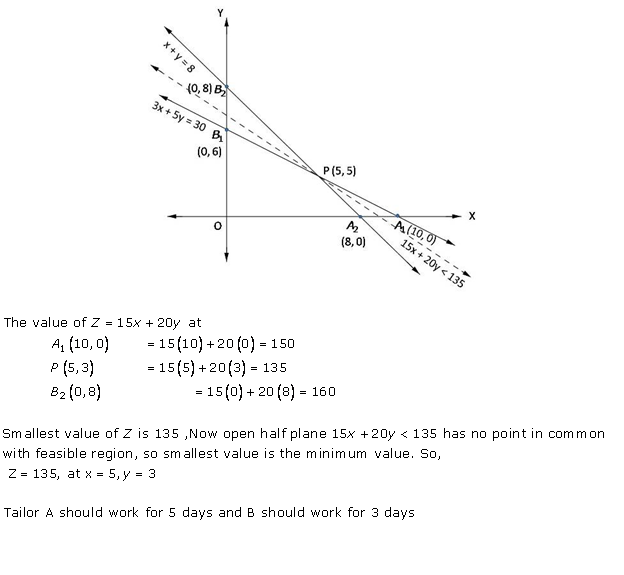
Solution 4
Solution 5

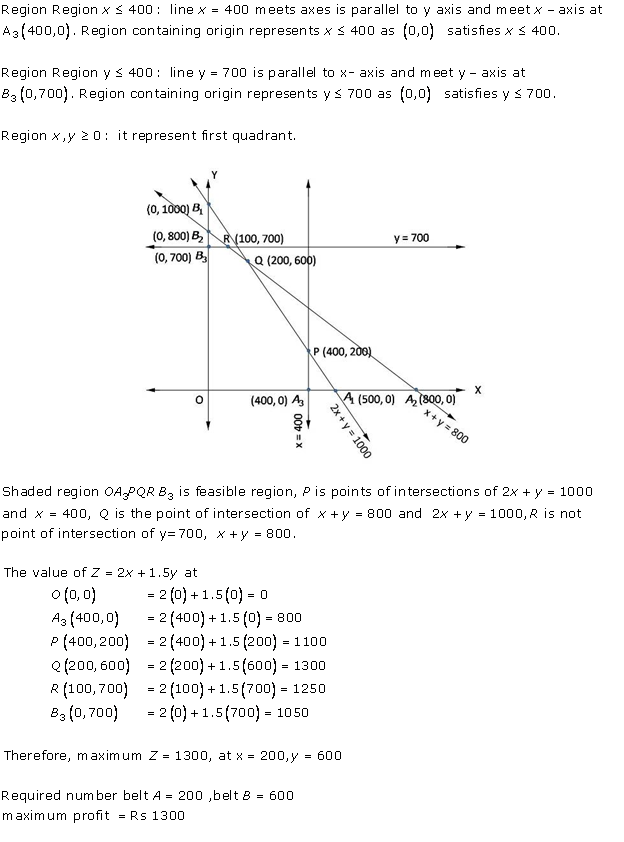
Solution 6

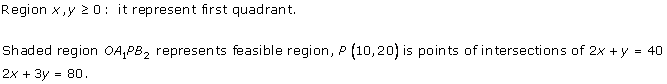

Solution 7

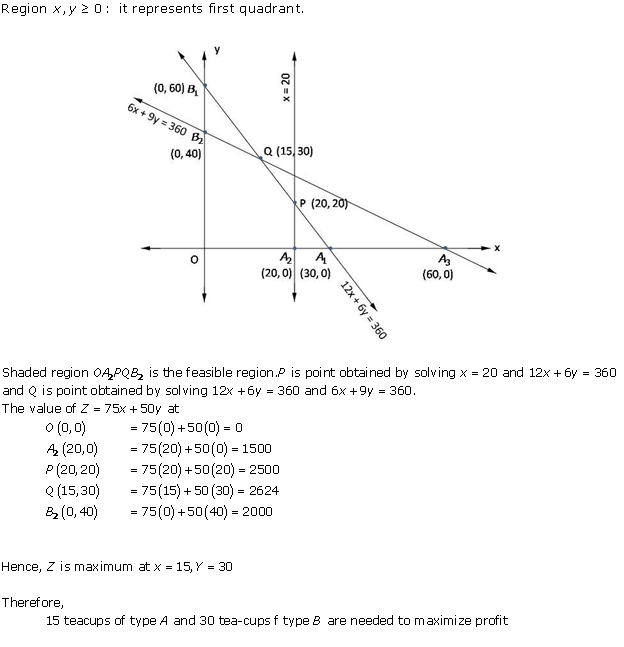
Solution 8

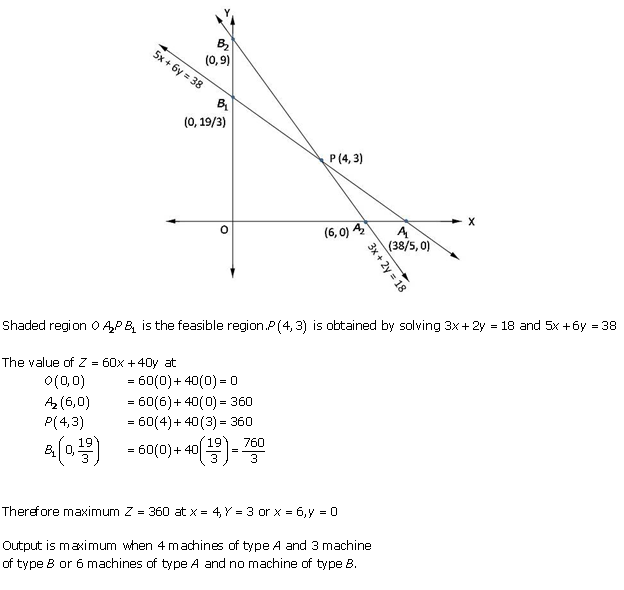
Solution 9


Solution 10

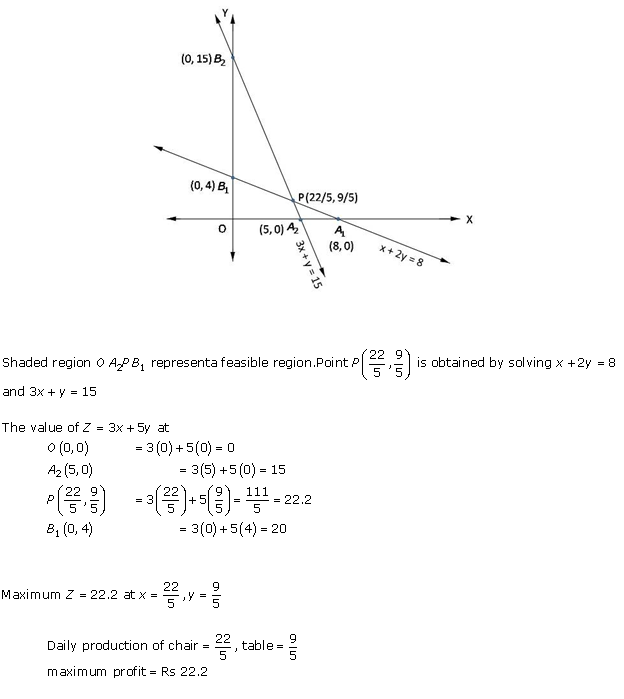
Solution 11

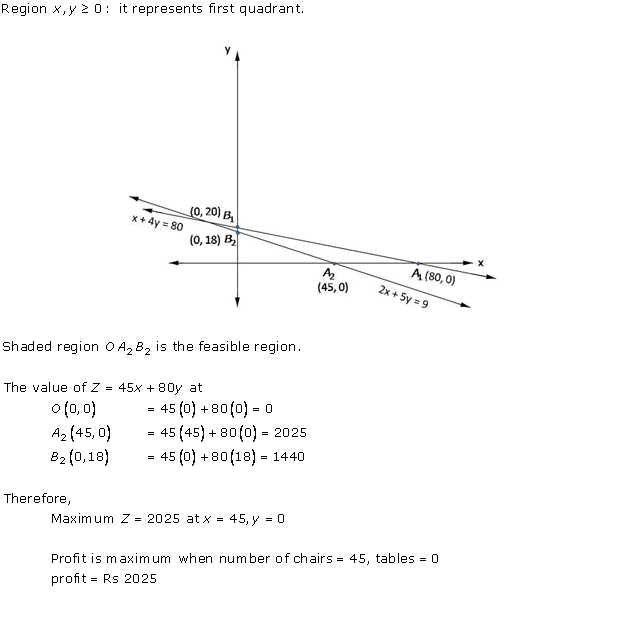
Solution 12


Solution 13
Solution 14

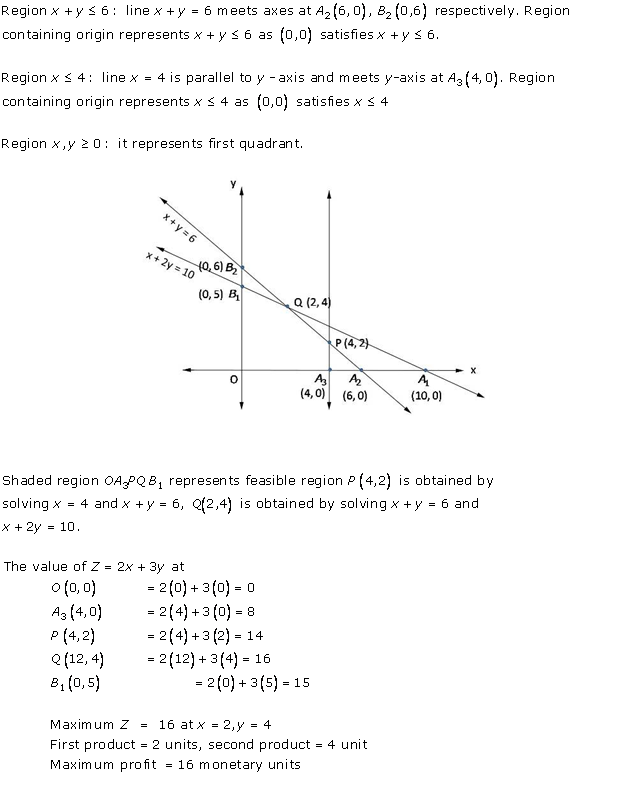
Solution 15
Solution 16
Solution 17

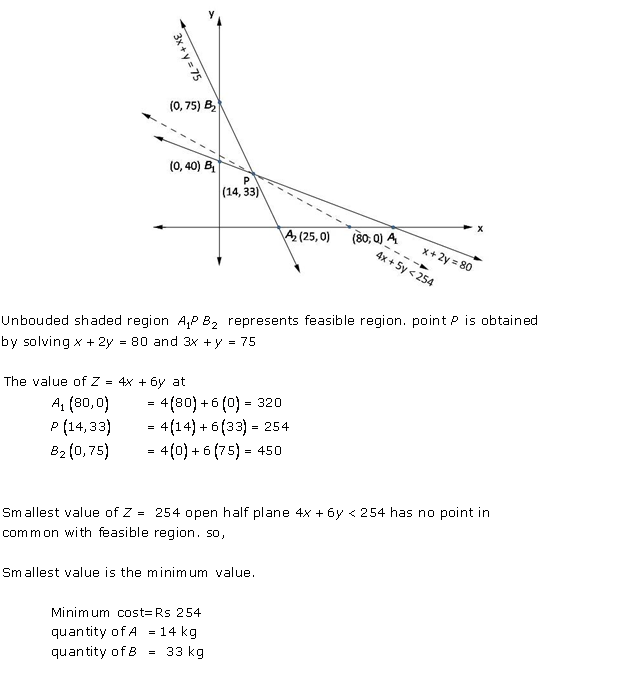
Solution 18
Solution 19



Solution 20

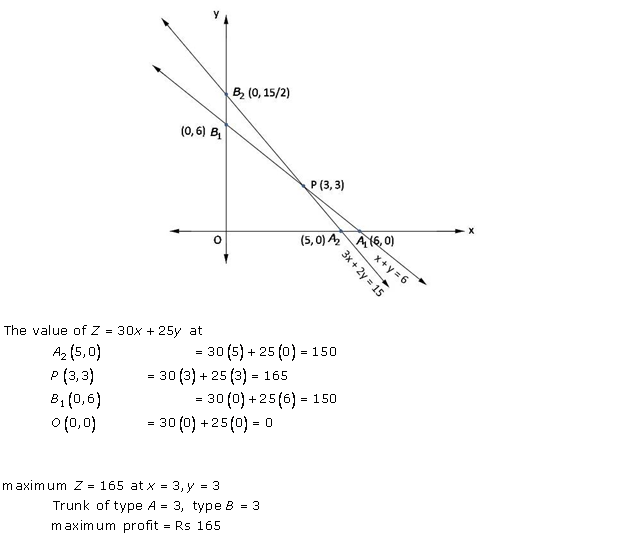
Solution 21

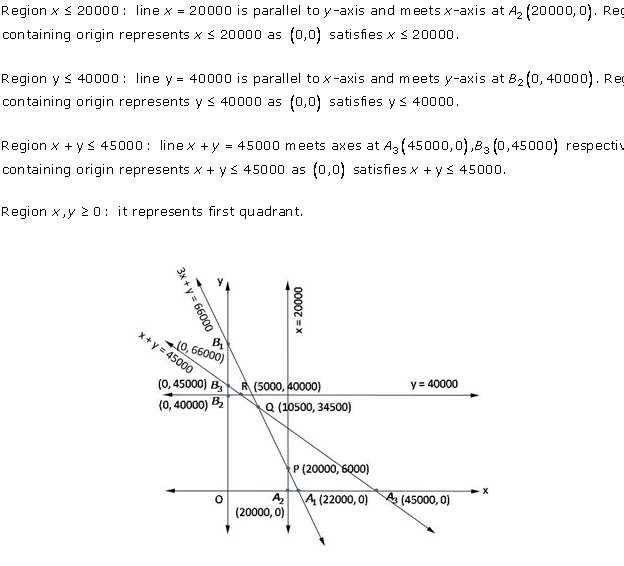

Solution 22


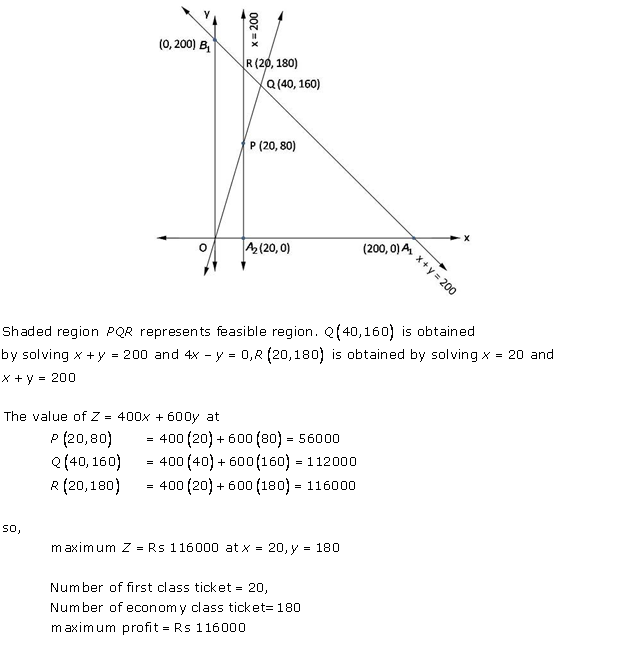
Solution 23
Solution 24

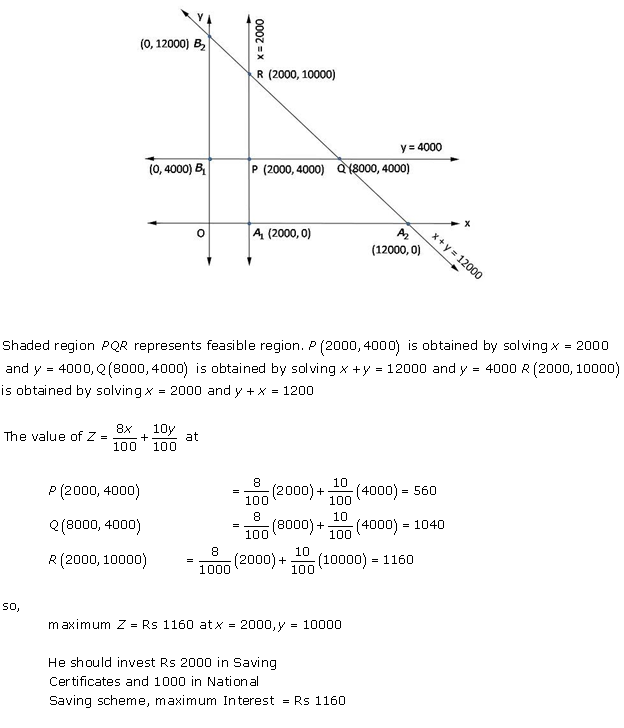
Solution 25

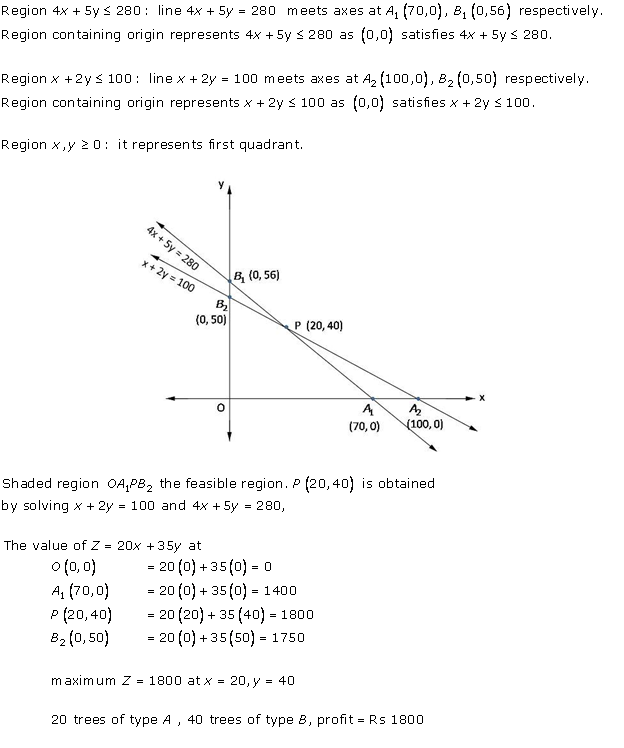
Solution 26
Solution 27


Solution 28

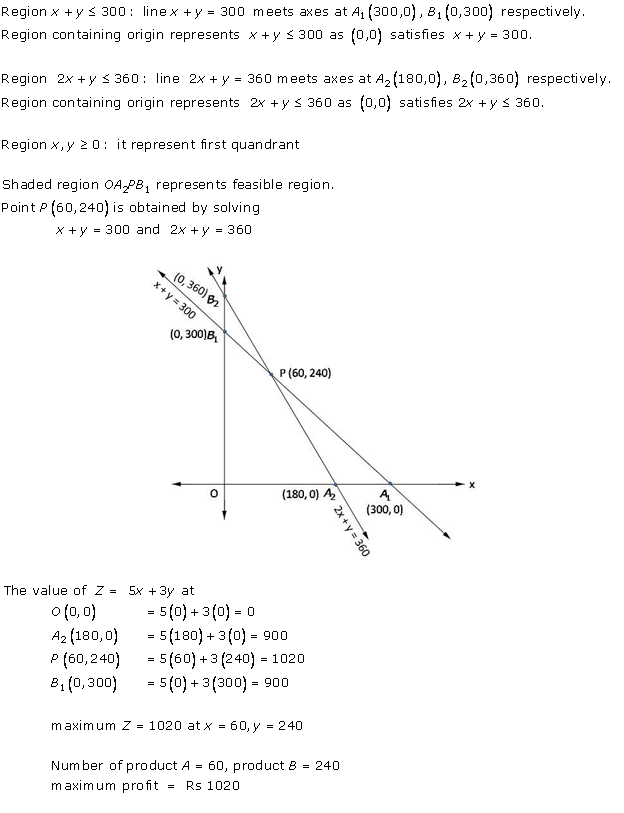
Solution 29

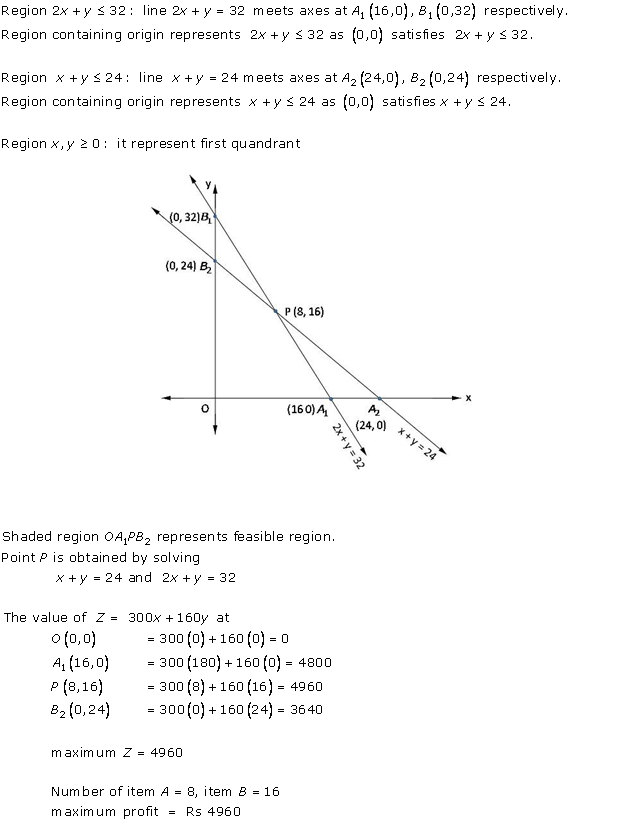
Solution 30

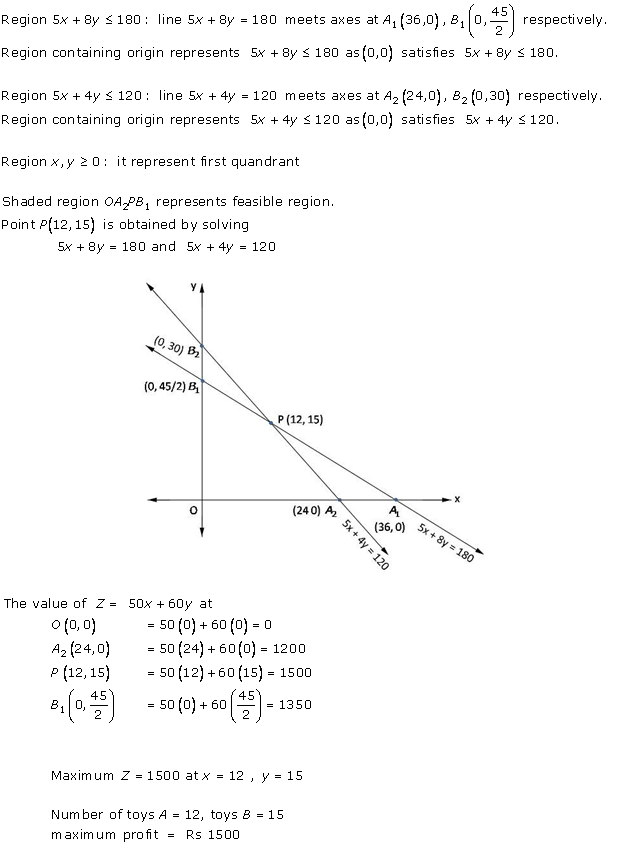
Solution 31

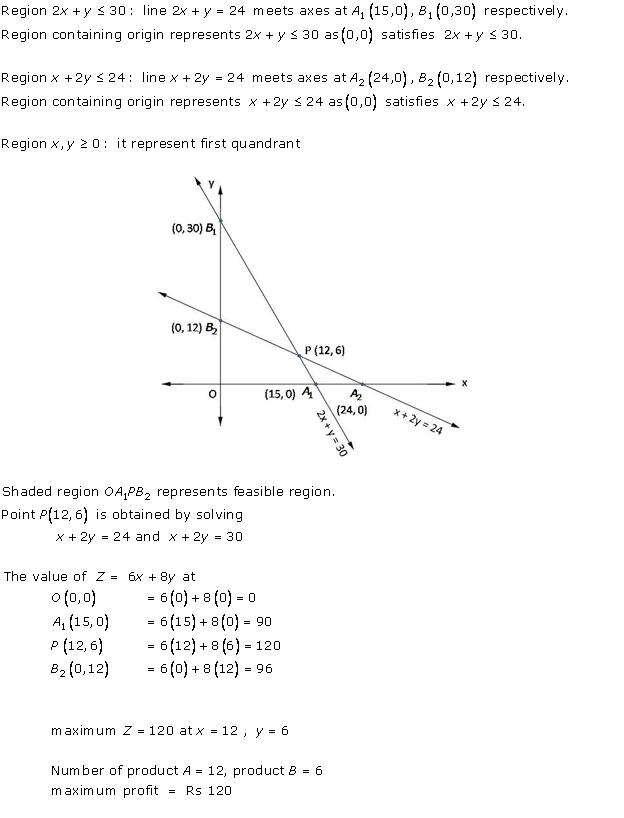
Solution 32
Solution 33



Solution 34


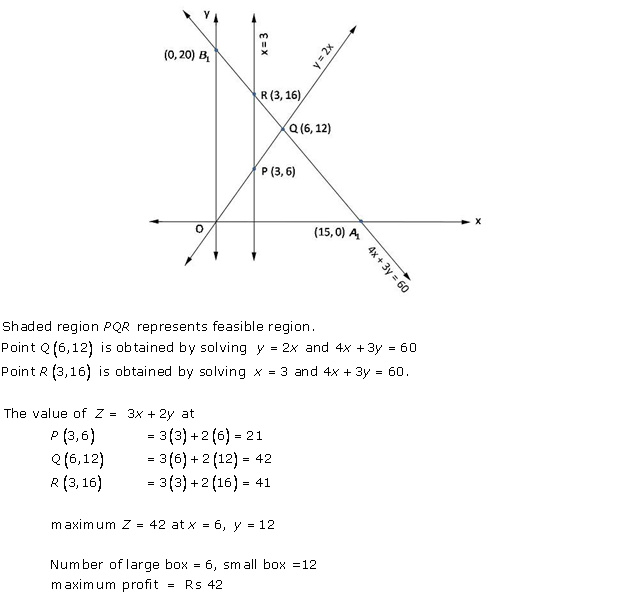
Solution 35


Solution 36

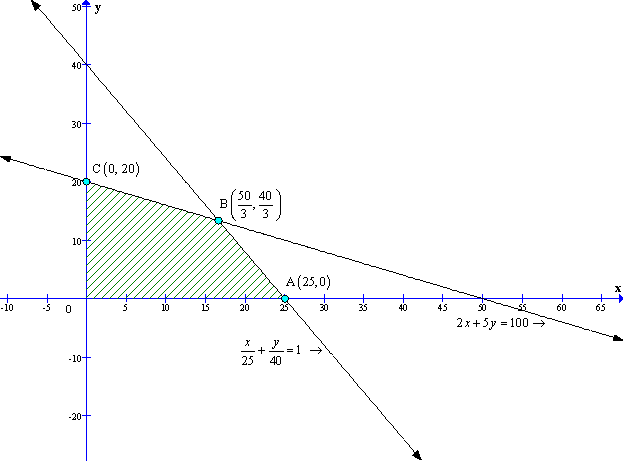

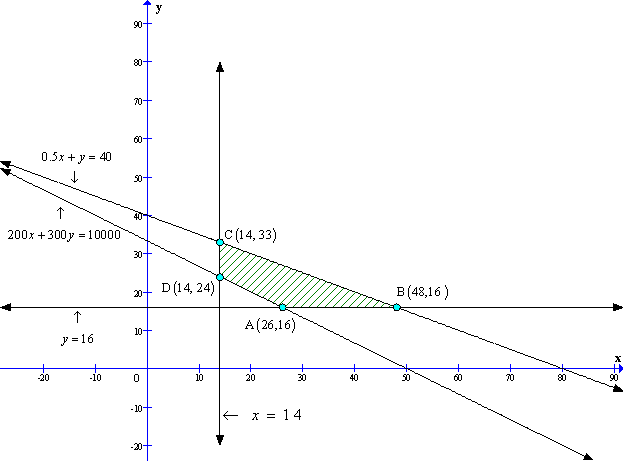
Solution 37
Solution 38

Solution 39


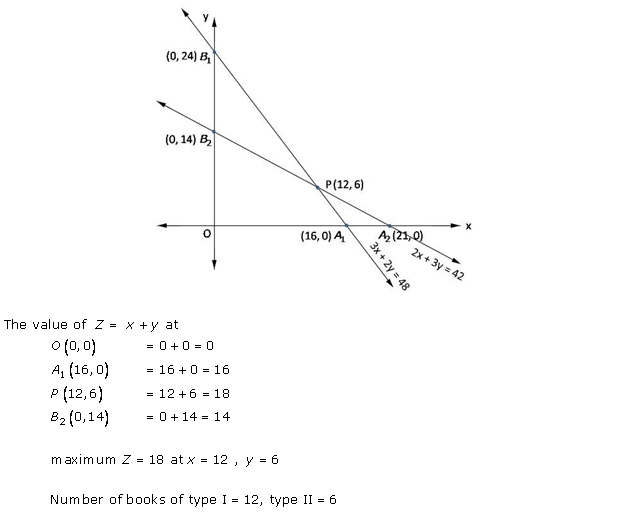
Solution 40
Solution 41
Solution 42

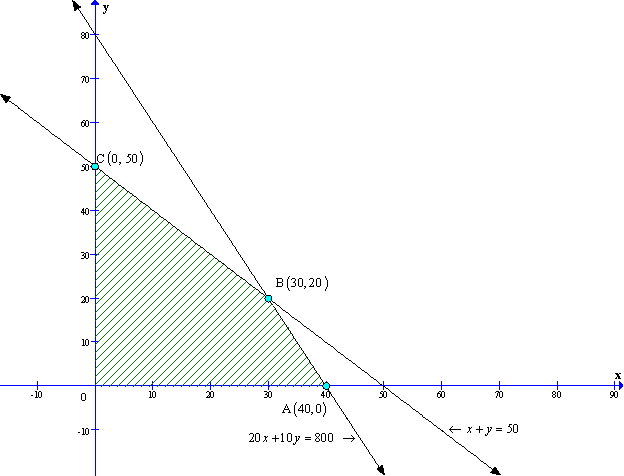

Solution 43

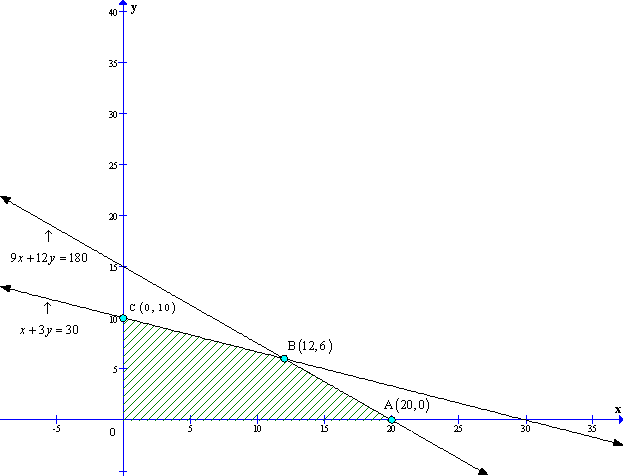

Solution 44

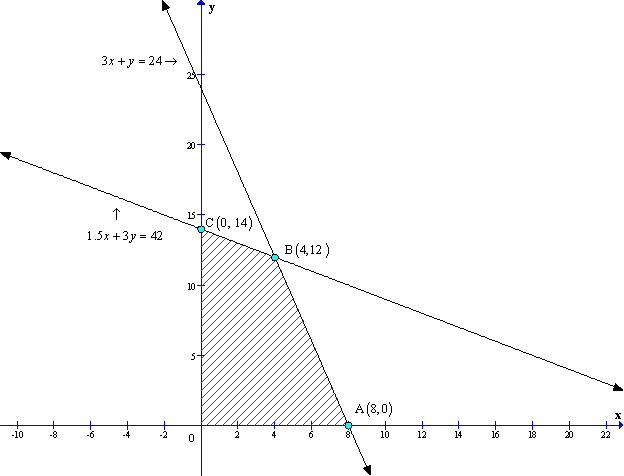

Solution 45

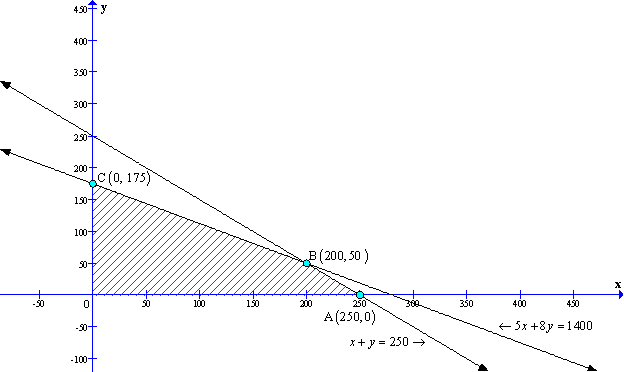

Solution 46

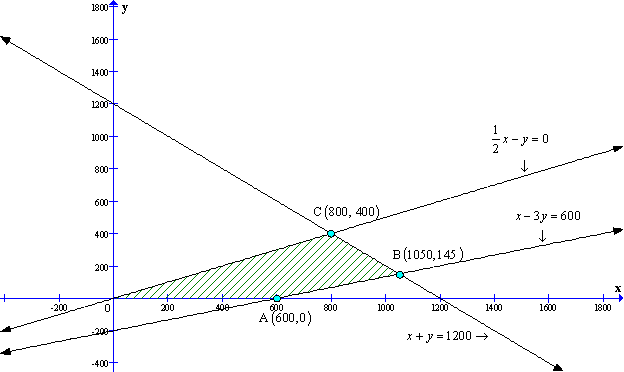

Solution 47



Solution 48

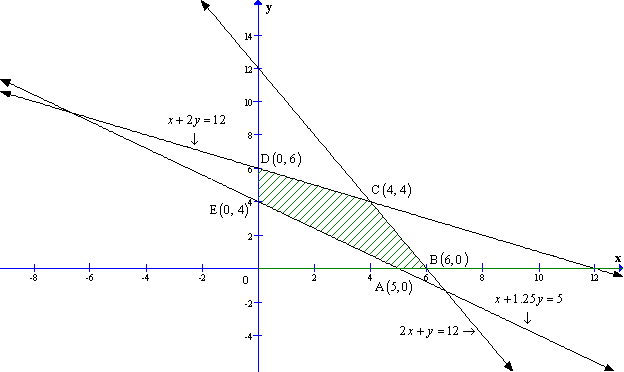

Solution 49
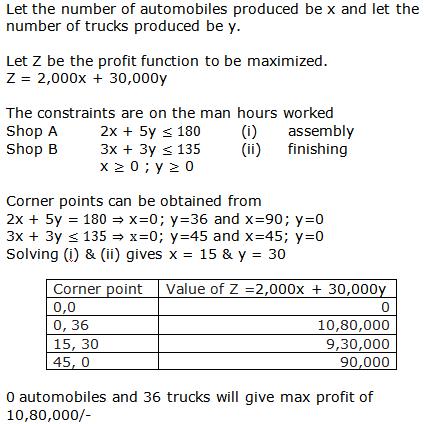
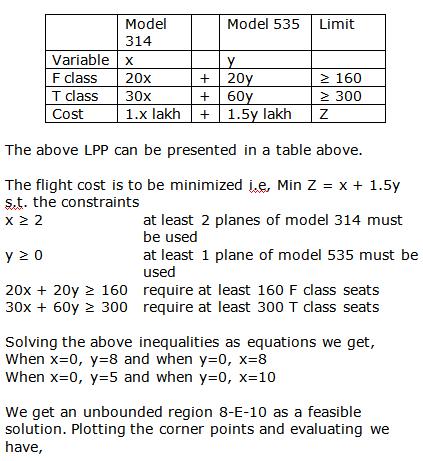
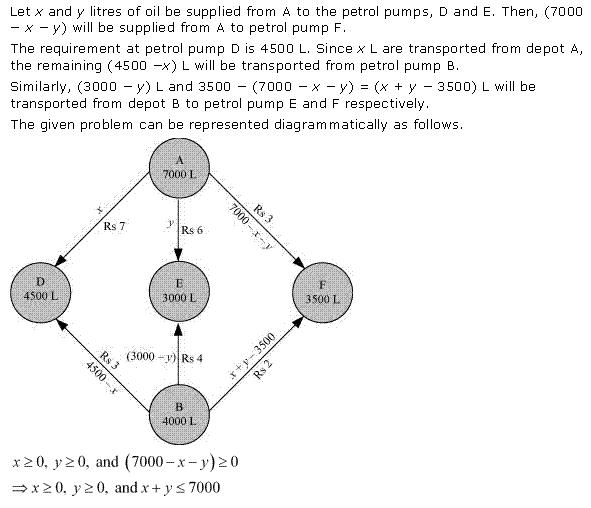
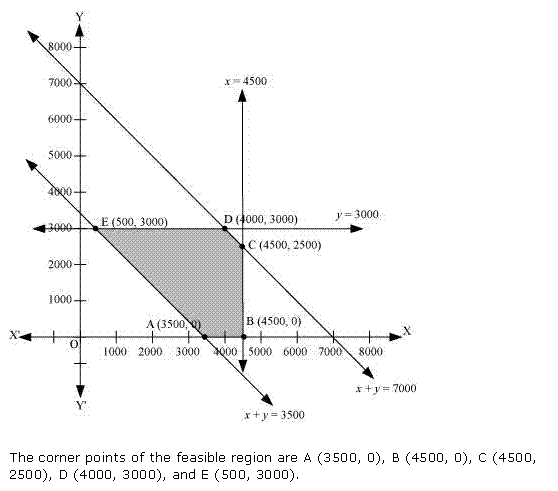
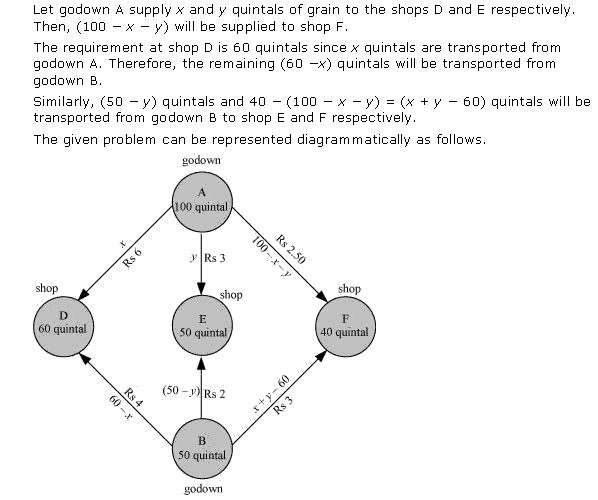
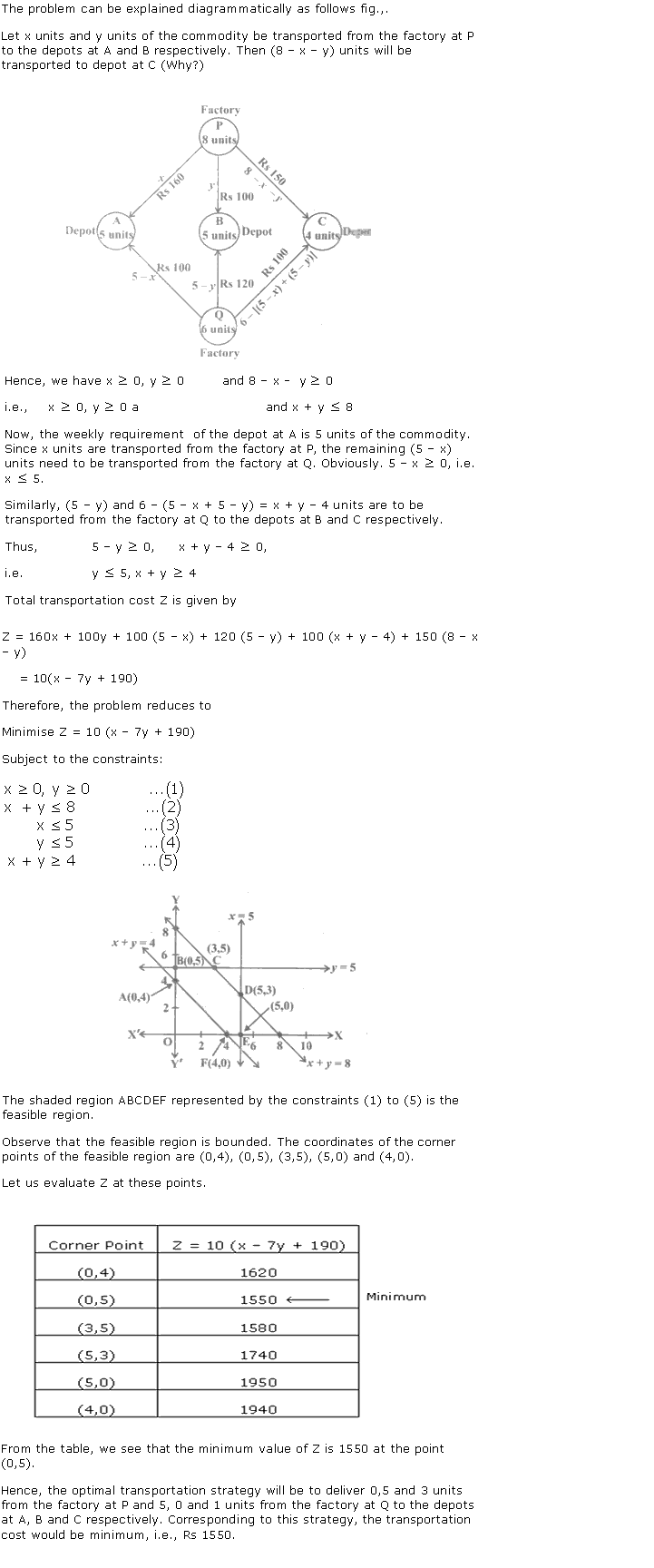
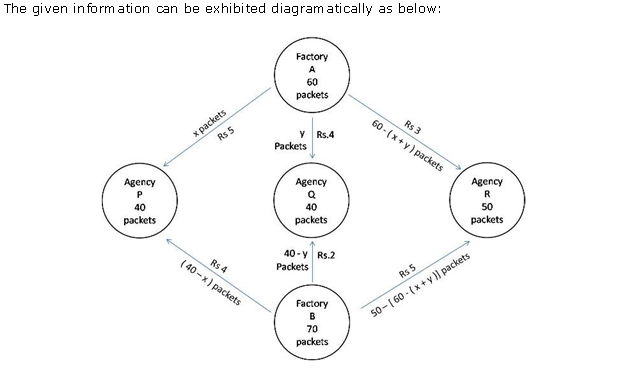
Let x and y units of commodity be transported from factory P to the depots at A and B respectively.
Then (8 - x - y) units will be transported to depot at C.
The flow is shown below.




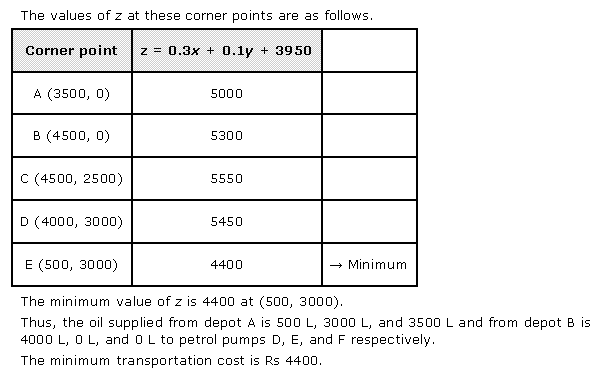
Solution 50

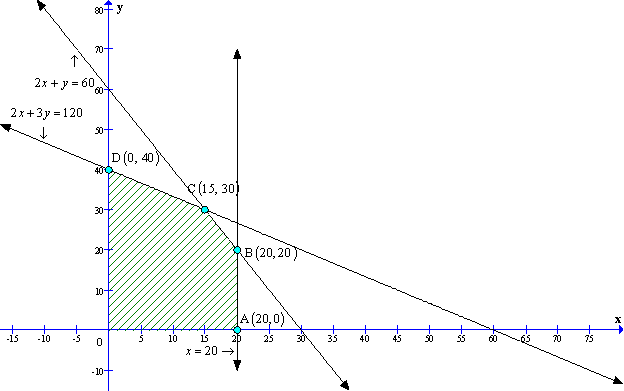

Solution 51

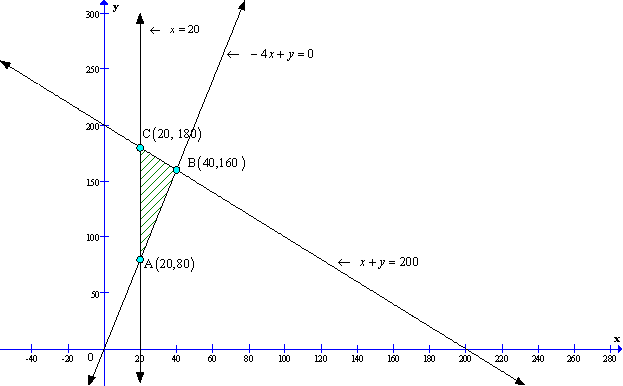
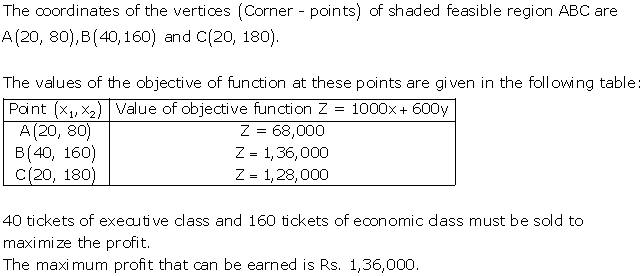
Solution 52


Linear programming Exercise Ex. 30.5
Solution 1
Solution 2

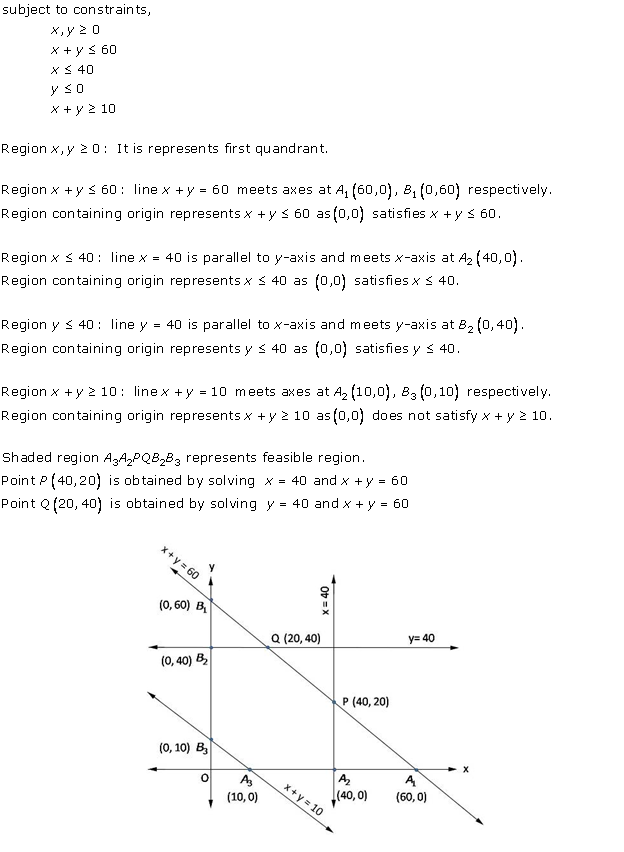

Linear programming Exercise Ex. 30RE
Solution 1(i)
Solution 1(ii)
Solution 1(iii)
Solution 1(iv)
Solution 1(v)

Solution 1(vi)

Solution 2
Solution 3
Solution 4
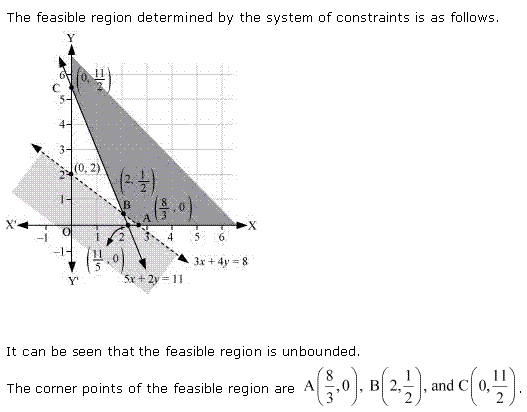

Solution 5
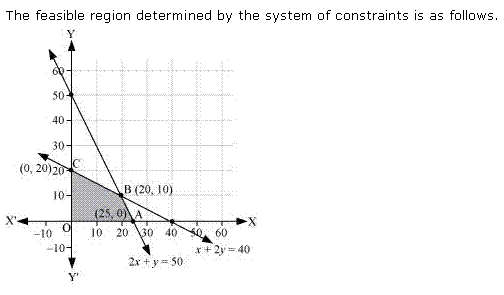
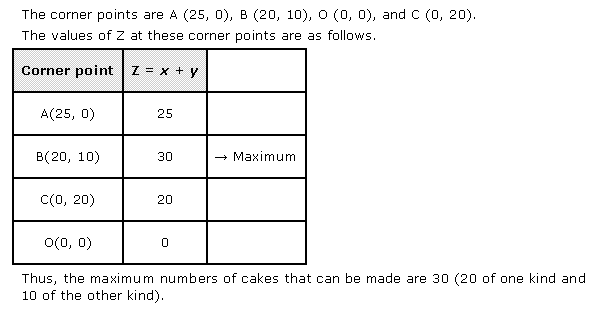
Solution 6
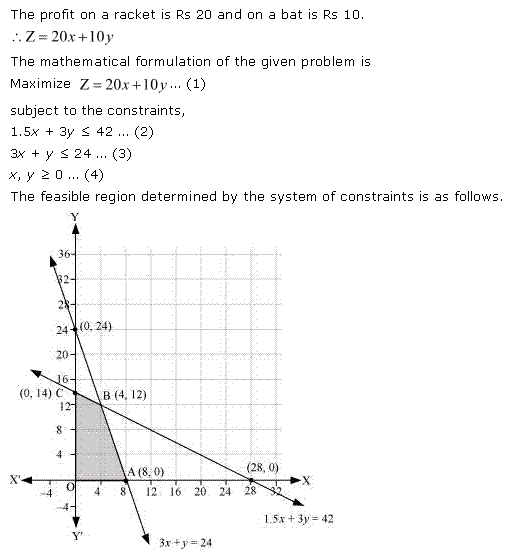
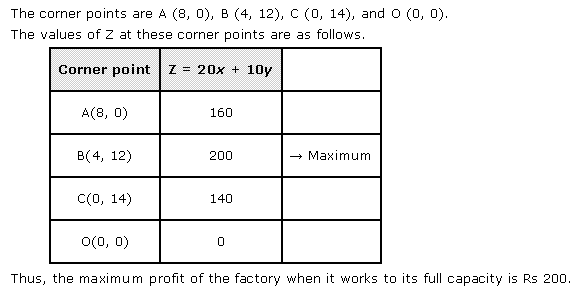
Solution 7

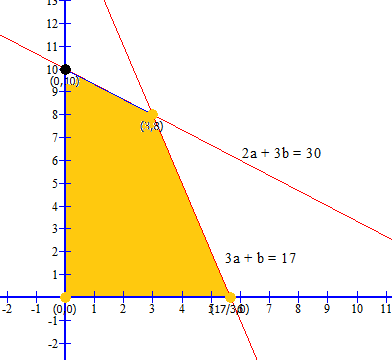
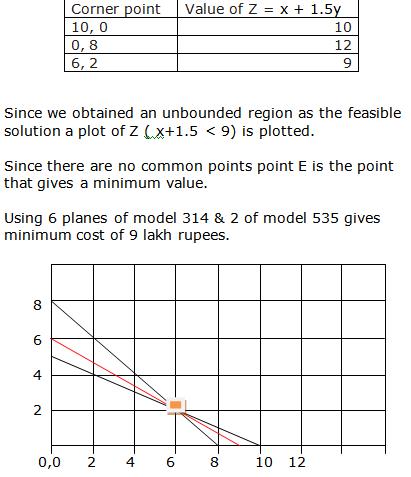
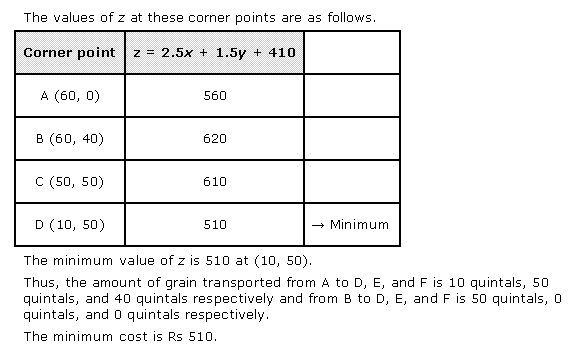
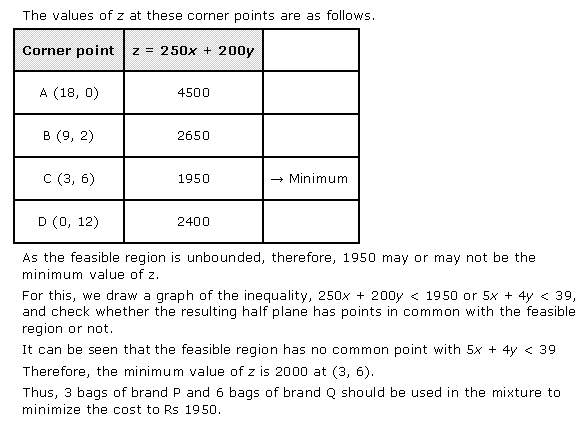
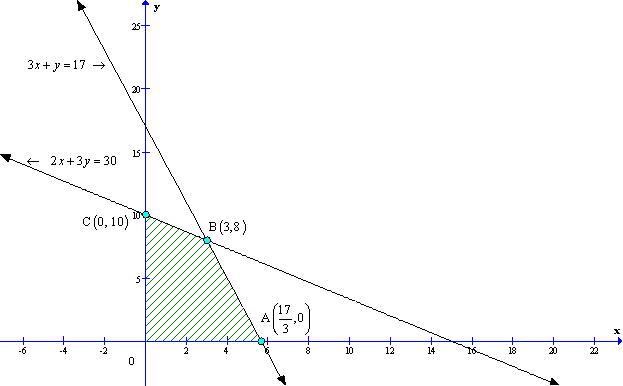
Corner points formed for:
|
Corner Points |
Profit |
Remarks |
|
(0, 0) |
Z = 100 × 0 + 120 × 0 = 0 |
|
|
(0, 10) |
Z = 100 × 0 + 120 × 10 = 1200 |
|
|
(3, 8) |
Z = 100 × 3 + 120 × 8 = 1260 |
Maximum |
|
(17/3, 0) |
Z = 100 × 17/3 + 120 × 0 = 1700/3 |
|
Revenue is maximum when x = 3, y = 8.
Maximum Profit = Rs. 1260
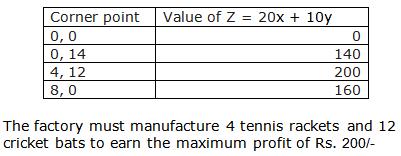
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
Solution 13
Solution 14
Solution 15
Solution 16
Solution 17
Solution 18
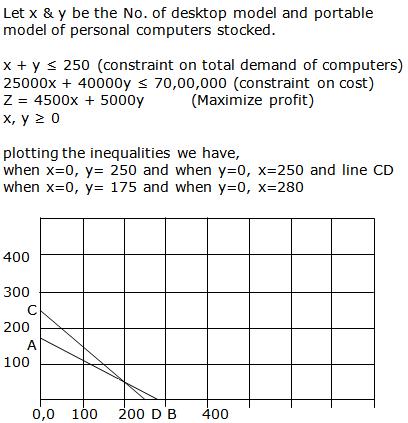
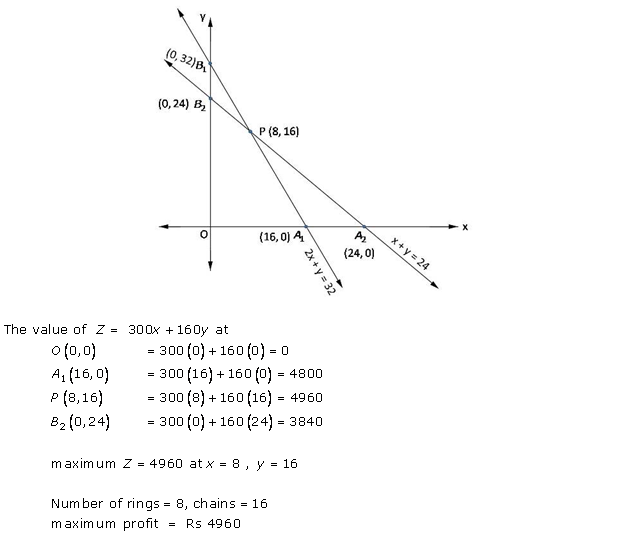
![]()

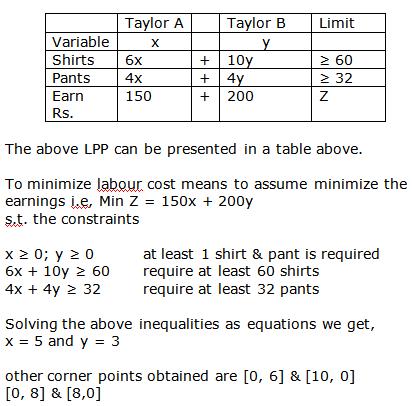
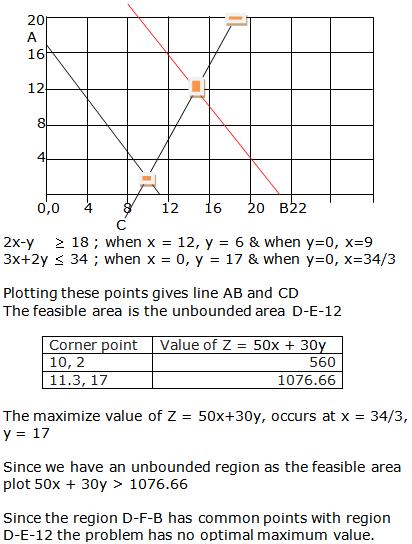
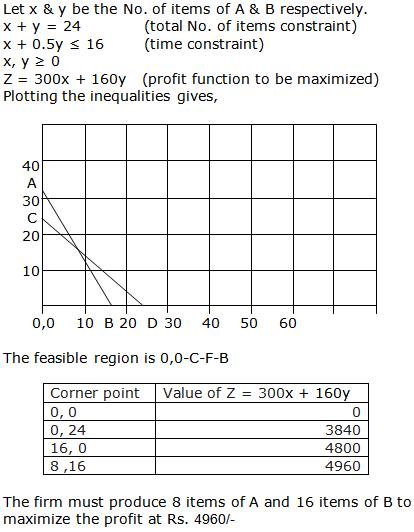
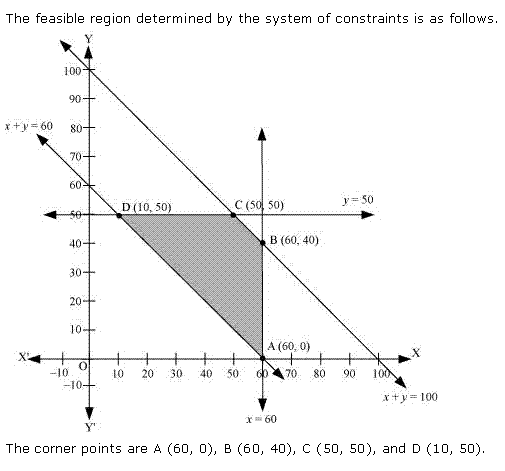
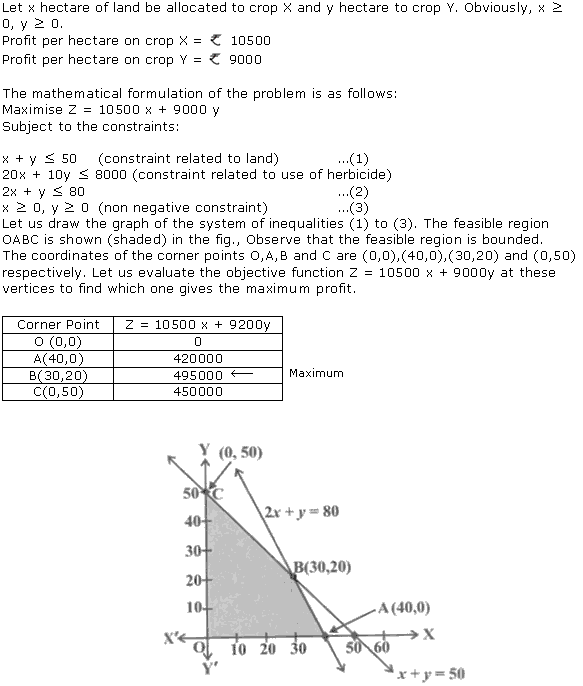
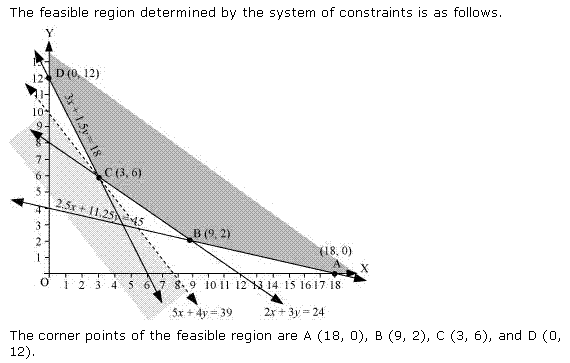
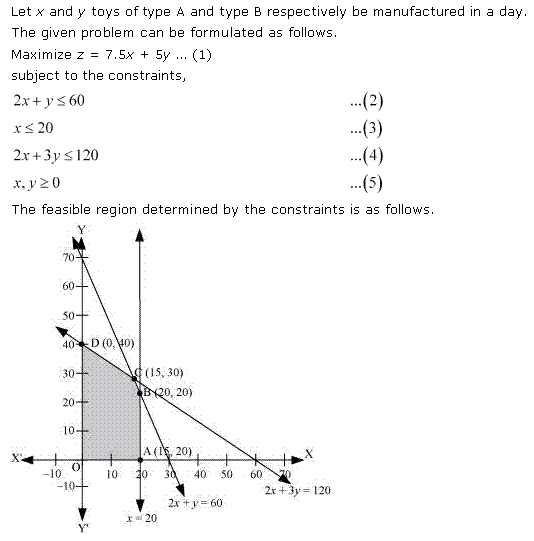
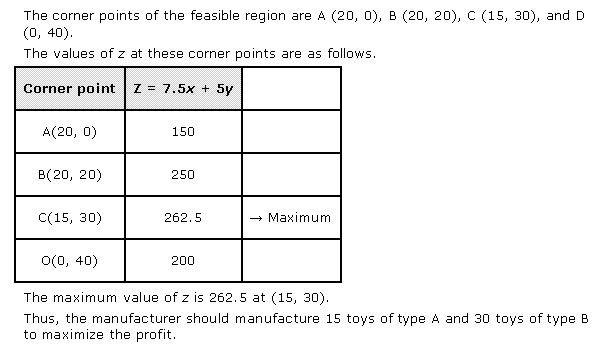
Let us plot the constraints and find the feasible region through graph.

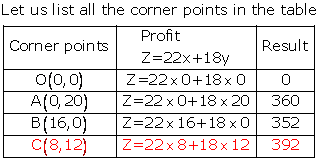
Thus the profit is maximum when the dealer buys 8 electronic sewing machines and 12 manual operated sewing machines.
Solution 19


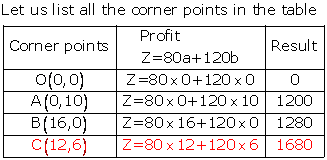
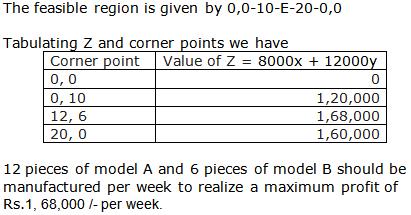
Thus profit is maximum and is equal to Rs.1680
The company should manufacture 12 Type A machines and 6 Type B machines to maximize their profit.
Linear programming Exercise MCQ
Solution 1
Correct option: (b)

Solution 2
Correct option: (b)
Objective function of a LPP is always maximized or minimized. Hence, it is optimized.
Solution 3
Correct option: (d)
Set of points between two parallel lines. Hence, set is connected. Set is convex.
Solution 4
Correct option: (b)

Solution 5
Correct option: (d)

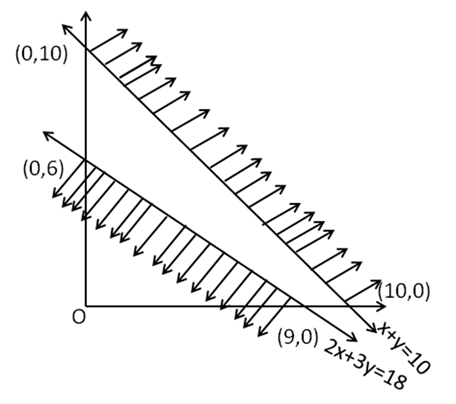
From the graph we conclude that no feasible region exist.
Solution 6
Correct option: (c)
The maximum value of the objective function is attained at the points given by corner points of the feasible region.
Solution 7
Correct option: (d)
If we put x=0 and y=0 in all the equations then we get contradiction. Hence, region is on open half plane not containing origin. The region is unbounded we can not find the maximum value of the feasible region.
Solution 8
Correct option: (c)

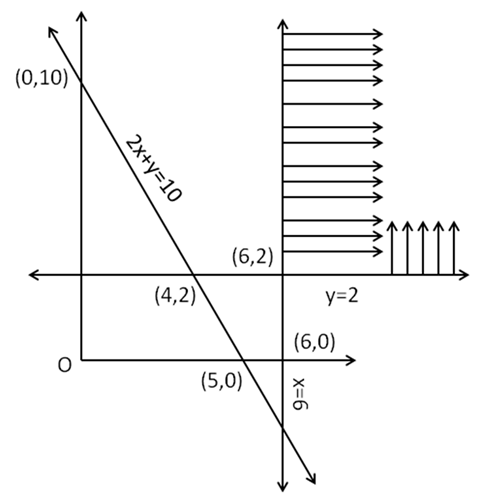
Minimum Z will be at 2x + y ≥ 10.
Solution 9
Correct option: (c)


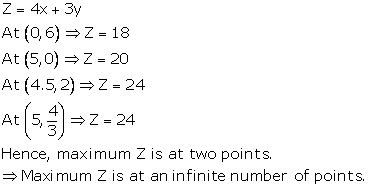
Solution 10
Correct option: (a)
Optimization of objective function is depend on constraints. Hence, if the constraints in a linear programming problem are changed the problem is to be re-evaluated.
Solution 11
Correct option: (c)
Optimal solution of LPP has three types.
- Unique
- Infinite
- Does not exist.
Hence, it has infinite solution if it admits two optimal solution.
Solution 12
Correct option: (c)
As |x|=5 will only on x-axis. Hence, set is not connected to any two points between the set.
Hence, it is not convex.
Solution 13
Correct option: (b)
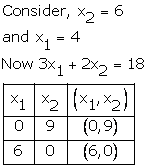
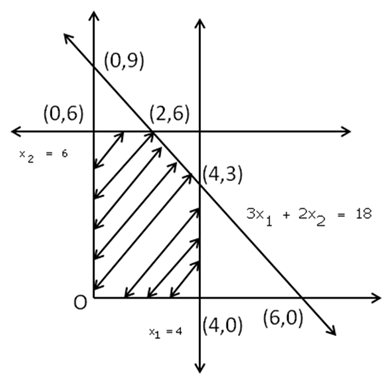

Solution 14
Correct option: (c)
As region is on origin side it is always bounded. Also, given that x,y ≥ 0 it is bounded in the first quadrant.
NOTE: Answer not matching with back answer.
Solution 15
Correct option: (d)



Solution 16
Correct option: (c)
To find maximum or minimum value of the region we use the coordinates of the vertices of feasible region. Hence, the value of objective function is maximum under linear constraints at any vertex of the feasible region.
Note: Answer not matching with back answer.
Solution 17
Correct option: (d)
Given that Z=px + qy
Maximum value at (3, 4) = maximum value at (0, 5)
3p+4q=5q
q=3p