Class 12-science RD SHARMA Solutions Maths Chapter 27 - Direction Cosines and Direction Ratios
Direction Cosines and Direction Ratios Exercise Ex. 27.1
Solution 1
Let l, m and n be the direction cosines of a line.
l = cos 90° = 0
![]()
![]()
![]()
Solution 2

Solution 3

Solution 4

Solution 5

Solution 6
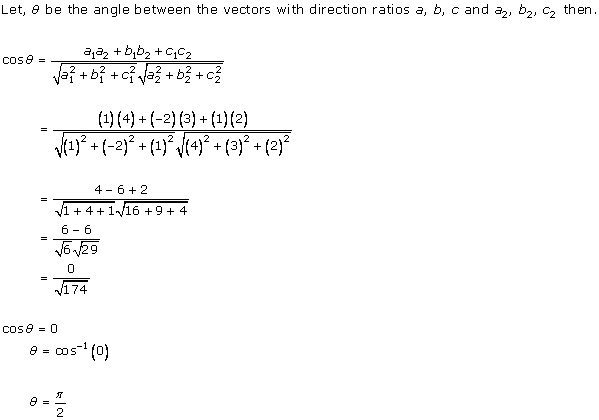
Solution 7
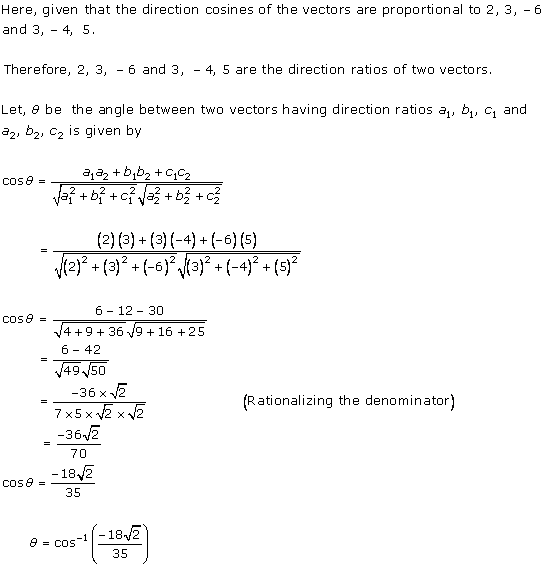
Solution 8
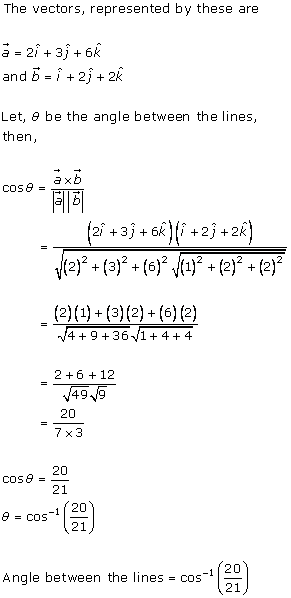
Solution 9

Solution 10
Solution 11

Solution 12
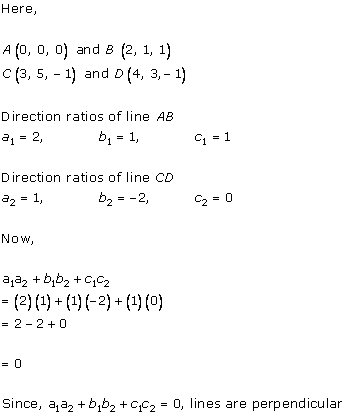
Solution 13
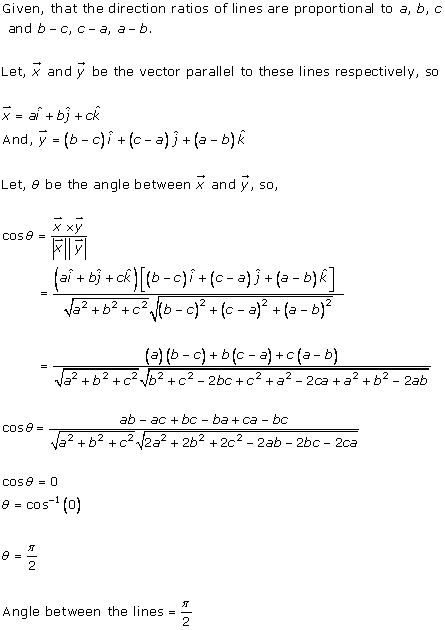
Solution 14

Solution 15
Solution 16(i)

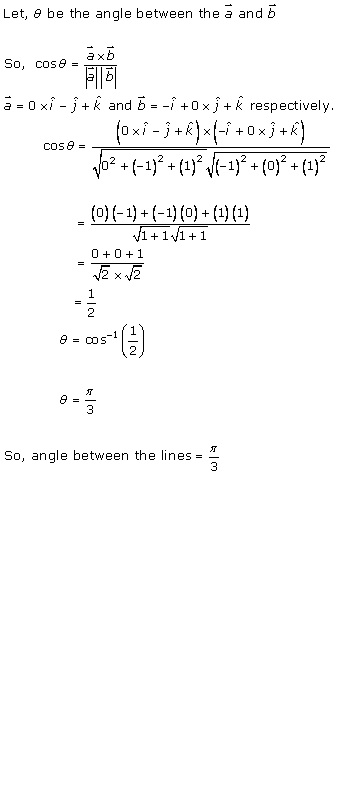
Solution 16(ii)

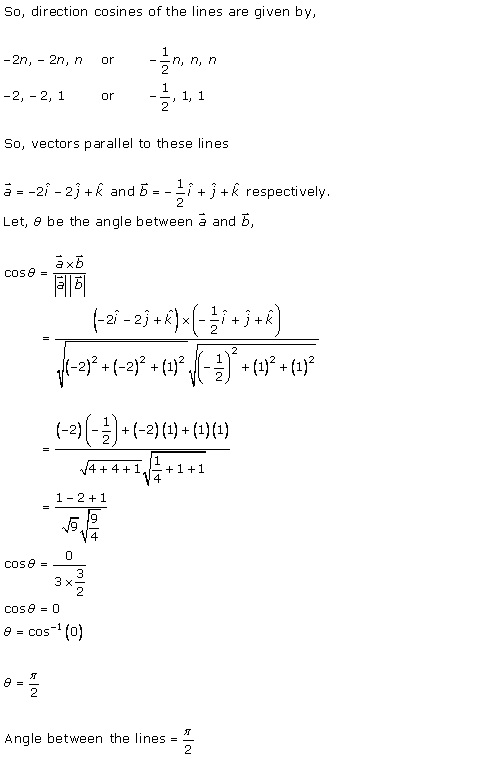
Solution 16(iii)
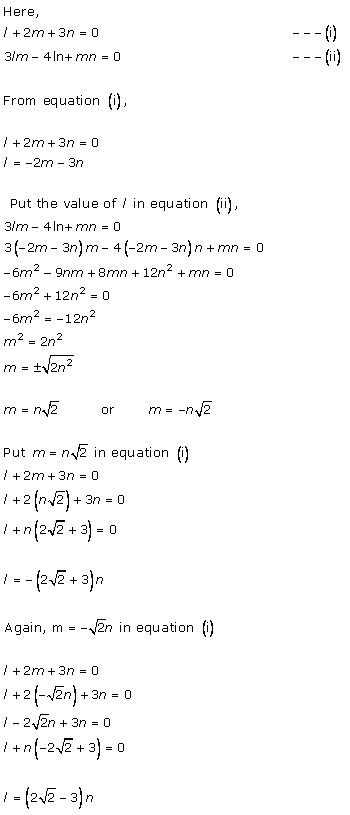

Solution 16(iv)

Direction Cosines and Direction Ratios Exercise MCQ
Solution 1
Correct option: (c)
Every point on xy-plane z co-ordinate is always zero.
Solution 2
Correct option: (c)
Point (x, y, z) is on the x-axis. Hence, y and z co-ordinate will be zero except the origin.
Solution 3
Correct option: (d)
Coordinates of the points given are diagonally opposite vertices of a parallelepiped. Hence, edges of parallelepiped can be 5-2, 7-3, 9-7 ⇒3,4,2.
Solution 4
Correct option : (a)
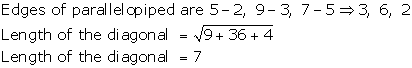
Solution 5
Correct option: (b)

Solution 6
Correct option: (c)

Solution 7
Correct option: (a)

Solution 8
Correct option: (b)

Solution 9
Correct option: (b)

Solution 10
Correct option: (a)

Solution 11
Correct option: (a)
Directions of OP from the origin
(-1,2,-2)=(x,y,z)
Solution 12
Correct option: (d)
![]()
Solution 13
Correct option: (c)
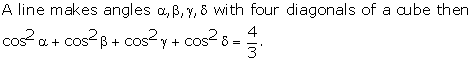
Direction Cosines and Direction Ratios Exercise Ex. 27VSAQ
Solution 1

Solution 2

Solution 3

Solution 4

Solution 5

Solution 6

Solution 7

Solution 8
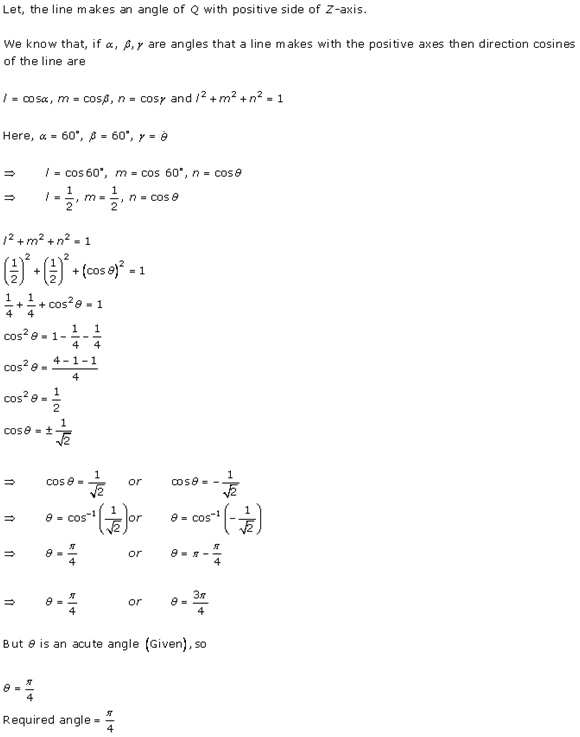
Solution 9

Solution 10

Solution 11

Solution 12

Solution 13
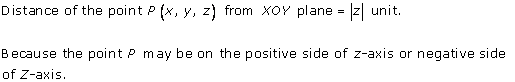
Solution 14
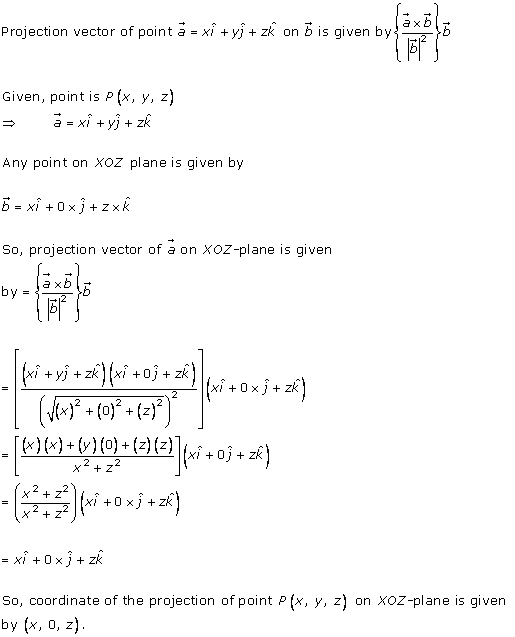
Solution 15

So the projection of the point P on y-axis is (0, -3, 0)
Solution 16

Solution 17
Solution 18
Solution 19
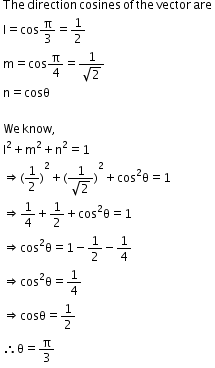
Solution 20