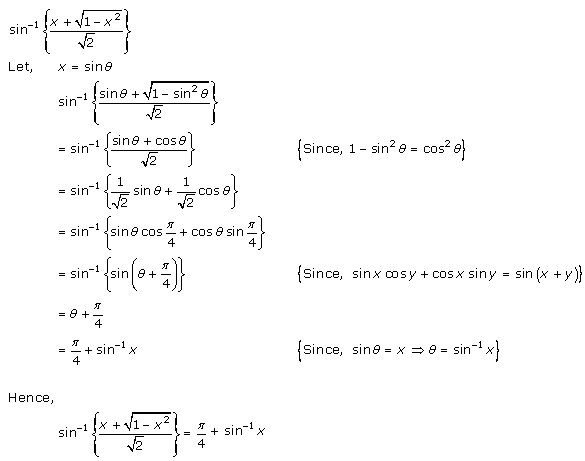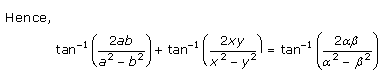Class 12-commerce RD SHARMA Solutions Maths Chapter 4: Inverse Trigonometric Functions
Inverse Trigonometric Functions Exercise Ex. 4.1
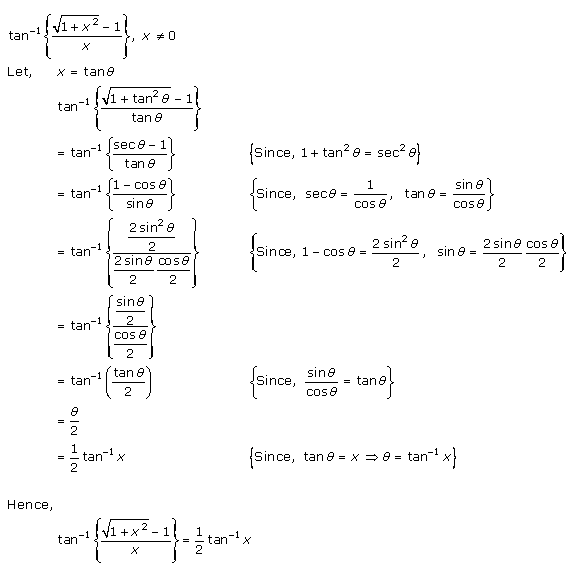
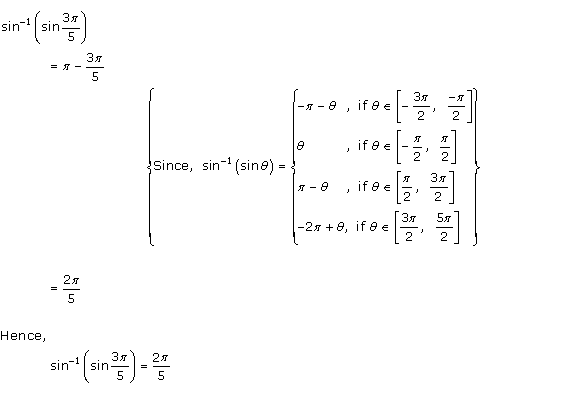
Solution 1(i)
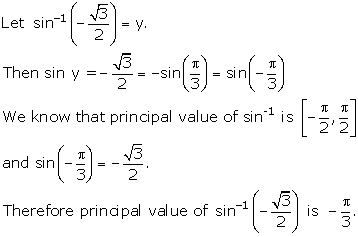
Solution 1(ii)
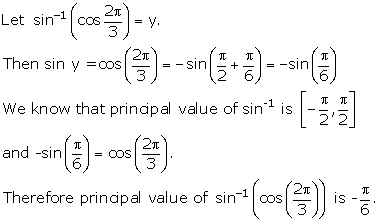
Solution 1(iii)
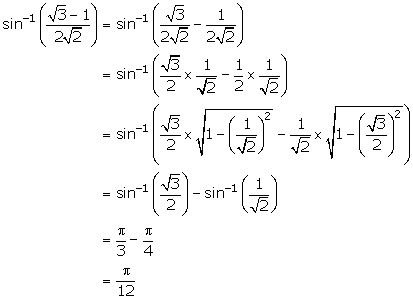
Solution 1(iv)
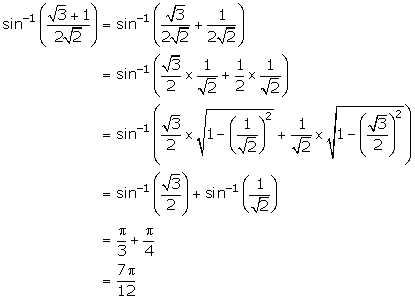
Solution 1(v)
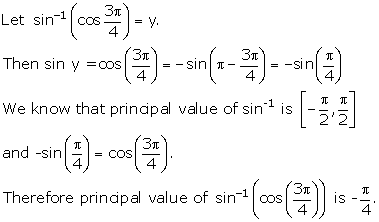
Solution 1(vi)
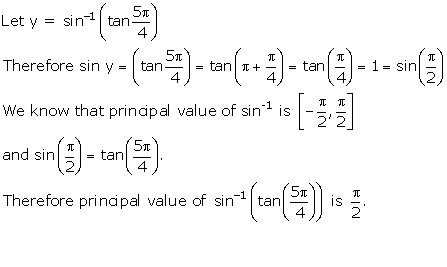
Solution 2(i)
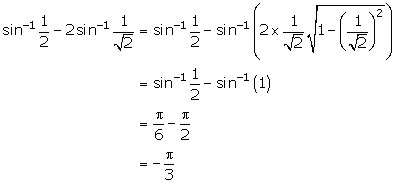
Solution 2(ii)
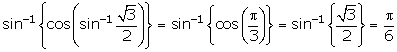
Solution 3(i)
Solution 3(ii)
Solution 3(iii)
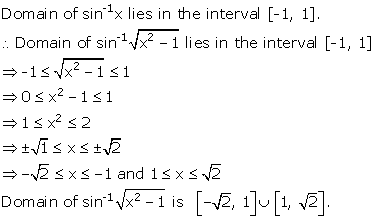
Solution 3(iv)
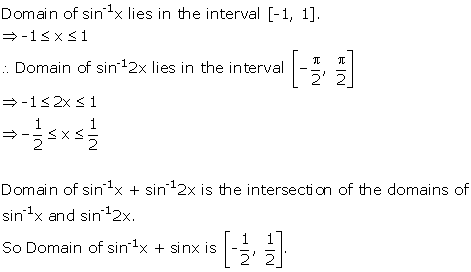
Solution 4
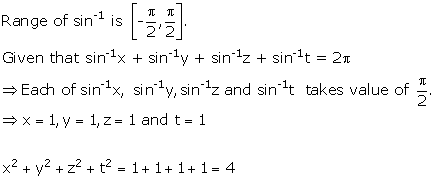
Solution 5
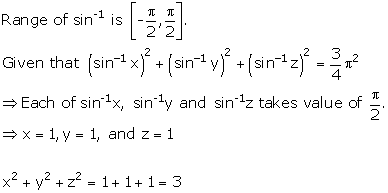
Inverse Trigonometric Functions Exercise Ex. 4.2
Solution 1
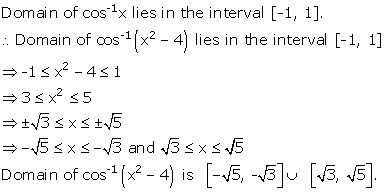
Solution 2
Solution 3
Solution 4(i)
Solution 4(ii)
Solution 4(iii)
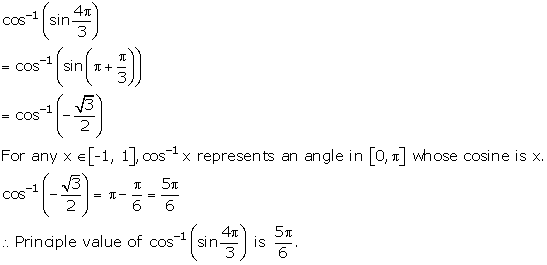
Solution 4(iv)
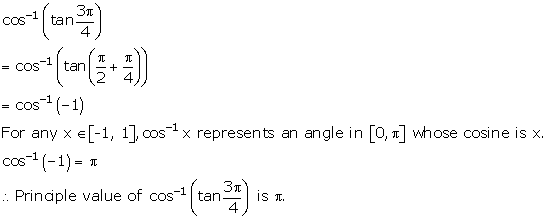
Solution 5(i)
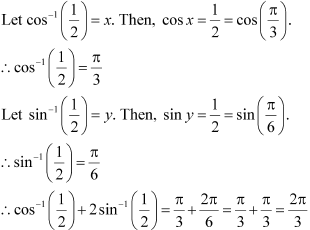
Solution 5(ii)
Solution 5(iii)
?
Solution 5(iv)
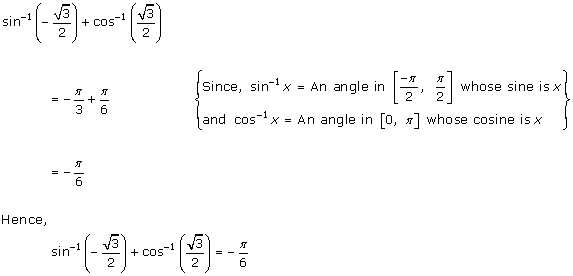
Inverse Trigonometric Functions Exercise Ex. 4.3
Solution 1(i)
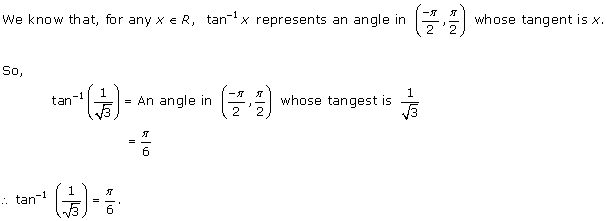
Solution 1(ii)
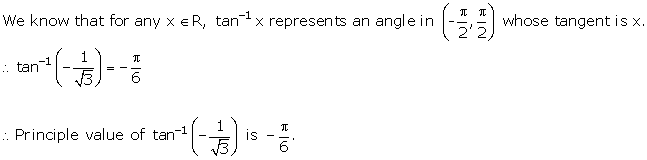
Solution 1(iii)
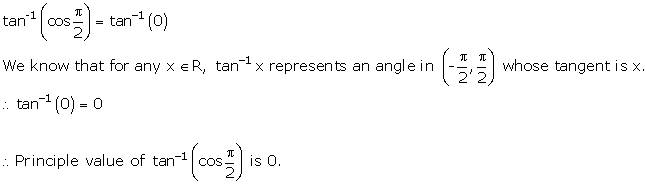
Solution 1(iv)
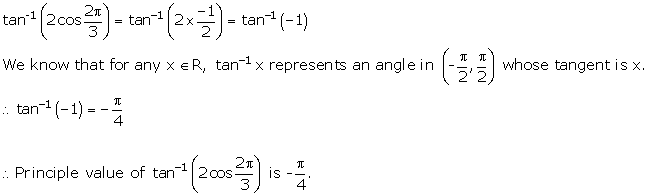
Solution 2(i)
Solution 2(ii)
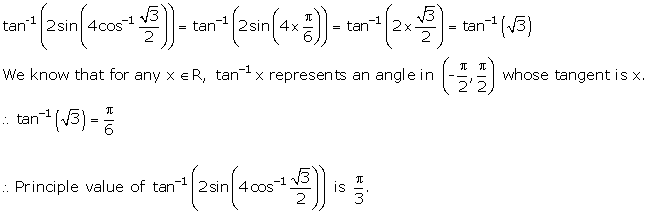
Solution 3(i)
Solution 3(ii)
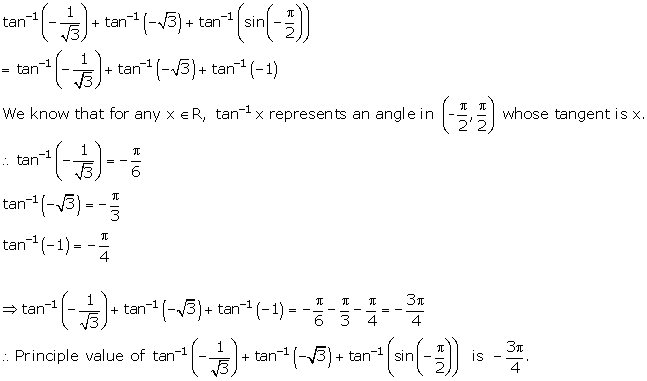
Solution 3(iii)
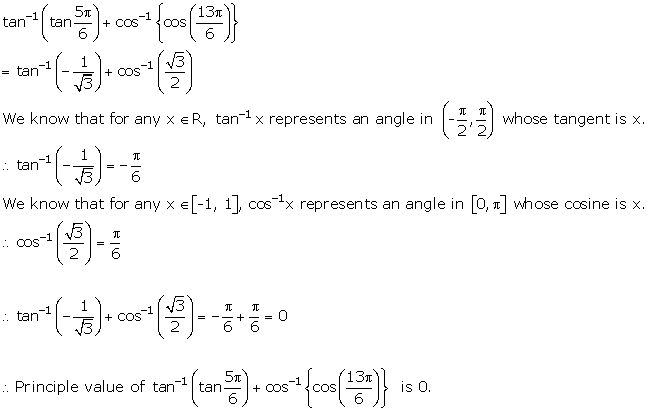
Inverse Trigonometric Functions Exercise Ex. 4.4
Solution 1(i)
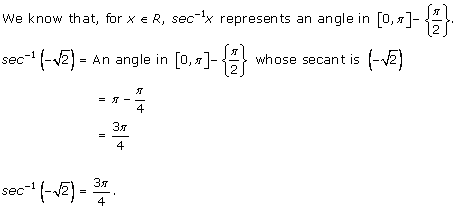
Solution 1(ii)
Solution 1(iii)
Solution 1(iv)
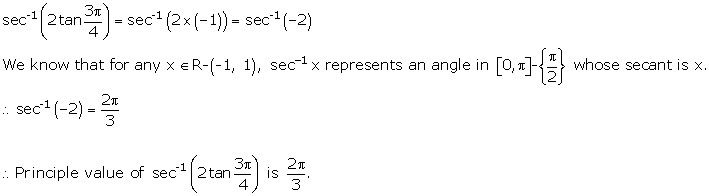
Solution 2(i)
Solution 2(ii)
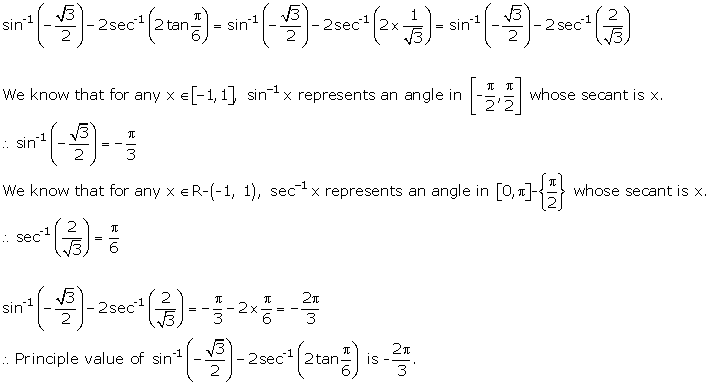
Solution 3(i)
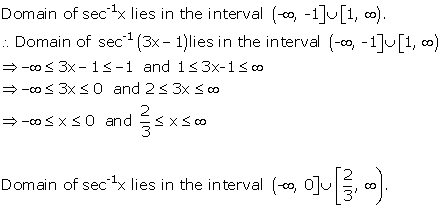
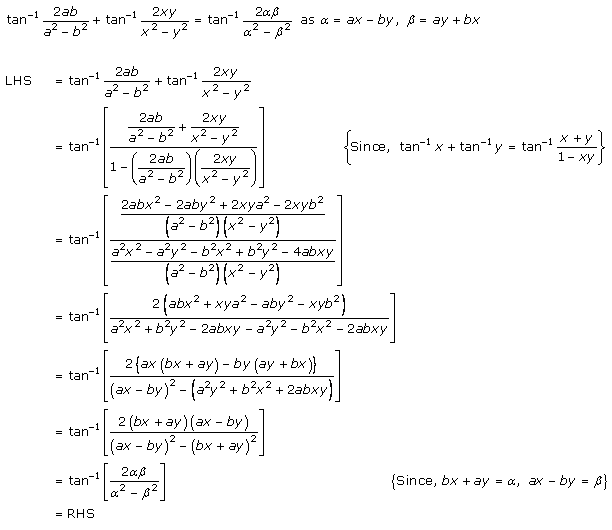
Solution 3(ii)
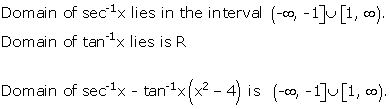
Inverse Trigonometric Functions Exercise Ex. 4.5
Solution 1(i)
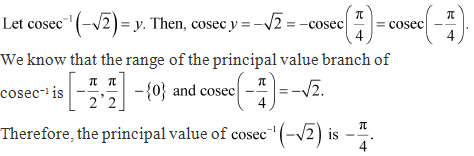
Solution 1(ii)
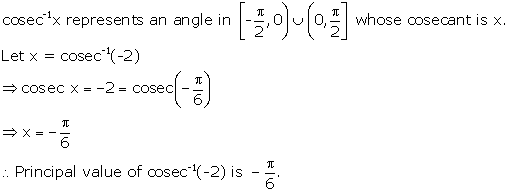
Solution 1(iii)
Solution 1(iv)
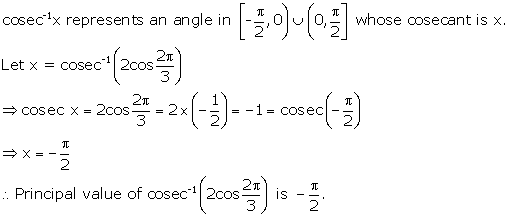
Solution 2
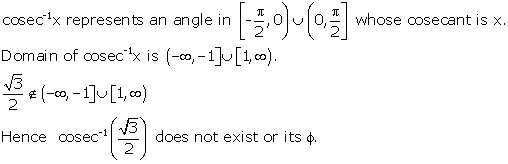
Solution 3(i)
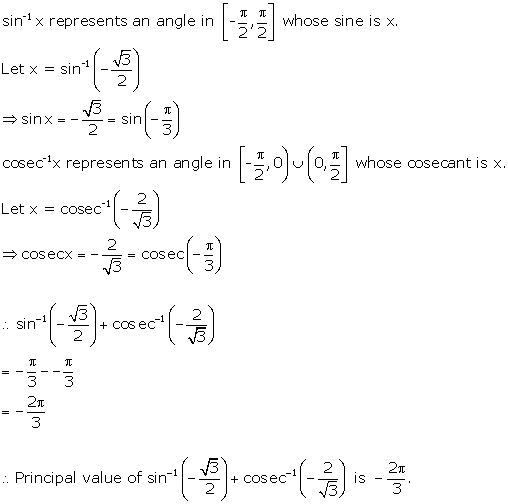
Solution 3(ii)
Solution 3(iii)
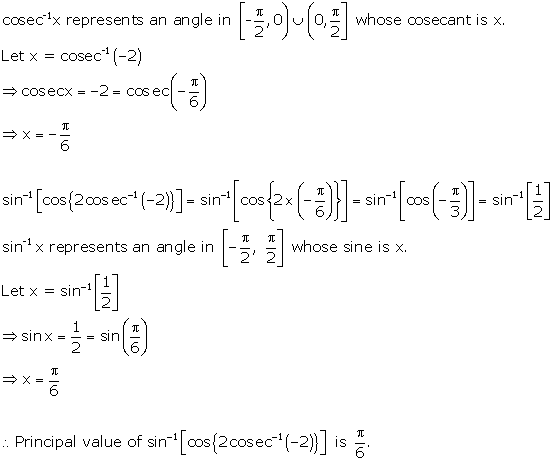
Solution 3(iv)
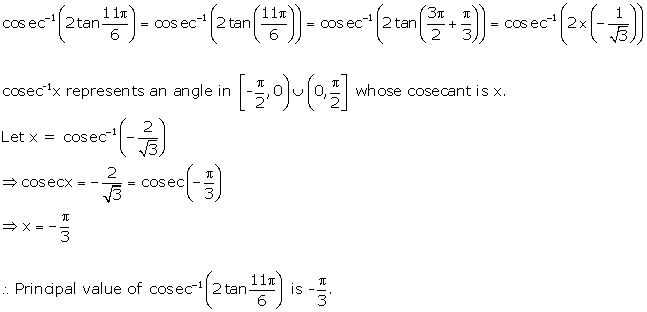
Inverse Trigonometric Functions Exercise Ex. 4.6
Solution 1(i)
Solution 1(ii)
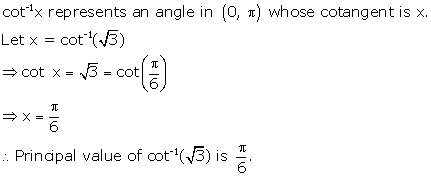
Solution 1(iii)
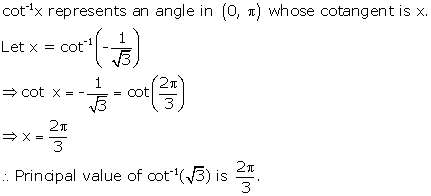
Solution 1(iv)
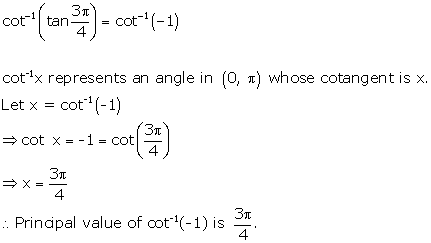
Solution 2
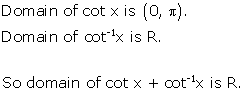
Solution 3(i)
Solution 3(ii)
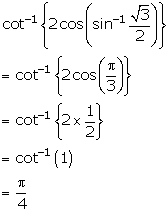
Solution 3(iii)
Solution 3(iv)
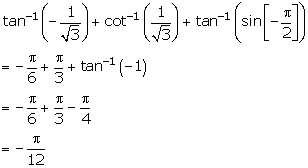
Inverse Trigonometric Functions Exercise Ex. 4.7
Solution 1(i)
We know that,
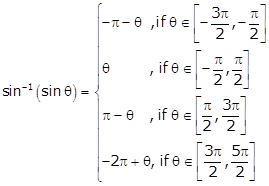
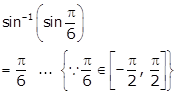
Hence, 
Solution 2(ii)
We know that,
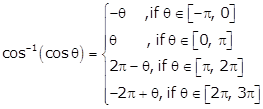
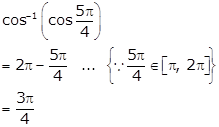
Hence, 
Solution 2(iv)
We know that,
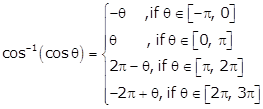
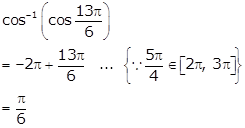
Hence, 
Solution 1(ii)
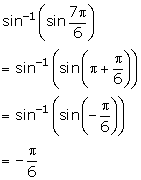
Solution 1(iii)
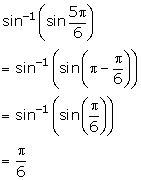
Solution 1(iv)
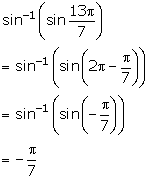
Solution 1(v)
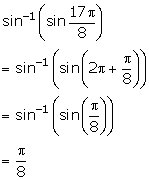
Solution 1(vi)
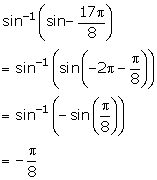
Solution 1(vii)
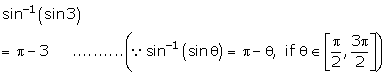
Solution 1(viii)
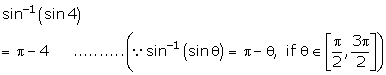
Solution 1(ix)
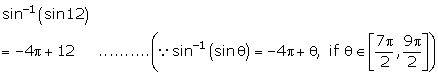
Solution 1(x)
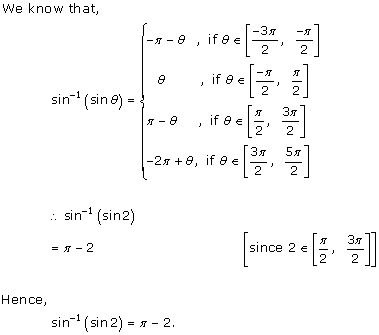
Solution 2(i)
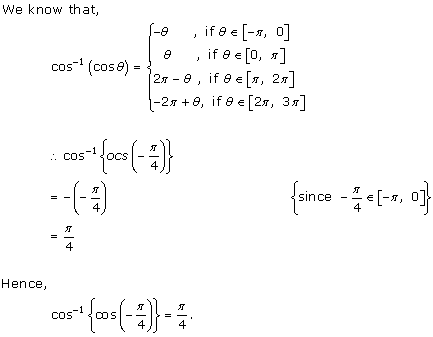
Solution 2(iii)
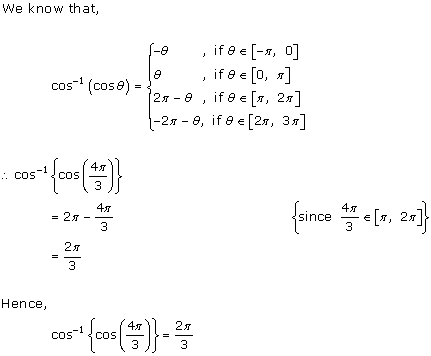
Solution 2(v)
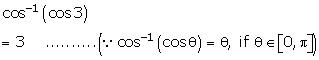
Solution 2(vi)
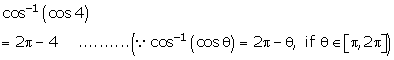
Solution 2(vii)
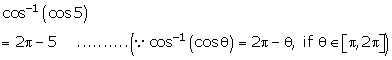
Solution 2(viii)
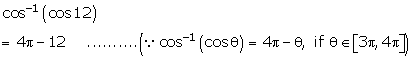
Solution 3(i)
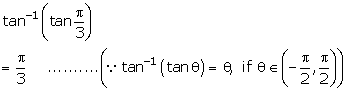
Solution 3(ii)
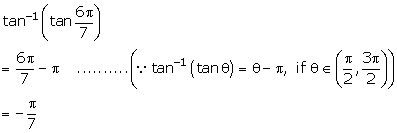
Solution 3(iii)
Solution 3(iv)
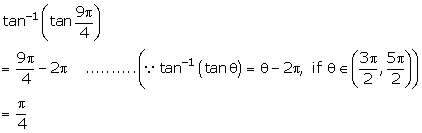
Solution 3(v)
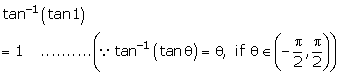
Solution 3(vi)
Solution 3(vii)
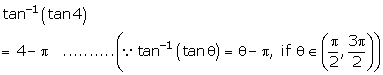
Solution 3(viii)
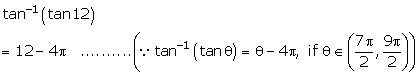
Solution 4(i)
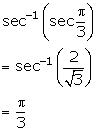
Solution 4(ii)
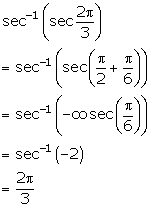
Solution 4(iii)
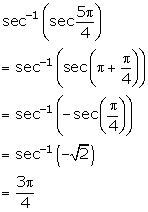
Solution 4(iv)
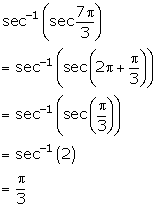
Solution 4(v)
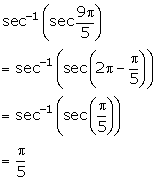
Solution 4(vi)
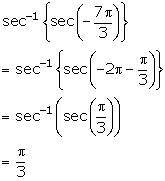
Solution 4(vii)
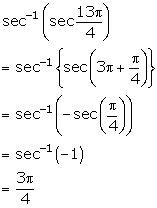
Solution 4(viii)
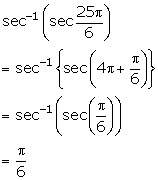
Solution 5(i)
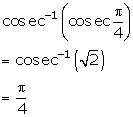
Solution 5(ii)
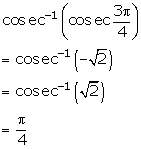
Solution 5(iii)
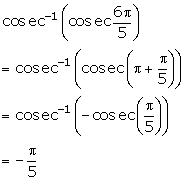
Solution 5(iv)
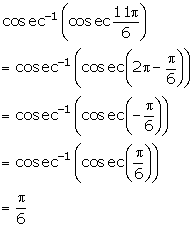
Solution 5(v)
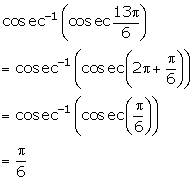
Solution 5(vi)
Solution 6(i)
Solution 6(ii)
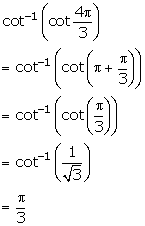
Solution 6(iii)
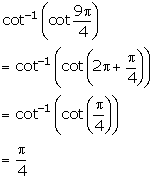
Solution 6(iv)
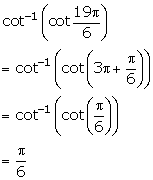
Solution 6(v)
Solution 6(vi)
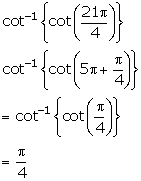
Solution 7(i)
Solution 7(ii)
Solution 7(iii)
Solution 7(iv)
Solution 7(v)
Solution 7(vi)
Solution 7(vii)
Solution 7(viii)
Solution 7(ix)
Solution 7(x)
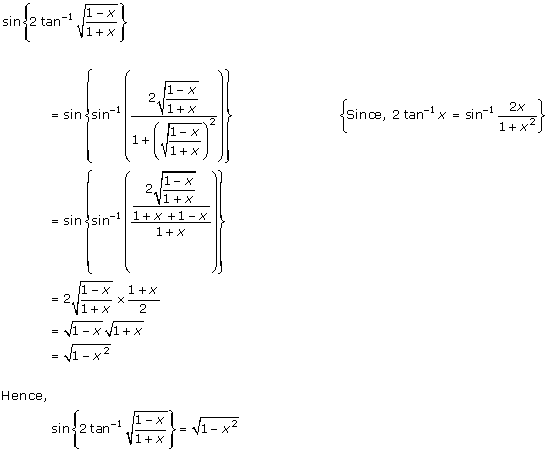
Inverse Trigonometric Functions Exercise Ex. 4.8
Solution 1(i)
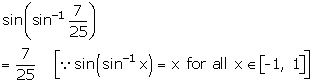
Solution 1(ii)
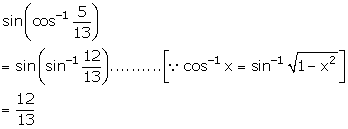
Solution 1(iii)
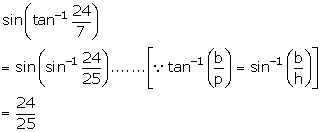
Solution 1(iv)
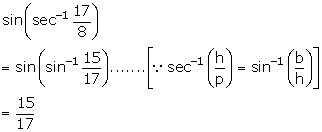
Solution 1(v)
Solution 1(vi)
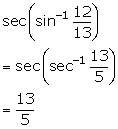
Solution 1(vii)
Solution 1(viii)
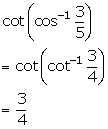
Solution 1(ix)
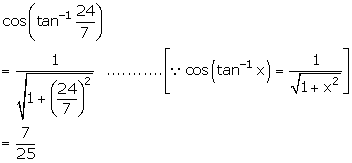
Solution 2(i)
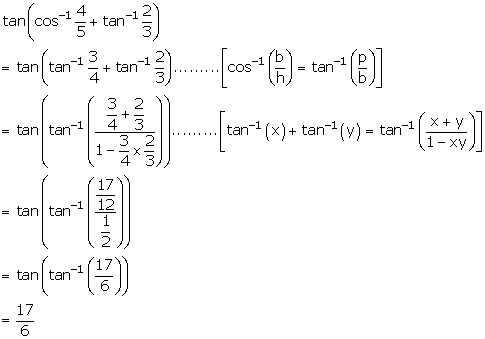
Solution 2(ii)
Solution 2(iii)
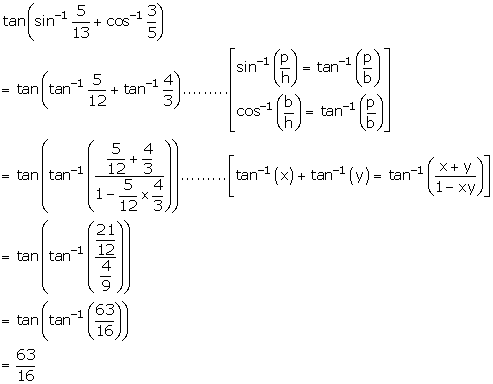
Solution 2(iv)
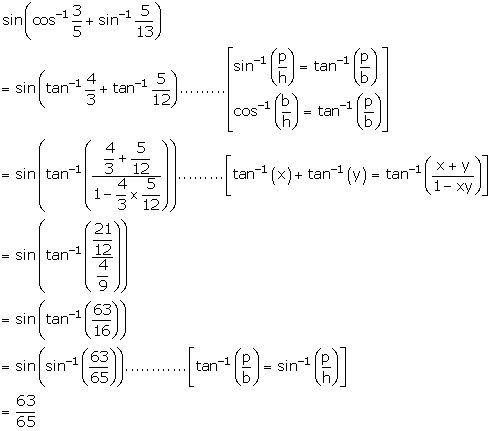
Solution 3
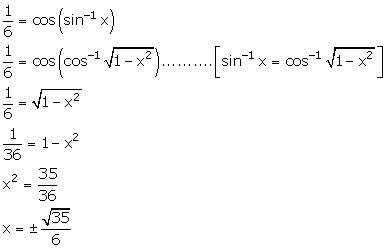
Solution 4
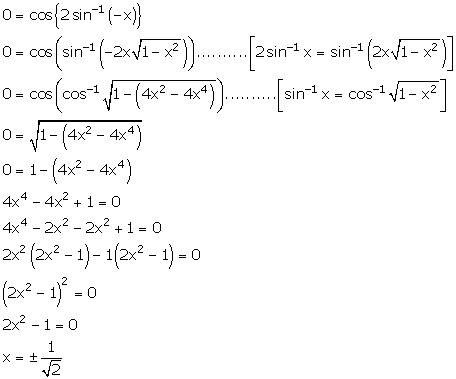
Inverse Trigonometric Functions Exercise Ex. 4.9
Solution 1(iii)
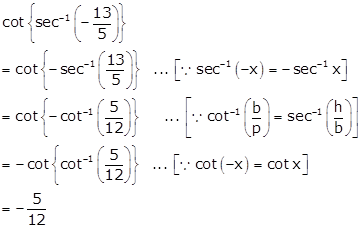
Hence, 
Solution 1(i)
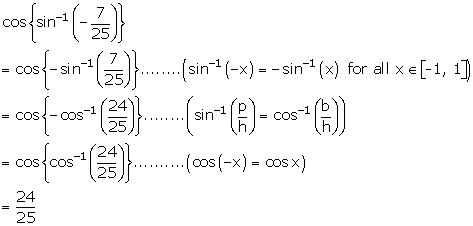
Solution 1(ii)
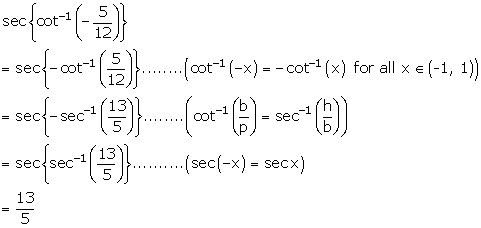
Solution 2(i)
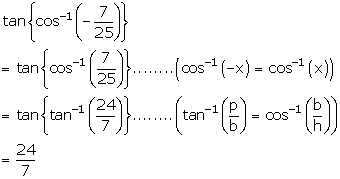
Solution 2(ii)
Solution 2(iii)
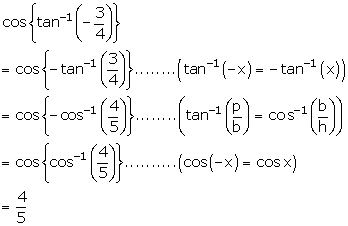
Solution 3
Inverse Trigonometric Functions Exercise Ex. 4.10
Solution 1(i)
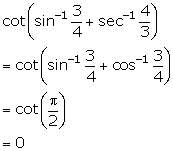
Solution 1(ii)
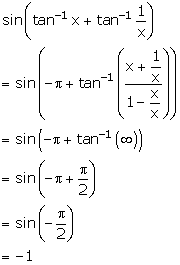
Solution 1(iii)
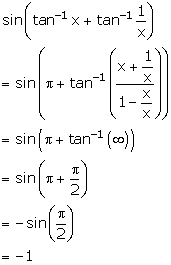
Solution 1(iv)
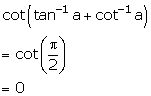
Solution 1(v)
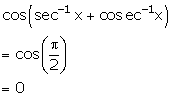
Solution 2
[ ∏/2 - sin-1 x ] + [ ∏/2 - sin-1y ] = ∏/4
sin-1x + sin-1y = ∏ - ∏/4
sin-1x + sin-1y = 3∏/4
Solution 3
On adding both the equation
Π/2 + sin-1y - cos-1y = Π/2
[ Π/2- cos-1y ] - cos-1y = 0
cos-1y = Π/4
y = 1/√2
on putting y=1/√2 in 2nd equation
cos-1x - Π/4 = Π/6
cos-1x = Π/4 + Π/6
x = cos(Π/4 + Π/6)
x = cos(Π/4)cos(Π/6)-sin(Π/4)sin(Π/6)
x = (√3-1)/2√2
Solution 4
cot(z) = 0 means z = Π/2, 3Π/2, 5Π/2 ………..
cos-1(3/5) + sin-1x = nΠ + Π/2
sin-1x = nΠ + Π/2 - cos-1(3/5)
sin-1x = nΠ + sin-1(3/5)
x = sin(nΠ + sin-1(3/5)) = (-1)n sin (sin-1(3/5))
x = (-1)n 3/5
Solution 5
[ Π/2 - cos-1x ]2 + (cos-1x)2 =17Π2/36
Π2/4 - Πcos-1x + 2(cos-1x)2 =17Π2/36
Let, cos-1x=u
2u2 - Πu + Π2/4 - 17Π2/36 = 0
2u2 - Πu - 2Π2/9 = 0
18u2 - 9Πu -2Π2 = 0
On factorizing
18u2 - 12Πu + 3Πu -2Π2 = 0
6u( 3u -2Π ) + Π( 3u -2Π ) = 0
( 3u -2Π )(6u + Π) = 0
u = -Π/6, 2Π/3
i.e. cos-1x = -Π/6, 2Π/3
but range of cos-1x is [0, π]
x = cos(Π/2 + Π/6)
x = -1/2
Solution 6
sin-1(1/5) + [ Π/2 - sin-1x ] = sin-11
sin-1(1/5) + Π/2 - sin-1x = Π/2
sin-1(1/5) - sin-1x = 0
x = 1/5
Solution 7
Π/2 - cos-1x = Π/6 + cos-1x
Π/3 = 2cos-1x
cos-1x = Π/6
x = √3/2
Solution 8
4sin-1x+cos-1x=Π
3sin-1x+sin-1x+cos-1x=Π
3sin-1x=Π/2 [sin-1x+cos-1x=Π/2]
sin-1x=Π/6
x = sinΠ/6=0.5
Solution 9
tan-1x+cot-1x=Π/2 so the above equation reduces to
cot-1x =2Π/3-Π/2 =Π/6
x= cotΠ/6 =√3
Solution 10
Given: 
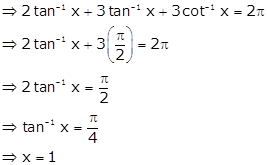
Hence,
Inverse Trigonometric Functions Exercise Ex. 4.11
Solution 1(i)
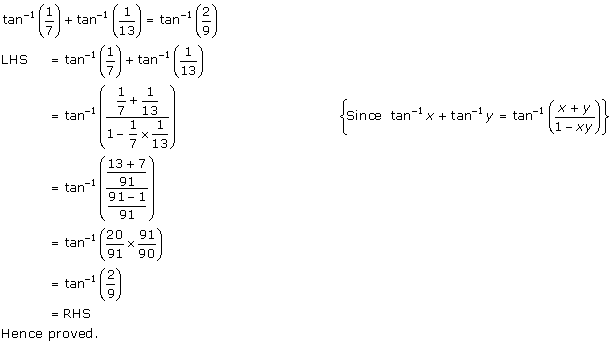
Solution 1(ii)
Solution 1(iii)
Solution 2
Solution 3(i)
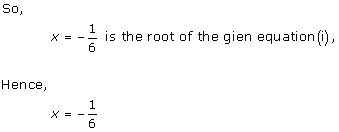
Solution 3(ii)
Solution 3(iii)
Solution 3(iv)
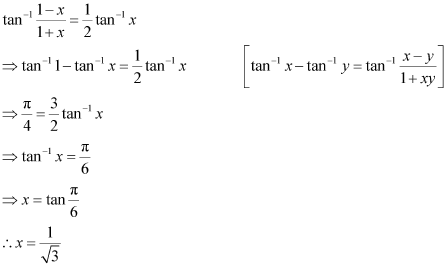
Solution 3(v)
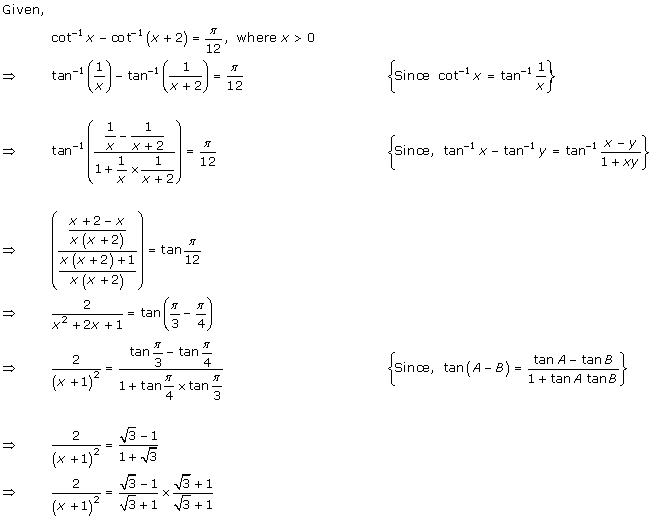
Solution 3(vi)
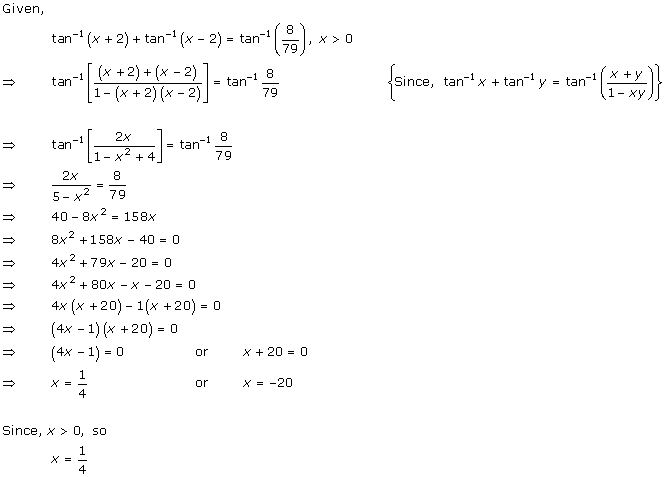
Solution 3(vii)
Solution 3(viii)
Solution 3(ix)
Solution 3(x)
Given: 
As 
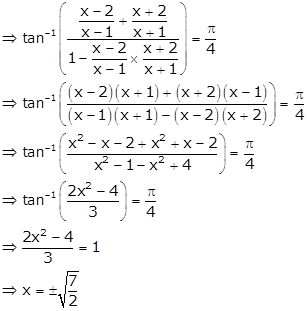
Solution 3(xi)
Given: 
As
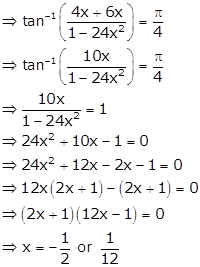
But 
does not satisfy the given equation.
Therefore, 
Solution 4
Inverse Trigonometric Functions Exercise Ex. 4.12
Solution 1
Solution 2(i)
Solution 2(ii)
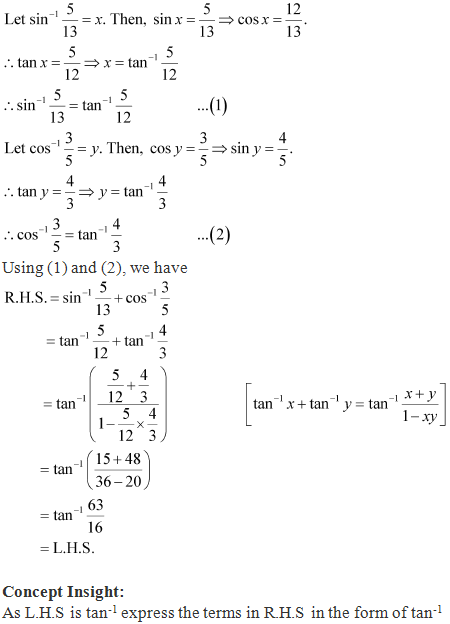
Solution 2(iii)
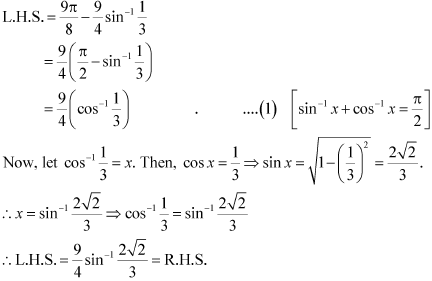
Solution 3(i)
Solution 3(ii)
Solution 3(iii)
Given: 
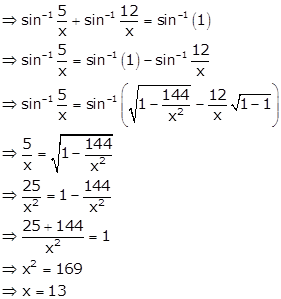
Inverse Trigonometric Functions Exercise Ex. 4.13
Solution 1
Solution 2
Solution 3
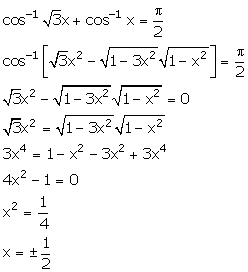
Solution 4
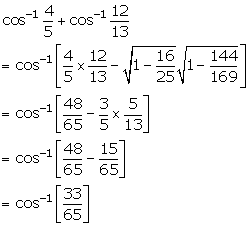
Solution 5
Let 
Let 
We know that, sin(x + y) = sinx cosy + cosx siny
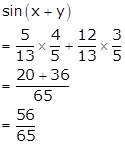
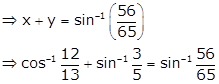
Inverse Trigonometric Functions Exercise Ex. 4.14
Solution 1(i)
Solution 1(ii)
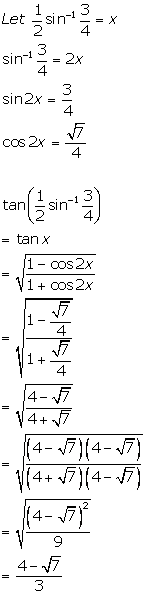
Solution 1(iii)
Solution 1(iv)
Solution 2(i)
Solution 2(ii)
Solution 2(iii)
Solution 2(iv)
Solution 2(v)
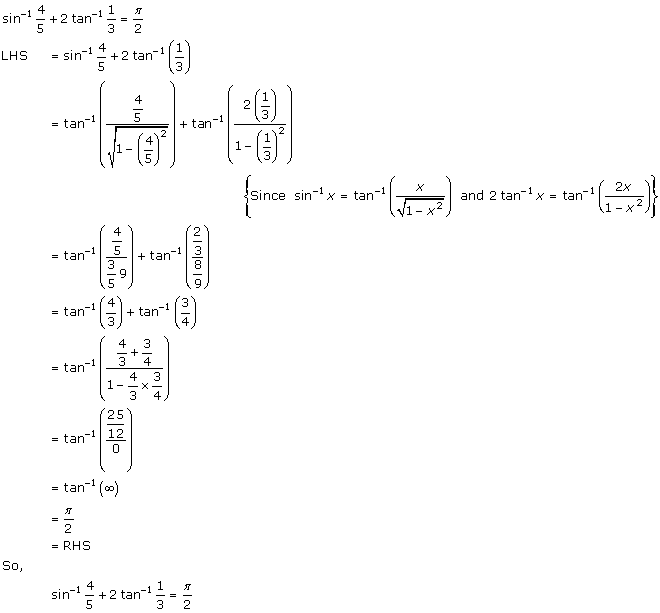
Solution 2(vi)
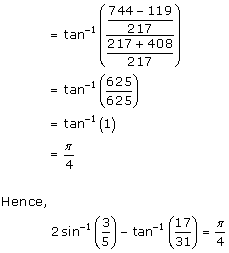
Solution 2(vii)
Solution 2(viii)
Solution 2(ix)
Solution 2(x)
Solution 3
Solution 4(i)
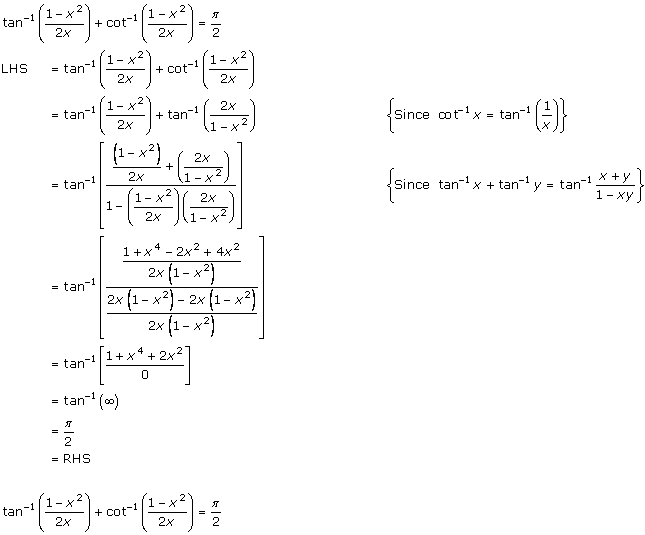
Solution 4(ii)
Solution 4(iii)
Let 
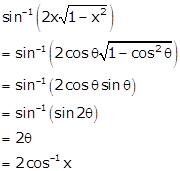
Hence, 
Solution 5
Solution 6
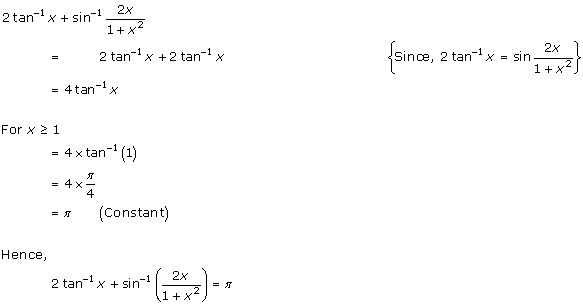
Solution 7(i)
Solution 7(ii)
Solution 8(i)
Solution 8(ii)
Solution 8(iii)
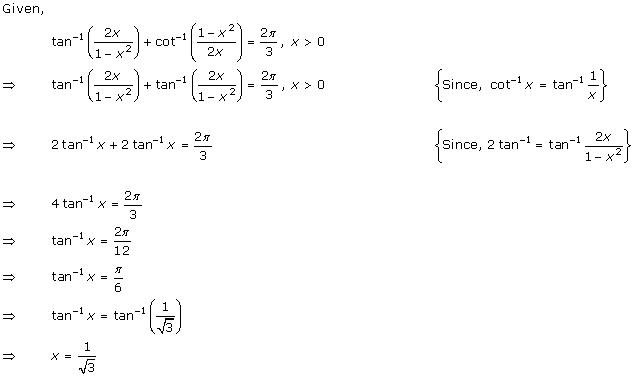
Solution 8(iv)
Thus, the solution is 
Solution 8(v)
Given: 
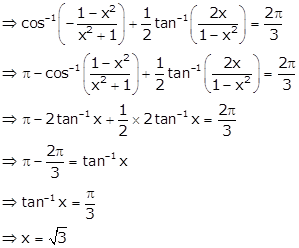
Solution 8(vi)
Given: 
Using the formula
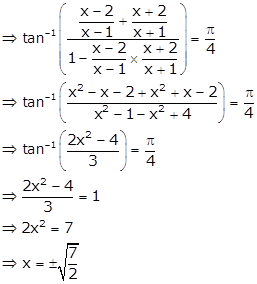
Solution 9
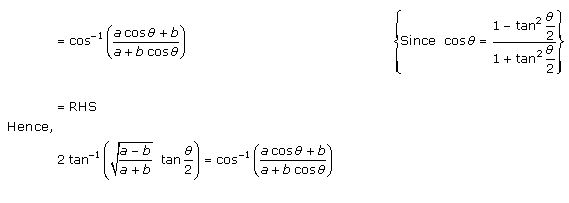
Solution 10
Solution 11
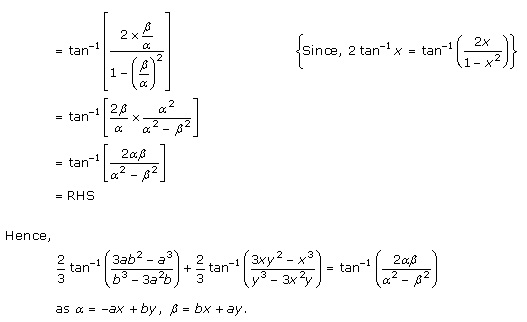
Inverse Trigonometric Functions Exercise MCQ
Solution 1
Correct option: (a)
Solution 2
Correct option: (d)
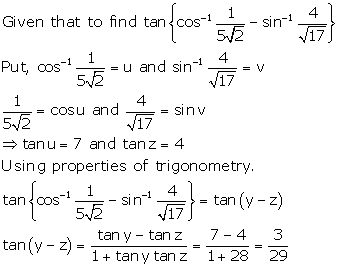
Solution 3
Correct option: (c)
Solution 4
Correct option: (a)
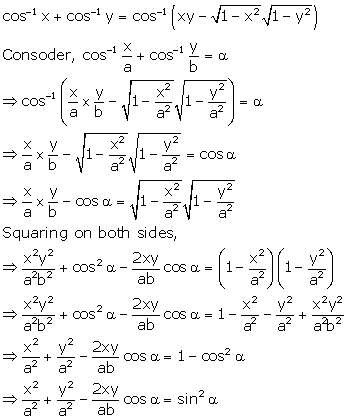
Solution 5
Correct option: (a)
Solution 6
Correct option: (b)
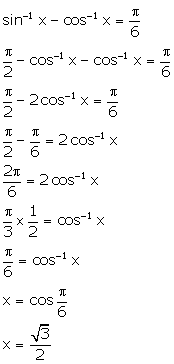
Solution 7
Correct option: (a)
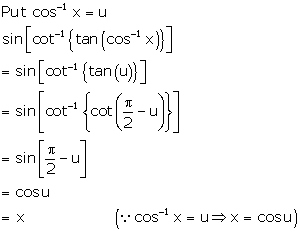
Solution 8
Correct option: (a)
Solution 9
Correct option: (a)
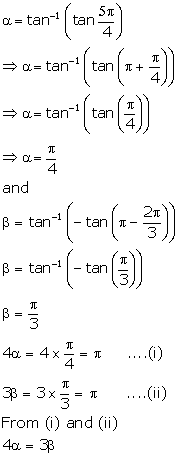
Solution 10
Correct option: (c)
Solution 11
Correct option: (b)
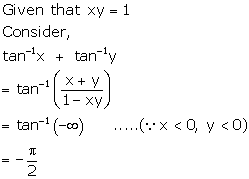
Solution 12
Correct option: (a)
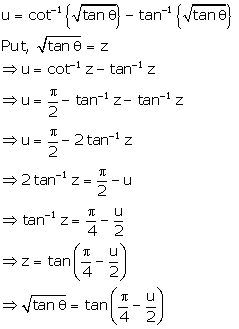
Solution 13
Correct option: (c)
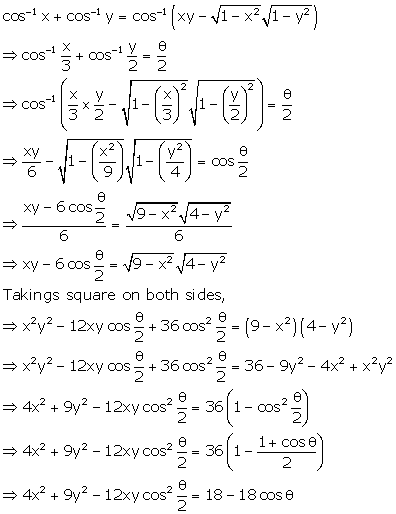
Solution 14
Correct option: (a)
Solution 15
Correct option: (b)
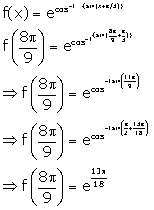
Solution 16
Correct option: (d)
Solution 17
Correct option: (c)
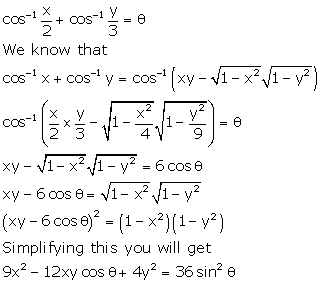
Solution 18
Correct option: (b)
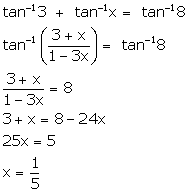
Solution 19
Correct option: (b)
Solution 20
Correct option: (d)
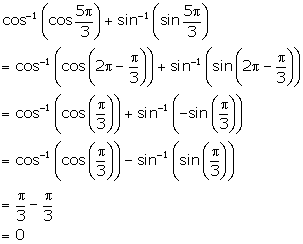
Solution 21
Correct option: (d)
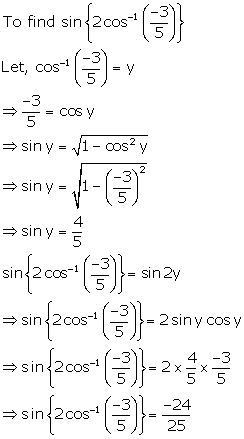
Solution 22
Correct option: (a)
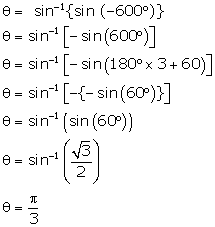
Solution 23
Correct option: (a)
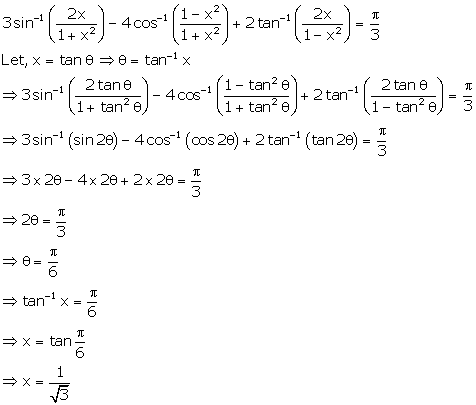
Solution 24
Correct option: (c)
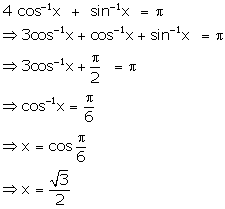
Solution 25
Correct option: (d)
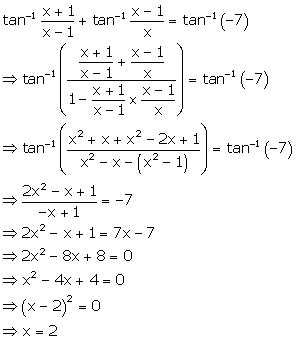
Solution 26
Correct option: (a)
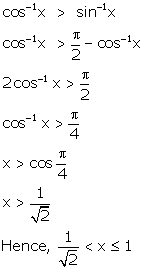
Solution 27
Correct option: (b)
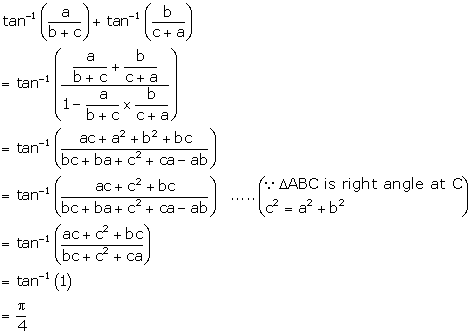
Solution 28
Correct option: (c)
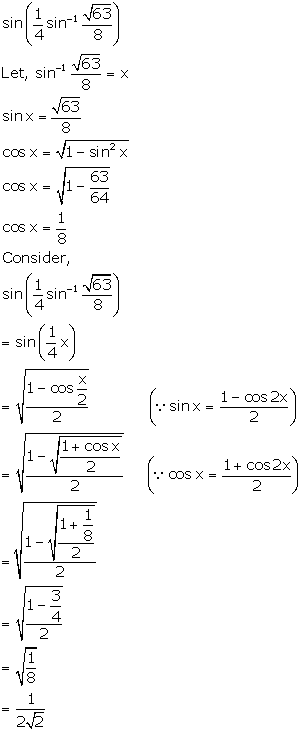
Solution 29
Correct option:(a)
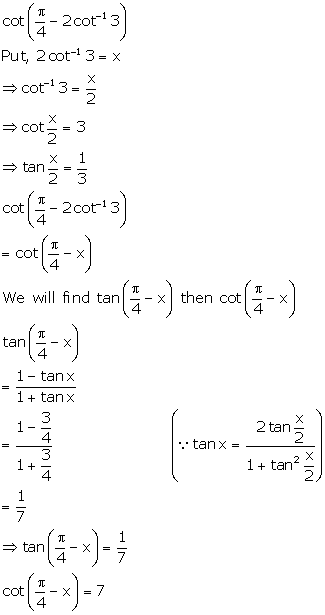
Solution 30
Correct option: (c)
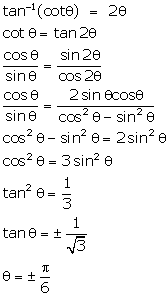
Solution 31
Correct option: (d)
Solution 32
Correct option: (c)
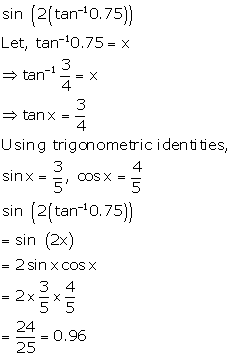
Solution 33
Correct option: (a)
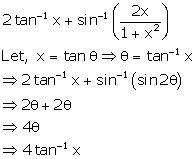
Solution 34
Correct option: (c)
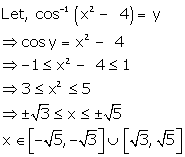
Solution 35
Correct option: (a)
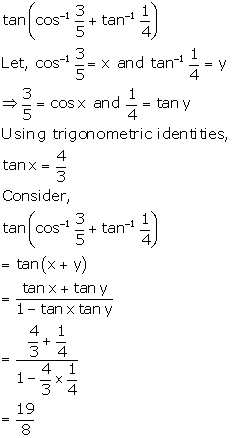
Solution 36
Given: 
… (i)
We know that 
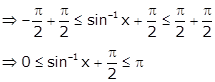
As we know that 
Comparing the above inequality with (i), we get
Solution 37
Let 
We know that, 
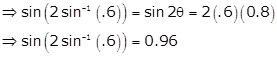
Solution 38
Let 
We know that, 
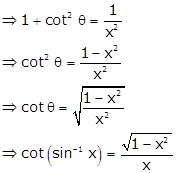
Solution 39
Given: 
We know that 
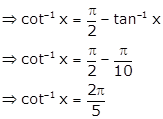
Solution 40
One
branch of cos-1 other than the principal
value branch corresponds to 
.
Solution 41
The
principal value branch of sec-1is 
.
Solution 42
The
principal value branch of tan-1is 
.
Solution 43
The
principal value branch of cosec-1is 
.
Solution 44
Let
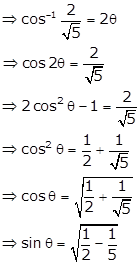
We
know that 
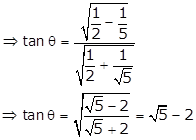
Solution 45
Given: 3tan-1x + cot-1x = π
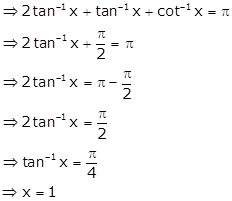
Solution 46
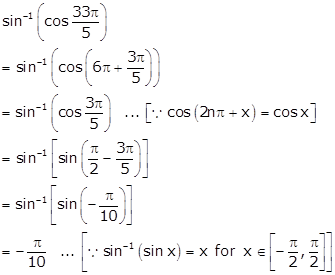
Hence,
Solution 47
We know that,
when xy < 1
Therefore,
is valid when
Hence,
the given expression is valid for 
Solution 48
We know that,
, which is the principal value branch of tan-1x
Now,
As
Inverse Trigonometric Functions Exercise Ex. 4VSAQ
Solution 1
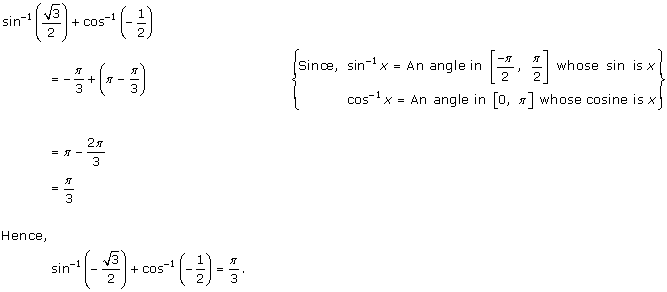
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
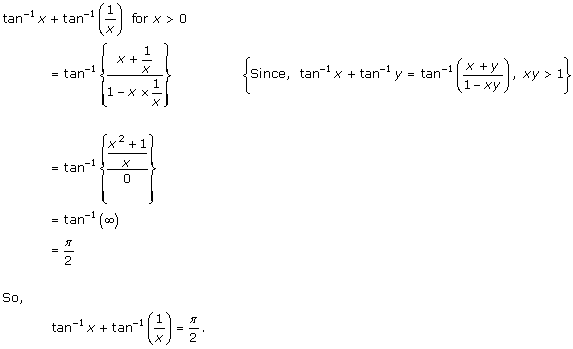
Solution 7
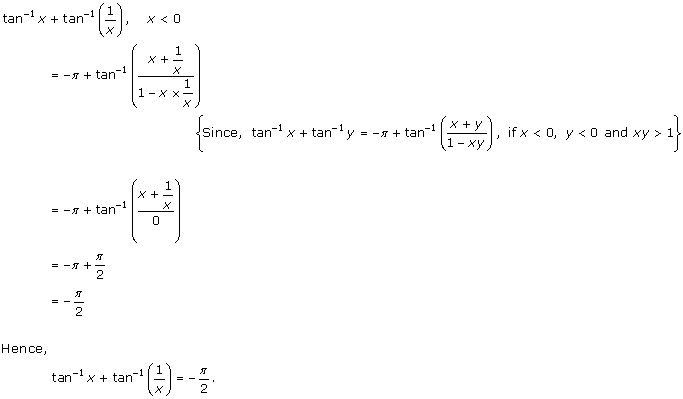
Solution 8
Solution 9
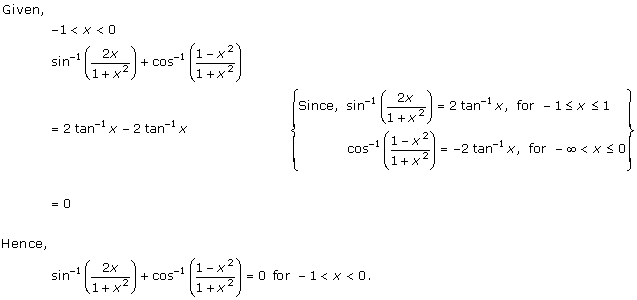
Solution 10
Solution 11
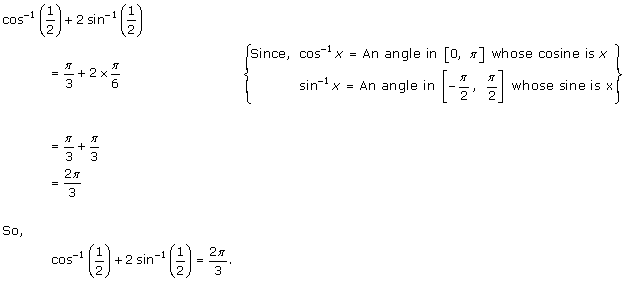
Solution 12
Solution 13
Solution 14
Solution 15
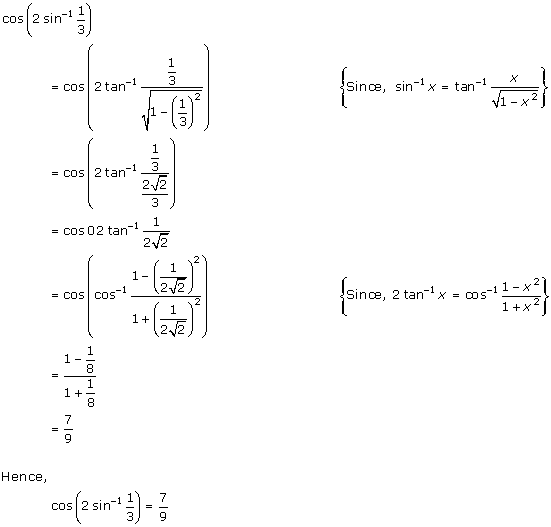
Solution 16
Solution 17
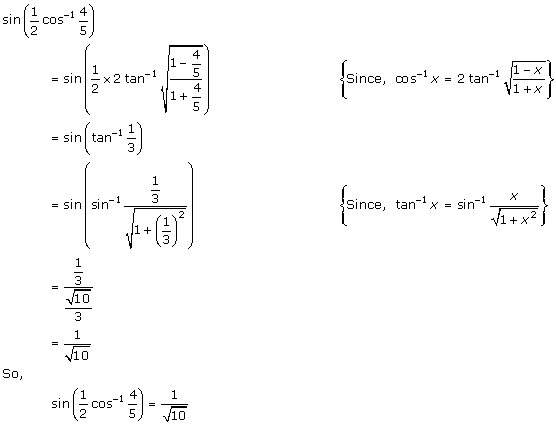
Solution 18
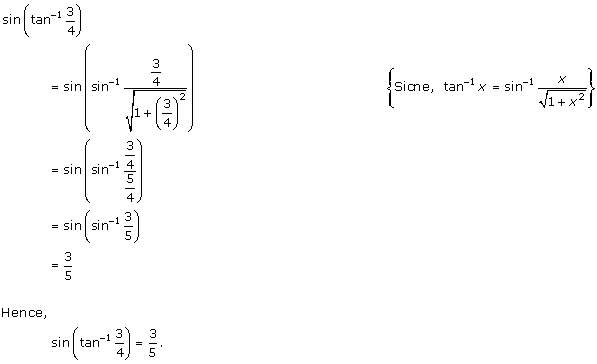
Solution 19
Solution 20
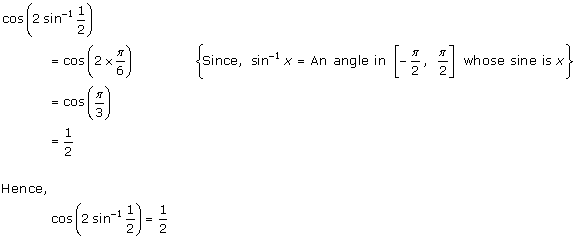
Solution 21
Solution 22
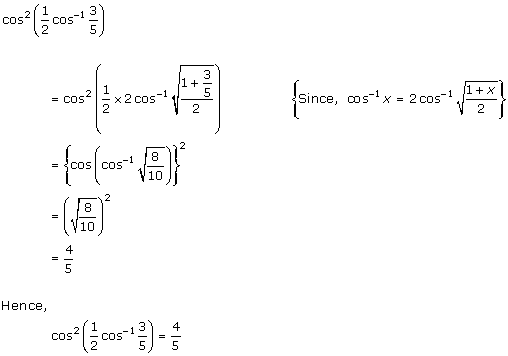
Solution 23
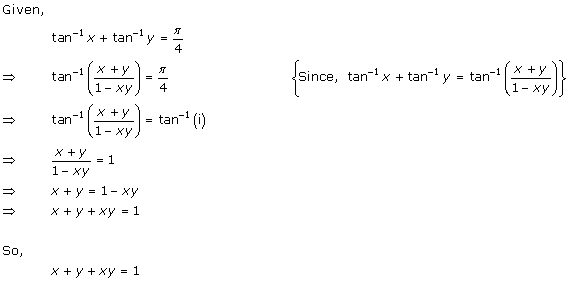
Solution 24
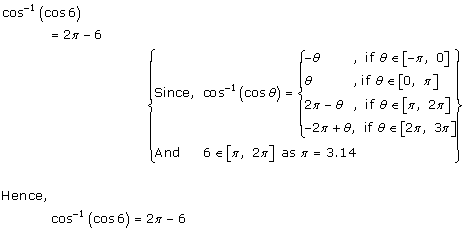
Solution 25
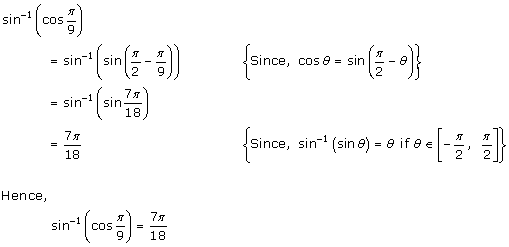
Solution 26
Solution 27
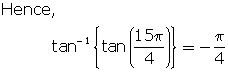
Solution 28
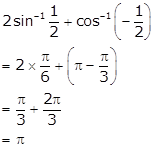
Hence,
Solution 29
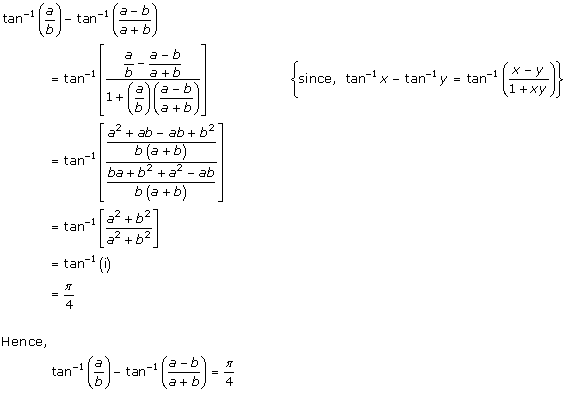
Solution 30
Solution 31
Solution 32
Solution 33
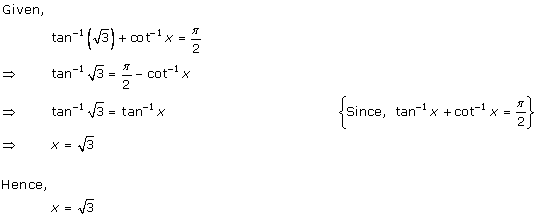
Solution 34
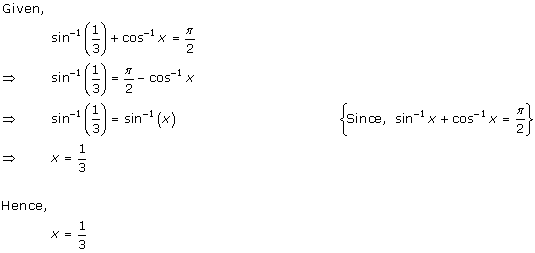
Solution 35
Solution 36
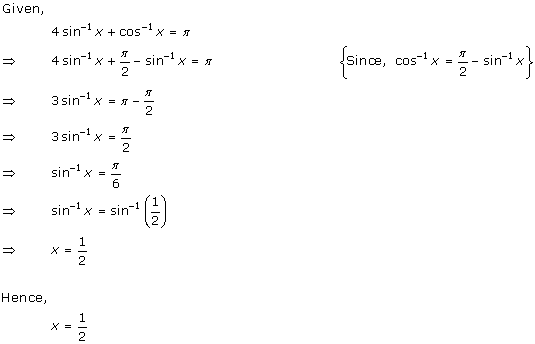
Solution 37
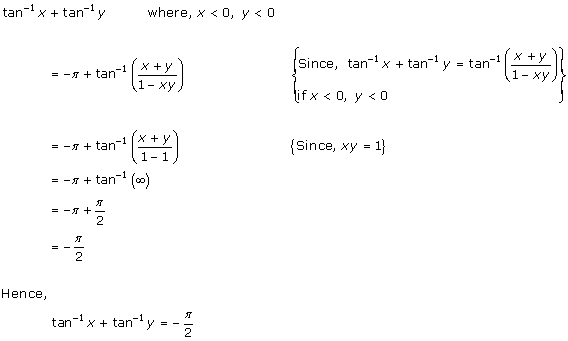
Solution 38
Solution 39
Let
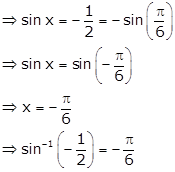
Solution 40
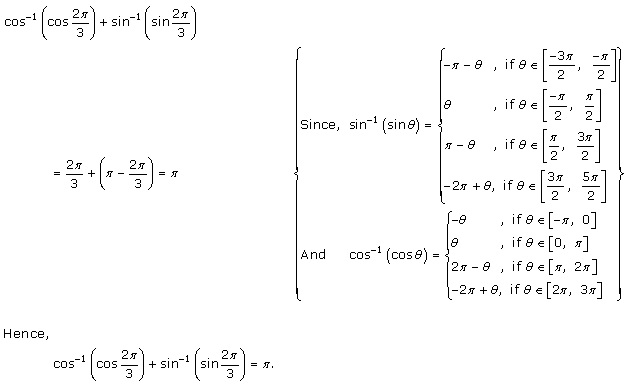
Solution 41
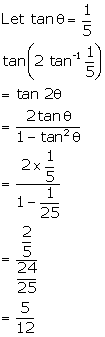
Solution 42
Solution 43
Solution 44
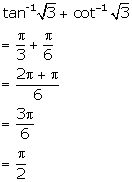
Solution 45
Solution 46
We know that,
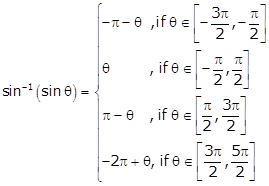
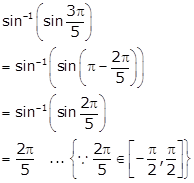
Hence,
Solution 47
Let
The
range of 
is R - (-1,
1).
So,
does not
belong to this range.
Thus,
is undefined.
Hence,
Solution 48
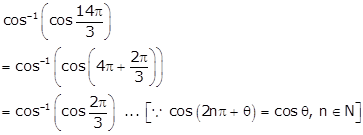
Hence,
Solution 49
Using
the property that, when 
we have
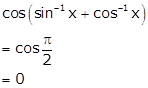
Solution 50
We
know that when
As
we have
Solution 51
Hence,
Solution 52
Let
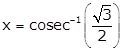
Now, range of cosec x is R - (-1, 1)
As
does not
belong to this range, so cosec x also does not belong to this range.
Thus, the value of x will be undefined.
Hence,
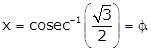
Solution 53
For x < 0,
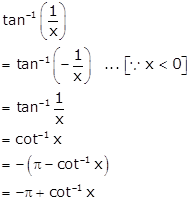
Hence,
Solution 54
for all 
Solution 55
We
know that,
Solution 56
Given:
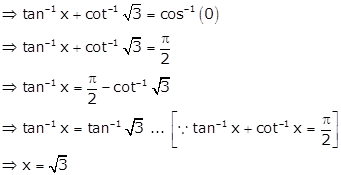
Solution 57
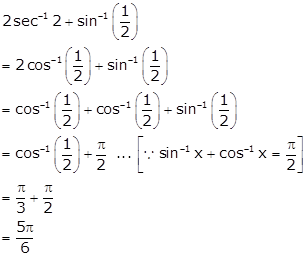
Hence,
Solution 58
Given:
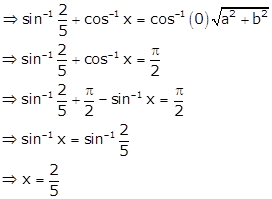
Hence,
the value of x is 
Solution 59
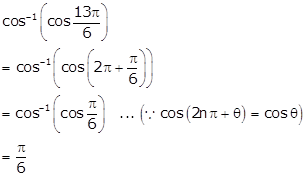
Hence,
Solution 60
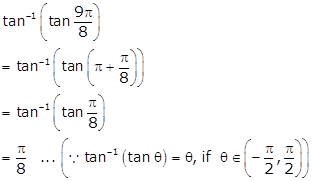
Hence,
Solution 61
As
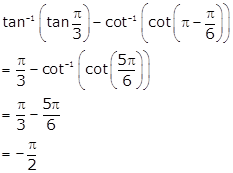
Hence,
Solution 62
As
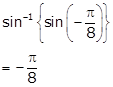
Hence,
Solution 63
Let
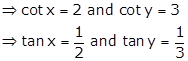
Now,
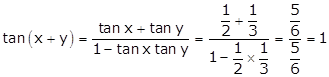
Let
be the third
angle.
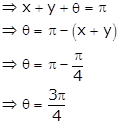
Hence,
the third angle is 