Class 12-commerce RD SHARMA Solutions Maths Chapter 2: Functions
Functions Exercise MCQ
Solution 55
Given: ![]() be defined by
be defined by
![]()
For inverse, we first need to check whether f is invertible.
Let ![]() such that
f(x) = f(y)
such that
f(x) = f(y)
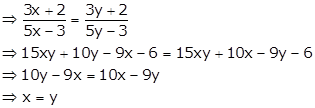
So, f is one-one.
Let y = f(x)
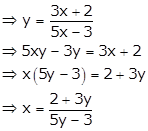
Therefore, for
every ![]() there exist y
∈ R such that
f(x) = y.
there exist y
∈ R such that
f(x) = y.
Thus, f is bijective and so invertible.
Taking y = f(x), we get
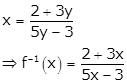
Hence, ![]()
Solution 56
Given: f: R → R be defined
by ![]()
As x ∈ R, so it can take the value 0 as well.
At x = 0, f(x) is not defined.
Thus, f is not defined.
Solution 57
f: R → R is given by f(x) = 3x2 - 5
g: R → R is given by ![]()
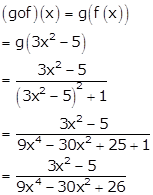
Solution 58
a. If we take f: Z → Z defined by f(x) = x2
Clearly, it is not one-one as considering f(x) = f(y) will give us
x = ±y
Therefore, it is not a bijection.
b. Consider f: Z → Z defined by f(x) = x + 2
Let x, y ∈ Z such that f(x) = f(y)
∴ x + 2 = y + 2
∴ x = y
So, f is one-one.
For x in the domain Z, f(x) will also take integer values.
So, the range of f is Z.
Therefore, f is onto.
Thus, f is a bijection.
c. Consider f: Z → Z defined by f(x) = x + 2
Let x, y ∈ Z such that f(x) = f(y)
∴ x = y
So, f is one-one.
For x in the domain Z, f(x) = 2x + 1 will take odd integer values.
So, the range of f is not same as its co-domain.
Therefore, f is not onto.
Thus, f is not a bijection.
d. If we take f: Z → Z defined by f(x) = x2 + 1
Clearly, it is not one-one as considering f(x) = f(y) will give us
x = ± y
Therefore, it is not a bijection.
Hence, option (b) is correct.
Solution 59
It is given that f: A → B and g: B → C are two bijective functions.
Consider,

Thus, ![]()
Solution 60
It is given that
f: N → R as ![]() and g: Q → R as g(x) = x
+ 2.
and g: Q → R as g(x) = x
+ 2.
Now,
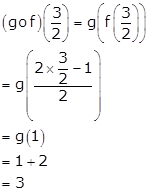
Hence, ![]()
Solution 1
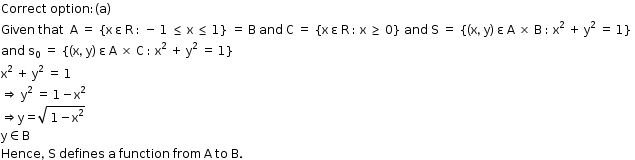
Solution 2
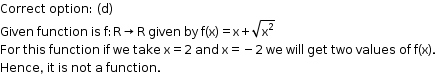
Solution 3

Solution 4

Solution 5

Solution 6
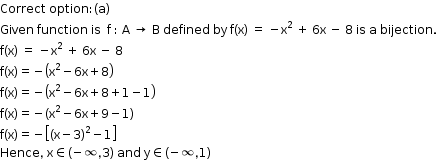
Solution 7

Solution 8
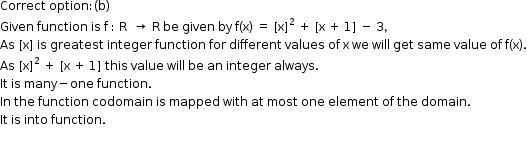
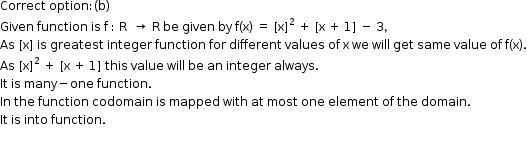
Solution 9

Solution 10

Solution 11

Solution 12

Solution 13

Solution 14

Solution 15
![]()
![]()

Solution 16

Solution 17
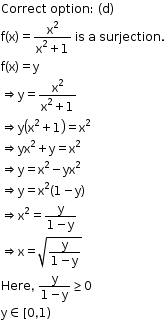
Solution 18
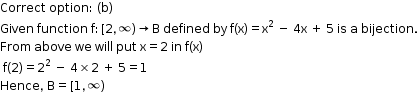
Solution 19

Solution 20
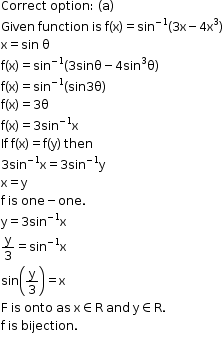
Solution 21
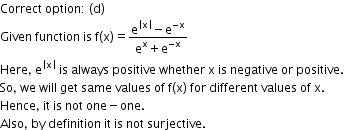
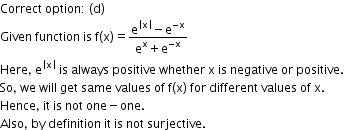
Solution 22

Solution 23

Solution 24

Solution 25

Solution 26

Solution 27
![]()
Solution 28

Solution 29

Solution 30

Solution 31

Solution 32
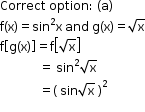
Solution 33

Solution 34

Solution 35
 ANSWER PENDING
ANSWER PENDING
Solution 36

Solution 37
 ANSWER PENDING
ANSWER PENDING
Solution 38
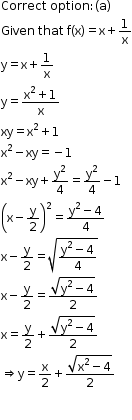
Solution 39

Solution 40

Solution 41

Solution 42
 ANSWER PENDING
ANSWER PENDING
Solution 43

Solution 44
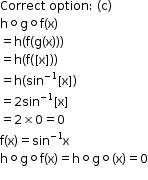
Solution 45

Solution 46

Solution 47

Solution 48

Solution 49

Solution 50
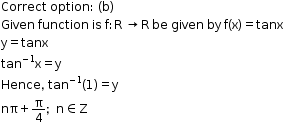
Solution 51

Solution 52

Solution 53
![]()

Solution 54
![]()
Functions Exercise Ex. 2.1
Solution 1(i)

Solution 1(ii)

Solution 1(iii)

Solution 2
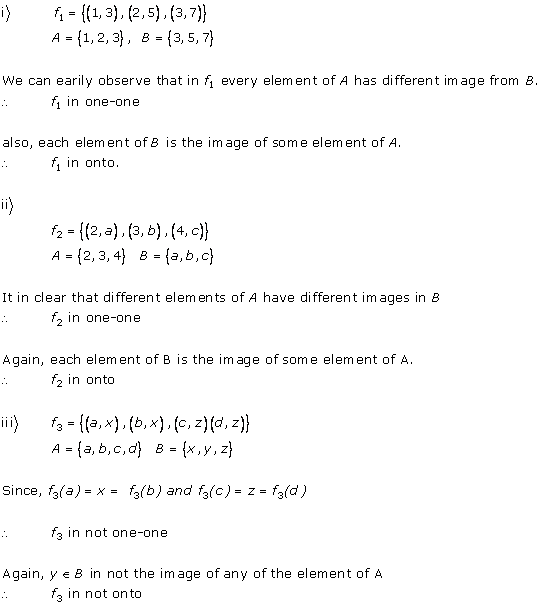
Solution 3

Solution 4

Solution 5(i)

Solution 5(ii)
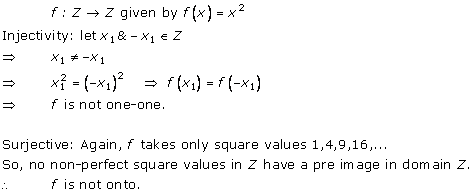
Solution 5(iii)

Solution 5(iv)

Solution 5(v)

Solution 5(vi)

Solution 5(vii)

Solution 5(viii)

Solution 5(ix)
Solution 5(x)

Solution 5(xi)

Solution 5(xii)

Solution 5(xiii)

Solution 5(xiv)

Solution 5(xv)

Solution 5(xvi)
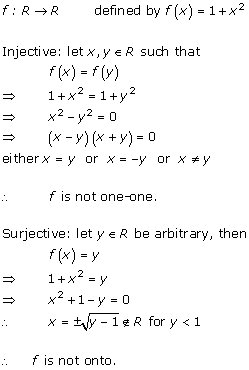
Solution 6

Solution 7
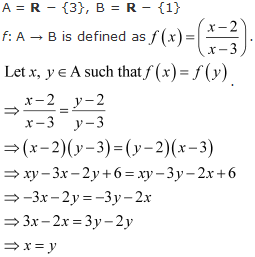

Solution 10

Solution 11
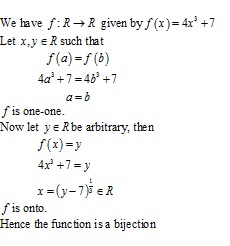
Solution 12
We have f : R → R given by f(x) = ex
let x, y ∊ R, such that
f(x) = f(y)
⇒ ex = ey
⇒ ex-y = 1 = e°
⇒ x - y = 0
⇒ x = y
∴ f is one-one
clearly range of f = (0, ∞) ≠ R
∴ f is not onto
when co-domain is replaced by 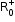 i.e, (0, ∞) then f becomes an onto function.
i.e, (0, ∞) then f becomes an onto function.
Solution 13

Solution 14
Since f is one-one, three elements of {1, 2, 3} must be taken to 3 different elements of the co-domain {1, 2, 3} under f.
Hence, f has to be onto.
Solution 15
Suppose f is not one-one.
Then, there exists two elements, say 1 and 2 in the domain whose image in the co-domain is same.
Also, the image of 3 under f can be only one element.
Therefore, the range set can have at most two elements of the co-domain {1, 2, 3}
i.e f is not an onto function, a contradiction.
Hence, f must be one-one.
Solution 16

Solution 17
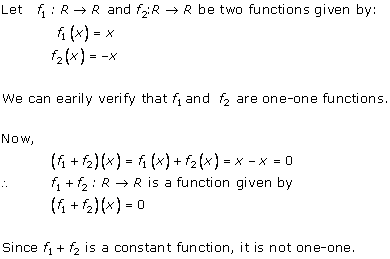
Solution 18
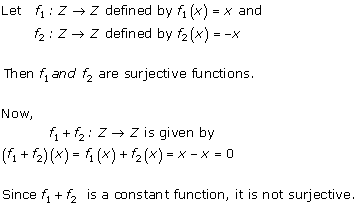
Solution 19

Solution 20
Solution 22
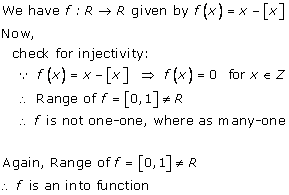
Solution 23

Solution 5(xvii)
Given: f: R → R, defined by ![]()
Injective: Let x, y ∈ R such that f(x) = f(y)

This does not imply x = y
Therefore, f is not one-one.
Surjective: Let y ∈ R be arbitrary, then
f(x) = y
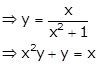
This does not give any value for x.
Therefore, f is not onto.
Thus, it is not bijective.
Solution 8(i)
Given: f: A → A, defined by ![]()
Injective: Let x, y ∈ A such that f(x) = f(y)
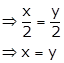
Therefore, f is one-one.
Surjective: For f(x), x ∈ [-1, 1]
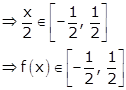
Therefore, range is the subset of codomain.
Thus, f is not onto.
Hence, f is one-one but not onto.
Solution 8(ii)
Given: g: A → A, defined by ![]()
Injective: Let x, y ∈ A such that g(x) = g(y)
![]()
Therefore, f is not one-one.
Surjective: For f(x), x ∈ [-1, 1]
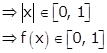
Therefore, range is the subset of codomain.
Thus, f is not onto.
Hence, f is neither one-one nor onto.
Solution 8(iii)
Given: h: A → A, defined by ![]()
Injective: Let x, y ∈ A such that h(x) = h(y)
![]()
Therefore, f is not one-one.
Surjective: For f(x) = x2, x ∈ [-1, 1]
∴ x2∈ [0, 1]
So, the range is subset of co-domain.
Thus, f is not onto.
Hence, f is neither one-one nor onto.
Solution 9(i)
Given set of ordered pair is {(x, y): x is a person, y is the mother of x}
Now biologically, each person 'x' has only one mother.
So, the above set of ordered pairs is a function.
Also, more than one person may have same mother.
So the function is many-one and surjective.
Solution 9(ii)
Given set of ordered pair is {(a, b): 'a' is a person, 'b' is an ancestor of 'a'}
Clearly, a person can have more than one ancestors.
So, the above set of ordered pairs is not a function.
Solution 21
Given: A = {2, 3, 4}, B = {2, 5, 6, 7}
a. Consider f: A → B defined by f(x) = x + 3
Clearly, f is injective because each element of A has distinct output in B.
b. Consider g: A → B defined by g(x) = 3
Here, g is a constant function.
Therefore, each element in A has the same output in B.
Thus, g is not injective.
c. Consider h: A → B such that h = {(2, 2), (3, 5), (4, 7)}
Clearly, h is a mapping from A to B.
Functions Exercise Ex. 2.2
Solution 1(i)

Solution 1(ii)
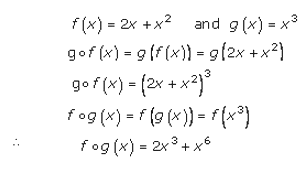
Solution 1(iii)
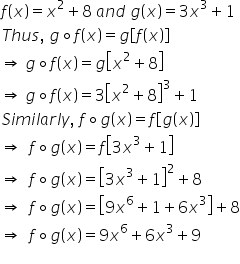
Solution 1(iv)
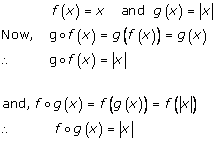
Solution 1(v)

Solution 1(vi)

Solution 2

Solution 3

Solution 4

Solution 5

Solution 6
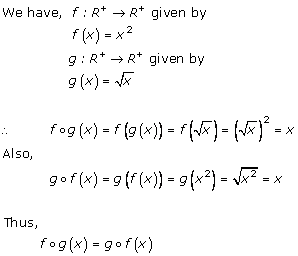
Solution 7
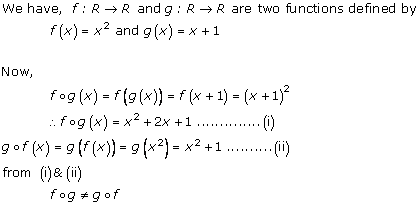
Solution 8

Solution 9
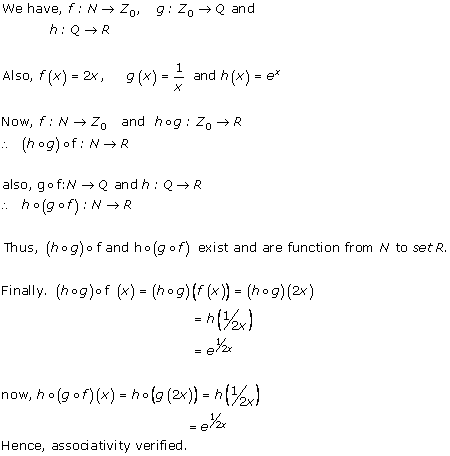
Solution 10
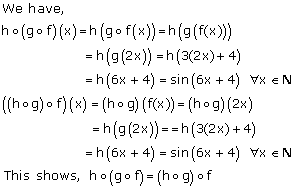
Solution 11


Solution 12
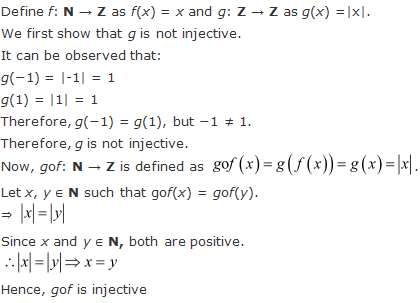
Solution 14

Solution 13
Given: ![]()
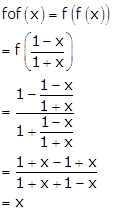
Hence, fof(x) = x.
Functions Exercise Ex. 2VSAQ
Solution 37
We have f: [5, 6] → [2, 3] and g: [2, 3] → [5, 6] are given by:
f = {(5, 2), (6, 3)} and g = {(2, 5), (3, 6)}
Now, (f o g)(2) = f(g(2)) = f(5) = 2
And, (f o g)(3) = f(g(3)) = f(6) = 3
Therefore, fog = {(2, 2), (3, 3)}.
Solution 38
Let x, y ∈ R such that f(x) = f(y)
∴ 4x - 3 = 4y - 3
∴ x = y
So, f is one-one.
For x ∈ R, 4x - 3 ∈ R
Therefore, range and co-domain are same.
So, f is onto.
Thus, f is bijective and so it is invertible.
Let y = f(x)
∴ y = 4x - 3
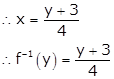
Hence, ![]()
Solution 39
Consider, f = {(1, 3), (2, 3), (3, 2)}
In f, every element in the domain A has unique image.
So, f is a function.
It is given that g = {(1, 2), (1, 3), (3, 1)}
For g, the element 1 in the domain A has two different images.
So, g is not a function.
Solution 40
Given: ![]()
The function f is
defined only when ![]()
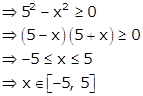
Hence, the domain is [-5, 5].
Solution 41
Given: A = {a, b, c, d} and f: A → A is given by f = {(a, b), (b, d), (c, a), (d, c)}
Here, f-1 will be a function from A to A and given by
f-1 = {(b, a), (d, b), (a, c), (c, d)}
Solution 42
Given: f, g: R → R
Therefore, gof: R → R will be
gof(x) = g(f(x))
= g(2x + 1)
= (2x + 1)2 - 2
= 4x2 + 4x - 1
Hence, gof(x) = 4x2 + 4x - 1.
Solution 43
Given: f: {1, 3, 4} → {1, 2, 5} and g: {1, 2, 5} → {1, 3}
fog(1) = f(g(1)) = f(3) = 5
fog(2) = f(g(2)) = f(3) = 5
fog(5) = f(g(5)) = f(1) = 2
Therefore, fog: {1, 2, 5} → {5, 2}
Hence, fog = {(1, 5), (2, 5), (5, 2)}.
Solution 44
Given: g(x) = αx + β and g = {(1, 1), (2, 3), (3, 5), (4, 7)}
Now, g(1) = 1
∴ α + β = 1 … (i)
And, g(2) = 3
∴ 2α + β = 3 … (ii)
Solving (i) and (ii), we get
α = 2 and β = -1
Solution 45
Given: f(x) = 4 - (x - 7)3
Let y = 4 - (x - 7)3
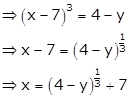
Hence, ![]()
Solution 1
![]()
Solution 2

Solution 3
A = {1, 2, 3} B = {a, b}
The total number of functions is 8
Solution 4

Solution 5

Solution 6
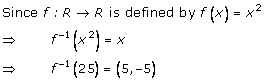
Solution 7
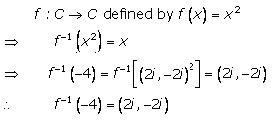
Solution 8
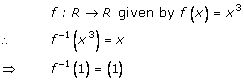
Solution 9

Solution 10
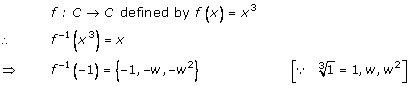
Solution 11
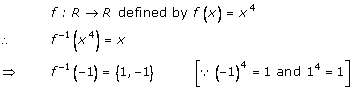
Solution 12

Solution 13
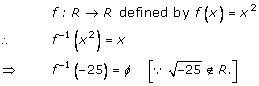
Solution 14

Solution 15
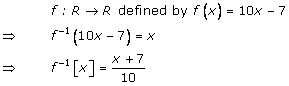
Solution 16

Solution 17

Solution 18
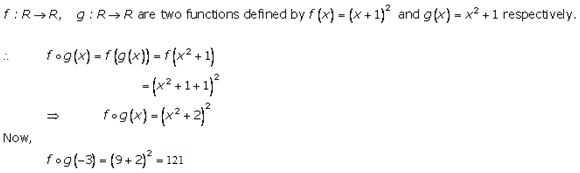
Solution 19
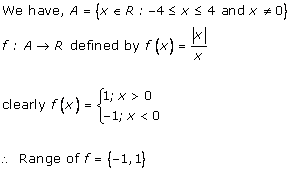
Solution 20

Solution 21

Solution 22

![]()
Solution 23

Solution 24
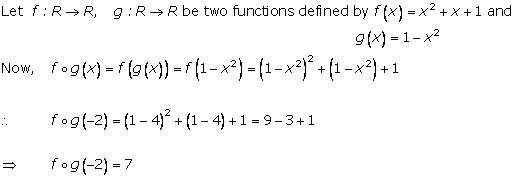
Solution 25
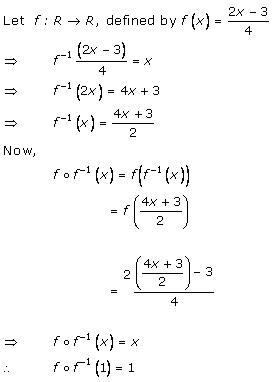
Solution 26

Solution 27

Solution 28

Solution 29

Solution 30

Solution 31

Solution 32

Solution 33

Solution 34

Solution 35
![]()
Solution 36
It is given that
A = {1, 2, 3}, B = {4, 5, 6, 7} and f = {(1,4), (2,5), (3,6)}
The function f is one-one from A to B
Functions Exercise Ex. 2.3
Solution 13
Given: f(x) = |x| + x and g(x) = |x| - x for all x ∈ R
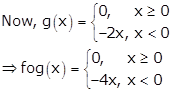
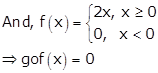
∴ fog(-3) = -4(-3) = 12, fog(5) = 0 and
gof(-2) = 0
Solution 1(i)
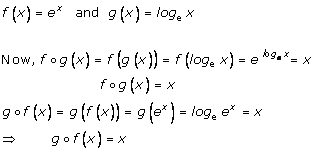
Solution 1(ii)
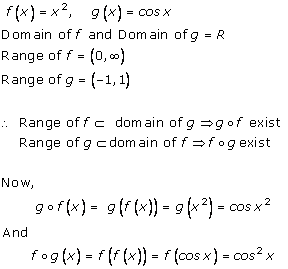
Solution 1(iii)
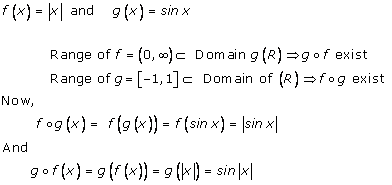
Solution 1(iv)

Solution 1(v)

Solution 1(vi)

Solution 1(vii)
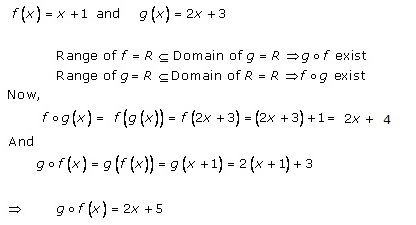
Solution 1(viii)
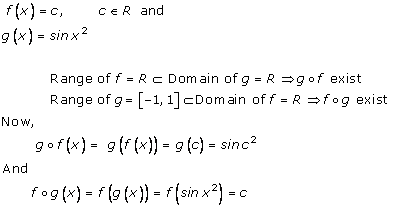
Solution 1(ix)
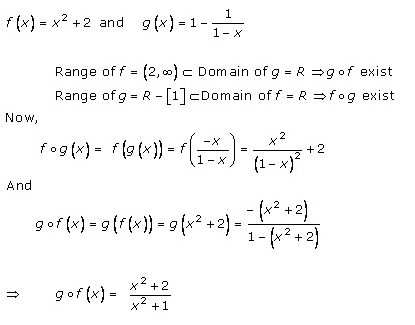
Solution 2

Solution 3

Solution 4
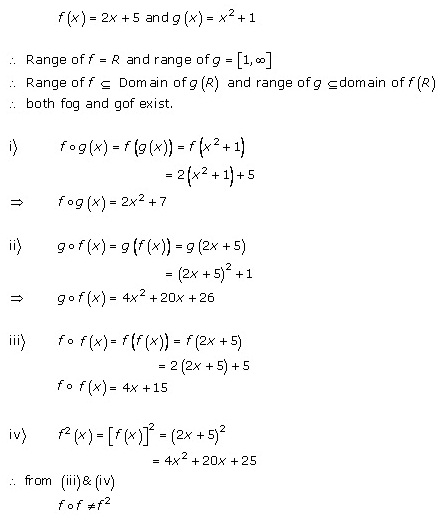
Solution 5

Solution 6

Solution 7
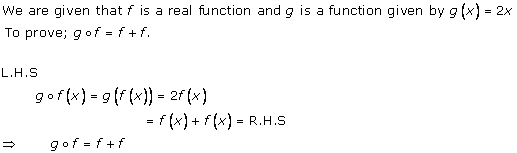
Solution 8

Solution 9
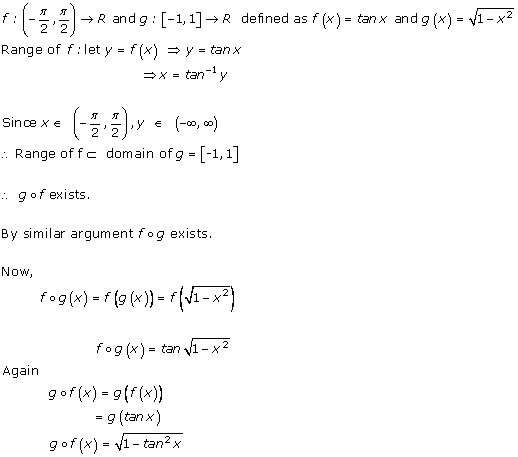
Solution 10

Solution 11(i)

Solution 11(ii)

Solution 11(iii)

Solution 11(iv)

Solution 12

Functions Exercise Ex. 2.4
Solution 15
Given: f(x) = 9x2 + 6x - 5
Let x, y ∈ N such that f(x) = f(y)
∴ 9x2 + 6x - 5 = 9y2 + 6y - 5
∴ 9(x2 - y2) + 6(x - y) = 0
∴ (x - y){9(x + y) + 6} = 0
As x, y ∈ N, 9(x + y) + 6 can't be zero.
∴ x - y = 0
∴ x = y
So, f is one-one.
Clearly, f is onto as range and co-domain are same.
Therefore, f is bijective.
Thus, f is invertible.
Let y = f(x) = 9x2 + 6x - 5
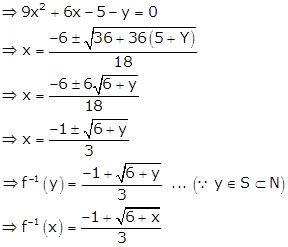
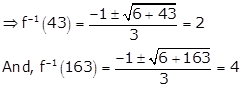
Solution 16
Given: ![]()
Let x, y ∈ ![]() such that
f(x) = f(y)
such that
f(x) = f(y)
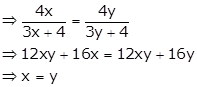
So, f is one-one.
Clearly, f is
onto as the co-domain of ![]() is same as
its range.
is same as
its range.
Therefore, f is bijective.
Thus, f is invertible.
Let y = f(x)
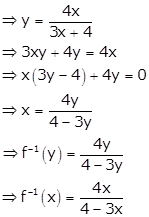
Solution 17
Given: ![]()
Let x, y ∈ A such that f(x) = f(y)
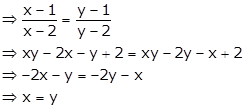
So, f is one-one.
Let y ∈ B

So, for every x ∈ A, there is a y ∈ B such that f(x) = y.
Therefore, f is onto.
Thus, f is bijective and so it is invertible.
Hence, ![]()
Solution 18
Given: f: N → N defined by f(x) = x2 + x + 1
Let x, y ∈ N such that f(x) = f(y)
∴ x2 + x + 1 = y2 + y + 1
∴ x2 - y2 + x - y = 0
∴ (x - y)(x + y + 1) = 0
As x, y ∈ N, so (x2 + x + 1) can't be zero.
∴ x - y = 0
∴ x = y
So, f is one-one.
Since x ∈ N, x2 + x + 1 > 3 as the minimum value x can take is 1.
Therefore, range of f = (3, ∞)
As the co-domain and range does not match, f is not onto.
But, f: N → (3, ∞) is onto as the range matches with co-domain.
Thus, f: N → S is a bijective function and so it is invertible.
Let y = f(x)
∴ y = x2 + x + 1
∴ x2 + x + 1 - y = 0
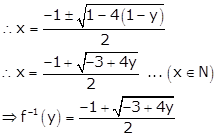
Hence, ![]()
Solution 19
Given: f: R+→ (7, ∞) given by f(x) = 16x2 + 24x + 7
As f is a bijective function, so it is invertible.
Let y = f(x)
∴ y = 16x2 + 24x + 7
∴ 16x2 + 24x + 7 - y = 0
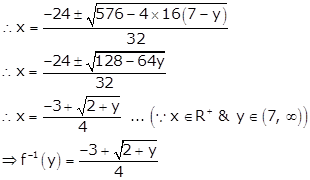
Hence, ![]()
Solution 1

Thus, h is a bijection and is invertible.
Solution 2(i)

Solution 2(ii)

Solution 3


Solution 4

∴ f-1 = {(3, 1), (5, 2), (7, 3), (9, 4)}
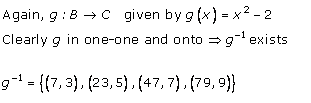
f-1 0g-1 = {(7, 1), (23, 2), (47, 3), (79, 4)} ……. (A)
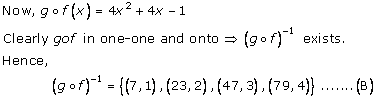
Now (A) & (B) we have (g0f)-1 = f-10g-1
Solution 5

Solution 6
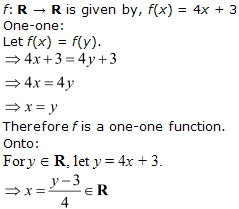
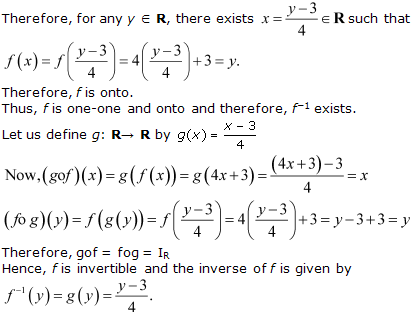
Solution 7

![]()
Solution 8

Solution 9
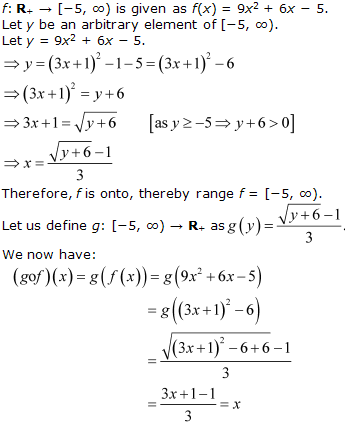
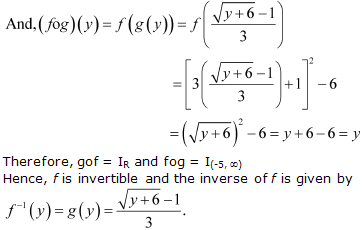
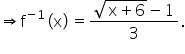
Solution 10

Solution 11

Solution 12
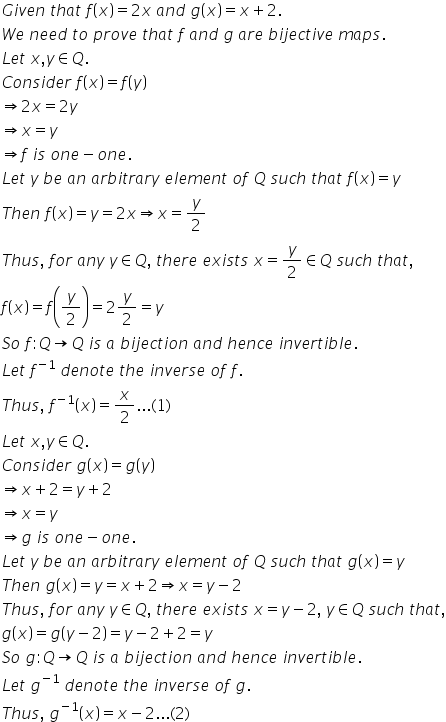
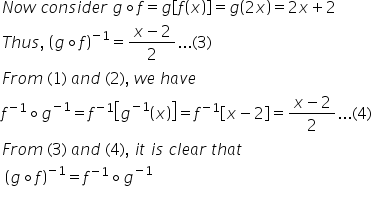
Solution 13
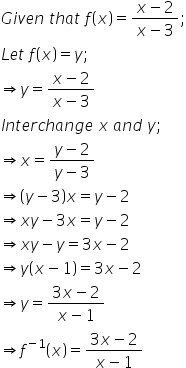
Solution 14

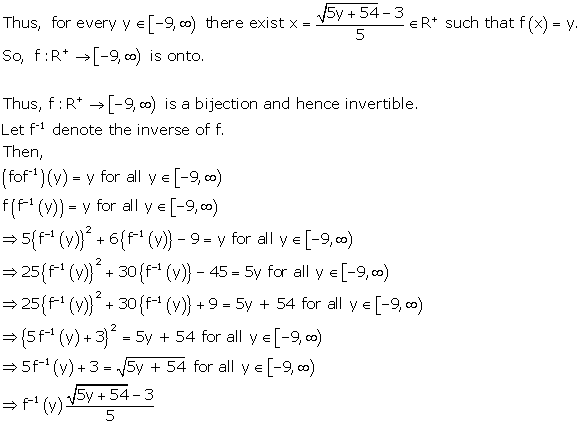
Solution 20

Solution 21

Solution 22


