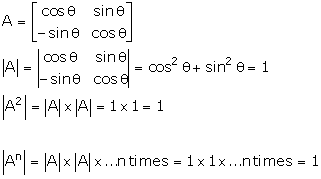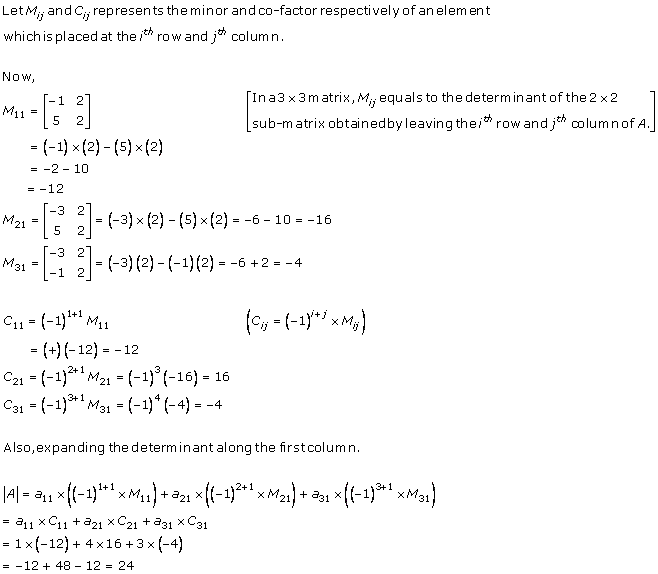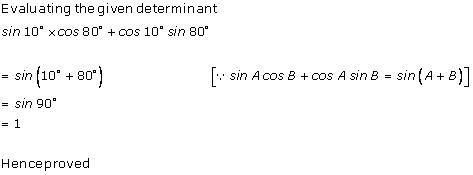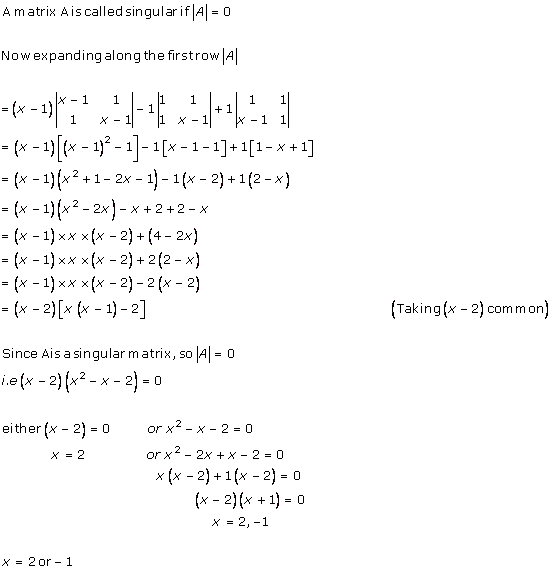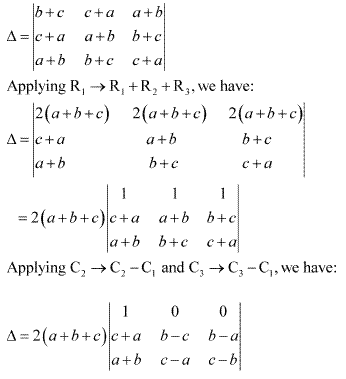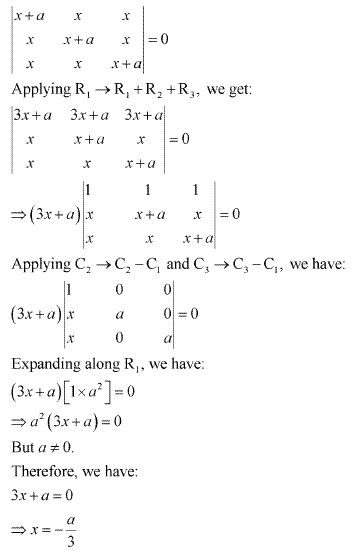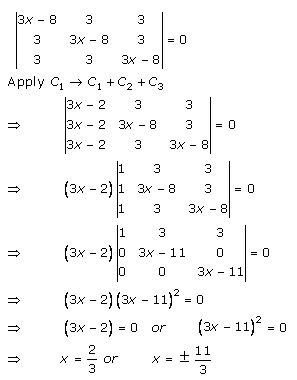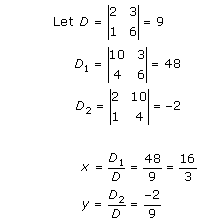Class 12-commerce RD SHARMA Solutions Maths Chapter 6 - Determinants
Determinants Exercise MCQ
Solution 34
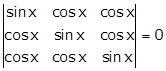
Applying C1→ C1 + C2 + C3

Applying R2→ R2 - R1 and R3→ R3 - R1
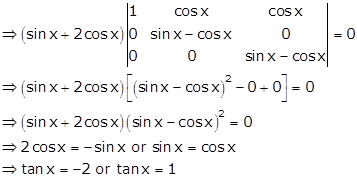
But tan x = -2 is
not possible as for ![]() we get
we get ![]()
Therefore, ![]()
![]()
Thus, only one real root exist.
Solution 35

Now,

![]()
Hence,  is equal to
0.
is equal to
0.
Solution 36
Area of a
triangle 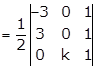
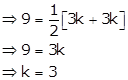
Solution 37
For any matrix A of order n × n, |kA| = kn|A| where k is a scalar
∴ |3A| = 33 |A| = 27 × 8 = 216
Solution 1
Correct option: (d)

Solution 2
Correct option: (d)

Solution 3
Correct option: (d)
If A is a square matrix of order n then det(A) = a11C11+a21C21+a31C31
Solution 4
Correct option: (b)
Minor of an element can never be equal to cofactor of the same element.
Cij=(-1)i+jMij
Solution 5
Correct option: (e)
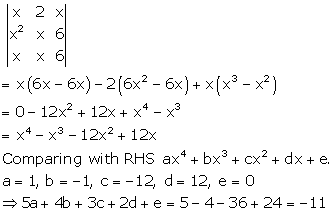
Solution 6
Correct option: (a)
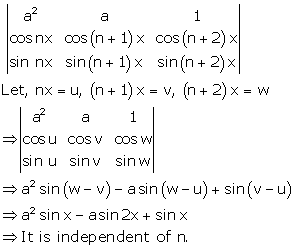
Solution 7
Correct option: (a)
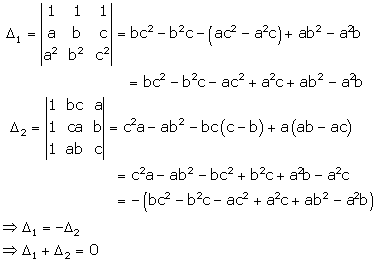
Solution 8

Solution 9
Correct option: (a)

Solution 10
Correct option: (a)

Solution 11
Correct option: (d)

Solution 12
Correct option: (b)
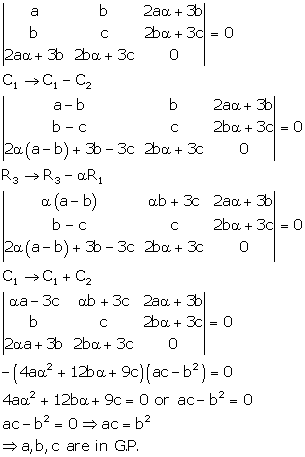
Solution 13
Correct option: (a)

Solution 14
Correct option: (c)
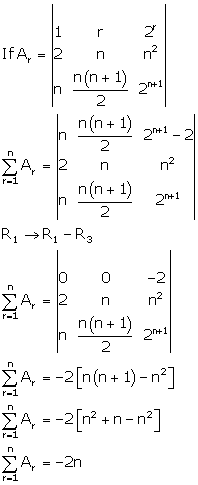
Solution 15
Correct option: (c)
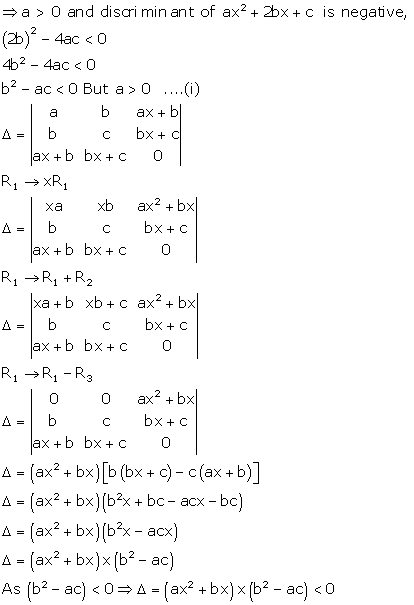
Solution 16
Correct option: (b)

Solution 17
Correct option: (b)
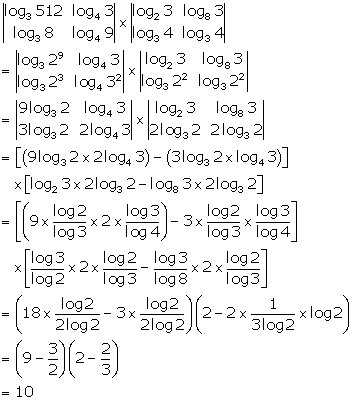
Solution 18
Correct option:(a)
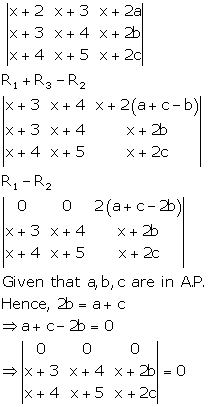
Solution 19
Correct option: (a)

Solution 20
Correct option: (b)
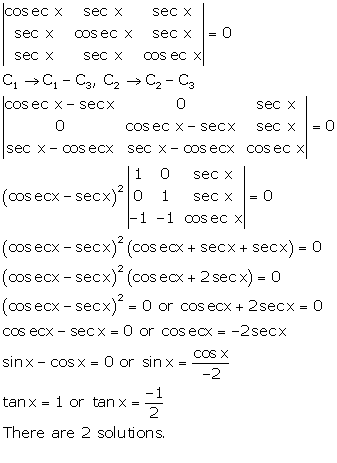
Solution 21
Correct option: (d)
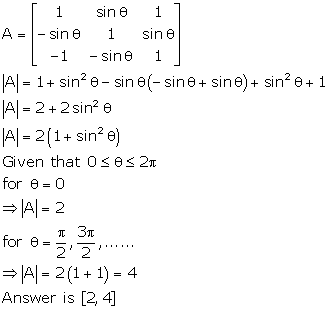
Solution 22
Correct option: (c)
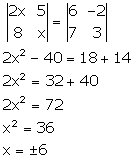
Solution 23
Correct option: (a)
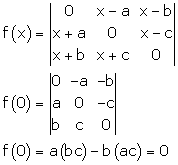
Solution 24
Correct option: (c )
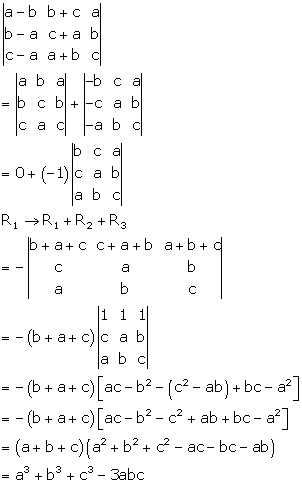
Solution 25
Correct option: (d)
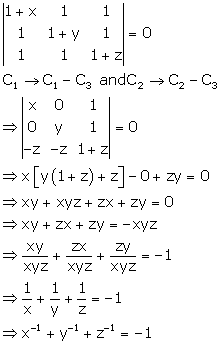
Solution 26
Correct option: (d)
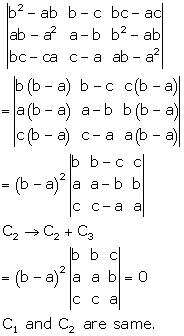
Solution 27
Correct option: (a)
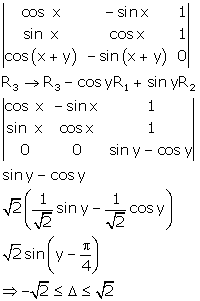
Solution 28
Correct option: (a)
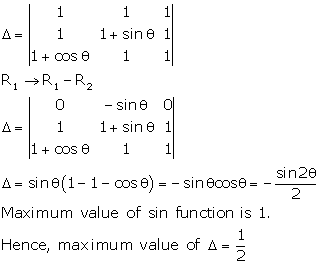
Solution 29
Correct option: (b)

Solution 30
Correct option: (a)
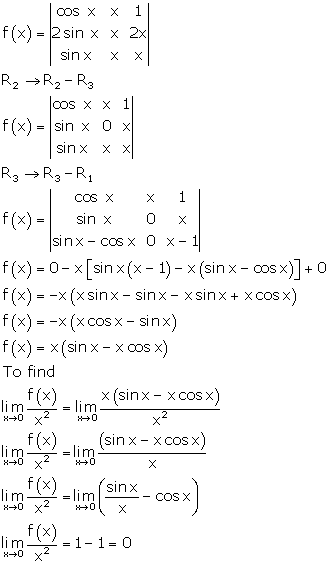
Solution 31
Correct option: (c)
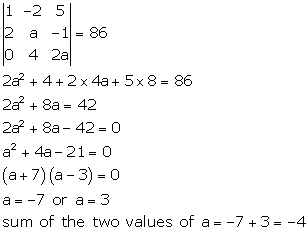
Solution 32
Correct option: (d)
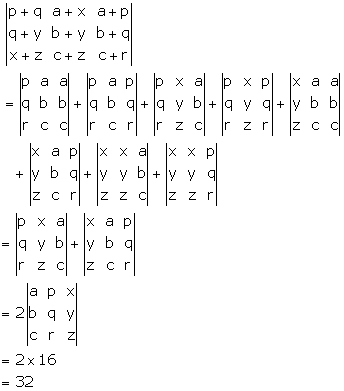
Solution 33
Correct option: (c)

Determinants Exercise Ex. 6.1
Solution 1(i)
Solution 1(ii)
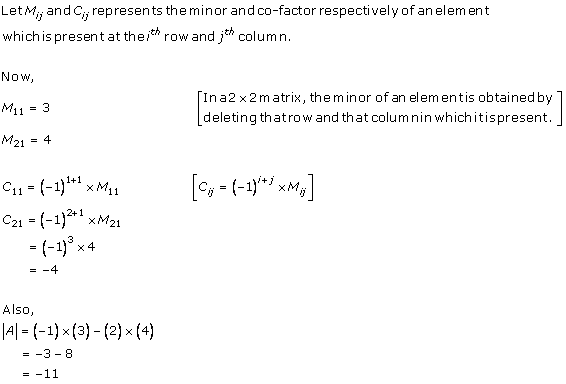
Solution 1(iii)
Solution 1(iv)
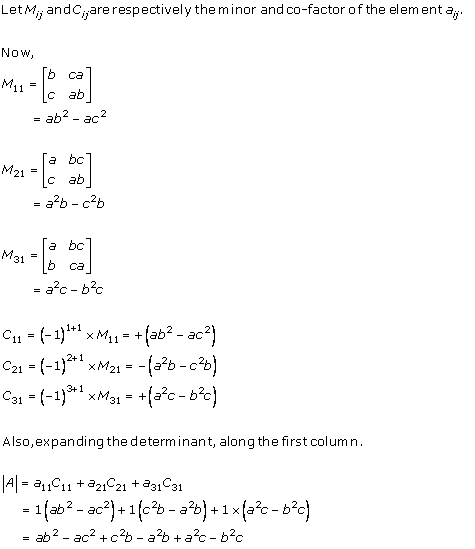
Solution 1(v)
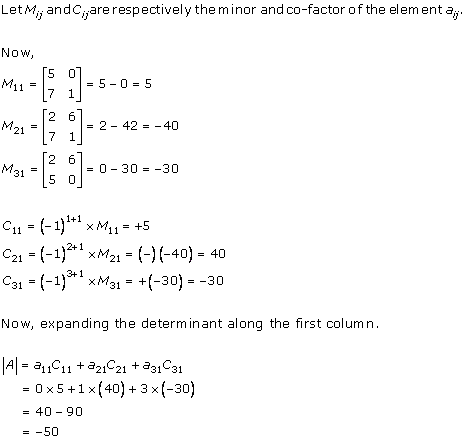
Solution 1(vi)
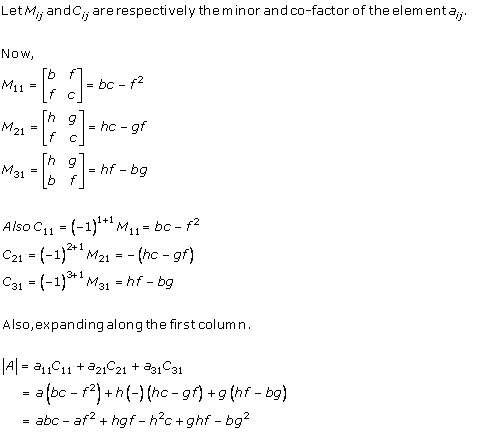
Solution 1(vii)

Solution 2 (i)
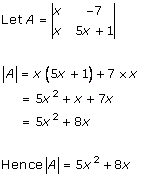
Solution 2 (ii)
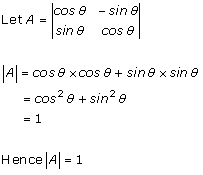
Solution 2 (iii)
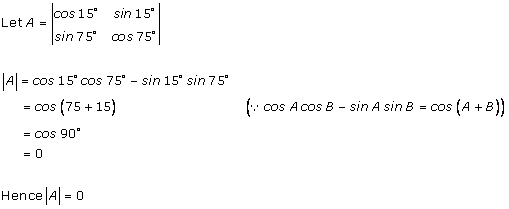
Solution 2 (iv)
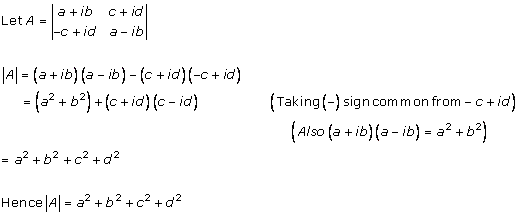
Solution 3
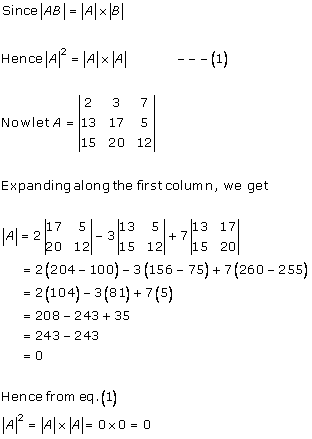
Solution 4
Solution 5
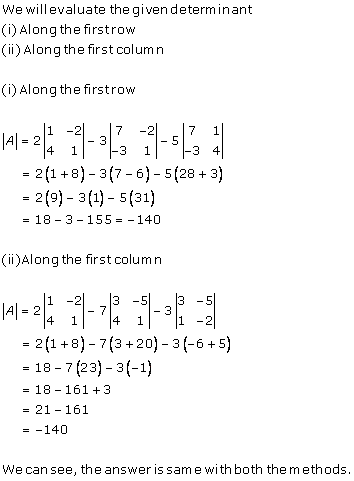
Solution 6
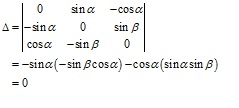
Solution 7
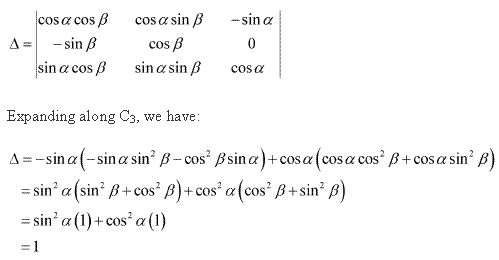
Solution 8
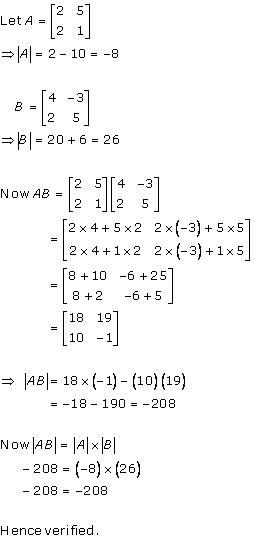
Solution 9

Solution 10


Solution 10(v)
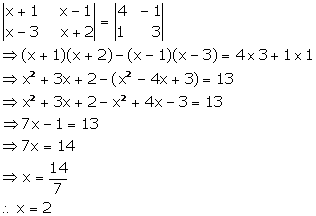
Solution 10(vi)
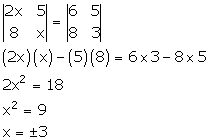
Solution 11
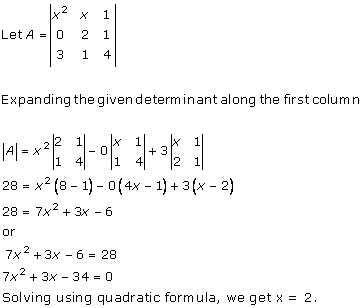
Solution 12(i)
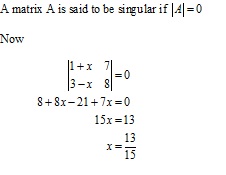
Solution 12(ii)
Solution 10(i)
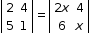
⇒ 2 × 1 - 5 × 4 = 2x × x - 6 × 4
⇒ 2 - 20 = 2x2 - 24
⇒ 2x2 = 6
⇒ x2 = 3
⇒ x = 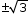
Determinants Exercise Ex. 6.2
Solution 1(i)
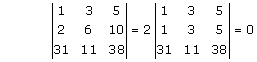
Solution 1(ii)
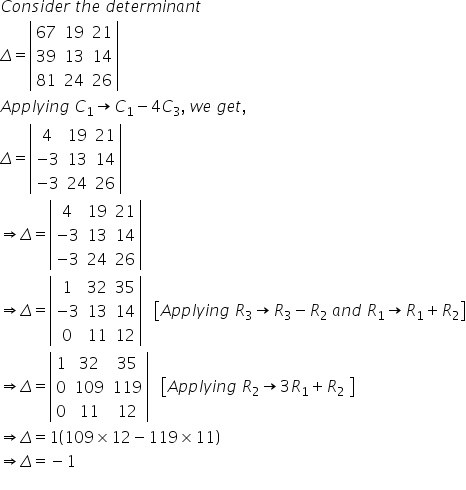
Solution 1(iii)
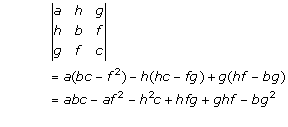
Solution 1(iv)
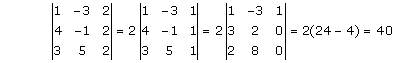
Solution 1(v)
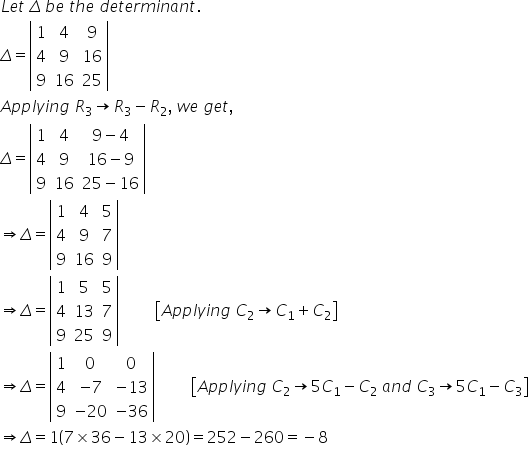
Solution 1(vi)

Solution 1(vii)

Solution 1(viii)

Solution 2(i)

Solution 2(ii)

Solution 2(iii)

Solution 2(iv)

Solution 2(v)
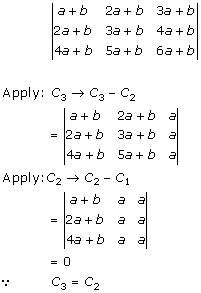
Solution 2(vi)
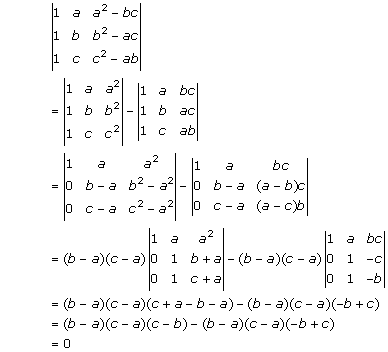
Solution 2(vii)
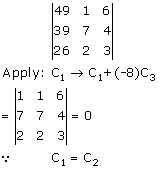
Solution 2(viii)

Solution 2(ix)
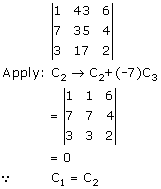
Solution 2(x)

Solution 2(xi)
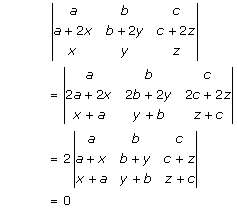
Solution 2(xii)
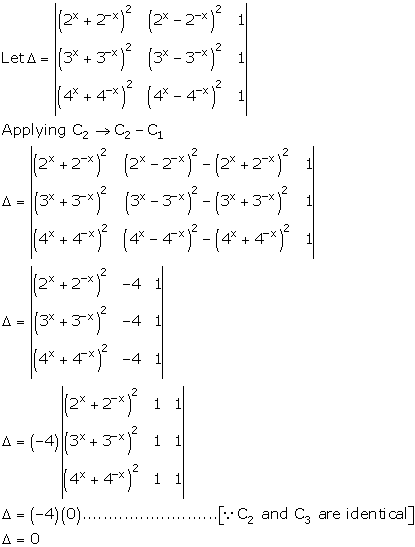
Solution 2(xiii)

Solution 2(xiv)

Solution 2(xv)
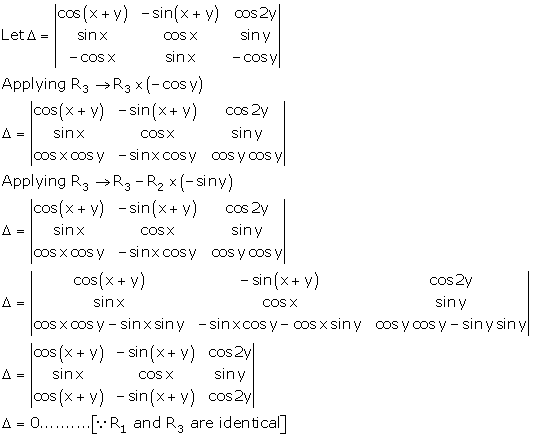
Solution 2(xvi)

Solution 2(xvii)
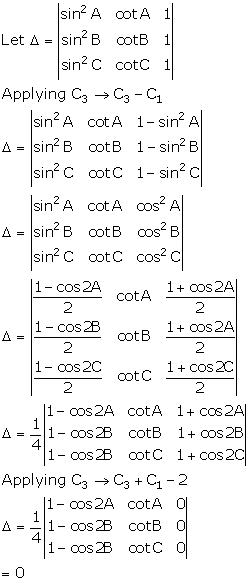
Solution 3

Solution 4
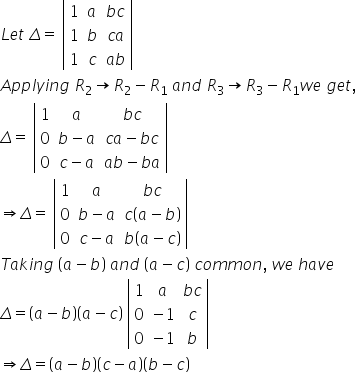
Solution 5
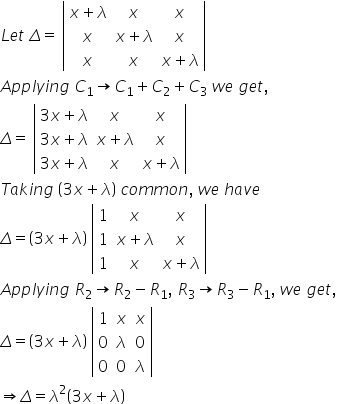
Solution 6

Solution 7
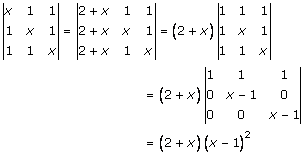
Solution 8
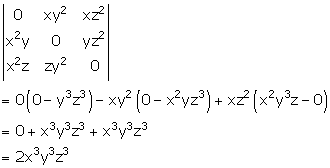
Solution 9

Solution 10

Solution 11

Solution 12

Solution 13

Solution 14

Solution 15
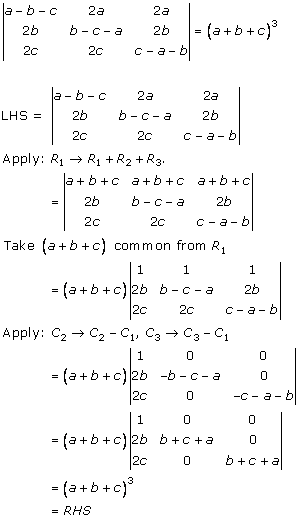
Solution 16

Solution 17

Solution 18
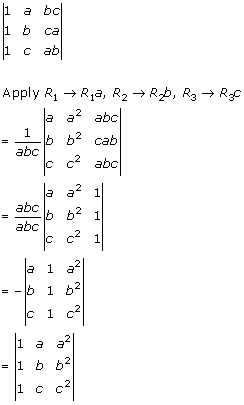
Solution 19

Solution 20

Solution 21

Solution 22

Solution 23

Solution 24


Solution 25

Solution 26
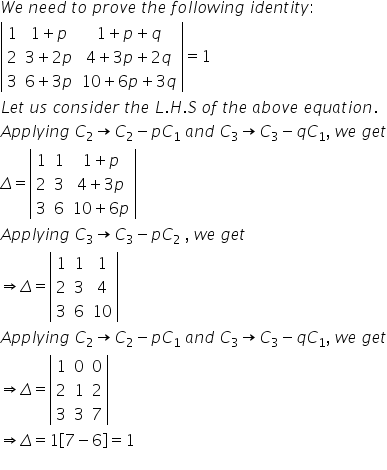
Solution 27

Solution 28

Solution 29

Solution 30

Solution 31

Solution 32

Solution 33

Solution 34
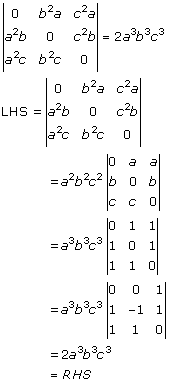
Solution 35
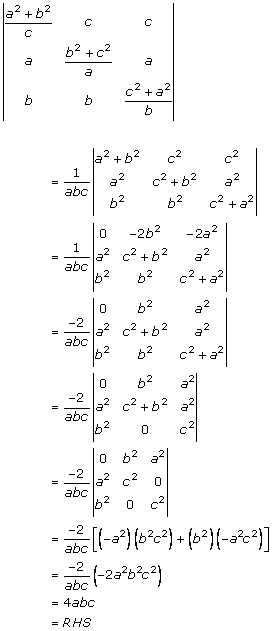
Solution 36

Solution 37

Solution 38

Solution 39
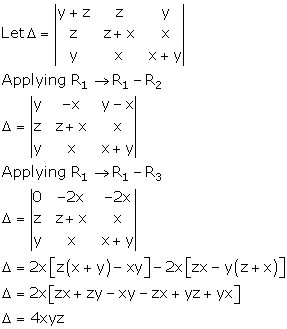
Solution 40

Solution 42

Solution 43

Solution 44

Solution 45
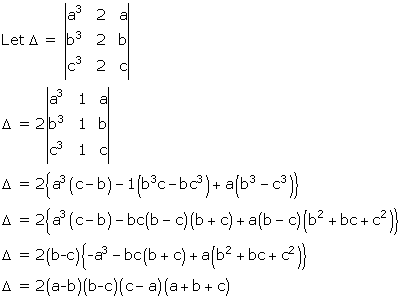
Solution 46

Solution 47

Solution 48

Solution 49

Solution 50
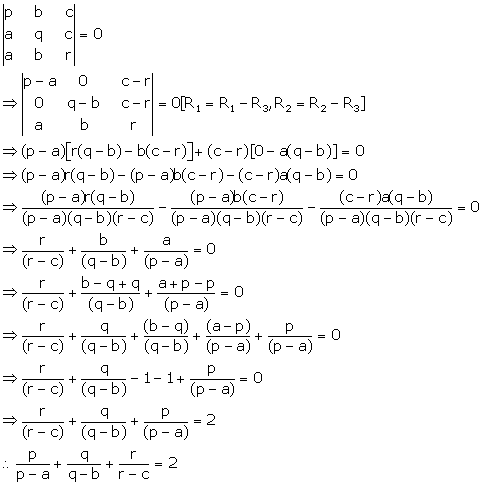
Solution 51
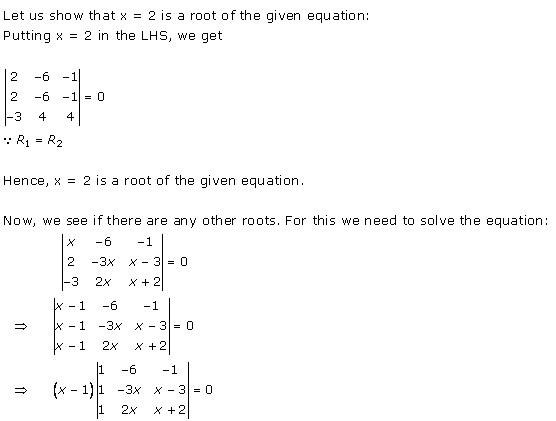
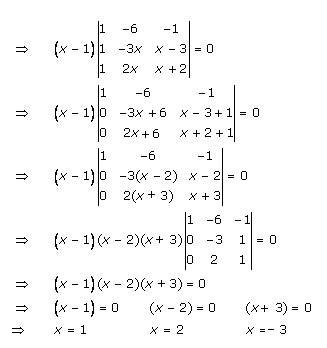
Solution 52(i)

Solution 52(ii)
Solution 52(iii)
Solution 52(v)

Solution 52(vi)
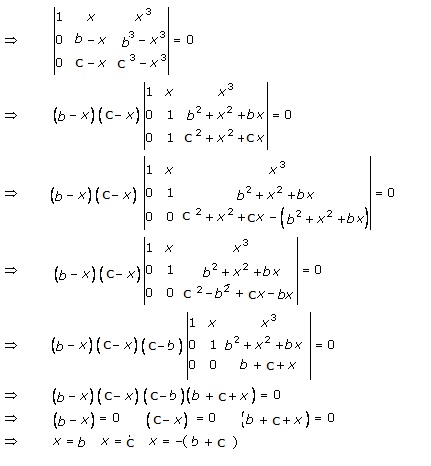
Solution 52(vii)
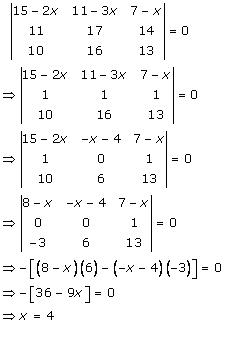
Solution 52(viii)
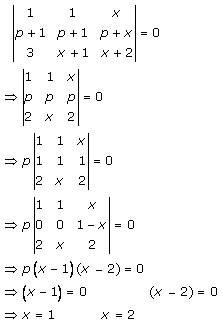
Solution 52(ix)

Solution 41
Consider the determinant
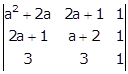
Applying R1→ R1 - R2 and R2→ R2 - R3
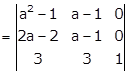
Taking (a - 1) common from R1 and R2
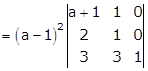
Now expanding this determinant along C3
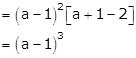
Solution 52(iv)
Given: 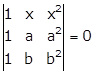
Applying R1→ R1 - R3
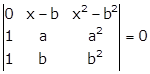
Applying R2→ R2 - R3
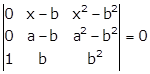
Taking (x - b) and (a - b) common from R1 and R2 respectively
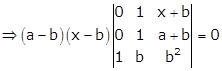
Expanding along C1, we get
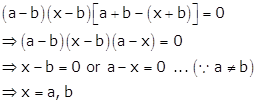
Solution 52(x)
Given: 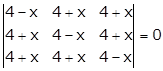
Applying C1→ C1 + C2 + C3
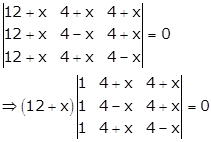
Applying R1→ R1 - R3 and R2→ R2 - R3
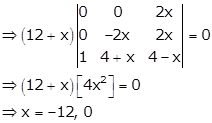
Solution 53
Given: 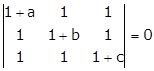
Applying C1→ C1 - C2
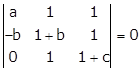
Applying C2→ C2 - C3
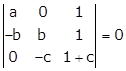
Expanding this determinant along R1, we get
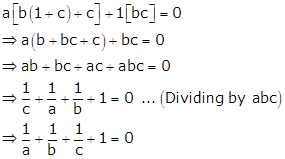
Solution 54
Given: 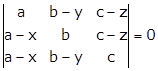
Applying R2→ R2 - R1

Applying R3→ R3 - R1
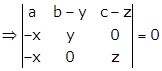
Expanding this determinant along C3, we get
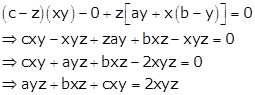
Dividing throughout by xyz, we get
![]()
Hence, the value
of ![]() is 2.
is 2.
Solution 55
Consider the
determinant 
Applying R2→ R2 - R3
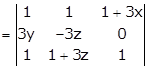
Applying R1→ R1 - R3
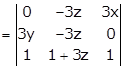
Taking 3 common from R1 and R2
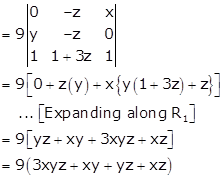
Hence, 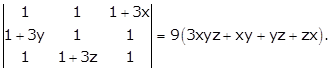
Determinants Exercise Ex. 6.3
Solution 1 (i)

Solution 1 (ii)
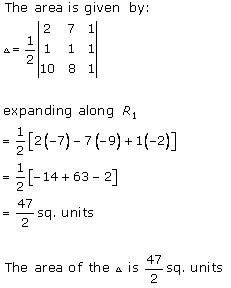
Solution 1 (iii)
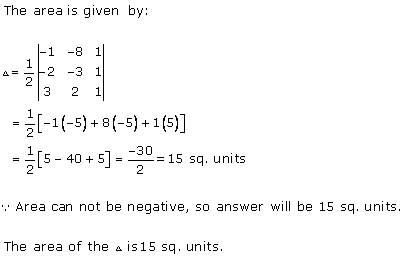
Solution 1 (iv)
Solution 2 (i)

Solution 2(ii)

Solution 2 (iii)
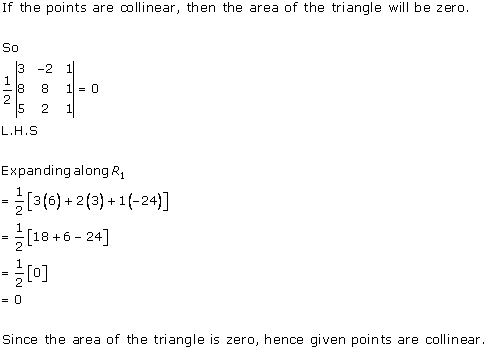
Solution 2 (iv)

Solution 3

Solution 4
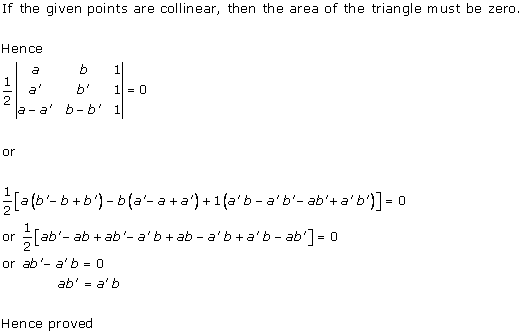
Solution 5
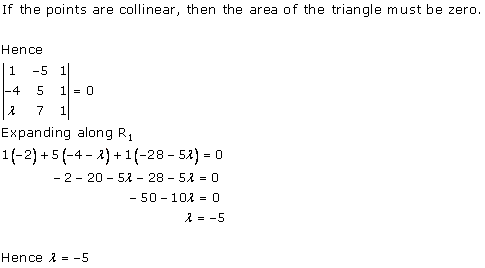
Solution 6

Solution 7
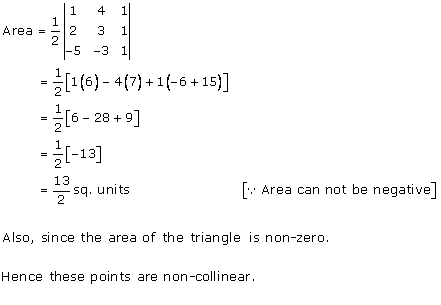
Solution 8

Solution 9
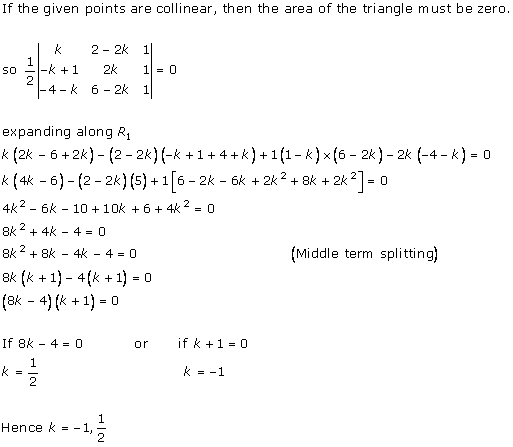
Solution 10
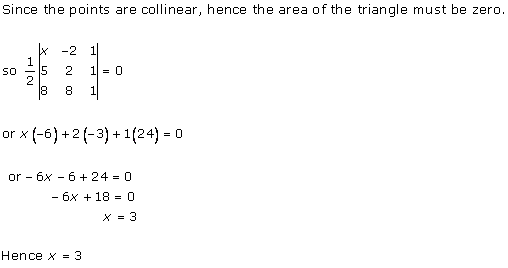
Solution 11
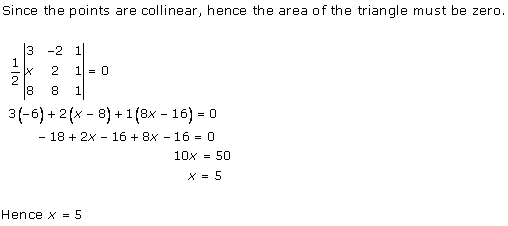
Solution 12 (i)

Solution 12 (ii)

Solution 13 (i)
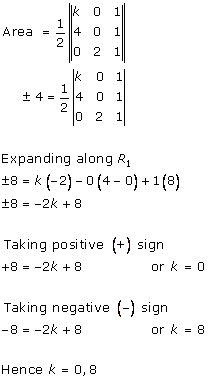
Solution 13 (ii)

Determinants Exercise Ex. 6.4
Solution 1
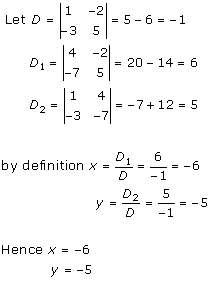
Solution 2
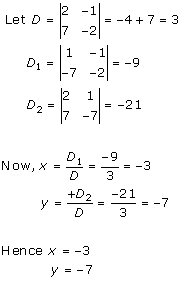
Solution 3
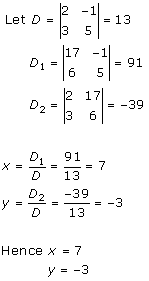
Solution 4
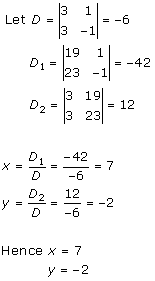
Solution 5
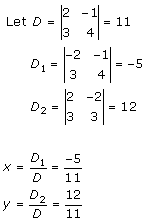
Solution 6

Solution 7
Solution 8
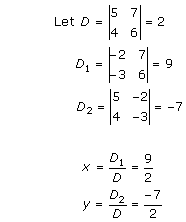
Solution 9
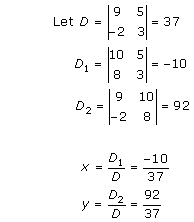
Solution 10
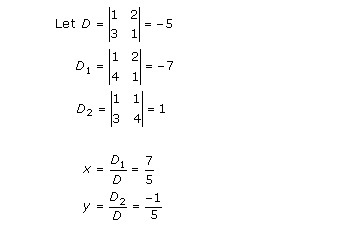
Solution 11

Solution 12
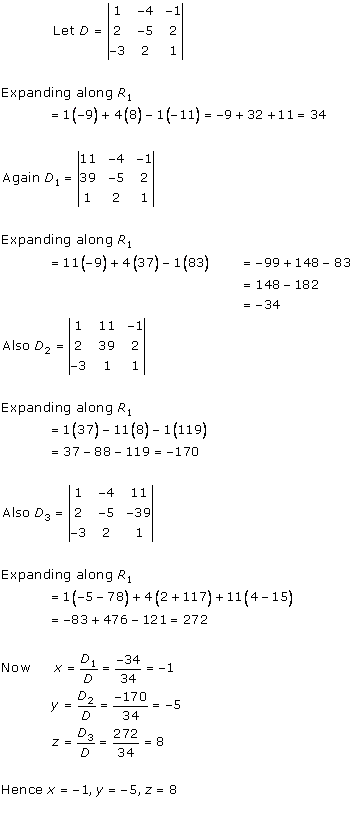
Solution 13
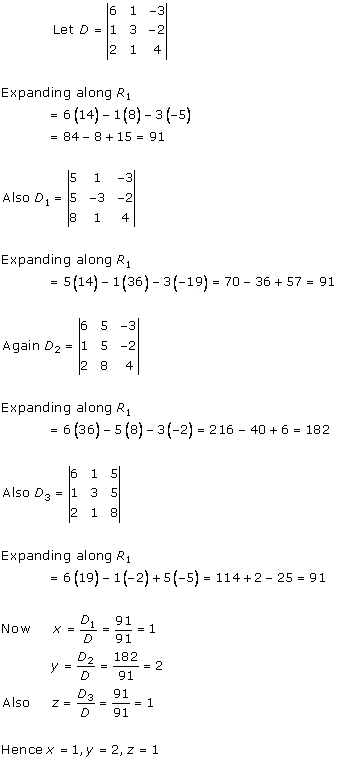
Solution 14
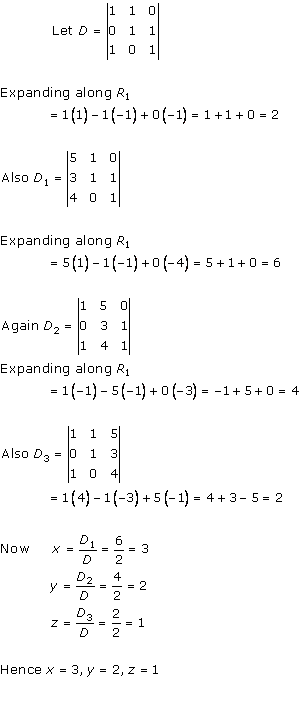
Solution 15

Solution 16

Solution 17

Solution 18
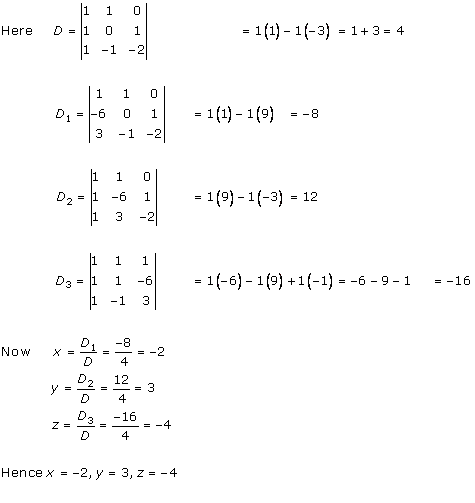
Solution 19
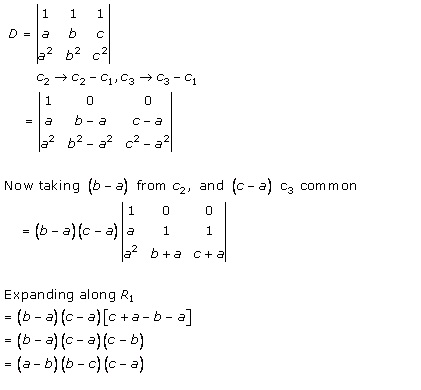


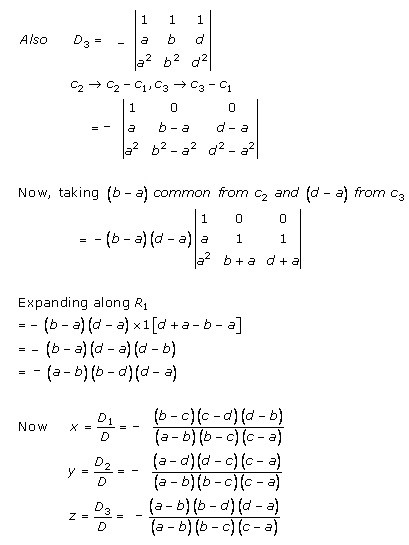
Solution 20

Solution 21

Solution 22
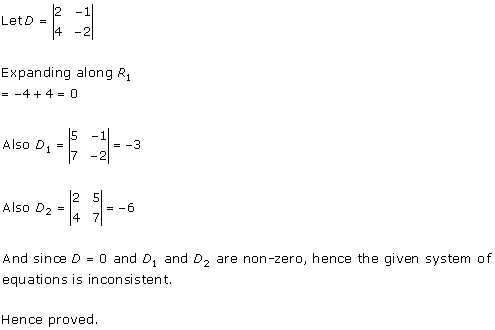
Solution 23

Solution 24
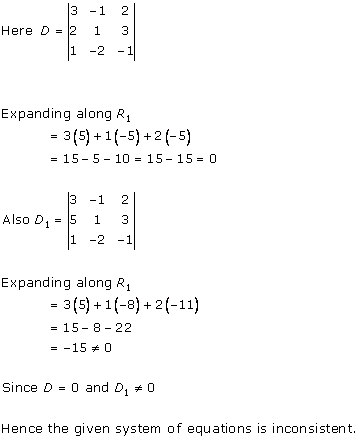
Solution 25
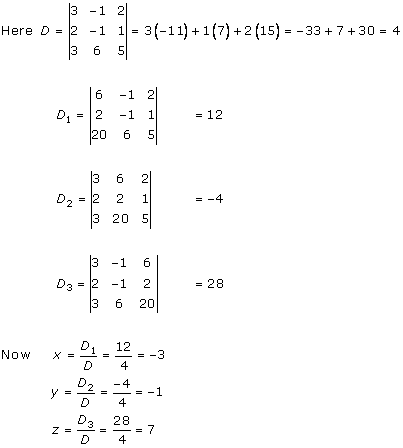
Solution 26

Solution 27

Solution 28

Solution 29

Solution 30

Solution 31

Solution 32

Determinants Exercise Ex. 6.5
Solution 1

Solution 2
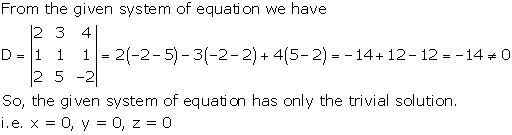
Solution 3
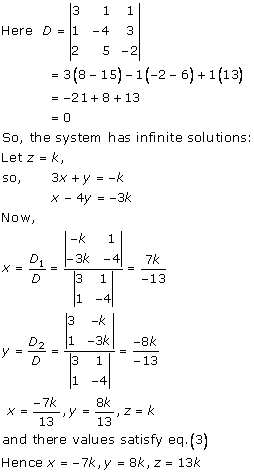
Solution 4

Solution 5
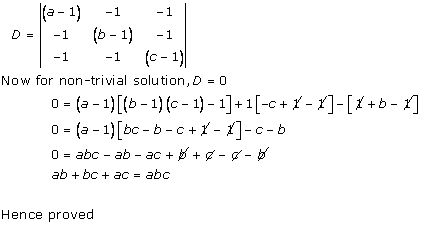
Determinants Exercise Ex. 6VSAQ
Solution 53
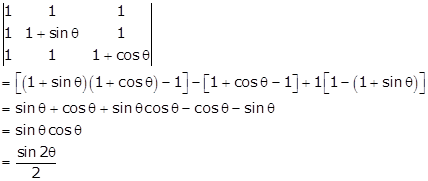
We know that,
maximum value of sin is 1 as ![]()
![]()
Solution 54
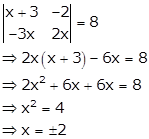
Solution 55
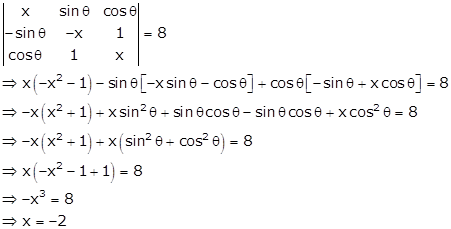
Solution 56
Given: Det (A-1) = (Det A)k
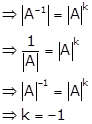
Solution 57
Given: AB = 2I
|AB| = |2I|
|B| |A| = 23 |I|
2|B| = 8
∴ |B| = 4
Solution 58
A square matrix A is said to be singular, if its determinant is 0, i.e. |A| = 0.
Solution 1
![]()
Solution 2
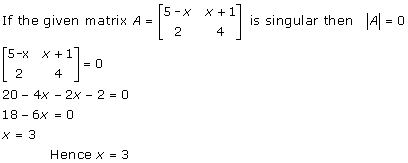
Solution 3

Solution 4
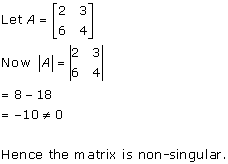
Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10

Solution 11

Solution 12
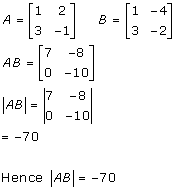
Solution 13
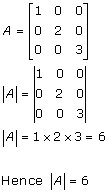
Solution 14

Solution 15
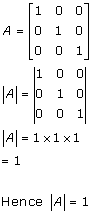
Solution 16

Solution 17

Solution 18
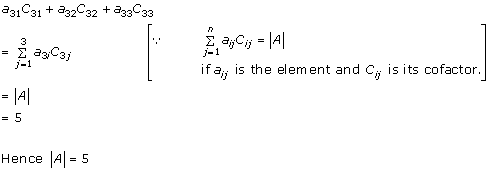
Solution 19

Solution 20
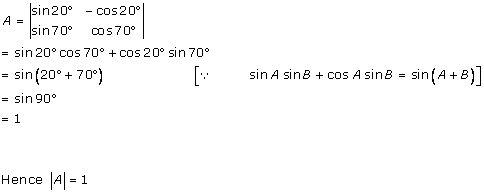
Solution 21

Solution 22

Solution 23

Solution 24
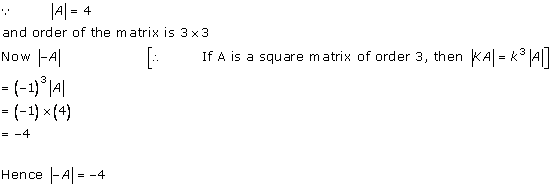
Solution 25
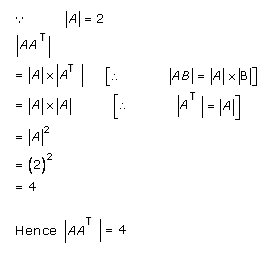
Solution 26

Solution 27

Solution 28
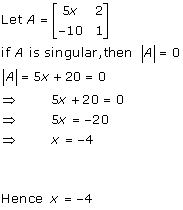
Solution 29

Solution 30

Solution 31

Solution 32

Solution 33

Solution 34

Solution 35

Solution 36

Solution 37
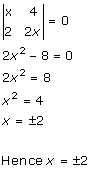
Solution 38

Solution 39

Solution 40

Solution 41

Solution 42

Solution 43
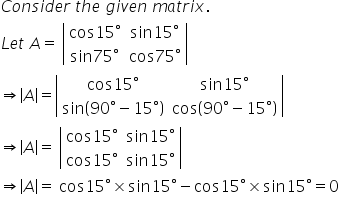
Solution 44
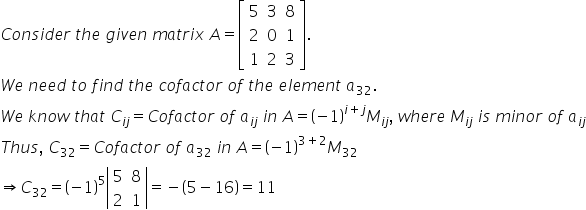
Solution 45
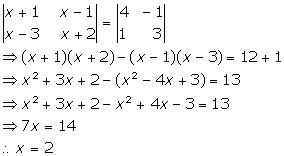
Solution 46

Solution 47
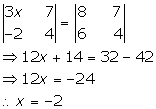
Solution 48
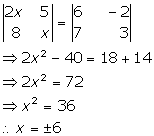
Solution 49
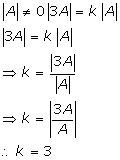
Solution 50
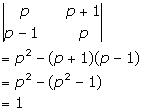
Solution 51
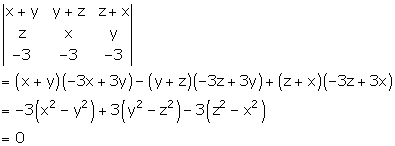
Solution 52