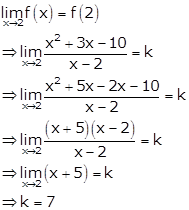Class 12-commerce RD SHARMA Solutions Maths Chapter 9: Continuity
Continuity Exercise Ex. 9.1
Solution 1

Solution 2

Solution 3

Solution 4

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10(i)

Solution 10(ii)

Solution 10(iii)

Solution 10(iv)

Solution 10(v)

Solution 10(vi)

Solution 10(vii)
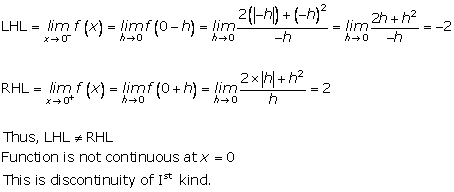
Solution 10(viii)

Solution 11

Solution 12

Solution 13
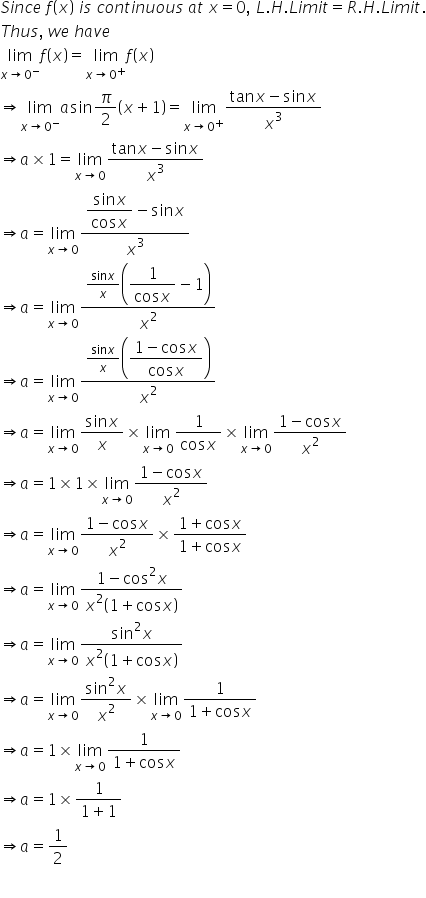
Solution 14

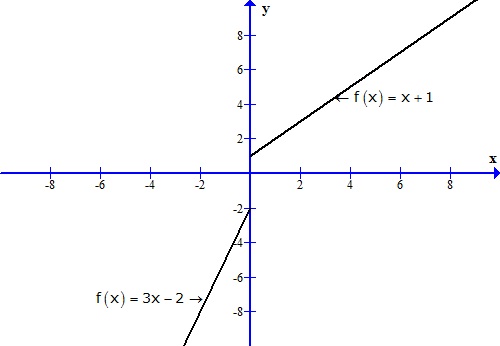
Solution 15

Solution 16

Solution 17

Solution 18

Solution 19

Solution 20

Solution 21

Solution 22
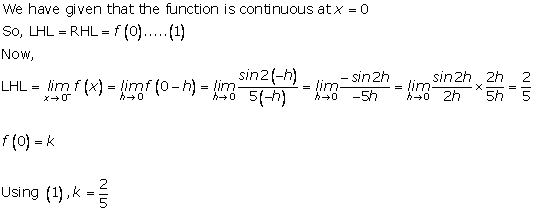
Solution 23

Solution 24

Solution 25

Solution 26


Solution 27

Solution 28

Solution 29
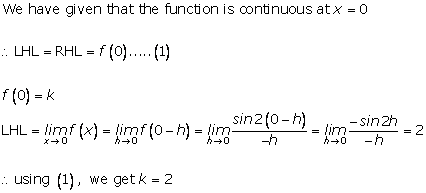
Solution 30

Solution 31

Solution 32

Solution 33

Solution 34

Solution 35

Solution 36(i)

Solution 36(ii)
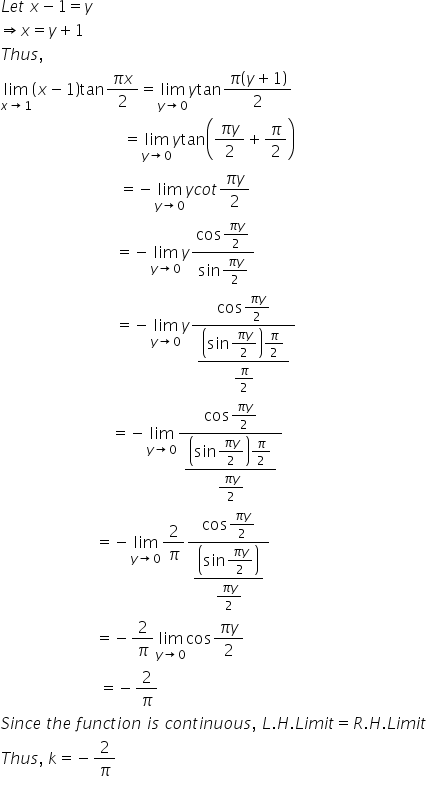
Solution 36(iii)

Solution 36(iv)

Solution 36(v)

Solution 36(vi)
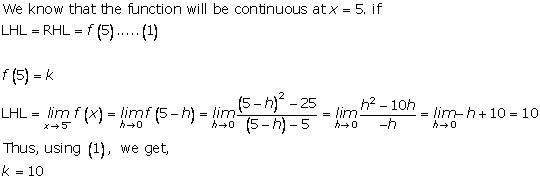
Solution 36(vii)

Solution 36(viii)

Solution 36(ix)

Solution 37

Solution 38

Solution 39(i)

Solution 39(ii)

Solution 40

Solution 41

Solution 42
Given: 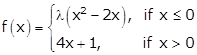
At x = 0, we have
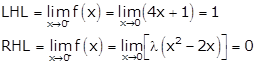
∴ LHL ≠ RHL
So, f(x) is discontinuous at x = 0.
Thus, there is no
value of ![]() for which
f(x) is continuous at x = 0.
for which
f(x) is continuous at x = 0.
At x = 1, we have

∴ LHL = RHL
So, f(x) is continuous at x = 1.
At x = -1, we have
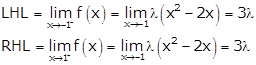
∴ LHL = RHL
So, f(x) is continuous at x = -1.
Solution 43

Solution 44


Solution 45

Solution 46
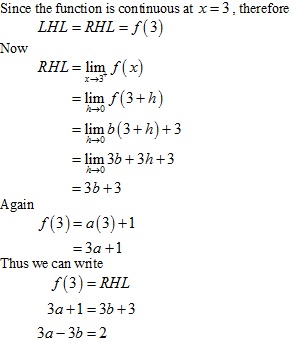
Continuity Exercise Ex. 9.2
Solution 1

Solution 2
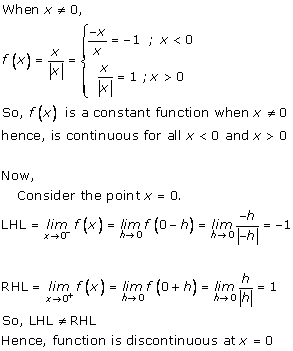
Solution 3(i)

Solution 3(ii)


Solution 3(iii)

Solution 3(iv)

Solution 3(v)
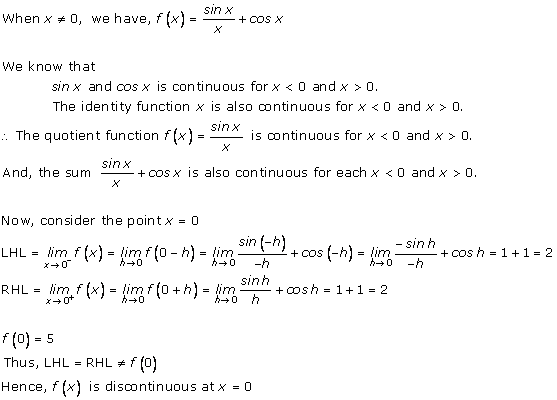
Solution 3(vi)

Solution 3(vii)

Solution 3(viii)

Solution 3(ix)


Solution 3(x)



Solution 3(xi)



Solution 3(xii)


Solution 3(xiii)



Solution 4(i)
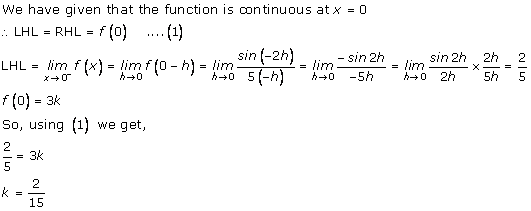
Solution 4(ii)

Solution 4(iii)

Solution 4(iv)

Solution 4(v)

Solution 4(vi)

Solution 4(vii)


Solution 4(viii)
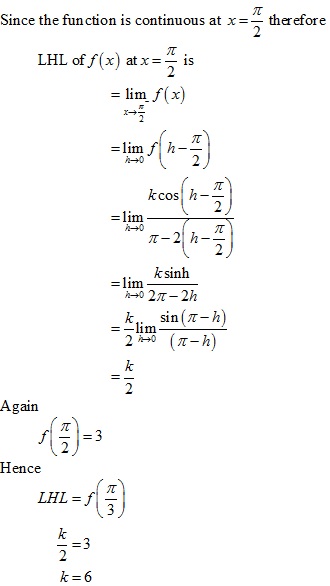
Solution 5

Solution 6


Solution 7

Solution 8

Solution 9

Solution 10

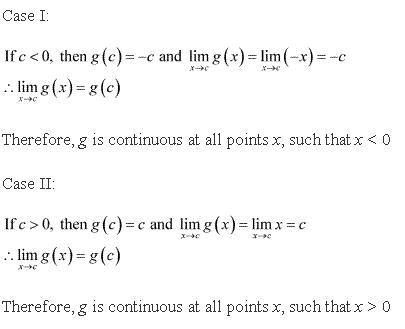


Solution 11

Solution 12

Solution 13


Solution 14


Solution 15




Solution 16

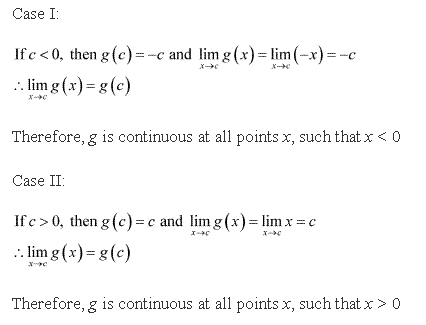

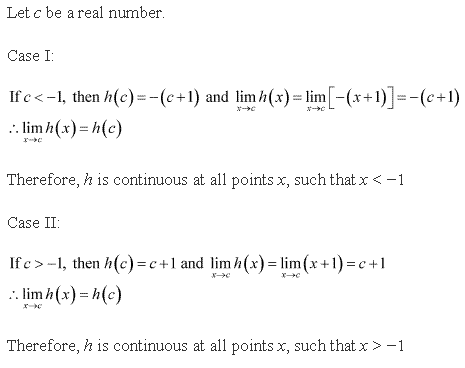

Solution 17


Solution 18

Solution 19

Continuity Exercise MCQ
Solution 1
Correct option: (c)

Solution 2
Correct option: (a), (b)
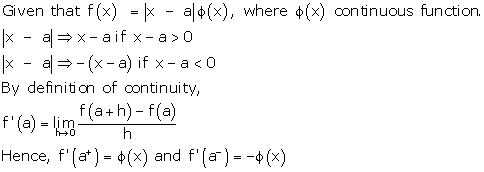
Solution 3
Correct option: (a),(d)
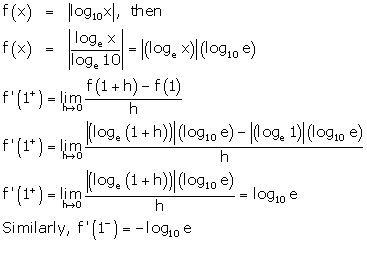
Solution 4
Correct option: (c)
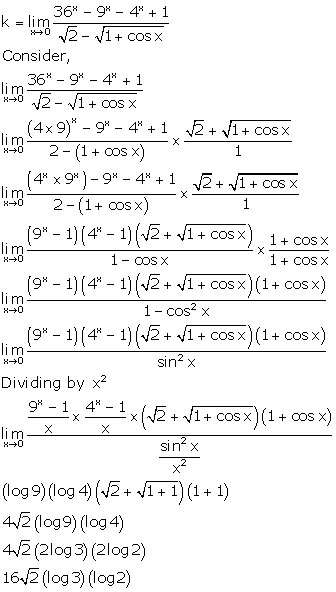
Solution 5
Correct option: (d)
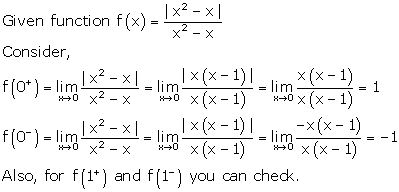
Solution 6
Correct option: (c)

Solution 7
Correct option: (c)
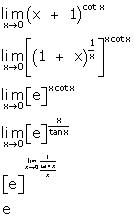
Solution 8
Correct option: (b)
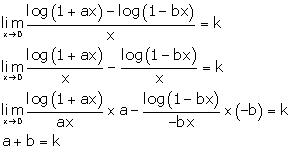
Solution 9
Correct option: (b)
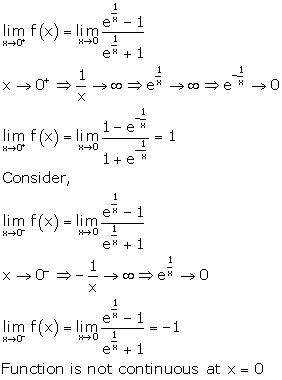
Solution 10
Correct option: (d)
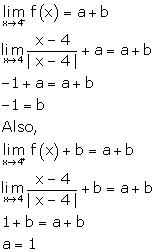
Solution 11
Correct option: (b)

Solution 12
Correct option: (a)
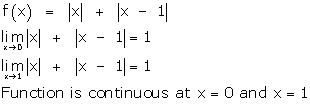
Solution 13
Correct option: (d)
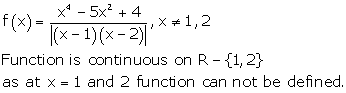
Solution 14
Correct option: (c)
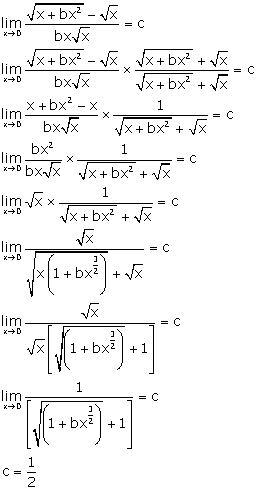
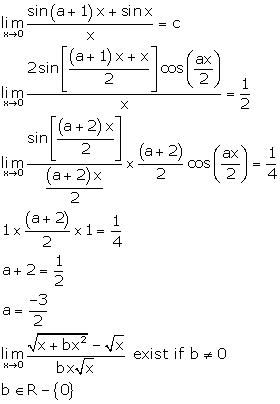
Solution 15
Correct option: (c)
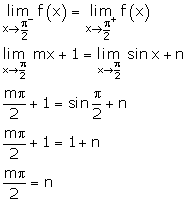
Solution 16
Correct option: (c)
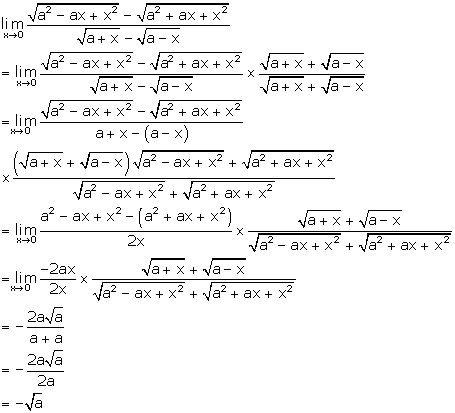
Solution 17
Correct option: (c)
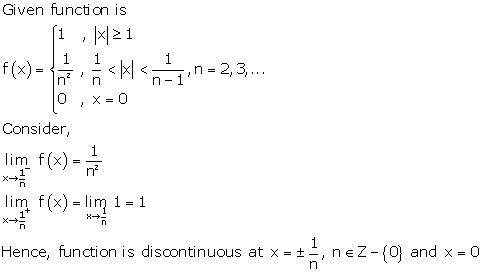
Solution 18
Correct option: (c)
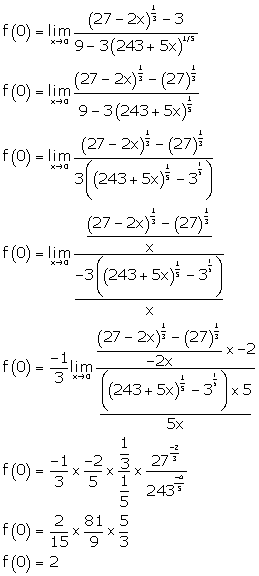
Solution 19
Correct option: (d)
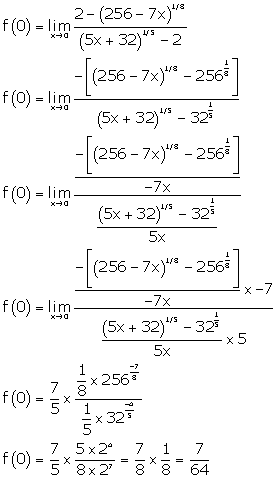
Solution 20
Correct option: (b)
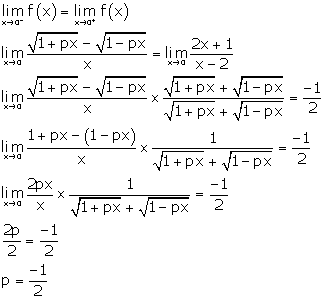
Solution 21
Correct option: (a)

Solution 22
Correct option: (a)

Solution 23
Correct option:(d)
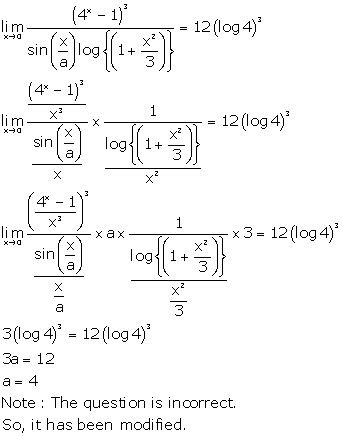
Solution 24
Correct option: (c)
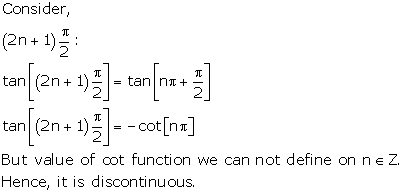
Solution 25
Correct option: (b)
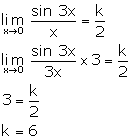
Solution 26
Correct option: (b)
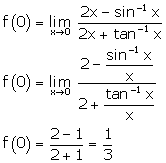
Solution 27
Correct option: (a)

Solution 28
Correct option: (a)
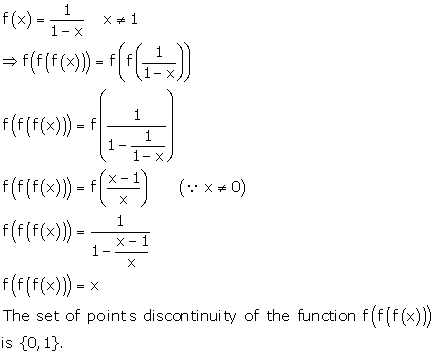
Solution 29
Correct option: (b)
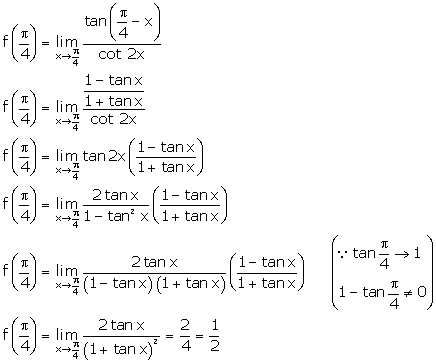
Solution 30
Correct option: (a)

Solution 31
Correct option: (a)
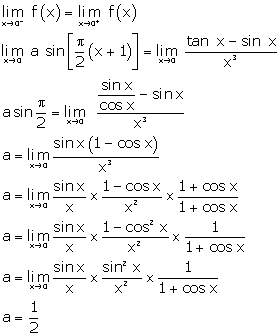
Solution 32
Correct option: (d)

Solution 33
Correct option: (b)
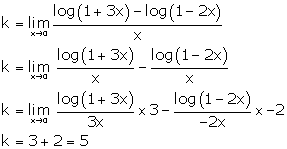
Solution 34
Correct option: (b)
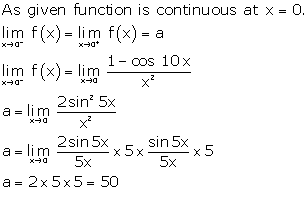
Solution 35
Correct option: (a)
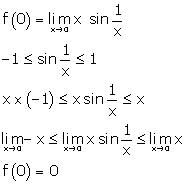
Solution 36
Correct option: (d)
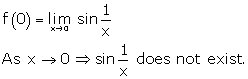
Solution 37
Correct option: (c)
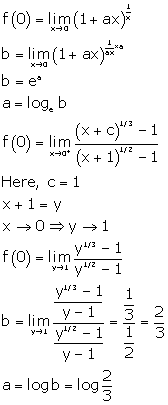
Solution 38
Correct option: (b)
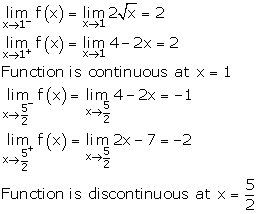
Solution 39
Correct option: (b)
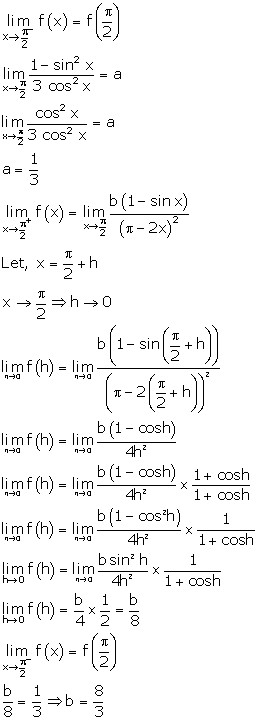
Solution 40
Correct option: (b)
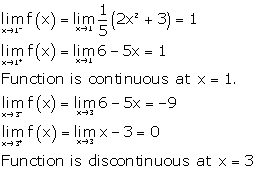
Solution 41
Correct option: (d)

Solution 42
Correct option: (a)

Solution 43
We know that, if f(x) and g(x) are continuous then
[f(x) + g(x)], [f(x) - g(x)], f(x)g(x) are continuous functions.
Now, 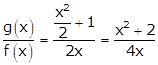
For f(x) = 0
∴ 4x = 0
∴ x = 0
Thus, ![]() is
discontinuous at x =0.
is
discontinuous at x =0.
Solution 44
The function f(x) = cot x is discontinuous if cot x → ∞
![]()
Solution 45
Given: ![]()
As f(x) is continuous at x = 0, then
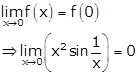
Hence, the value of f(x) is 0.
Solution 46
Given: ![]()
![]()
As {x} = 0 for integral values of x.
Therefore, domain of f(x) is set of all non-integral values.
Thus, f(x) is discontinuous at all integers.
Solution 47
The function f(x) = [x] is continuous everywhere except for integral values.
Therefore, f(x) = [x] is continuous at x = 1.5.
Solution 48
Given: 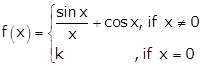
As f(x) is continuous at x = 0, we have
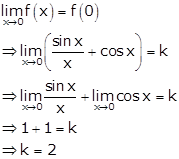
Continuity Exercise Ex. 9VSAQ
Solution 1

Solution 2
![]()
Solution 3
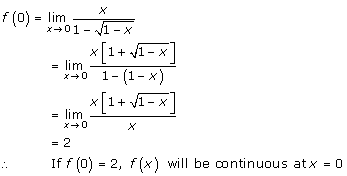
Solution 4

Solution 5
![]()
Solution 6
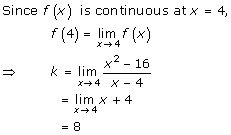
Solution 7

Solution 8
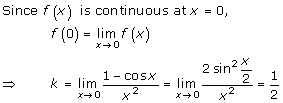
Solution 9
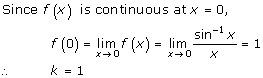
Solution 10

Solution 11
Given: 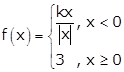
As f(x) is continuous at x = 0, we have
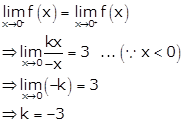
Solution 12
Given: 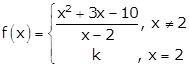
As f(x) is continuous at x = 2, we have