Class 11-commerce RD SHARMA Solutions Maths Chapter 1 - Sets
Ex. 1.1
Ex. 1.6
Ex. 1.7
Ex. 1.2
Ex. 1.3
Ex. 1.4
Ex. 1.5
Ex. 1.8
Ex. 1VSAQ
Sets Exercise Ex. 1.1
Solution 1

Solution 2

Solution 3
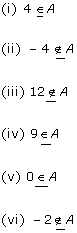
Sets Exercise Ex. 1.6
Solution 2(i)

Solution 2(ii)

Solution 2(iii)
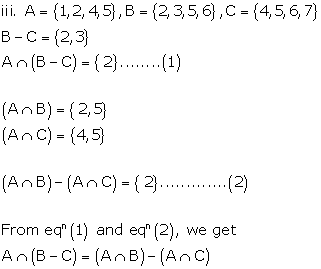
Solution 2(iv)
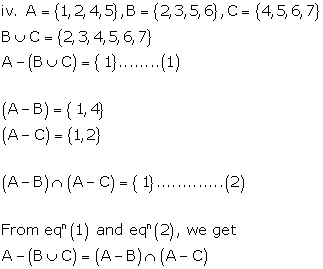
Solution 2(v)
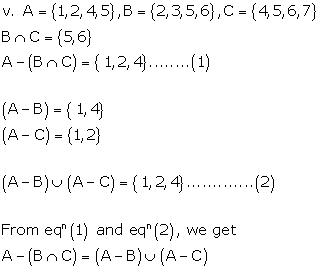
Solution 2(vi)

Solution 4(i)

Solution 4(ii)
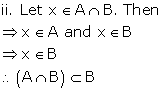
Solution 4(iii)
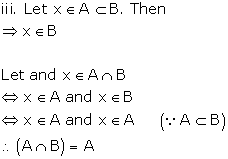
Solution 14(i)
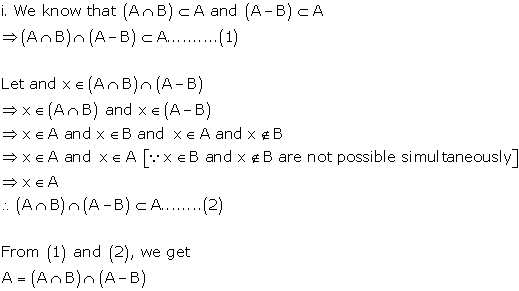
Solution 14(ii)

Solution 15
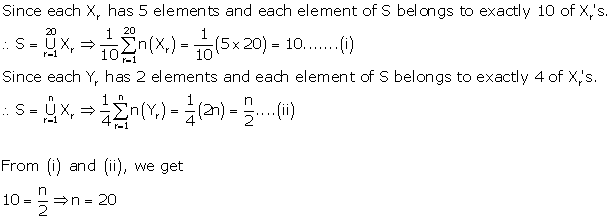
Solution 1

Solution 3(i)

Solution 3(ii)

Solution 5


Solution 6(i)
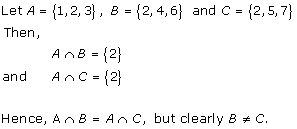
Solution 6(ii)

Solution 7

Solution 8

Solution 9

Solution 10

Solution 11
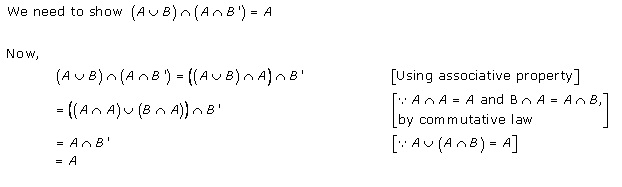
Solution 12(i)
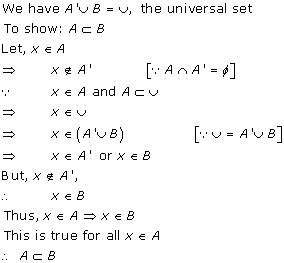
Solution 12(ii)
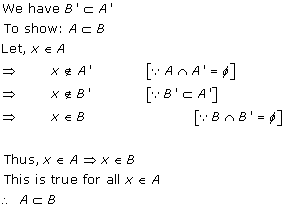
Solution 13

Sets Exercise Ex. 1.7
Solution 4(i)
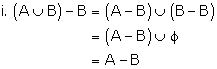
Solution 4(ii)
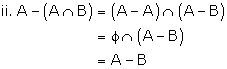
Solution 4(iii)

Solution 4(iv)

Solution 4(v)
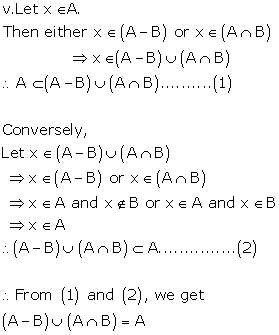
Solution 1

Solution 2(i)

Solution 2(ii)

Solution 2(iii)
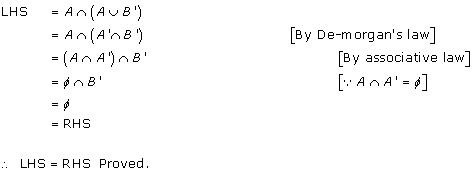
Solution 2(iv)

Solution 3
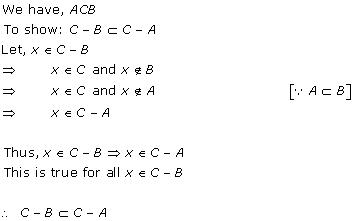
Sets Exercise Ex. 1.2
Solution 1(i)

Solution 1(ii)

Solution 1(iii)

Solution 1(iv)

Solution 1(v)

Solution 1(vi)

Solution 1(vii)

Solution 1(viii)

Solution 1(ix)

Solution 2(i)

Solution 2(ii)

Solution 2(iii)

Solution 2(iv)

Solution 2(v)

Solution 2(vi)

Solution 2(vii)

Solution 2(viii)

Solution 3(i)
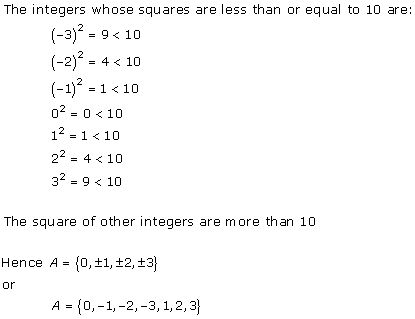
Solution 3(ii)
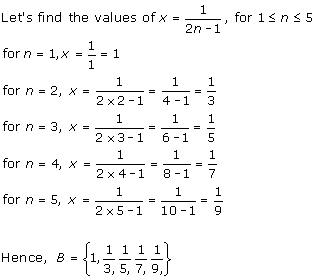
Solution 3(iii)
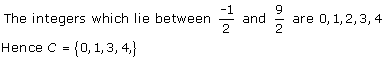
Solution 3(iv)
Solution 3(v)
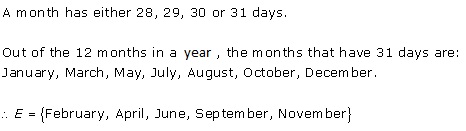
Solution 3(vi)
Solution 4

Solution 5

Solution 6
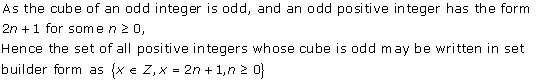
Solution 7

Sets Exercise Ex. 1.3
Solution 1

Solution 2

Solution 3

Solution 4

Solution 5
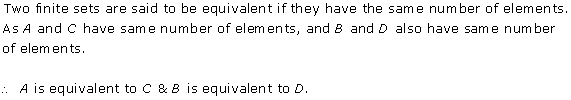
Solution 6

Solution 7

Solution 8

Solution 9
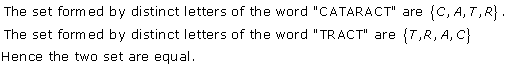
Sets Exercise Ex. 1.4
Solution 1

Solution 2

Solution 3

Solution 4(i)

Solution 4(ii)
Solution 4(iii)
Solution 4(iv)

Solution 4(v)
Solution 4(vi)

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10

Solution 11

Solution 12

Solution 13
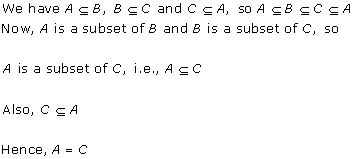
Solution 14
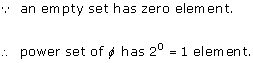
Solution 15

Solution 16

Sets Exercise Ex. 1.5
Solution 1

Solution 2(i)
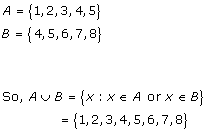
Solution 2(ii)
Solution 2(iii)
Solution 2(iv)
Solution 2(v)
Solution 2(vi)
Solution 2(vii)
Solution 2(viii)

Solution 2(ix)

Solution 2(x)

Solution 3(i)
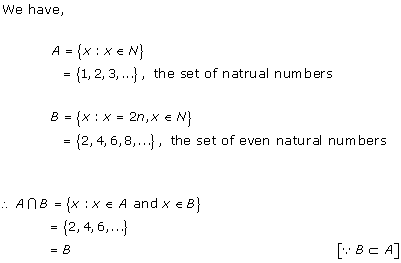
Solution 3(ii)

Solution 3(iii)

Solution 3(iv)
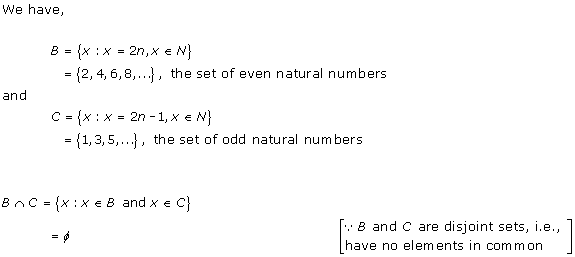
Solution 3(v)
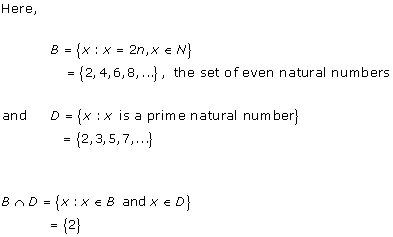
Solution 3(vi)

Solution 4

Solution 5

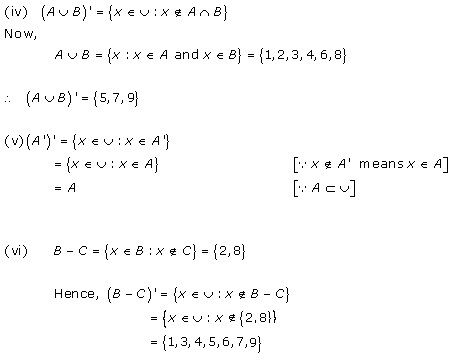
Solution 6

Sets Exercise Ex. 1.8
Solution 1
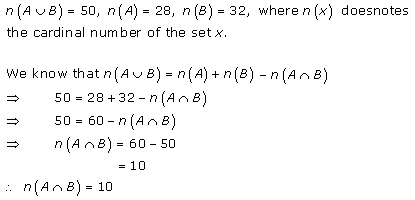
Solution 2
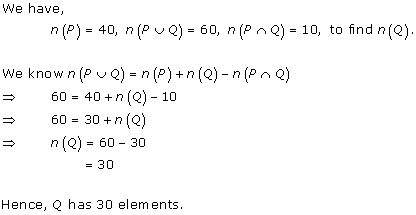
Solution 3

Solution 4

Solution 5(i)
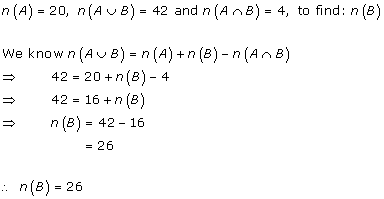
Solution 5(ii)

Solution 5(iii)

Solution 6

Solution 7

Solution 8

Solution 9


Solution 10

Solution 11

Solution 12



Solution 13

Solution 14

Solution 15

Sets Exercise Ex. 1VSAQ
Solution 1
Let A be a set. Then collection or family of all subsets of A is called the power set of A and is denoted by P(A).
A set having n elements has 2n subsets. Therefore, if A is a finite set having n elements, then P(A) has 2n elements.
Solution 2
If A is the void set Φ, then P(A) has just one element Φ i.e. P(Φ) ={Φ}.
Solution 3

Solution 4
![]()

The minimum number of elements that![]() can have is 6.
can have is 6.
Solution 5


Solution 6

Solution 7
![]()

The maximum number of elements that![]() can have is 11.
can have is 11.
Solution 8
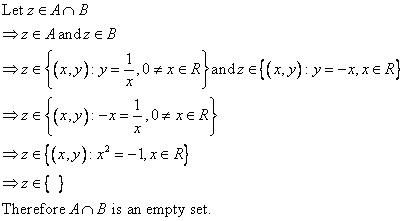
Solution 9

Solution 10

Solution 11


