Class 11-commerce RD SHARMA Solutions Maths Chapter 33: Probability
Probability Exercise Ex. 33.1
Solution 1

Solution 2

Solution 3

Solution 4

Solution 5

Solution 6
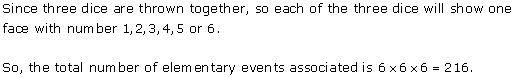
Solution 7
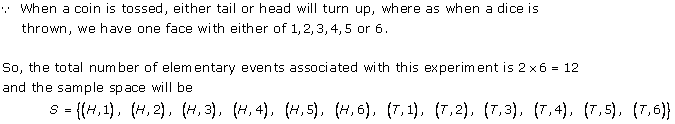
Solution 8
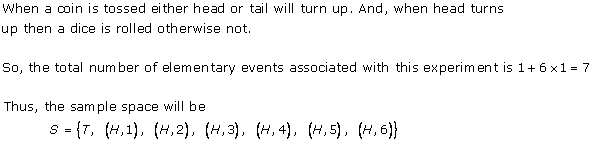
Solution 9

Solution 10
In this experiment, a coin is tossed and if the outcome is tail then a die is tossed once.
Otherwise, the coin is tossed again.
The possible outcome for coin is either head or tail.
The possible outcome for die is 1,2,3,4,5,6.
If the outcome for the coin is tail then sample space is S1={(T,1),(T,2),(T,3),(T,4),(T,5),(T,6)}
If the outcome is head then the sample space is S2={(H,H),(H,T)}
Therefore the required sample space is S={(T,1),(T,2),(T,3),(T,4),(T,5),(T,6),(H,H),(H,T)}
Solution 11

Solution 12

Solution 13
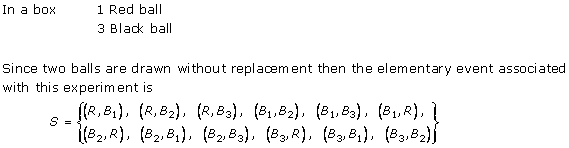
Solution 14
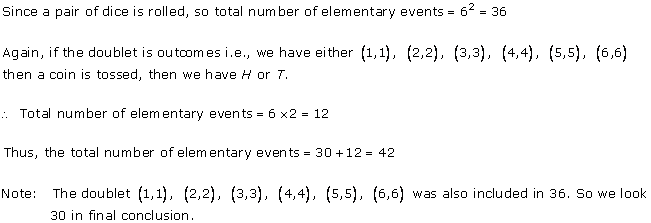
Solution 15

Solution 16

Solution 17
In a random sampling, three items are selected so it could be any of the following:
a) All defective or
b) All non-defective or
c) Combination of defective and non defective.
Sample space associated with this experiment is
S={DDD, NDN, DND, DNN, NDD, DDN, NND, NNN}
Solution 18

Solution 19
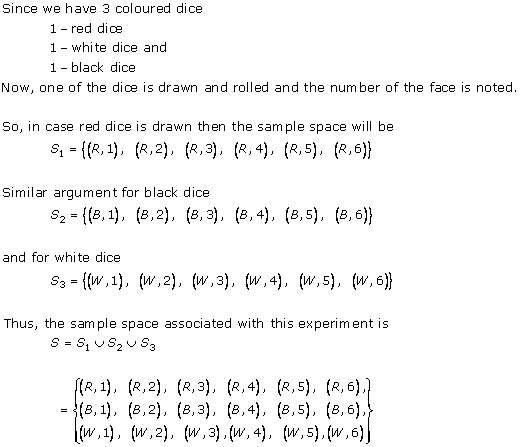
Solution 20
Solution 21

Solution 22

Solution 23

Solution 24
In this experiment, a die is rolled. If the outcome is 6 then experiment is over. Otherwise, die will be rolled again and again.
Probability Exercise Ex. 33.2
Solution 1

Solution 2
Solution 3
Solution 4
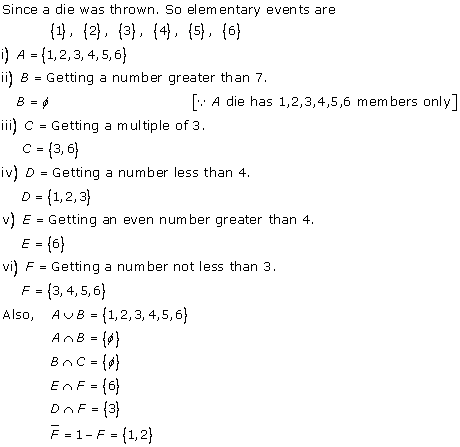
Solution 5
Solution 6
Solution 7
Solution 8
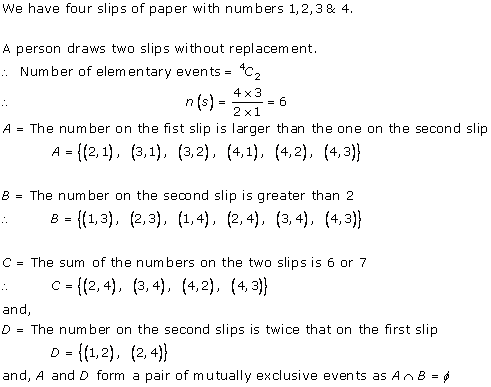
Solution 9
Probability Exercise Ex. 33.3
Solution 1

Solution 2

Solution 3
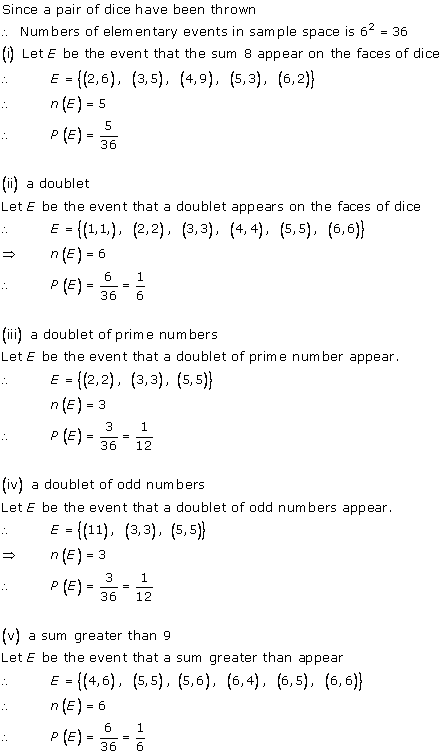

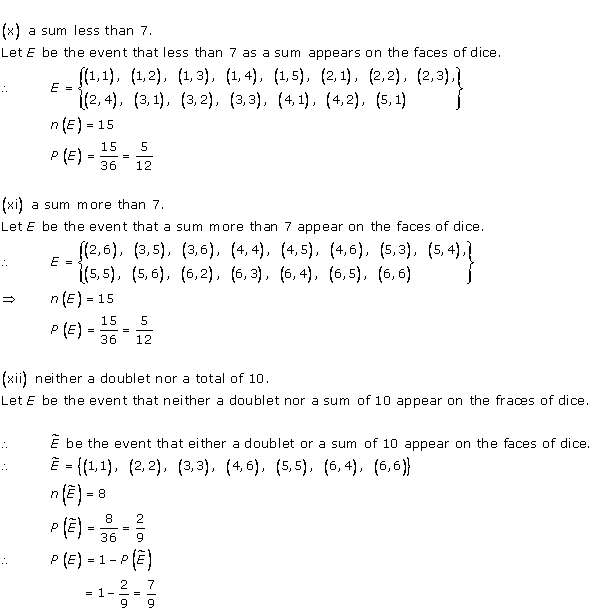
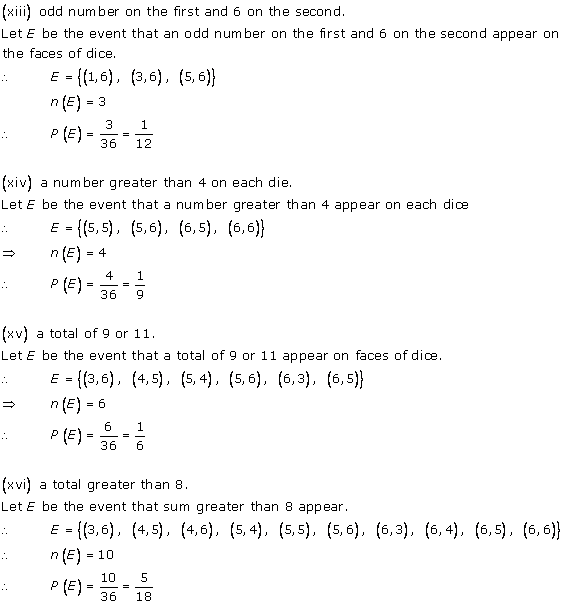
Solution 4

Solution 5

Solution 6

Solution 7

Solution 9

Solution 10

Solution 11



Solution 12

Solution 13

Solution 14

Solution 15
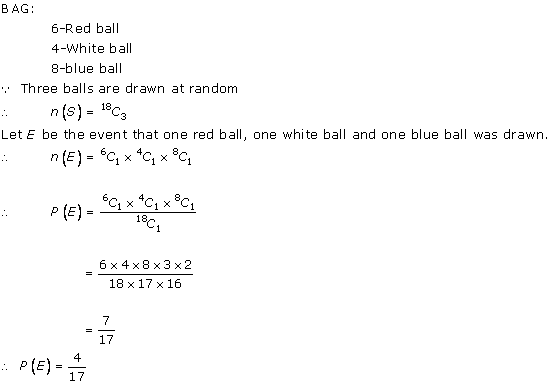
Solution 16
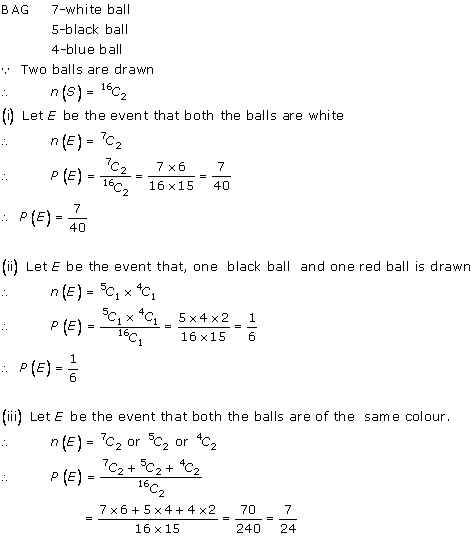
Solution 17
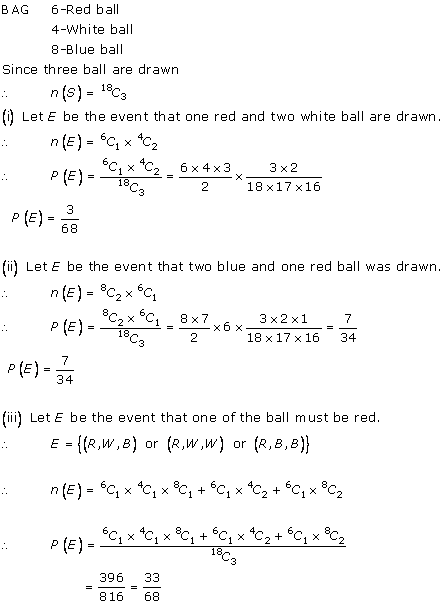
Solution 18
Solution 19

Solution 20
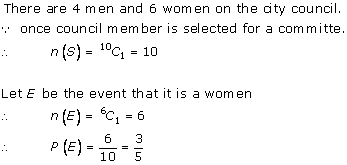
Solution 21
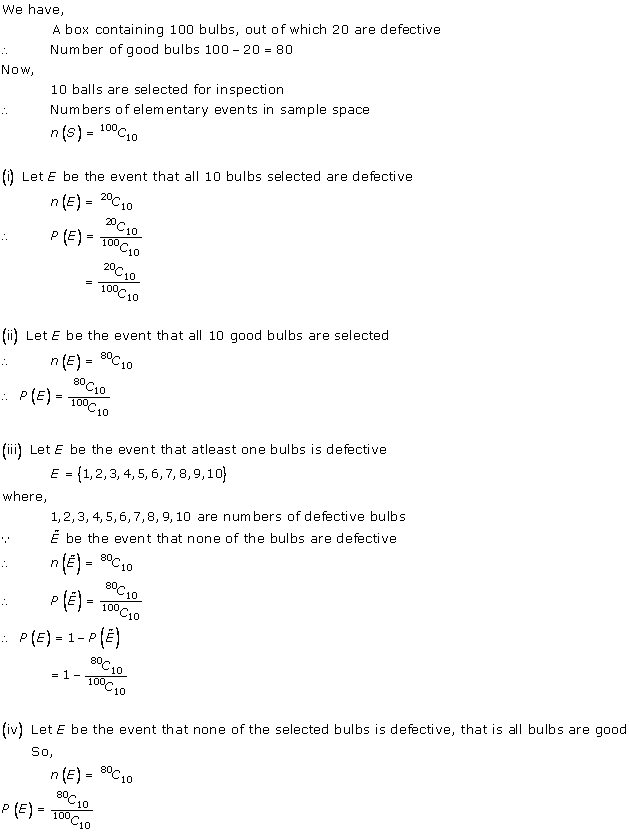
Solution 22
Solution 23

Solution 24

Solution 25

Solution 26
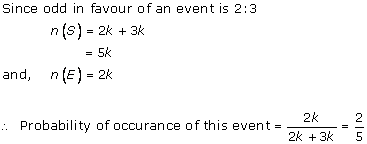
Solution 27

Solution 28

Solution 29
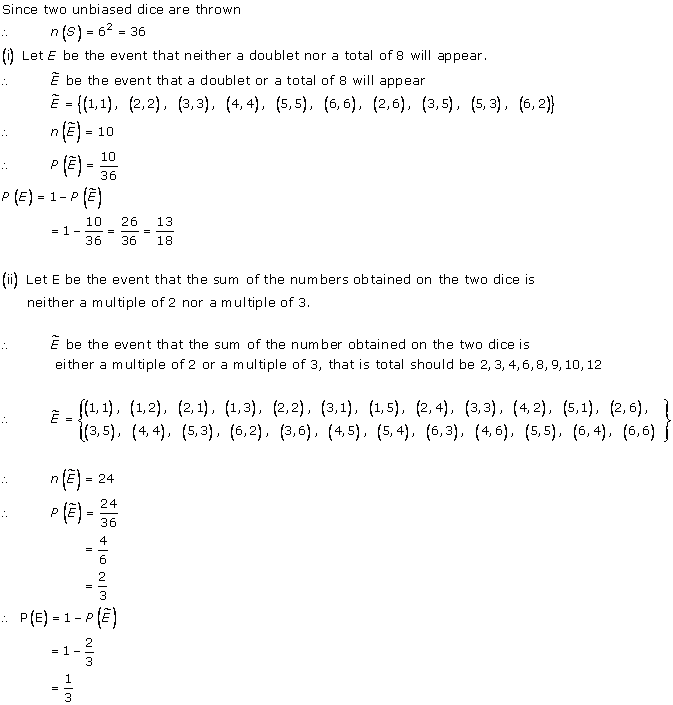
Solution 30
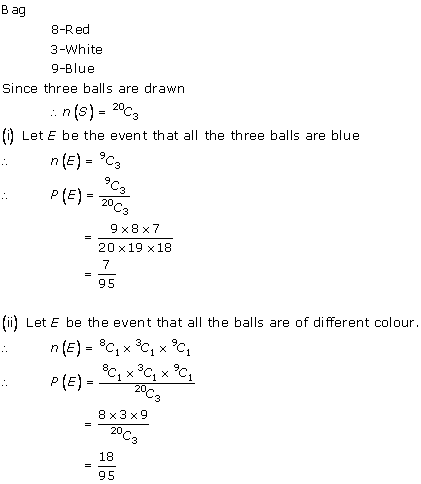
Solution 31

Solution 32

Solution 33

Solution 34


Solution 35
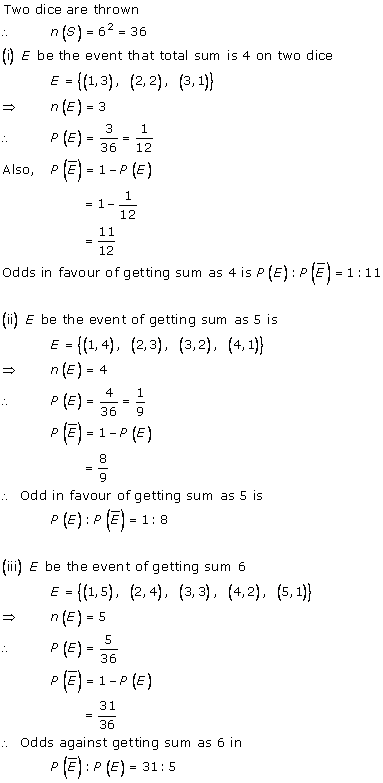
Solution 36

Solution 37
Solution 38

Solution 39
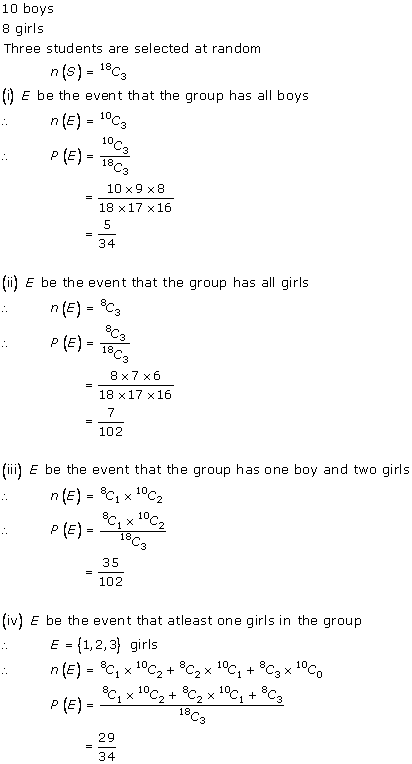

Solution 40

Solution 41

Solution 42
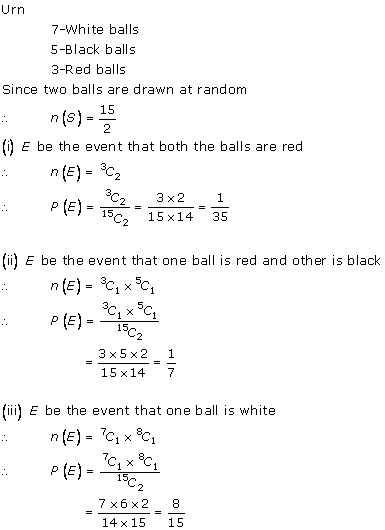
Solution 43
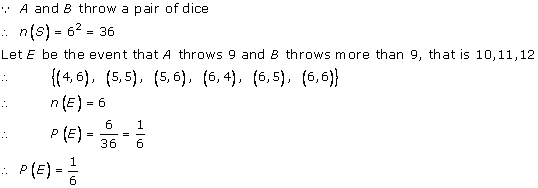
Solution 44

Solution 45

Solution 8
Probability Exercise Ex. 33.4
Solution 1(a)

Solution 1(b)

Solution 1(c)

Solution 2

Solution 3
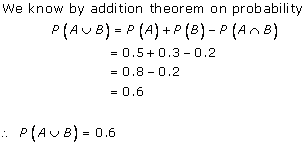
Solution 4
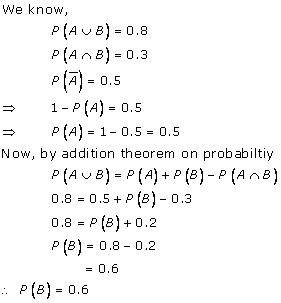
Solution 5
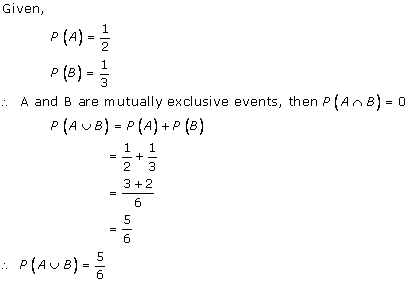
Solution 6
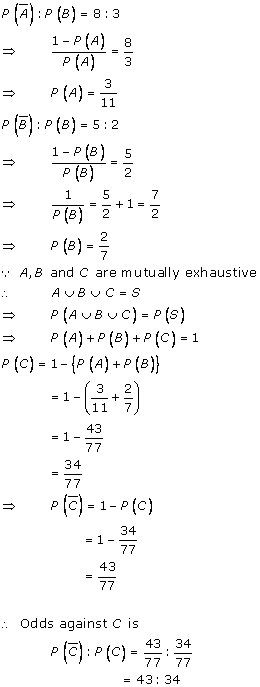
Solution 7
Solution 8

Solution 9
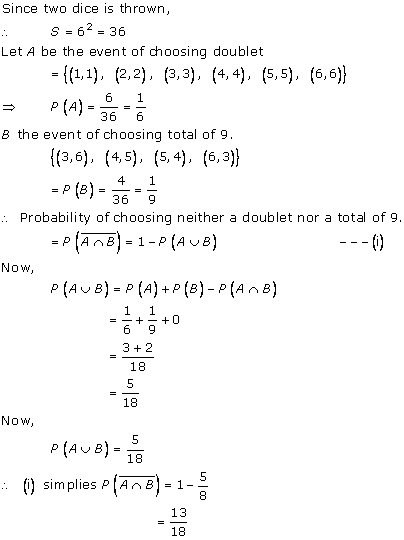
Solution 10
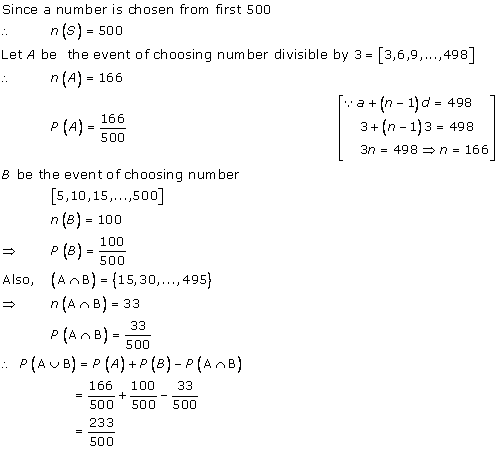
Solution 11

Solution 12

Solution 13

Solution 14
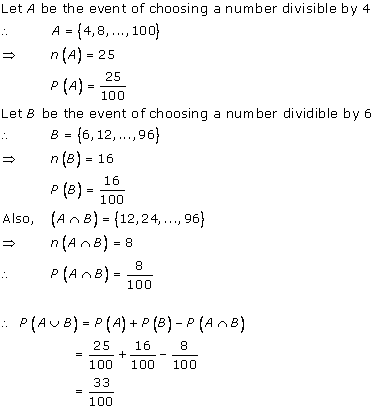
Solution 15

Solution 16

Solution 17

Solution 18
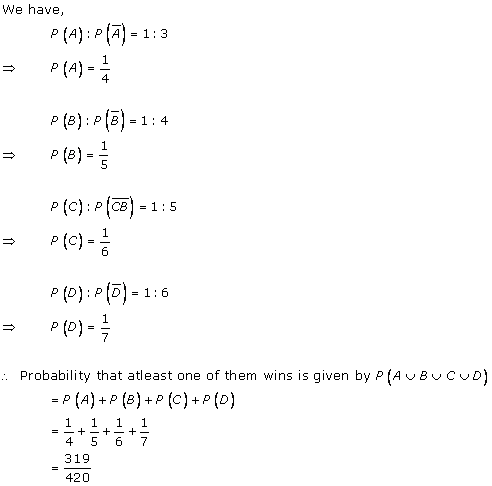
Solution 19
Solution 20
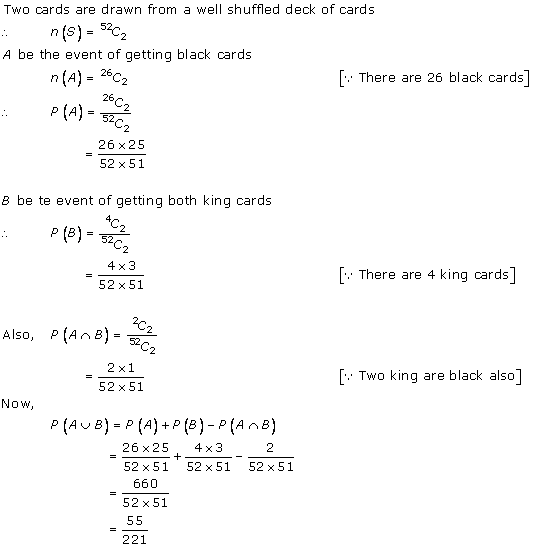
Solution 21
Solution 22
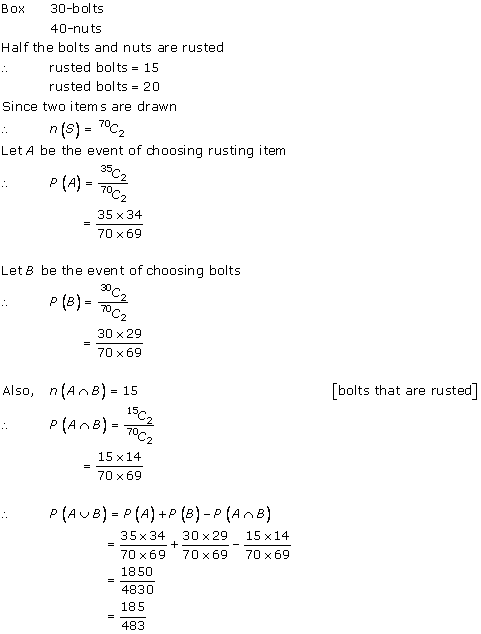
Solution 23

Solution 24
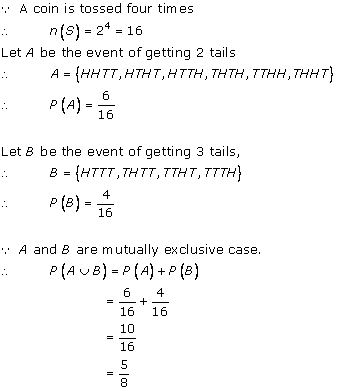
Solution 25
Solution 26
Solution 27
Solution 28
Probability Exercise Ex. 33VSAQ
Solution 1
Solution 2

Solution 3

Solution 4
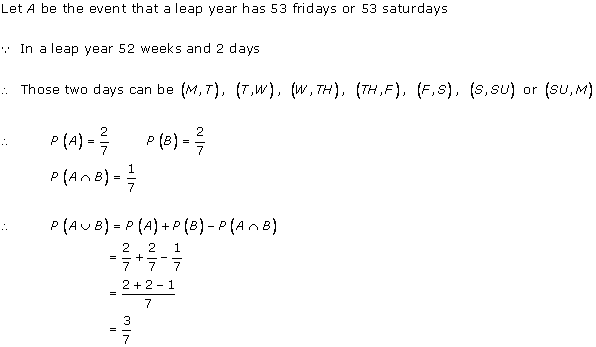
Solution 5

Solution 6

Solution 7

Solution 8
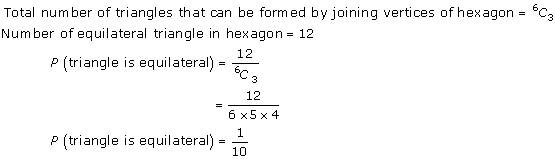
Solution 9

Solution 10