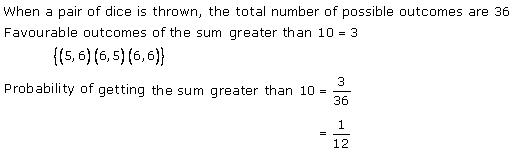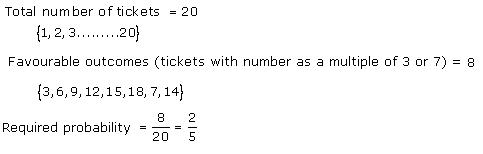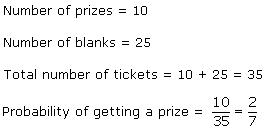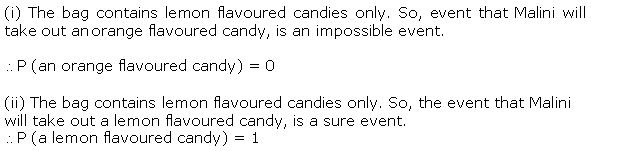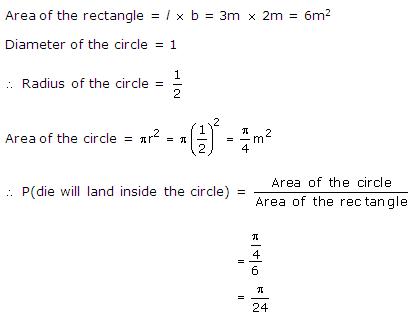Class 10 RD SHARMA Solutions Maths Chapter 16 - Probability
Probability Exercise Ex. 16.1
Solution 1

Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
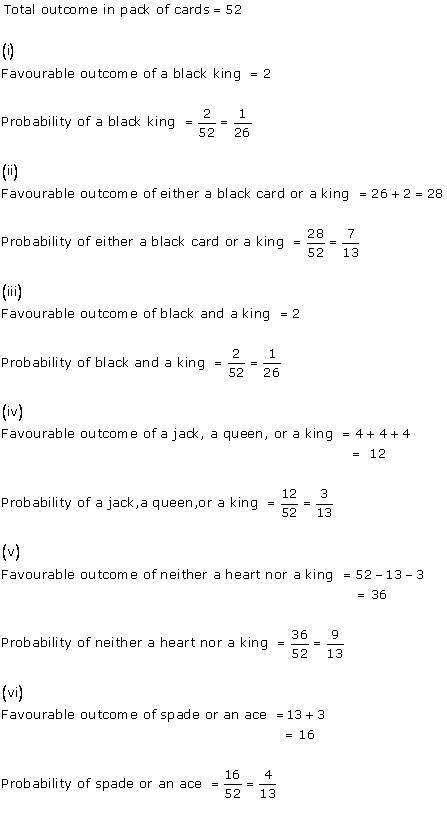
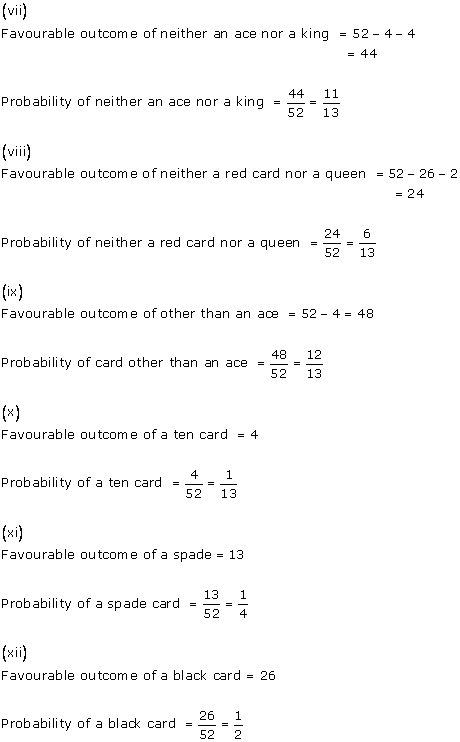

Solution 6(xix)

Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
Solution 13
Solution 14
Solution 15

Solution 16
Solution 17
Solution 18
Solution 19(i)
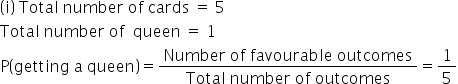
Solution 19(ii)

Solution 20
Solution 21
Solution 22

Solution 23
A coin has only two options-head and tail and both are equally likely events i.e. the probability of occurrence of both is same. Hence, a coin is a fair option to decide which team will choose ends in the game.
Solution 24

Solution 25

Solution 26
Solution 27
Solution 28
Solution 29
Solution 30
Solution 31
Solution 32
Solution 33
Solution 34
Solution 35
Solution 36
Solution 37
Solution 38
Solution 39

Solution 40
Solution 41
(i) 1
(ii) 0
(iii) 0 and 1
(iv) equal
(v) 1
(vi) 1
Solution 42
Solution 43
Solution 44

Solution 45

Solution 46
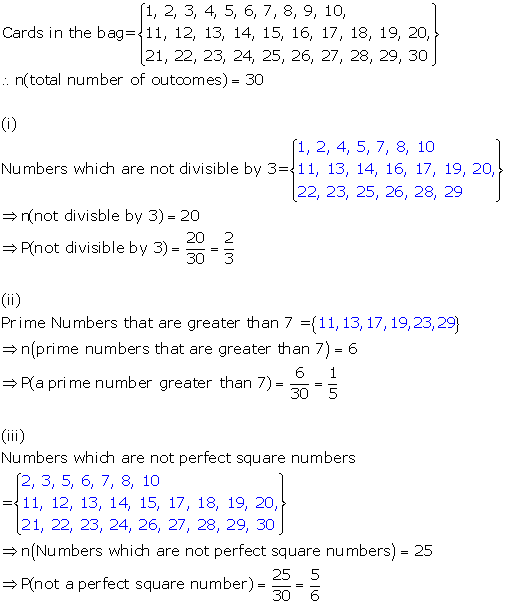
Solution 47
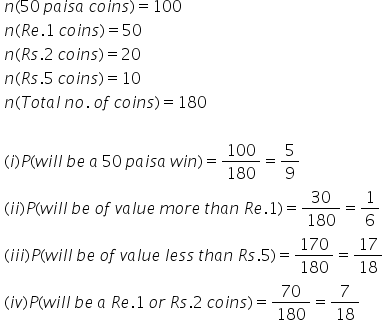
Solution 48

Solution 49

Solution 50


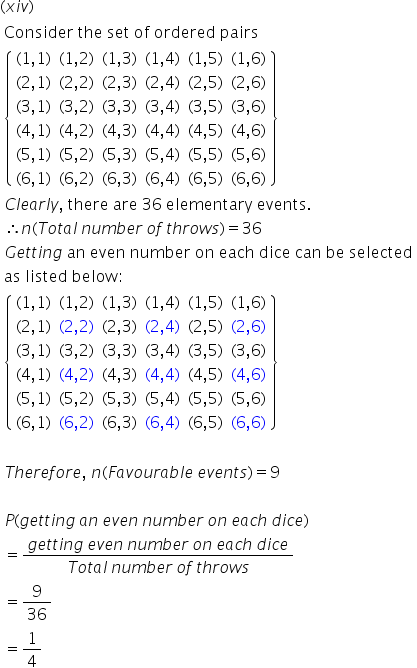

Solution 50(xvi)

Solution 50(xvii)
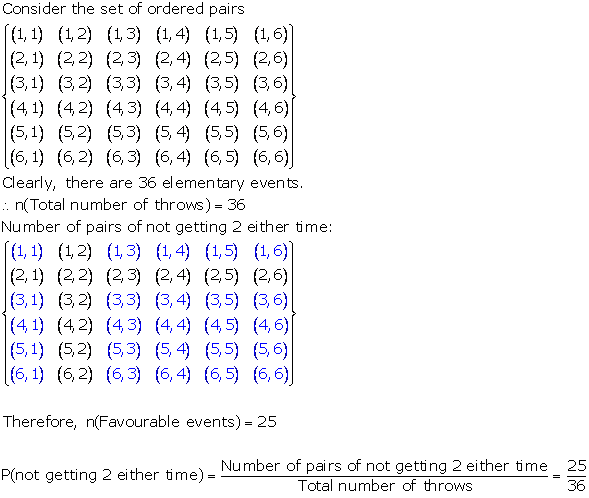
Solution 51
Solution 52
Solution 53

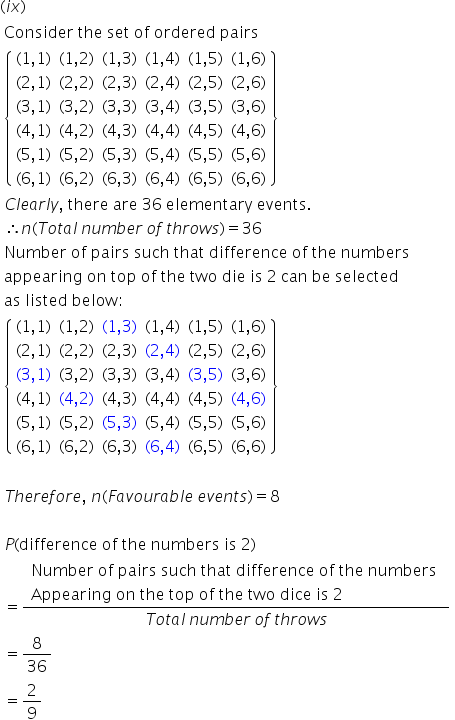
(x)
When a black die and a white die are thrown at the same time, the sample space is given by
S = {(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
(2,1)(2,2),(2,3),(2,4),(2,5),(2,6),
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}
n(S) = 36
Let A be the event that the numbers obtained have a product less than 16.
A = {{(1,1),(1,2),(1,3),(1,4),(1,5),
(1,6),(2,1)(2,2),(2,3),(2,4),(2,5),
(2,6),(3,1),(3,2),(3,3),(3,4),(3,5),
(4,1),(4,2),(4,3), (5,1),(5,2),
(5,3),(6,1),(6,2)}}
n(A) = 25
P(A) =
Solution 54
Solution 55
Solution 56

Solution 57
Solution 58
Solution 59
Solution 60

Solution 61
Solution 62
Solution 63
Solution 64
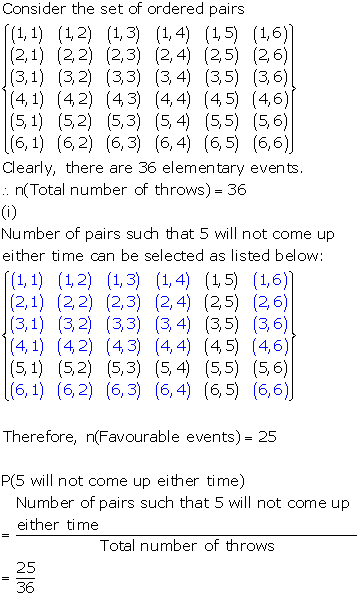
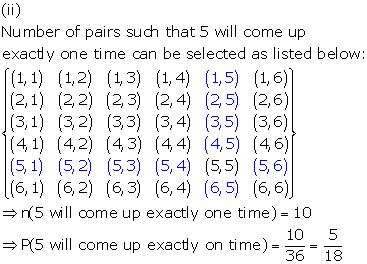
Solution 65

Solution 66

Solution 67

Solution 68

Solution 69

Solution 70
![]()

Solution 71

Solution 72
Solution 3(i)
Sample space when three coins are tossed together is
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
n(S) = 8
Let A be the event ofgetting exactly two heads.
A = {HHT, THH, HHT}
n (A) = 3
P(A)
= ![]()
Solution 3(ii)
Sample space when three coins are tossed together is
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
n(S) = 8
Let A be the event of getting at most two heads.
A = {TTT, HTT, THT, TTH, HHT, THH, HHT}
n (A) = 7
P(A)
= ![]()
Solution 3(iii)
Sample space when three coins are tossed together is
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
n(S) = 8
Let A be the event of getting at least one head and one tail.
A = {HHT, HTH, THH, HTT, THT, TTH }
n (A) = 6
P(A)
= ![]()
Solution 3(iv)
Sample space when three coins are tossed together is
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
n(S) = 8
Let A be the event ofgetting no tails.
A = {HHH}
n (A) = 1
P(A)
= ![]()
Probability Exercise Ex. 16.2
Solution 1
Solution 2
Solution 3
Assume first circle to be the circle with the smallest radius, that is 3. Similarly, second circle to be the circle with radius 7 and third circle to be the circle with radius 9.
Solution 4
Solution 5
Solution 6
Probability Exercise 16.35
Solution 1
n(E) = total numbers
= 9
n(0) = odd numbers {1, 3, 5, 7, 9}
= 5

So, the correct option is (b).
Solution 2
n(E) = 9
n(4) = no. is even {2, 4, 6, 8}
= 4

So, the correct option is (a).
Probability Exercise 16.36
Solution 3
n(E) = 9
n(A) = no. is multiple of 3 {3, 6, 9}
= 3
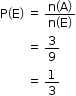
So, the correct option is (a).
Solution 4
3 coins are tossed simultaneously.
Hence sample space = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
Event (E) = at least two Heads
= {HHH, HHT, HTH, THH}
n(s) = 8
n(E) = 4
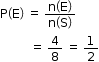
So, the correct option is (c).
Solution 5
sample space (s) = {1, 2, 3, 4, 5, 6}
n(s) = 6
Event (E) = getting a multiple of 3
= {3, 6}
n(E) = 2
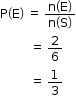
So, the correct option is (b).
Solution 6

Solution 7

Solution 8

Solution 9
Sample space (S) = {1, 2, 3, 4, 5, 6}
n(S) = 6
Event (E) = getting number greater than 2
= {3, 4, 5, 6}
n(E) = 4
![]()
So, the correct option is (c).
Solution 10
n(S) = 52
no. of ace in a pack of 52 cards = 4
n(E) = 4

So, the correct option is (b).
Solution 11
n(S) = 25
Event (E) = prime numbers between 1 to 25
= {2, 3, 5, 7, 11, 13, 17, 19, 23}
n(E) = 9
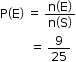
Note: The answer does not match the options in the question.
Solution 12
We know probability P(E) of an event lies between 0 < P(E) < 1 ......(1)
(a), (c), (d) satisfies the (1) but (b) is a negative number. It can't be the probability of an event.
So, the correct option is (b).
Solution 13
We know
P(E) + P(not E) = 1
given P(E) = 0.05
so P(not E) = 1 - 0.05
= 0.95
So, the correct option is (d).
Solution 14
We know 0 < P(E) < 1
(a), (b), (c) fullfill the condition. But (d) doesn't
Hence (d) is correct option.
So, the correct option is (d).
Solution 15
An event that is certain to occur is called Certain event.
Probability of certain event is 1.
Ex: If it is Monday, the probability that tomorrow is Tuesday is certain and therefore probability is 1.
So, the correct option is (b).
Probability Exercise 16.37
Solution 16
Events that are not possible are impossible event.
Probability of impossible event is 0.
So, the correct option is (a).
Solution 17

Solution 18

Solution 19
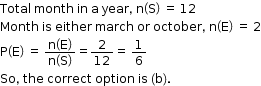
Solution 20

Solution 21

Solution 22

Solution 23

Solution 24

Solution 25

Solution 26

Solution 27

Probability Exercise 16.38
Solution 28

Solution 29
Sample space (s) = {-3, -2, -1, 0, 1, 2, 3}
n(s) = 7
Event (E) = |x| < 2
= {-1, 0, 1}
n(E) = 3
![]()
So, the correct option is (c).
Solution 30

Solution 31
There are 365 days in a non-leap year.
52 complete weeks and 1 spare day.
so This day can be any out of 7 day of week.
Hence n(s) = 7
Now, year already have 52 Sundays. so for a total of 53 Sundays in a calendar year, this spare day must be a Sunday.
Hence n(E) = 1
![]()
So, the correct option is (d).
Solution 32
We know on throwing a pair of die there are a total of 36 possible outcomes.
n(S) = sum is a perfect square
= {(1, 3), (2, 2), (3, 1), (3, 6), (4, 5), (5, 4), (6, 3)}
n(E) = 7
![]()
So, the correct option is (b).
Solution 33
There are 365 days in a non-leap year.
52 complete weeks and 1 spare day.
So this day can be any out of 7 day of a week.
Hence n(s) = 7
Now, a non-leap year already has 52 Sundays. So for a total of 53 Sundays in a calendar year, this spare day must be a Sunday.
Hence n(E) = 1
![]()
So, the correct option is (b).
Solution 34

Solution 35

Solution 36

Solution 37

Solution 38

Probability Exercise 16.39
Solution 39
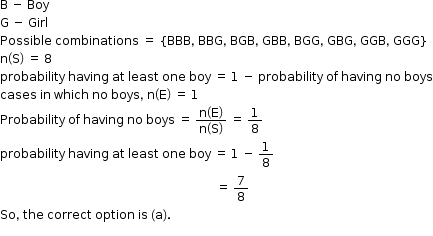
Solution 40