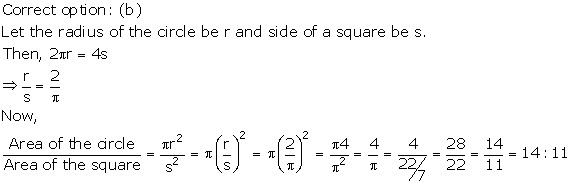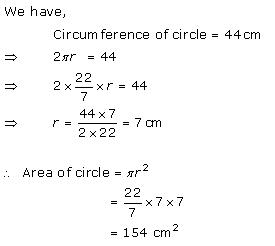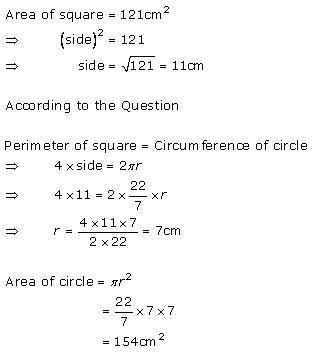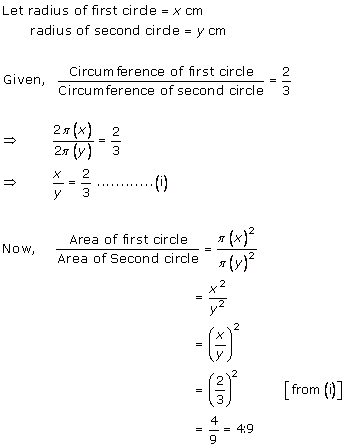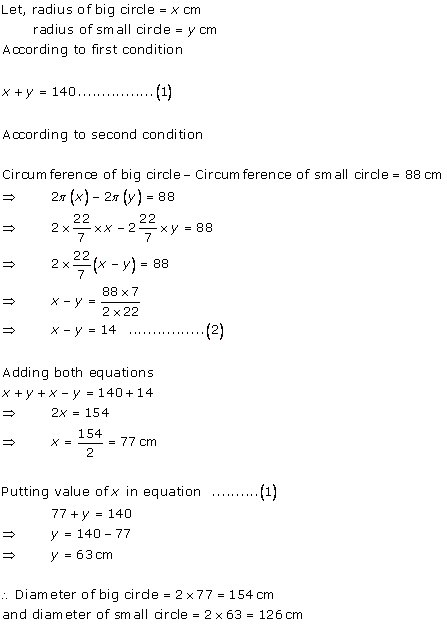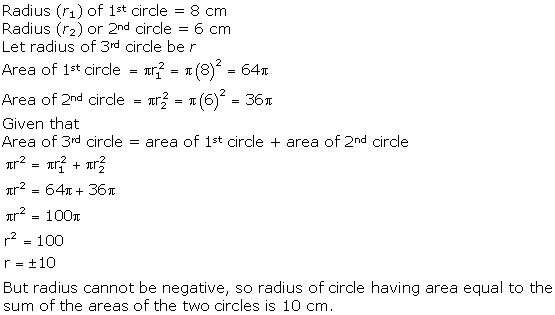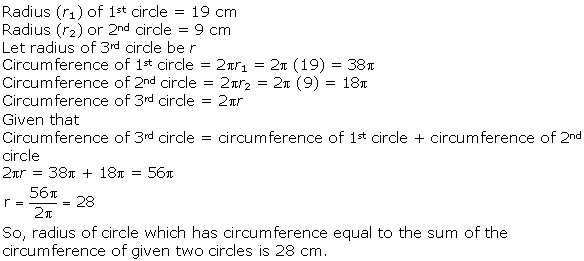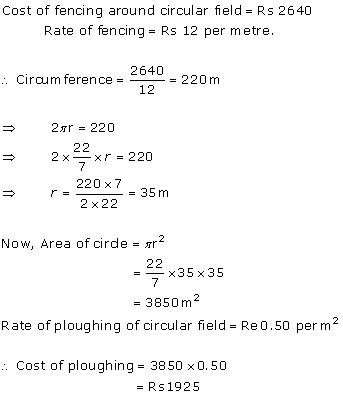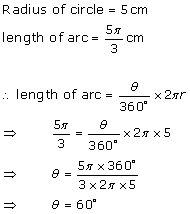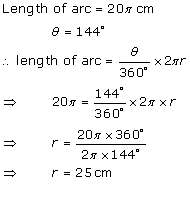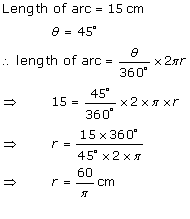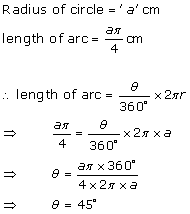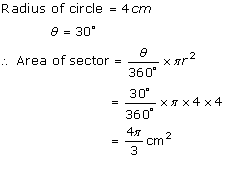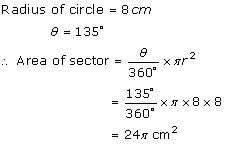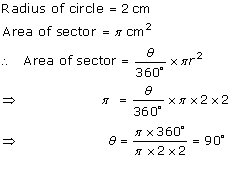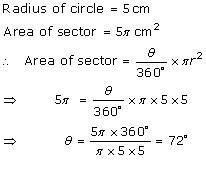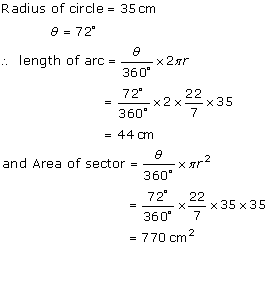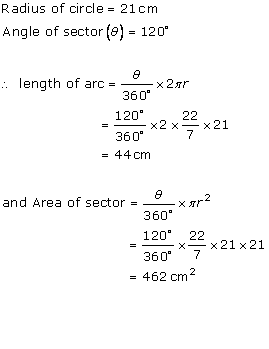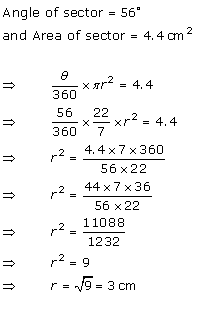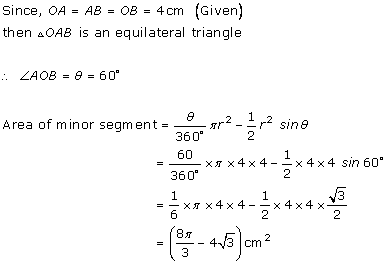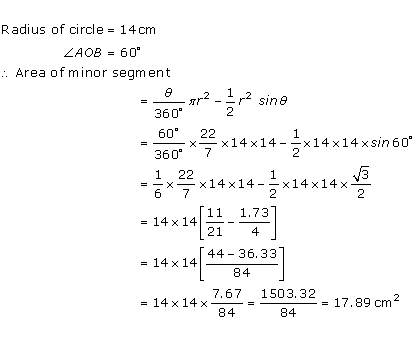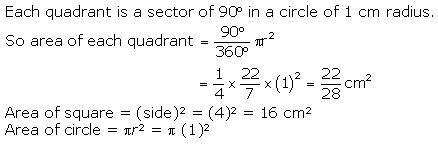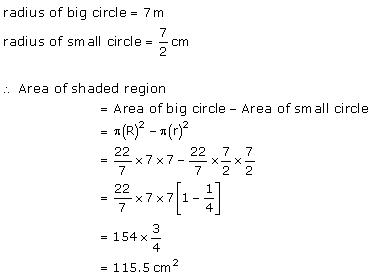Class 10 RD SHARMA Solutions Maths Chapter 13 - Areas Related to Circles
Areas Related to Circles Exercise Ex. 13.1
Solution 1
Solution 2
Solution 3
Solution 4
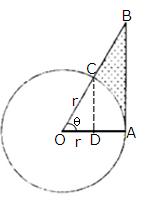
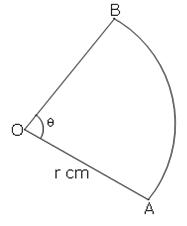
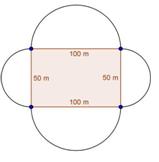
Solution 5
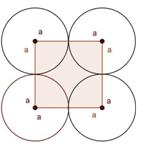
Solution 6
Solution 7
Solution 8
Solution 9
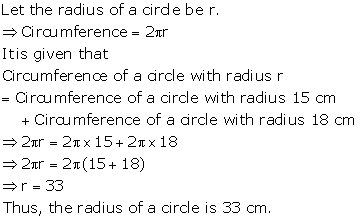
Solution 10
Solution 11
Area of a circle = πr2 = (22/7) × 28 × 28 = 2464 cm2
Solution 12

Solution 13
Solution 14
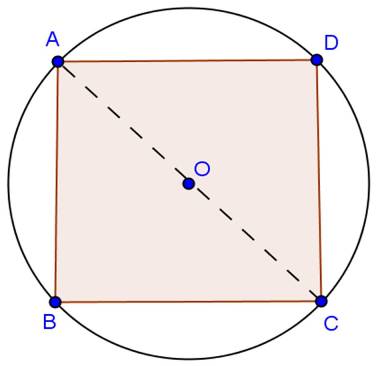
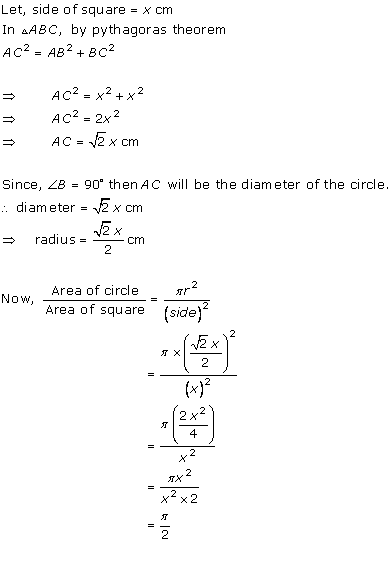
Solution 15
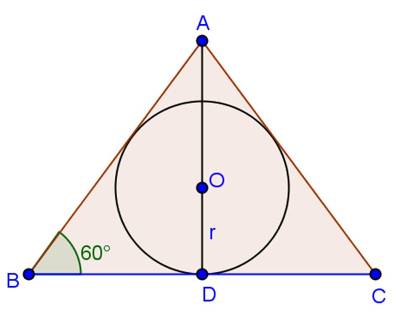
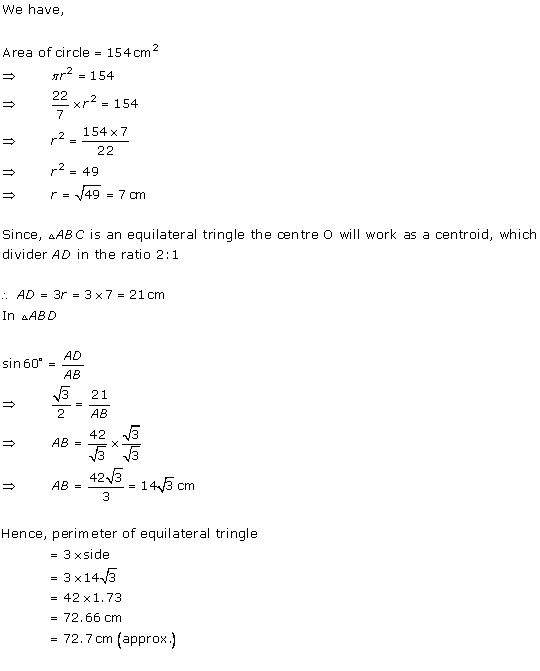
Solution 16
Solution 17
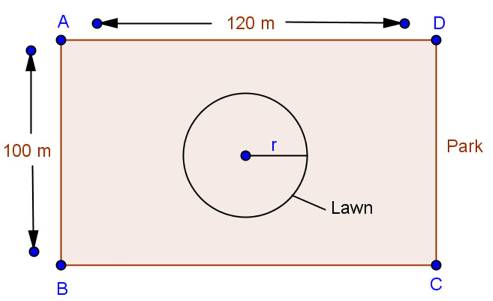

Solution 18

Solution 19
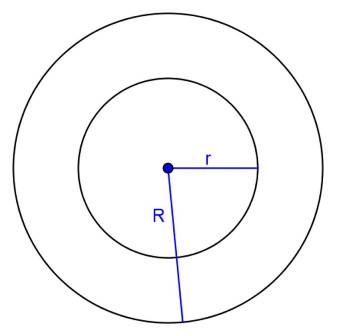
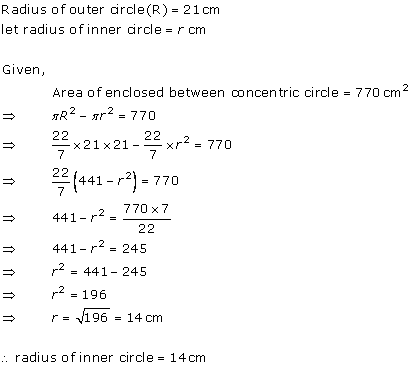
Solution 20

Solution 21
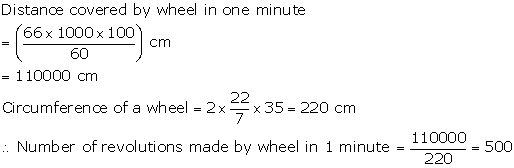
Solution 22

Solution 23

Solution 24
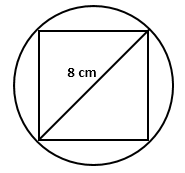
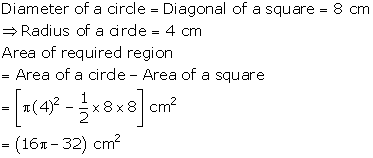
Solution 25
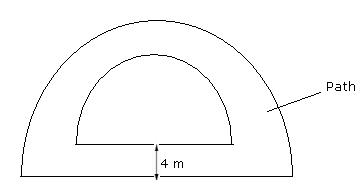
Solution 26
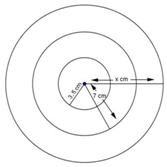
Solution 27
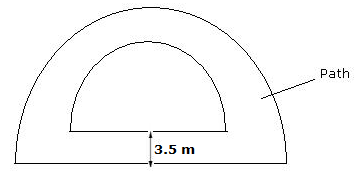

Solution 28

Solution 29
Solution 30

Solution 31
Areas Related to Circles Exercise Ex. 13.2
Solution 1
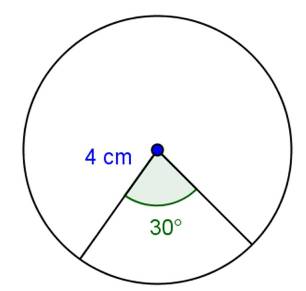
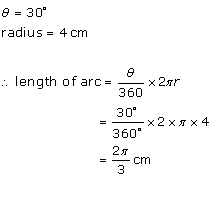
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
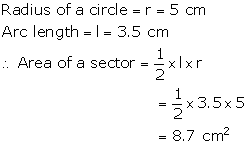
Solution 11
Solution 12
Solution 13
Solution 14
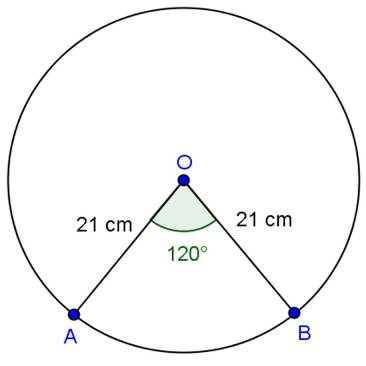
Solution 15

Solution 16

Solution 17
Solution 18
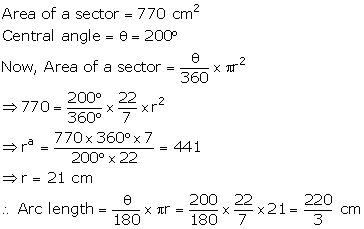
Solution 19

Solution 20
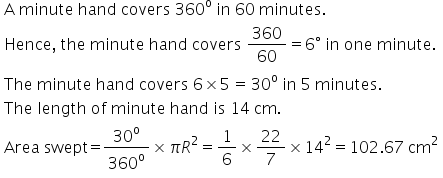
*Answer does not match with textbook answer.
Solution 21
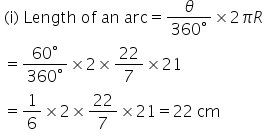
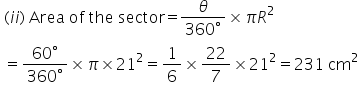
Solution 22
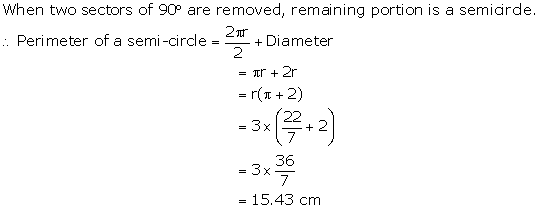
*Note: Answer given in the book is incorrect.
Solution 23
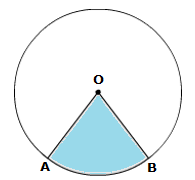
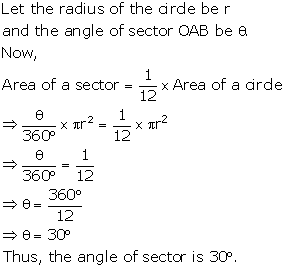
Solution 24
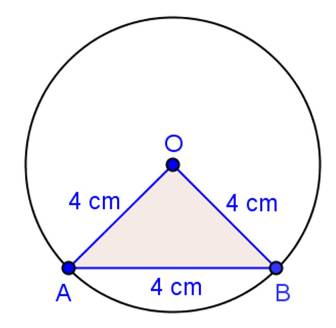
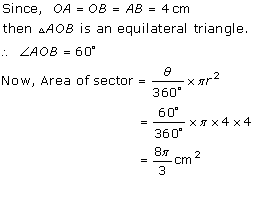
Solution 25
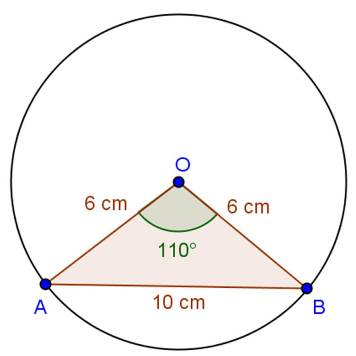
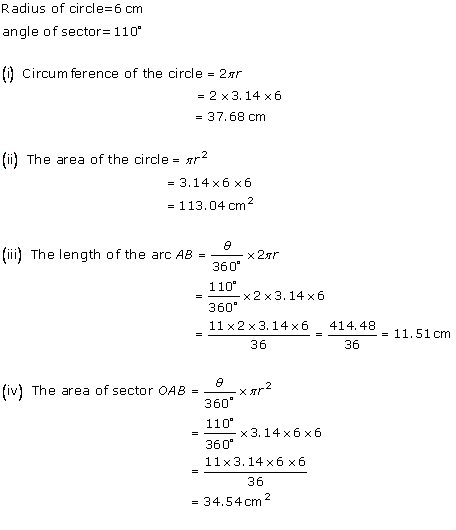
Solution 26
Solution 27
Areas Related to Circles Exercise Ex. 13.3
Solution 1
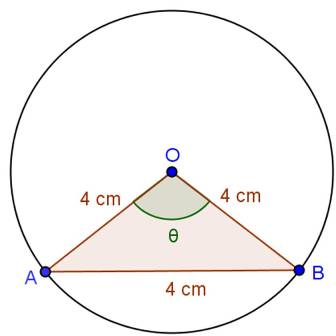
Solution 2
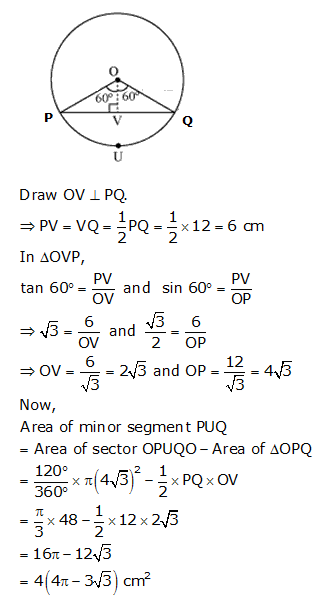
Solution 3
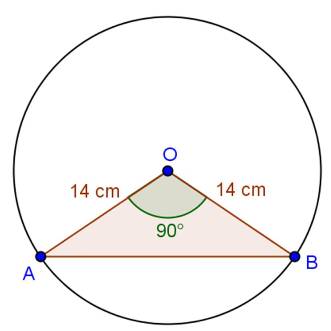
Solution 4
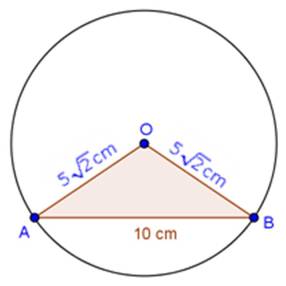
Solution 5
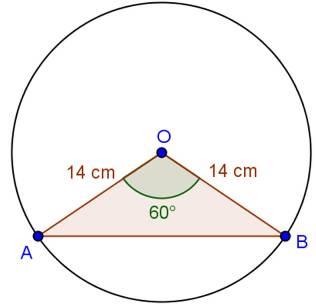
Solution 6
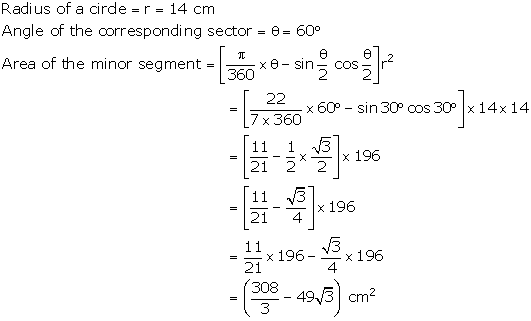
Solution 7
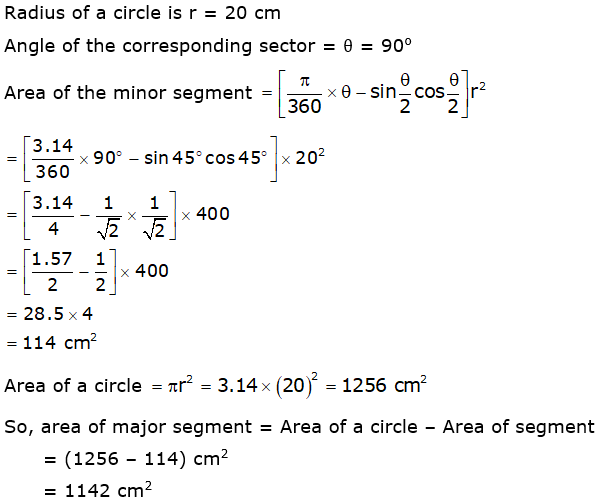
Solution 8

Solution 9
Solution 10
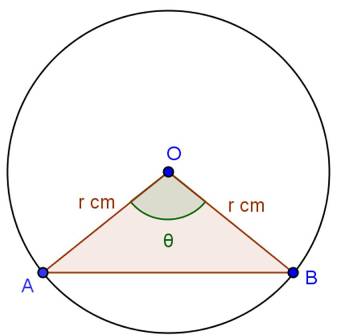
Areas Related to Circles Exercise Ex. 13.4
Solution 1

Solution 2
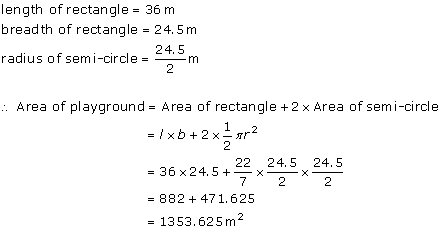
Solution 3
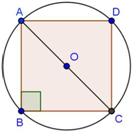
Solution 4

Solution 5
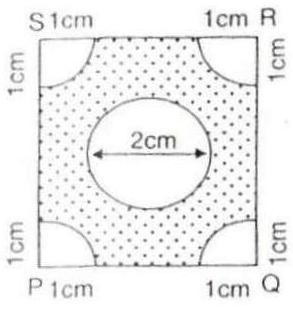
Solution 6

Solution 7
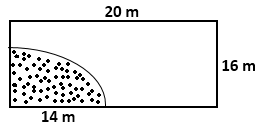

Solution 8
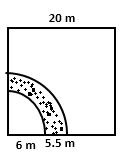

Solution 9

Solution 10
Solution 11
Solution 12
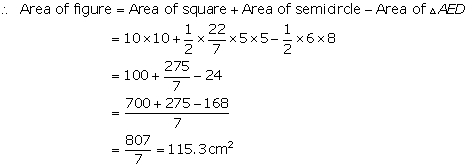
Solution 13

Solution 14

Solution 15

Solution 16
Solution 17
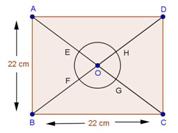
Solution 18
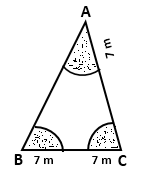

Solution 19
Solution 20

Solution 21
Solution 22

Solution 23

Solution 24
Solution 25
*Answer is not matching with textbook.
Solution 26
Solution 27

Solution 28
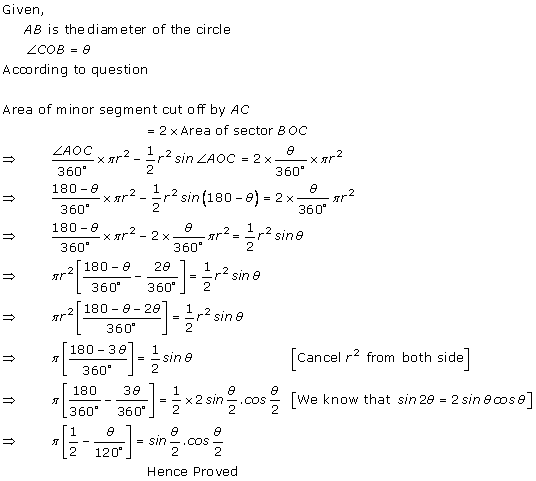
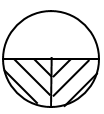
Consider the following figure:
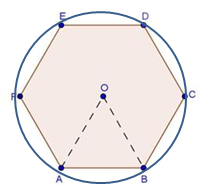
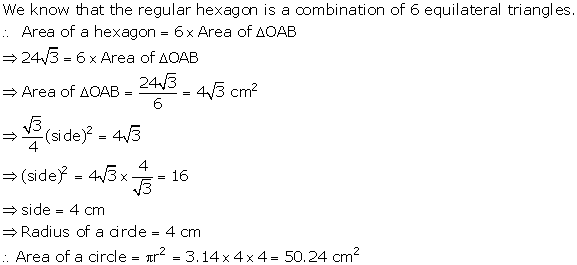
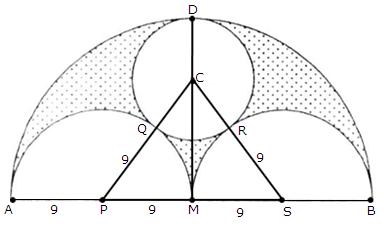
Solution 29
(i)
According to the figure in the question, there are 6 triangles.
Area of one triangle is 9 cm2.
Area of hexagon = 6 × 9 = 54 cm2
(ii)
Area of the equilateral triangle = 9 cm2
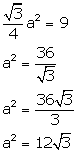
Area of the circle in which the hexagon is inscribed
=
![]()
=
![]()
=
![]()
= 65.26 cm2
NOTE: Answer not matching with back answer.
Solution 30
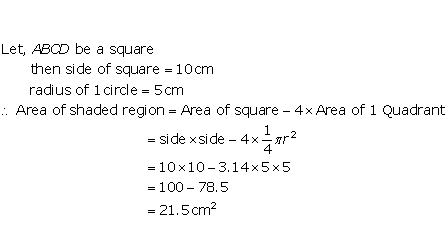
Solution 31
Solution 32

Solution 33

Solution 34

Solution 35
Solution 36

Solution 37

Solution 38

Solution 39
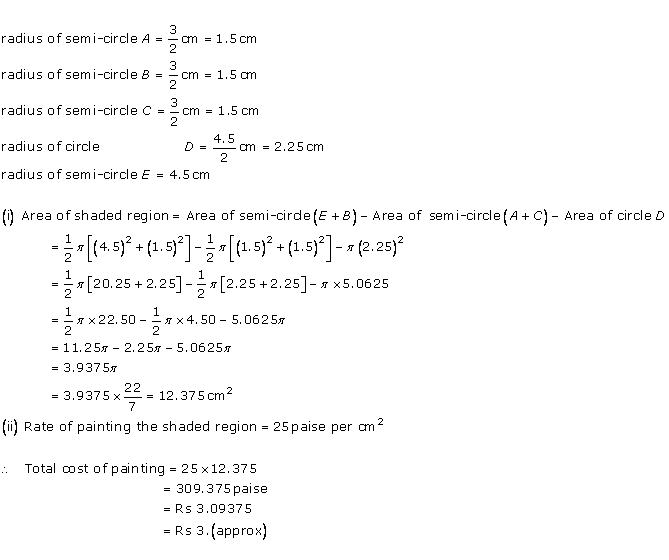
Solution 40
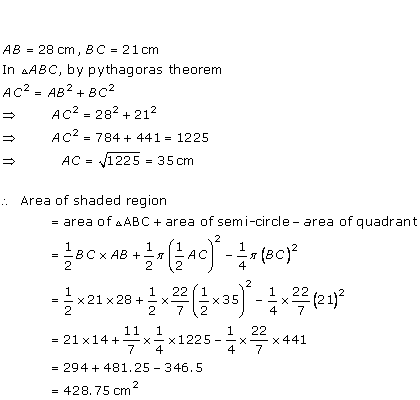
Solution 41
Solution 42
Solution 43
Solution 44

Solution 45
Solution 46

Solution 47
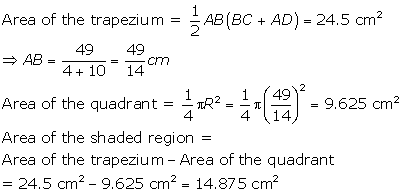
Solution 48
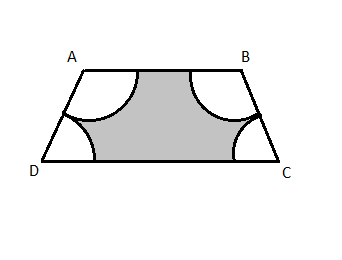
Since the data given in the question seems incomplete and inconsistent with the figure, we make the following assumptions to solve it:
1. ABCD a symmetric trapezium with AD = BC
2. AD = BC = 14 cm (the distance between AB and CD is not 14 cm)
Draw perpendiculars to CD from A and B to divide the trapezium into one rectangle and two congruent right angled triangles.
The base of the right angled triangle=(CD - AB) ÷ 2
=(32 - 18) ÷ 2=7 cm
cos∠D = base ÷ hypotenuse = 7 ÷ 14 =1/2
m∠D = 60°
Hence, m∠A = 120°

*Answer is not matching with textbook answer.
Solution 49

Solution 50

Solution 51


Solution 52
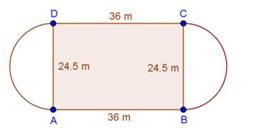
According to the question,
Side of a square is 28 cm.
Radius of a circle is 14 cm.
Required area = Area of the square + Area of the two circles - Area of two quadrants …(i)
Area of the square = 282 = 784 cm2
Area of the two circles = 2πr2
= ![]()
= 1232 cm2
Area of two quadrants = ![]()
= ![]()
= 308 cm2
Required area = 784 + 1232 - 308 = 1708 cm2
NOTE: Answer not matching with back answer.
Solution 53
According to the question,
For a cylindrical tank
d = 2 m, r = 1 m, h = 5 m
Volume of the tank = πr2h
= ![]()
= ![]()
After recycling, this water is used irrigate a park of a hospital with length 25 m and breadth 20 m.
If the tank is filled completely, then
Volume of cuboidal park = Volume of tank
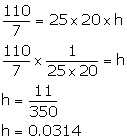
h = 0.0314 m = 3.14 cm = p cm
Solution 54
Join OB.
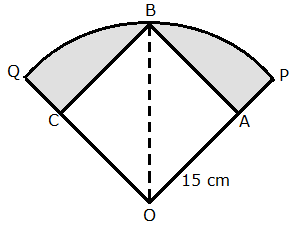
Here, ![]() is a right triangle.
is a right triangle.
By Pythagoras theorem,
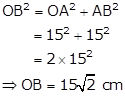
Therefore, radius of the circle (r) ![]()
Area of the square ![]()
Area of the quadrant of a circle ![]()
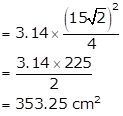
Area of the shaded region = Area of quadrant - Area of square
= 128.25 cm2
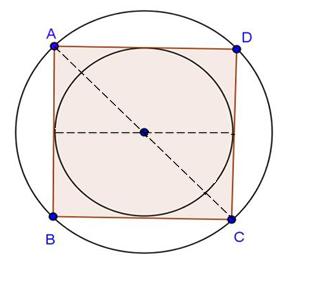
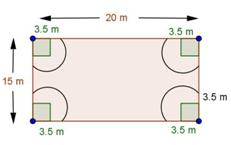
Solution 55
Join AC.
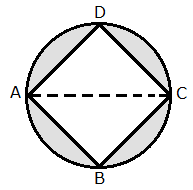
Here, ![]() is a right triangle.
is a right triangle.
By Pythagoras theorem,
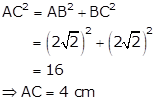
Therefore, diameter of the circle = 4 cm
So, the radius of the circle (r) = 2 cm
Area of the square ![]()
Area of the circle ![]()
Area of the shaded region = Area of the circle - Area of square
= 4.56 cm2
Areas Related to Circles Exercise 13.69
Solution 1
Correct Option :- (D)

Solution 2
According to the question,
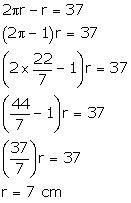
Circumference
of a circle = ![]()
= ![]()
= 44 cm
Solution 3
Correct option (c)

Solution 4
correct option - (c)

Solution 5
correct option - (b)
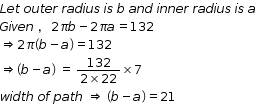
Solution 6
Correct Option: d

Solution 7
Correct Option: (c)
Solution 8
Correct option - (c)

Solution 9
Correct option (c)

Solution 10
Correct Option ( d )
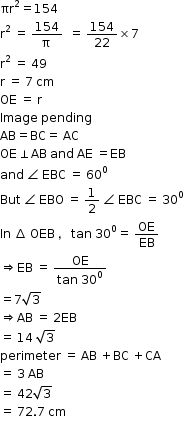
Solution 11
Correct option (a)

Solution 12
Let r be the radius of the circle.
2pr = 88
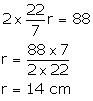
Perimeter of a triangle = 30 cm
Semi-perimeter = 15 cm
Hence,
Area of a triangle = r × s …(r = incircle radius, s =semi perimeter)
= 14 × 15
= 210 cm2
Solution 13
Correct option - (c)

Areas Related to Circles Exercise 13.70
Solution 14

Solution 15

Solution 16

Solution 17

Solution 18

Solution 19

Solution 20

Solution 21

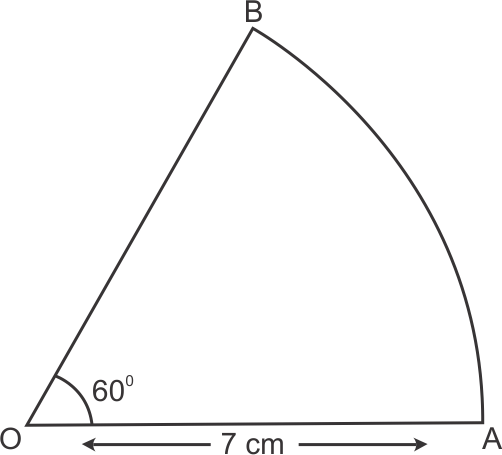
Solution 22

Solution 23

Solution 24
Correct option: (d)
Diameter of circle = side of square
2r = 10
r = 5 cm
Area of circle = πr2 = 25 π cm2

Solution 25
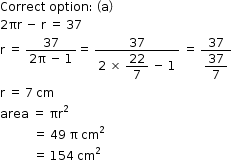
Areas Related to Circles Exercise 13.71
Solution 26
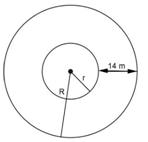
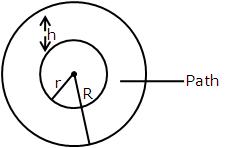
Correct option: (b)
Inner radius = r
outer radius = r + h
area of shaded region = area of outer circle - area of inner circle
= π (r + h)2 - πr2
= π {(r + h)2 - r2 }
= π (r + h - r) (r + h + r)
= π (2r + h) h
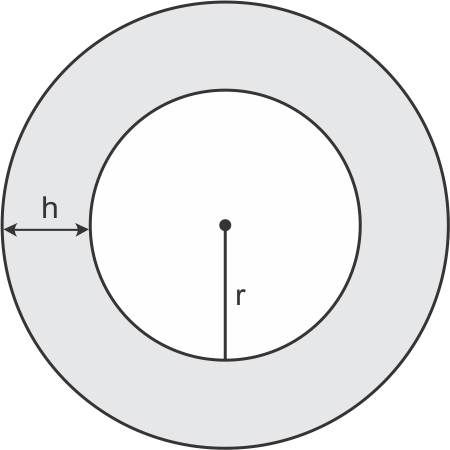
Solution 27

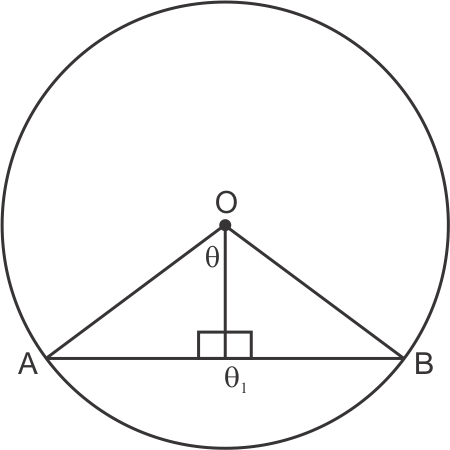
Solution 28
Correct option: (b)
area = circumference
πr2 = 2πr
r = 2 units
area = πr2
= 4π sq. units
Solution 29

Solution 30
** img pending

Solution 31

Solution 32

Areas Related to Circles Exercise 13.72
Solution 33
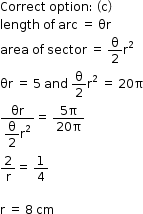
Solution 34

Solution 35
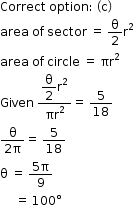
Solution 36
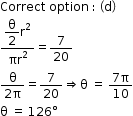
Solution 37

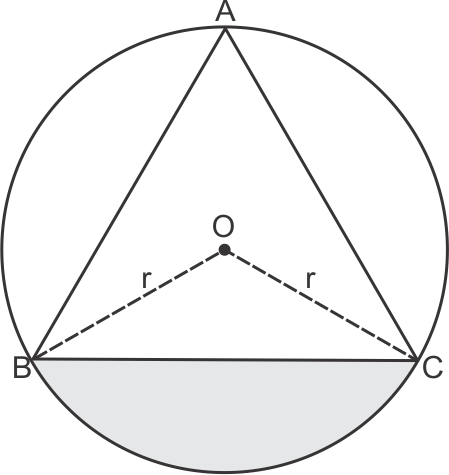
Areas Related to Circles Exercise 13.73
Solution 38
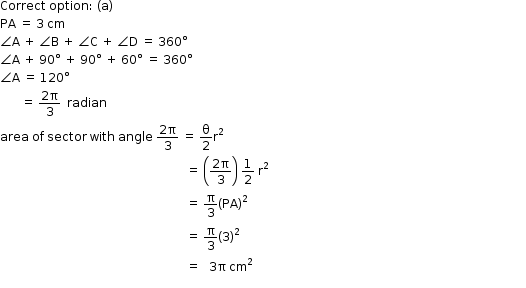
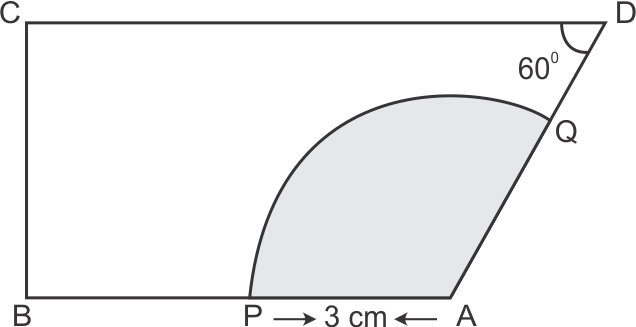
Solution 39

Solution 40

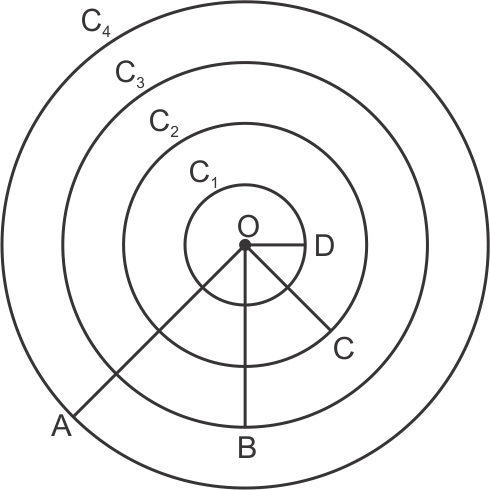
Solution 41

Solution 42

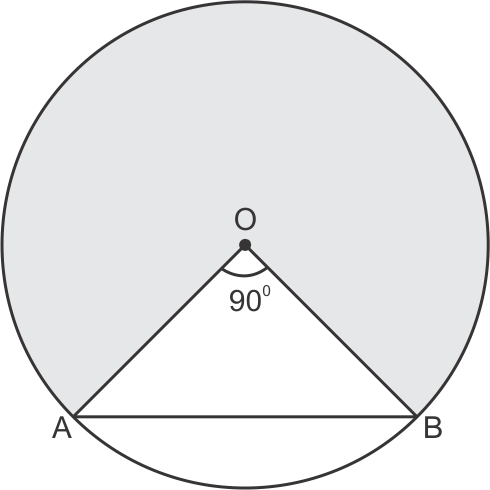
Solution 43

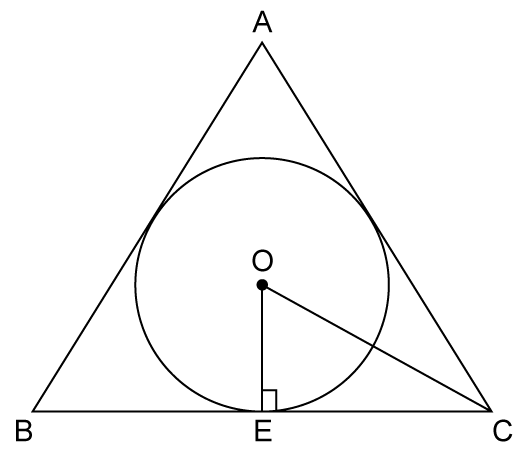
Areas Related to Circles Exercise 13.74
Solution 44

Solution 45

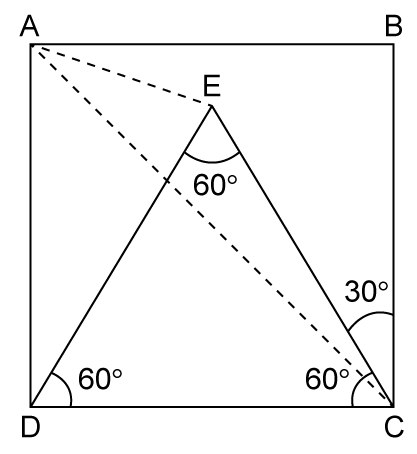
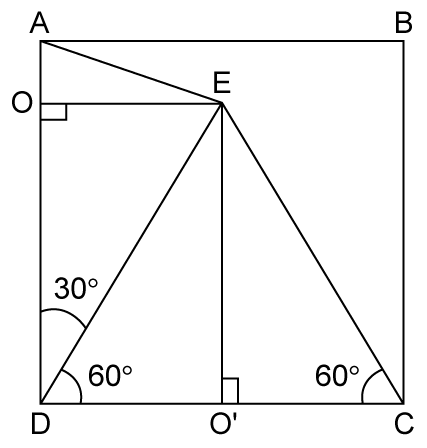
Solution 46
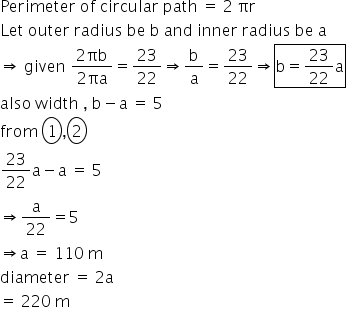
Correct option: (b)
radius of Circle = 5 cm
area = π (5)2
= 25 π
rdius of circle 2 = 12 cm
area = π (12)2
= 144 π
area of larger circle = 144 π + 25π
= 169 π
πr2 = 169 π
r2 = 169
r = 13
diameter = 2r
= 26
Solution 47

Solution 48

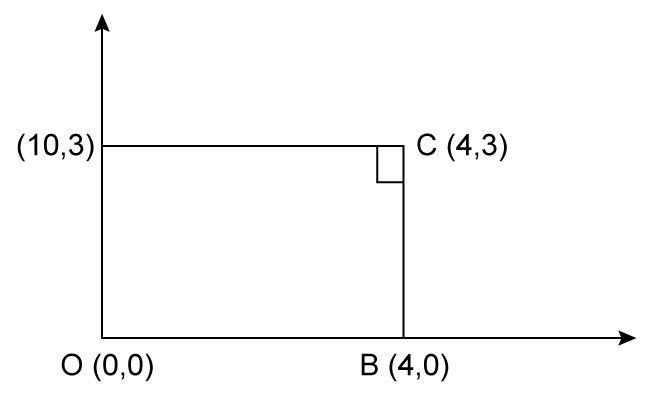
Solution 49
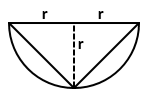
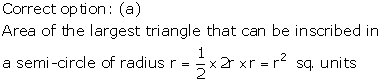
Solution 50

Solution 51

Solution 52

Solution 53