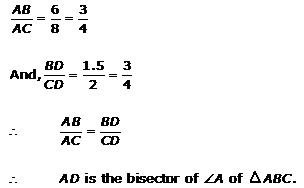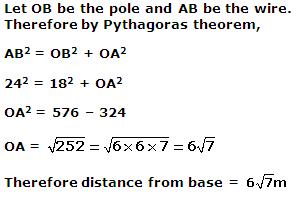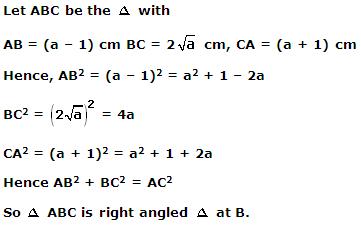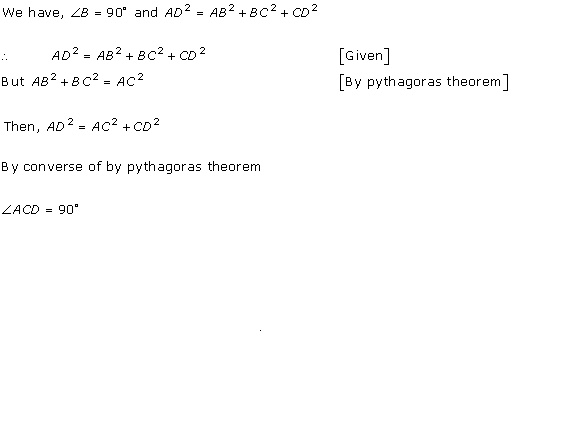Class 10 RD SHARMA Solutions Maths Chapter 7 - Triangles
Triangles Exercise Ex. 7.1
Solution 1
(i) All circles are similar.
(ii) All squares are similar.
(iii) All equilateral triangles are similar.
(iv) Two triangles are similar, if their corresponding angles are equal.
(v) Two triangles are similar, if their corresponding sides are proportional.
(vi) Two polygons of the same number of sides are similar, if (a) their corresponding angles are equal and (b) their corresponding sides are proportional.
Solution 2
(i) False
(ii) True
(iii) False
(iv) False
(v) True
(vi) True
Triangles Exercise Ex. 7.2
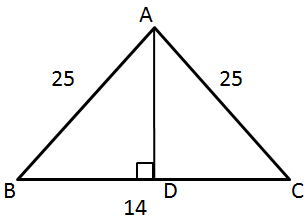
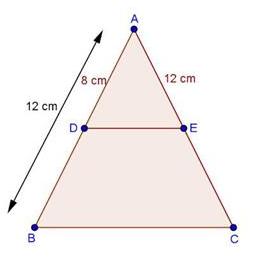
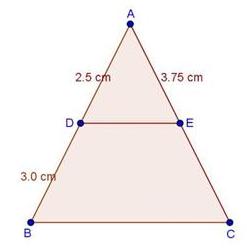
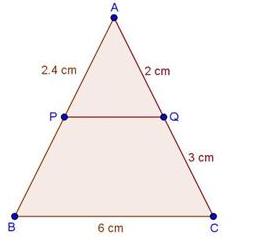
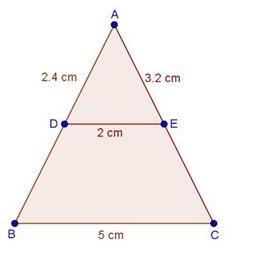
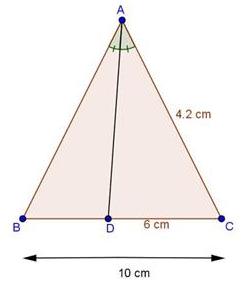
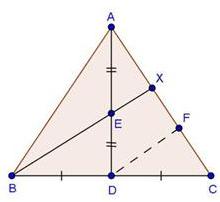
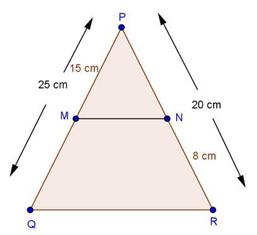
Solution 1(i)
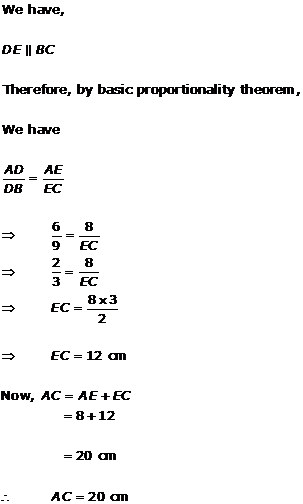
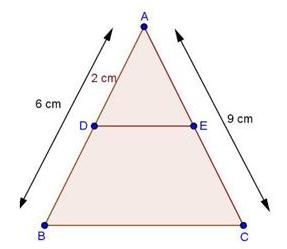
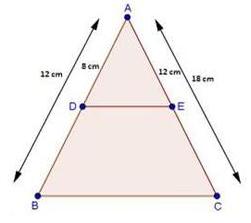
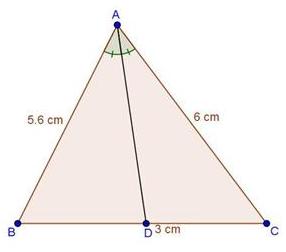
Solution 1(ii)
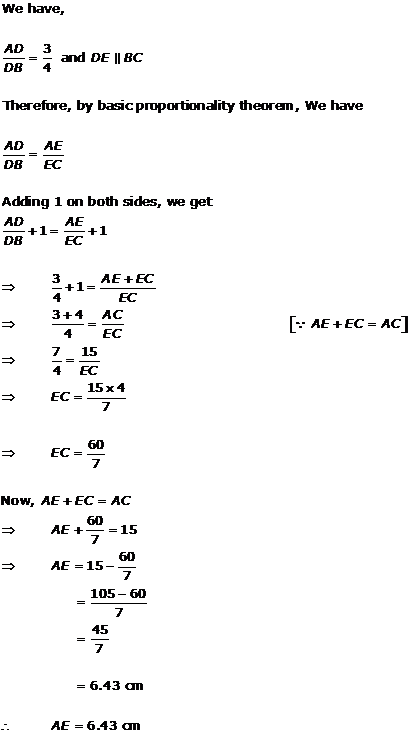
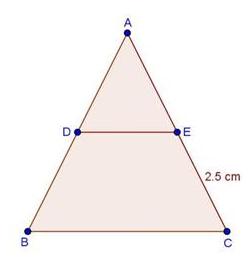
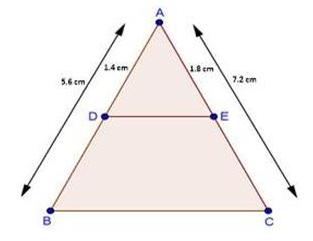
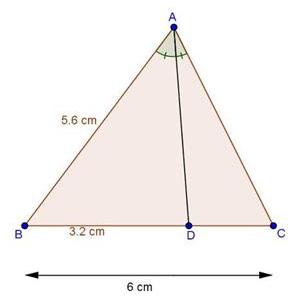
Solution 1(iii)
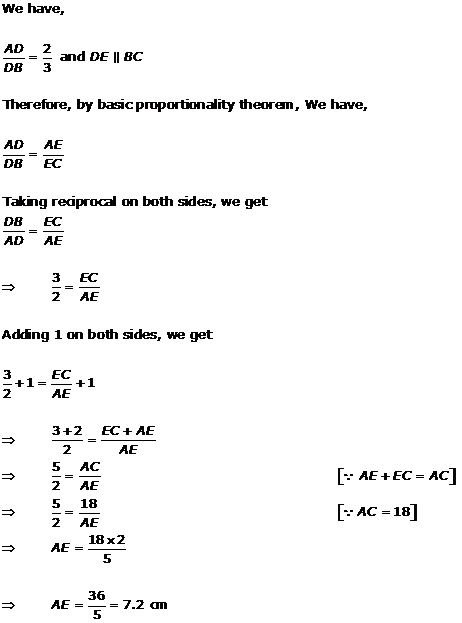
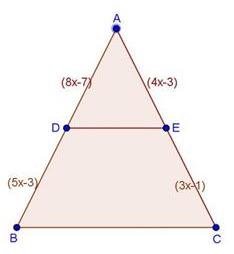
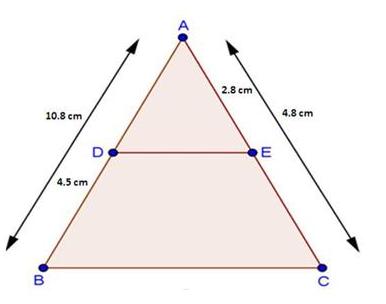
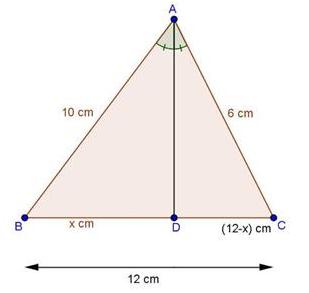
Solution 1(iv)
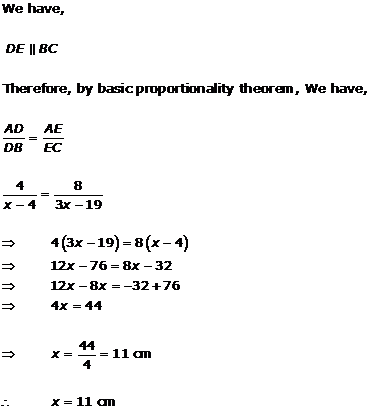
Solution 1(v)

Solution 1(vi)
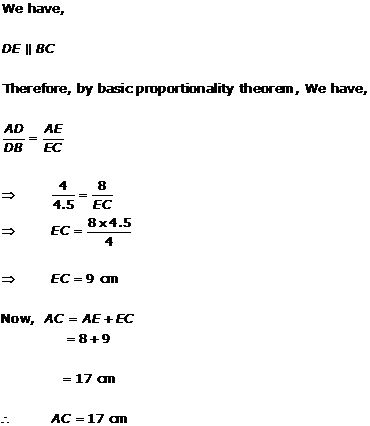
Solution 1(vii)
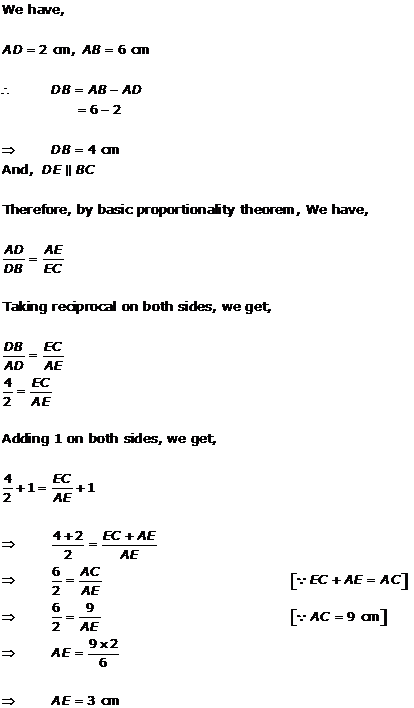
Solution 1(viii)
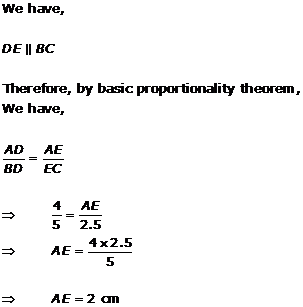
Solution 1(ix)

Solution 1(x)
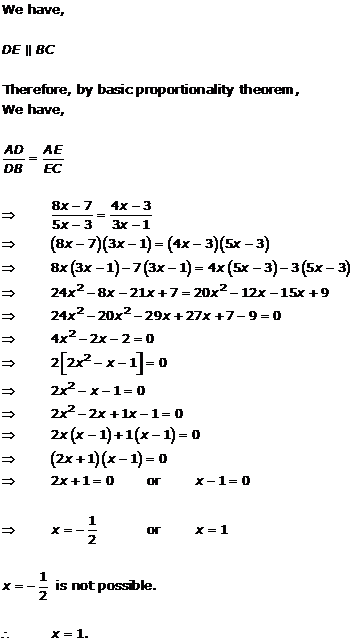
Solution 1(xi)
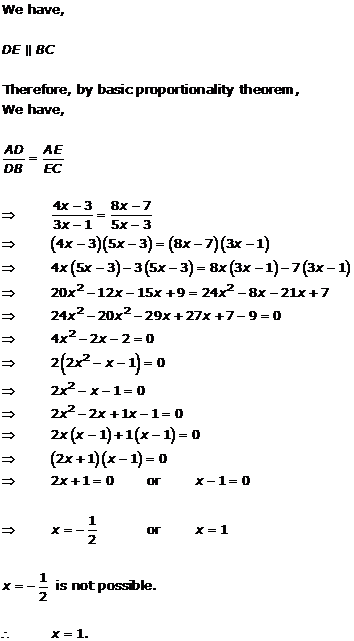
Solution 1(xii)
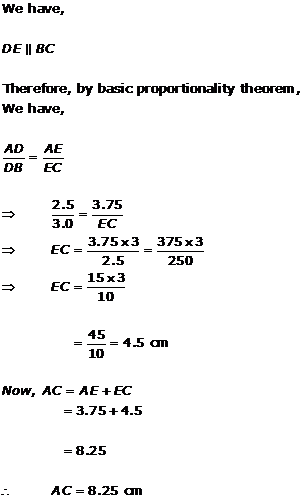
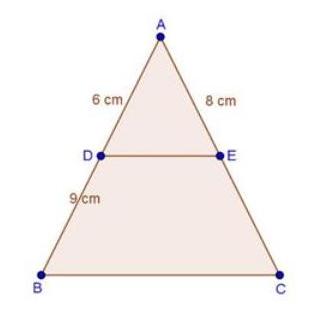
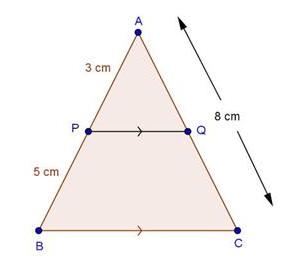
Solution 2(i)
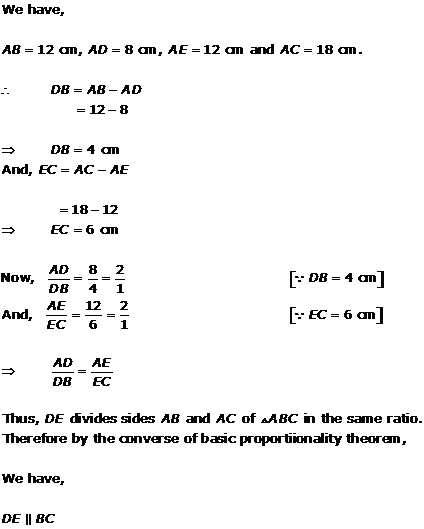
Solution 2(ii)
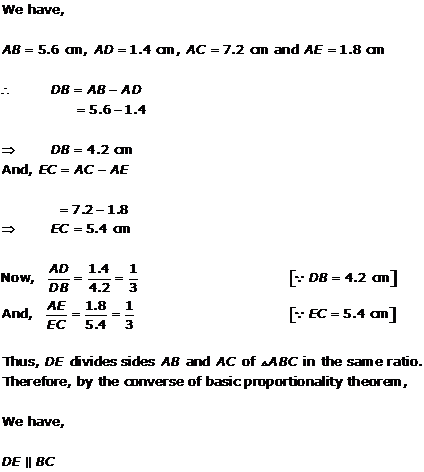
Solution 2(iii)
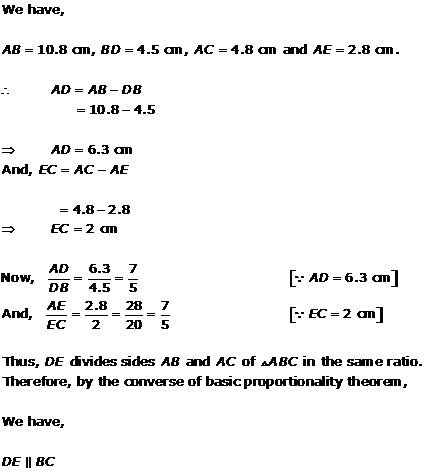
Solution 2(iv)
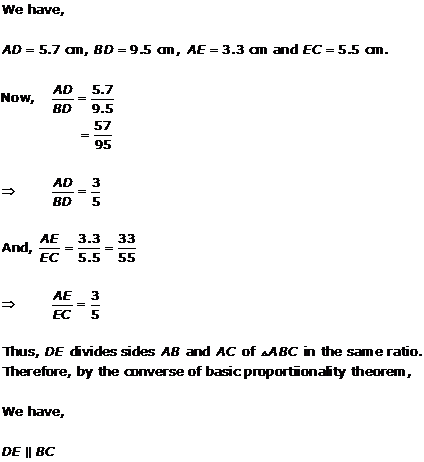
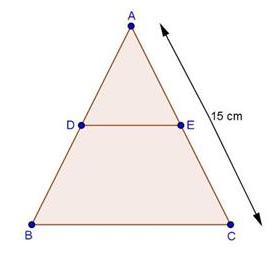
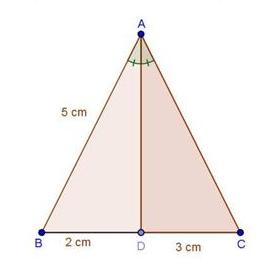
Solution 3
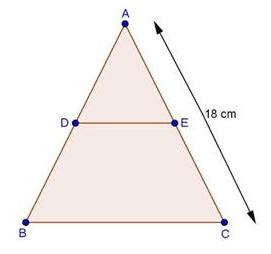
Solution 4

Solution 5
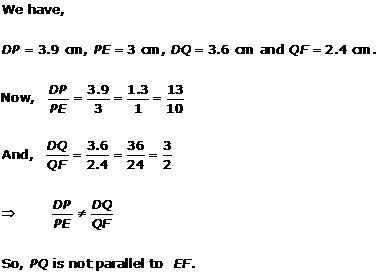
Solution 6
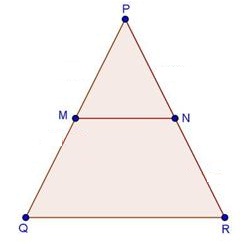

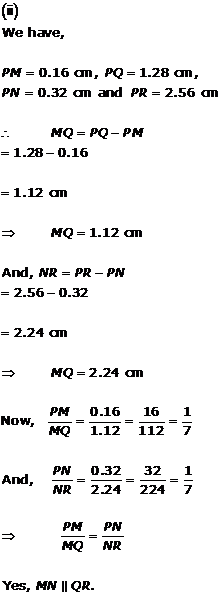
Solution 7
Solution 8
Triangles Exercise Ex. 7.3
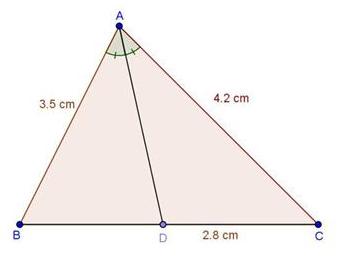
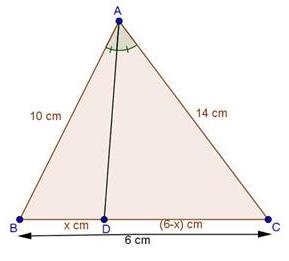
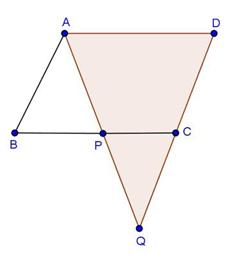
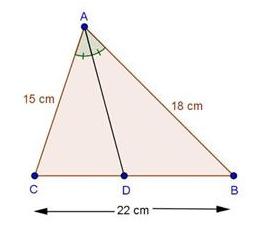
Solution 1(i)
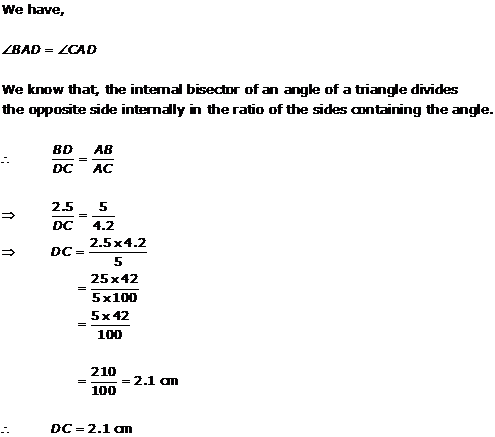
Solution 1(ii)

Solution 1(iii)
Solution 1(iv)
Solution 1(v)
Solution 1(vi)
Solution 1(vii)
Solution 1(viii)
Solution 2
Solution 3
Solution 4(i)
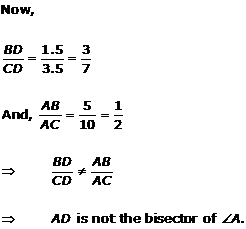
Solution 4(ii)
Solution 4(iii)
Solution 4(iv)
Solution 4(v)
Solution 5
Solution 6
Solution 7
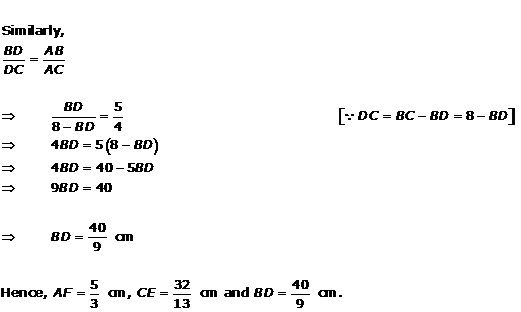
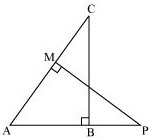
Triangles Exercise Ex. 7.4
Solution 1(i)

Solution 1(ii)

Solution 1(iii)
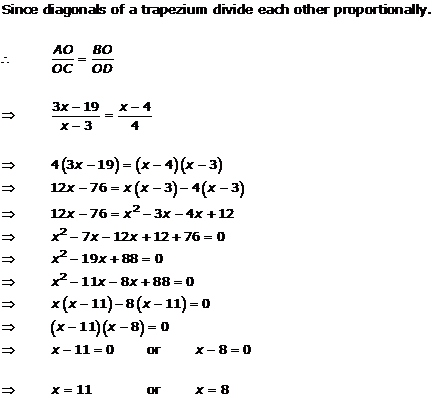
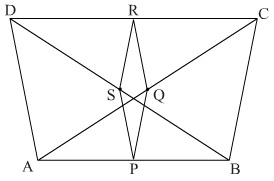
Triangles Exercise Ex. 7.5
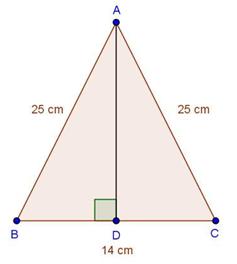
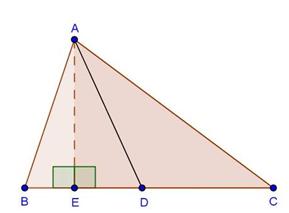
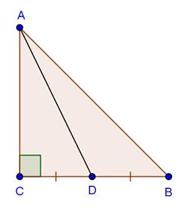
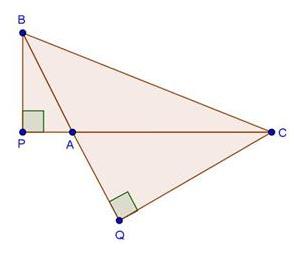
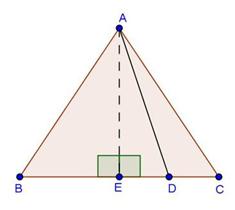
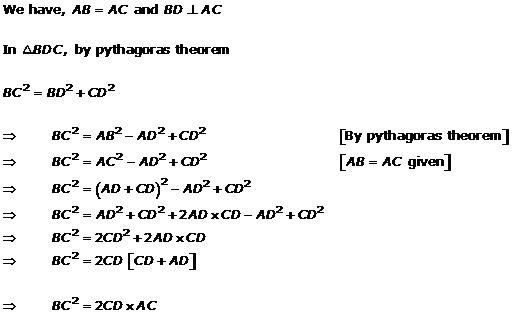
Solution 1
Solution 2
Solution 3
Solution 4
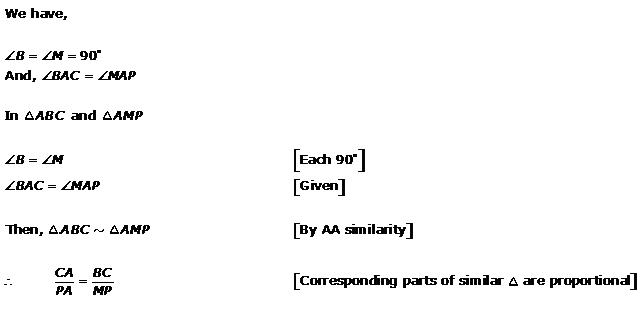
We have: ![]()
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
Solution 13
Solution 14
Solution 15
Solution 16
Solution 17
Solution 18
Solution 19
Solution 20
Solution 21
Solution 22
Solution 23
Solution 24
Solution 25
Triangles Exercise Ex. 7.6
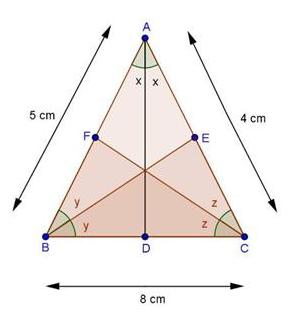
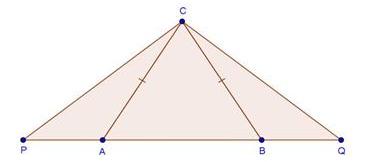
Solution 1(i)
Solution 1(ii)
Solution 1(iii)
Solution 1(iv)
Solution 1(v)
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
Solution 7
Solution 8(i)
Solution 8(ii)
Solution 8(iii)
Solution 9
Solution 10
Solution 11
Solution 12
Solution 13
Solution 14
Solution 15
Solution 16
Solution 17
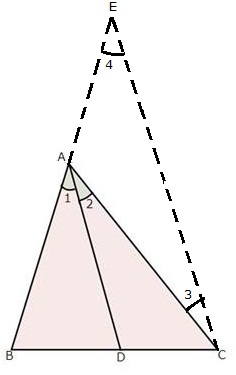
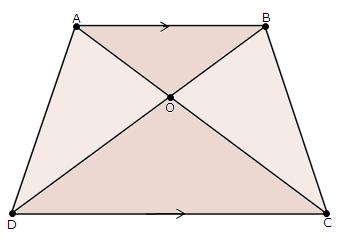
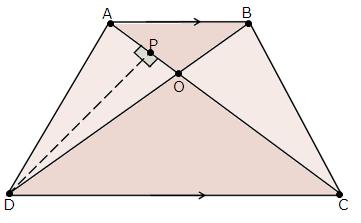
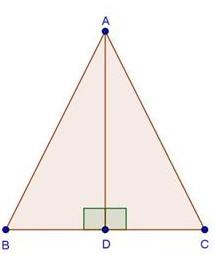
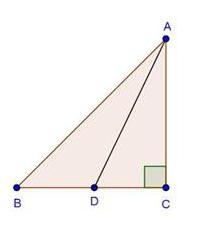
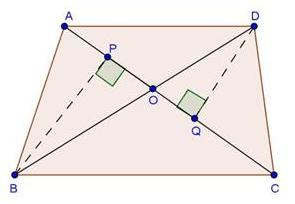
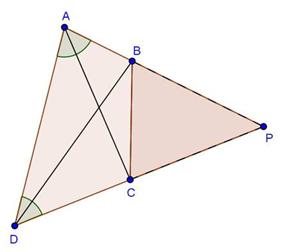
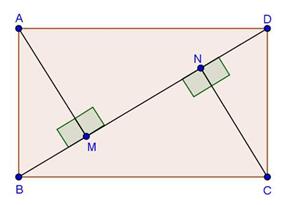
Solution 19
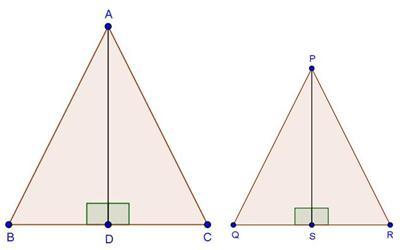
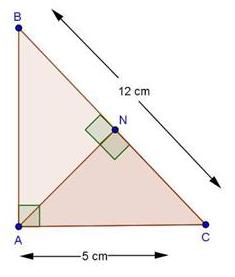
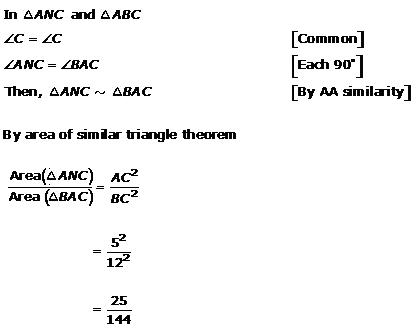
Since ![]() ABC and
ABC and ![]() DBC are one same base,
DBC are one same base,
Therefore ratio between their areas will be as ratio of their heights.
Let us draw two perpendiculars AP and DM on line BC.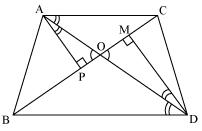
In ![]() APO and
APO and ![]() DMO,
DMO,![]() APO =
APO = ![]() DMO (Each is90o)
DMO (Each is90o)![]() AOP =
AOP = ![]() DOM (vertically opposite angles)
DOM (vertically opposite angles)![]() OAP =
OAP = ![]() ODM (remaining angle)
ODM (remaining angle)
Therefore ![]() APO ~
APO ~ ![]() DMO (By AAA rule)
DMO (By AAA rule)
Solution 20
Solution 21
Solution 22
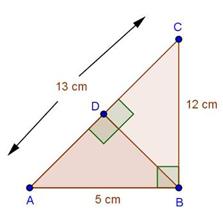
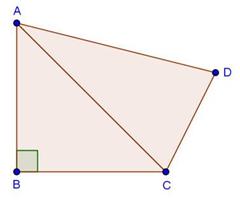
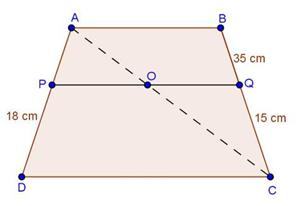
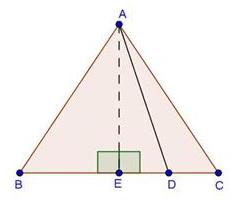
Solution 18
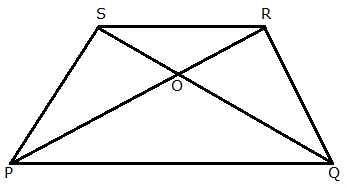
In trapezium PQRS, PQ || RS and PQ = 3RS.
![]() … (i)
… (i)
In ∆POQ and ∆ROS,
∠SOR = ∠QOP … [Vertically opposite angles]
∠SRP = ∠RPQ … [Alternate angles]
∴ ∆POQ ∼ ∆ROS … [By AA similarity criteria]
Using the property of area of areas of similar triangles, we have
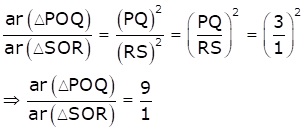
Hence, the ratio of the areas of triangles POQ and ROS is 9:1.
Triangles Exercise Ex. 7.7
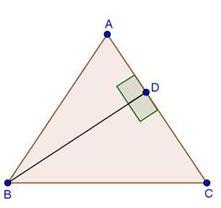
Solution 1

Solution 2(i)

Solution 2(ii)

Solution 2(iii)

Solution 2(iv)

Solution 3

Solution 4
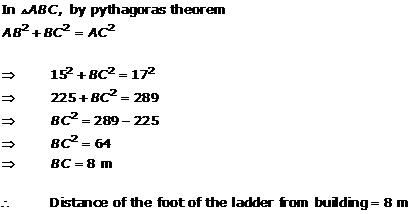
Solution 5

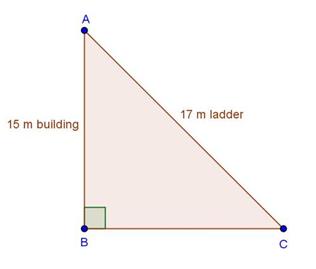
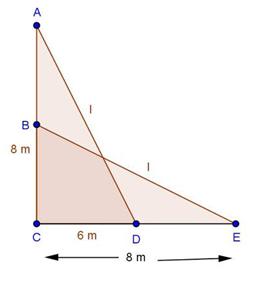
Let CD and AB be the poles of height 11 and 6 m.
Therefore CP = 11 - 6 = 5 m
From the figure we may observe that AP = 12m
In triangle APC, by applying Pythagoras theorem 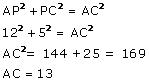
Therefore distance between their tops = 13 m.
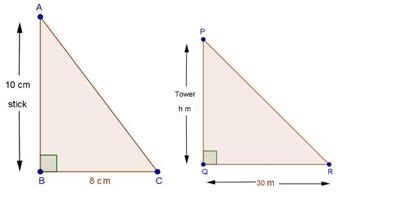
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
Solution 13
Solution 14
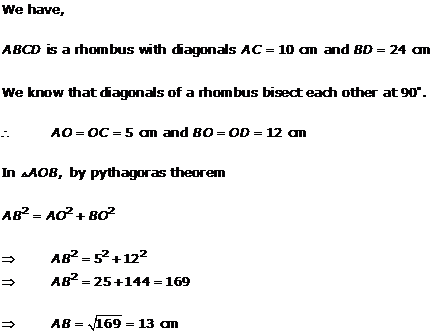
Solution 15
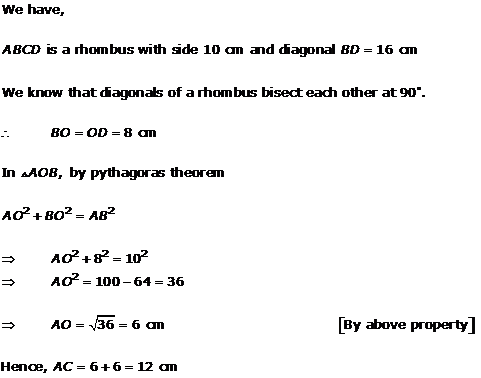
Solution 16
Solution 17
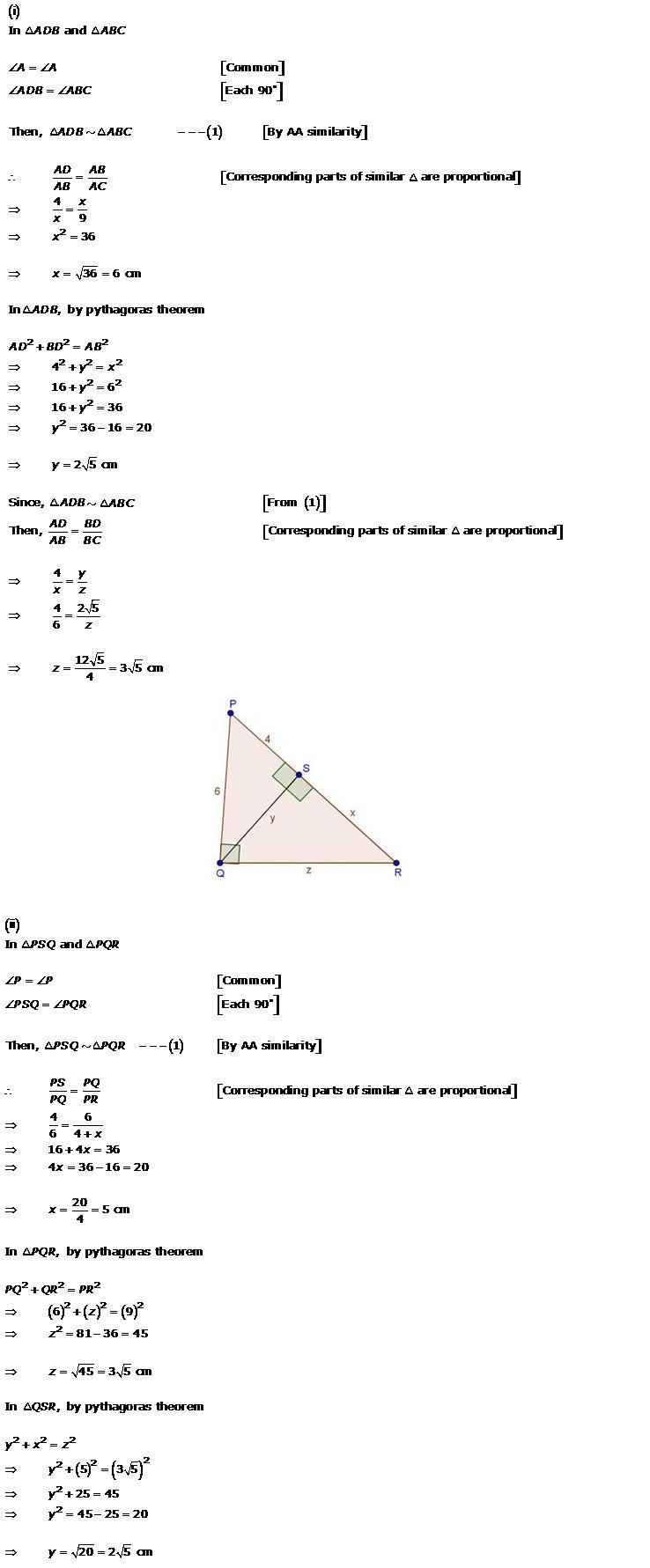
(i)
Solution 18
Solution 19

Solution 20
Solution 21
Solution 22
Solution 23
Solution 24
Solution 25
(i)
Solution 26
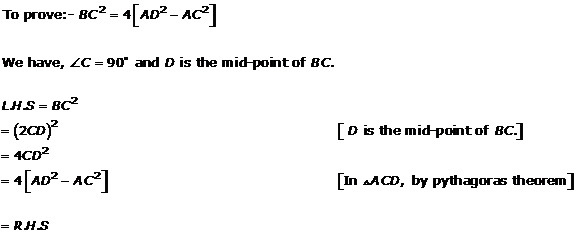
Solution 27
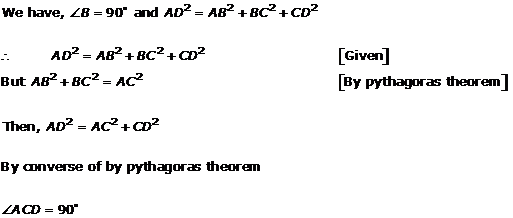
Solution 28
Triangles Exercise Rev. 7
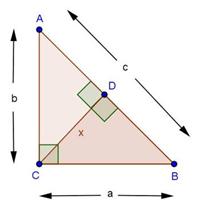
Solution 1(i)
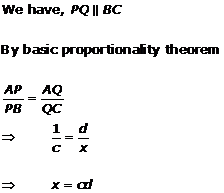
Solution 1(ii)
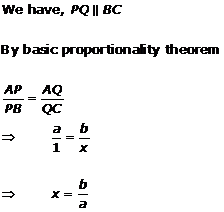
Solution 1(iii)
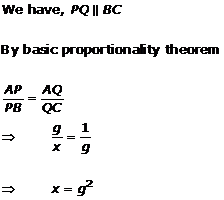
Solution 1(iv)
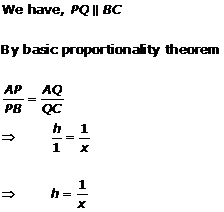
Solution 2
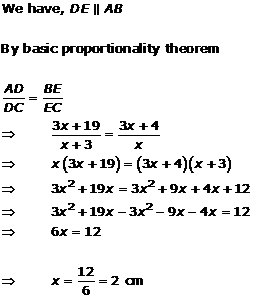
Solution 3
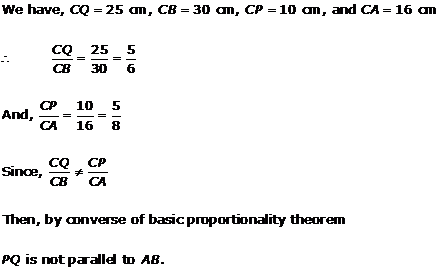
Solution 4
Solution 5
Solution 6
Solution 7(i)
Solution 7(ii)
Solution 7(iii)
Solution 7(iv)
Incomplete question (two triangles are not given in the figure).
Solution 7(v)
Incomplete question (two triangles are not given in the figure).
Solution 7(vi)
Solution 8

Solution 9
Solution 10
Solution 11
Solution 12
Solution 13
Solution 14
Solution 15

Solution 16
Solution 17
Solution 18
Solution 19
Solution 20
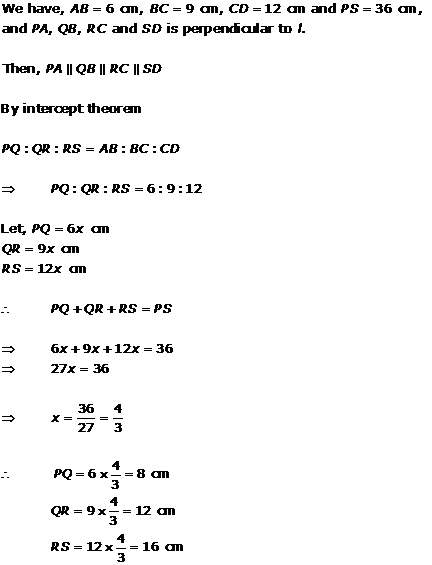
Solution 21
Solution 22
Solution 23
Solution 24
Solution 25
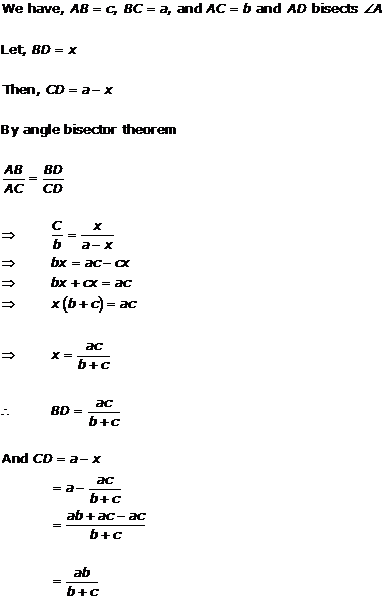
Solution 26
Solution 27
Solution 28
Solution 29
Solution 30
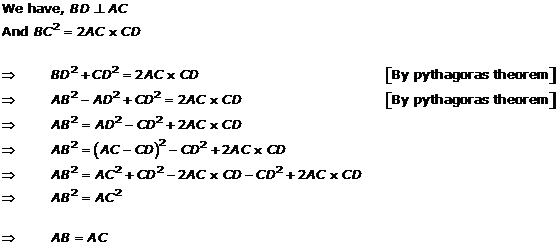
Solution 31
Solution 32
Solution 33
Solution 34
Solution 35
Solution 36
Solution 37
Solution 38
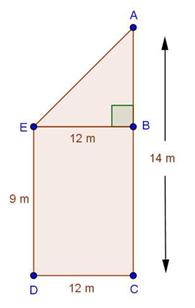
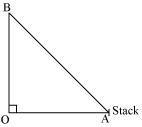
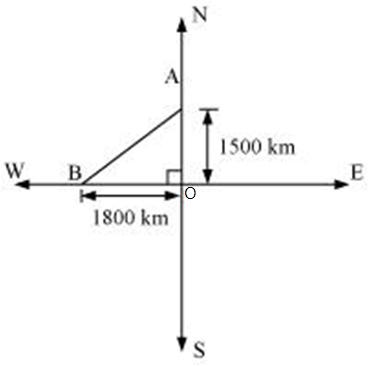
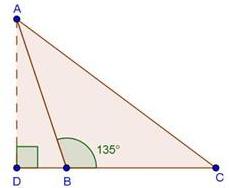
The given information can be represented by the figure given below.
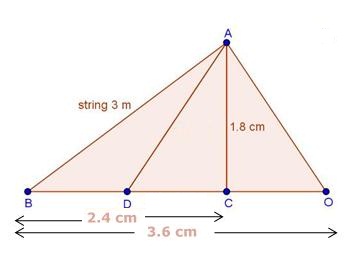
Triangles Exercise 7.131
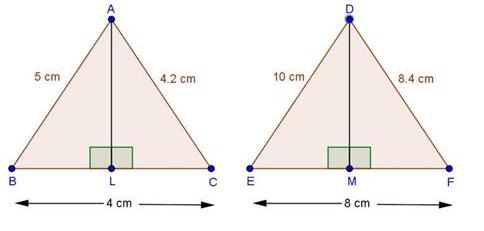
Solution 1
We know if sides of two similar triangles are in ratio a:b then area of these triangles are in ratio a2b2
According to question, ratio of sides= 4:9
Hence ratio of areas = 42:92
= 16:81
So, the correct option is (d).
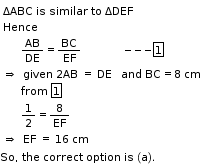
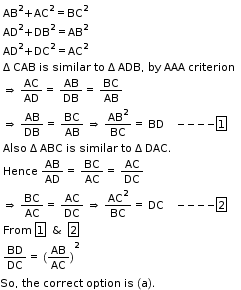
Solution 2

So, the correct option is (a).
Solution 3

Triangles Exercise 7.132
Solution 4
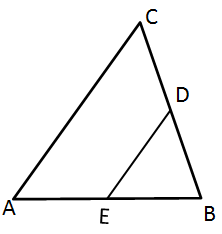

Solution 5
Solution 6
All these pairs of corresponding sides are in the same proportion so by SSS similarity criteria triangle ∆ABC are similar.
Given ratio of sides = 2.5
So, ratio of areas = 22:52
= 4:25
So, the correct option is (b).
Solution 7
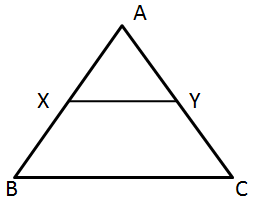

Solution 8
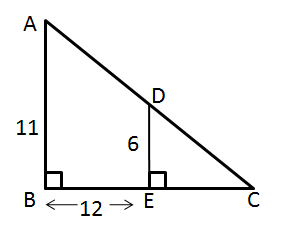

Solution 9
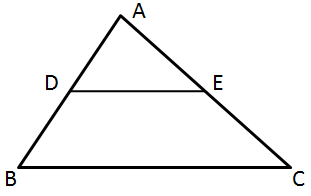
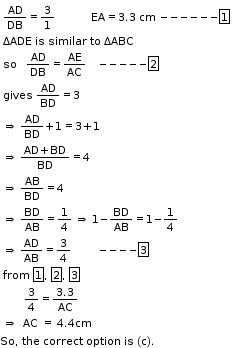
Solution 10

Solution 11

Solution 12

Solution 13
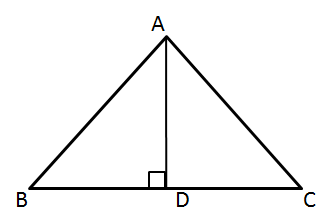

Solution 14
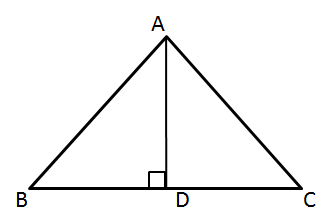

Solution 15
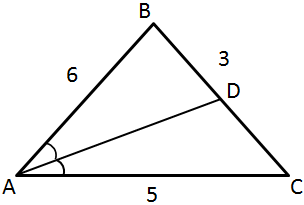

Solution 16
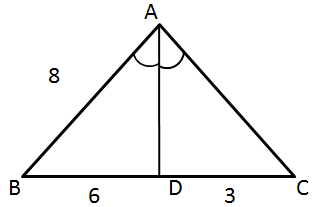

Solution 17
Triangles Exercise 7.133
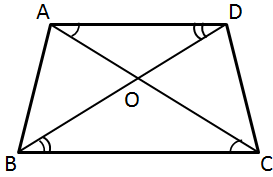
Solution 18

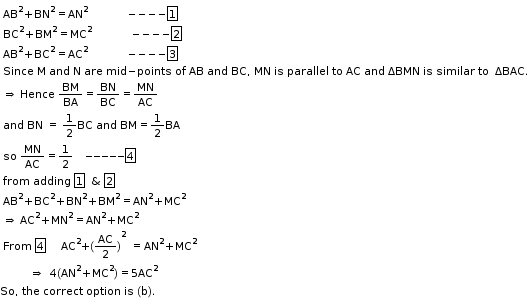
Solution 19
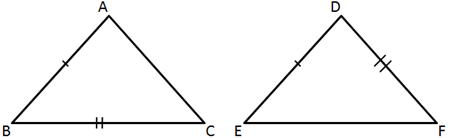
For triangles to be similar by SAS
∠B = ∠D
So, the correct option is (c).
Solution 20
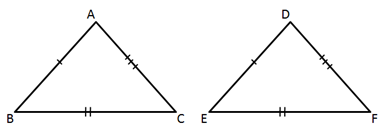

Solution 21
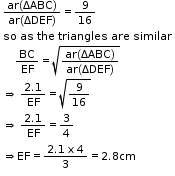
So, the correct option is (a).
Solution 22

Solution 23
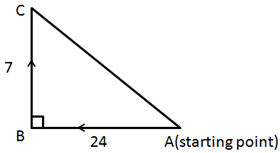

Solution 24
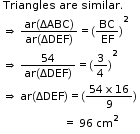
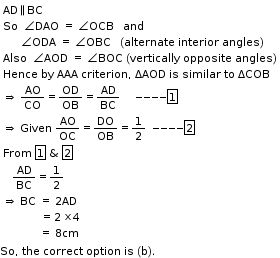
So, the correct option is (b).
Solution 25
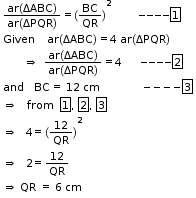
So, the correct option is (c).
Solution 26

Solution 27

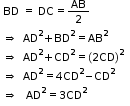
So, the correct option is (c).
Solution 28
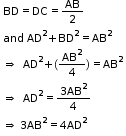
So, the correct option is (b).
Solution 29


Solution 30

Triangles Exercise 7.134
Solution 31

So, the correct option is (b).
Solution 32

Solution 33

Solution 34

Solution 35

Triangles Exercise 7.135
Solution 36
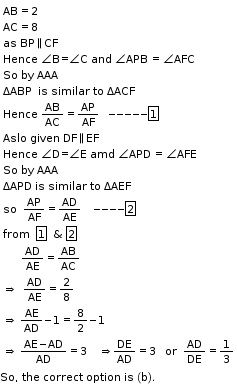
Solution 37

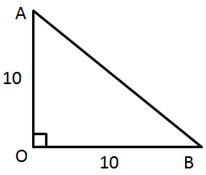
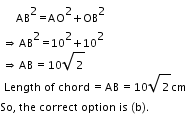
Solution 38

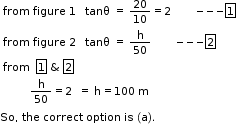
Solution 39

So, the correct option is (a).
Solution 40
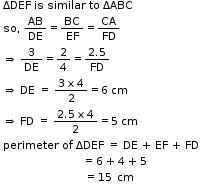
So, the correct option is (b).
Triangles Exercise 7.136
Solution 41
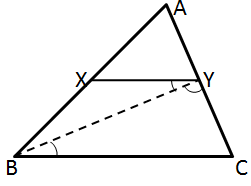

Solution 42
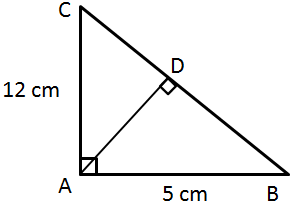

Solution 43
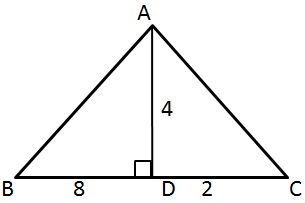

Solution 44


Solution 45


Solution 46
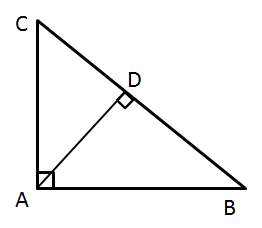
Solution 47


Solution 48


Solution 49

Solution 50

Solution 51