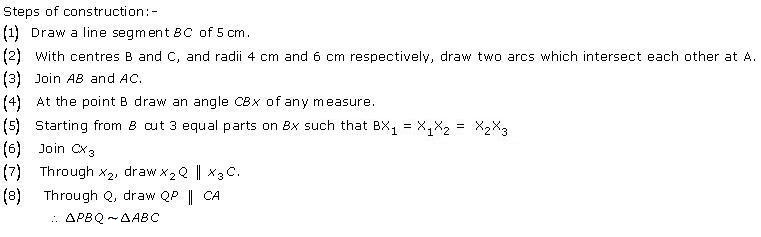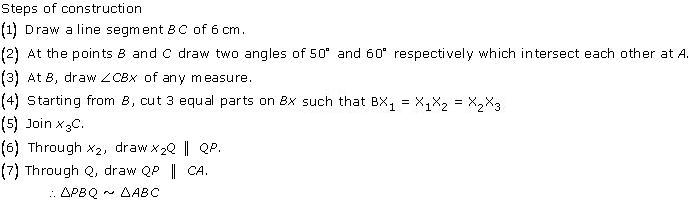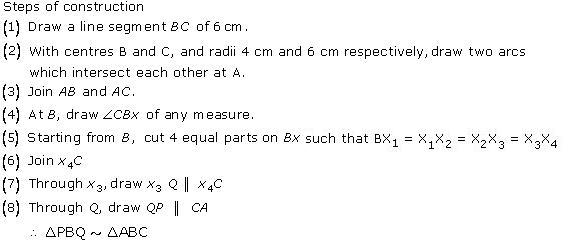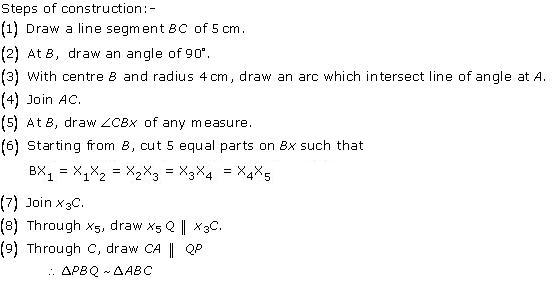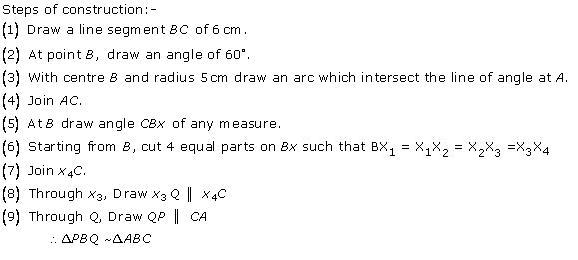Class 10 RD SHARMA Solutions Maths Chapter 9 - Constructions
Constructions Exercise Ex. 9.1
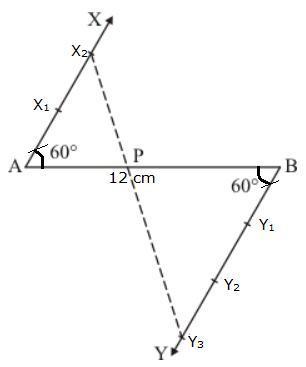
Solution 1

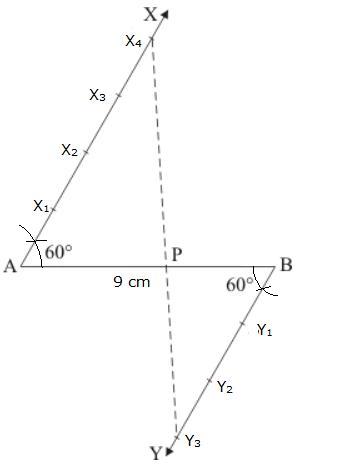
Solution 2

Solution 3
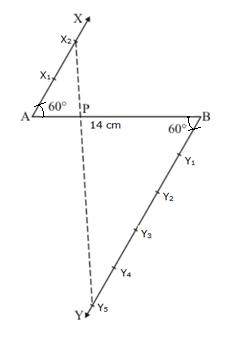
Solution 4

1. Draw segment AB of length 8 cm.
2. Draw any ray AX making acute angle ∠BAX with AB.
3. Draw BY parallel to AX by making ∠ABY = ∠BAX.
4. Mark four points A1, A2,…..,A4 on AX and five points B1, B2,…..,B5 on BY such that AA1=A1A2=…..= A3A4=BB1=B1B2=….=B4B5
5. Join A4B5; it intersects AB at P. P divides AB in the ratio 4:5.
Constructions Exercise Ex. 9.2
Solution 1
Solution 2
Solution 3
Solution 4
Solution 5

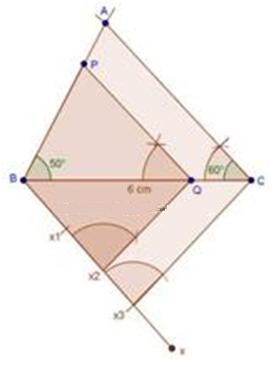
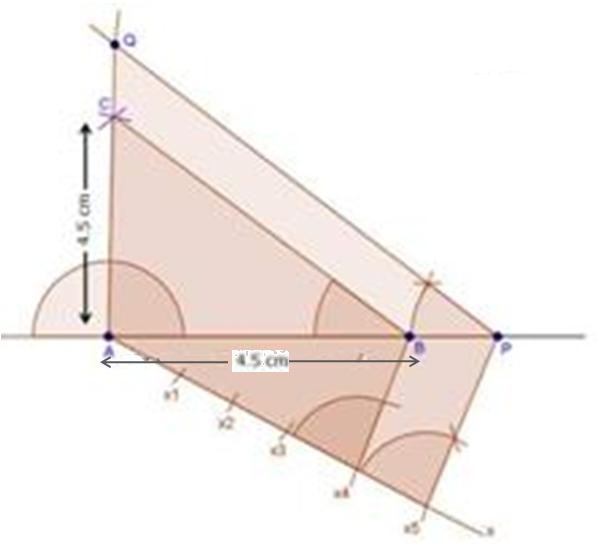
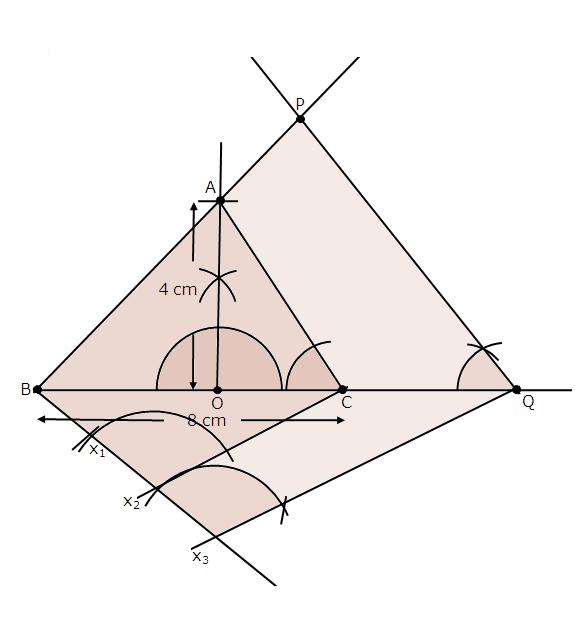
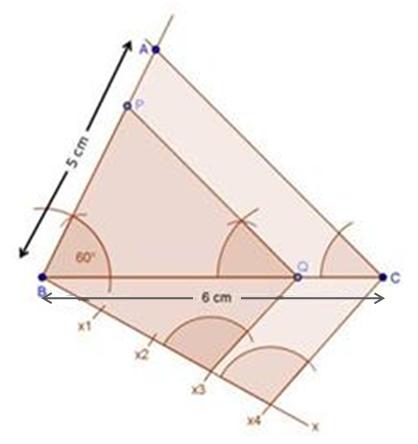
Steps of construction
(1) Draw a line segment BC with 6 cm.
(2) Taking centres B and C and radii 5 cm and 7 cm respectively, draw two arcs (one from each centre) which intersect each other at A.
(3) Join AB and AC.
(4) At B, draw an angle CBX of any acute measure.
(5) Starting from B, cut 3 equal parts on BX such that BX1 = X1X2 = X2X3 = X3X4 = X4X5 = X5X6 = X6X7.
(6) Join X7C.
(7) Through X5, draw X5Q ‖ X7C.
(8) Through Q, draw QP ‖ CA.
∴ ∆PBQ ∼ ∆ABC.
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
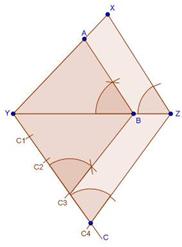
Solution 12
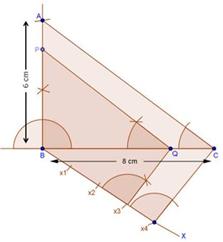

Solution 13
Steps of construction:
- Draw a line segment AB = 6.5 cm
- With A as the centre and radius AC = 5.5 cm, draw an arc.
- With B as the centre and radius BC = 5 cm, draw an arc intersecting the arc drawn in step 2 at C
- Join AC and BC to obtain ∆ABC.
- Below AB make an acute ∠BAX.
- Along AX, mark off five points as the sides of triangle to be 3/5th of original triangle, the sides to be divided into five equal parts. Mark A1, A2, A3, A4, A5 along AX such that AA1 = A1A2 = A2A3 = A3A4 = A4A5
- Join A5B.
- Consider three parts out of five equal parts on AX. From point A3, draw A3B' ∥ A5B meeting AB at B' such that ∠AA5B = ∠AA3B'.
- From B', draw B'C' ∥ BC meeting AC at C' such that ∠ABC = ∠AB'C'
- ∆AB'C' is the required triangle, each of whose sides is 3/5th of the corresponding sides of ∆ABC

Solution 14
Steps of construction:
- Draw a line segment PQ = 6 cm
- To construct ∠ PQR = 60°, taking Q as the centre and with an arbitrary radius draw an arc cutting PQ on S.
- Taking S as the centre, and the same radius, draw an arc cutting the previous arc at T. Join Q and T, extend QT further.
- With Q as the centre and a radius of 7 cm, draw an arc on the extended line segment QT at R.
- Join PR and QR to obtain ∆PQR.
- Below PQ make an acute angle QPX.
- Along PX, mark off five points as the sides of triangle to be 3/5th of original triangle, the sides to be divided into five equal parts. Mark P1, P2, P3, P4, P5 along PX, such that PP1 = P1P2 = P2P3 =P3P4 = P4P5.
- Join P5Q.
- Consider three parts out of the five equal parts on PX. From point P3, draw P3Q' ∥ P5Q meeting PQ at Q' by making ∠QP5P = ∠Q'P3P
- From Q', draw Q'R' ∥ QR by making ∠PQR = ∠ PQ'R'
- ∆PQ'R' is the required triangle, each of whose sides is 3/5th of the corresponding sides of ∆PQR

Solution 15
1. Draw ∆ABC with base BC = 6cm, AB = 5 cm and∠ABC = 60˚.
2. Draw any ray BX making acute angle ∠ABX with BC.
3. Mark four points B1, B2,B3,B4 on BY such that BB1=B1B2=B2B3=B3B4.
4. Join CB4 and draw a line parallel to CB4, through B3, to intersect AC at C'.
5. Join AC, and draw a line parallel to AC, through C', to intersect AB at A'.
6. ∆A'BC' is the required triangle.
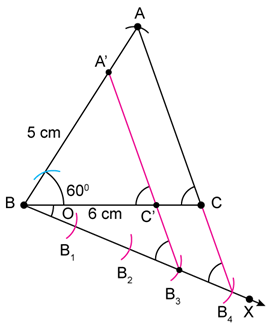
Solution 16
1. Draw AB = 4cm.
2. Draw RA perpendicular to AB, and mark C on it such that AC = 3 cm.
3. Join BC. DABC is the required triangle.
4. Draw any ray AX making acute angle ∠BAX with AB.
5. Mark five points A1, A2,…..,A5 on AX.
6. Join BA5, and draw a line parallel to it passing from A3, intersecting AB at B'.
7. Draw line parallel to CB through B' to intersect AC at C'.
8. ∆AB'C' is the required triangle.

Solution 17

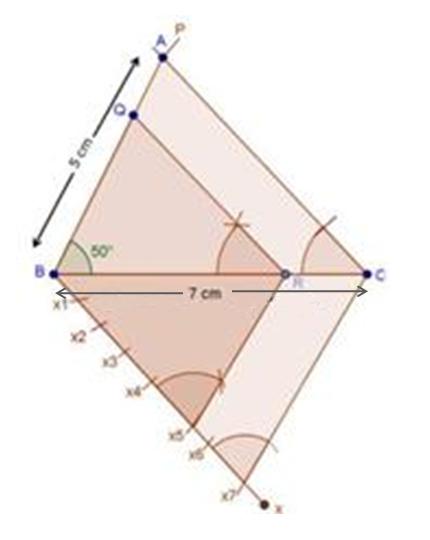
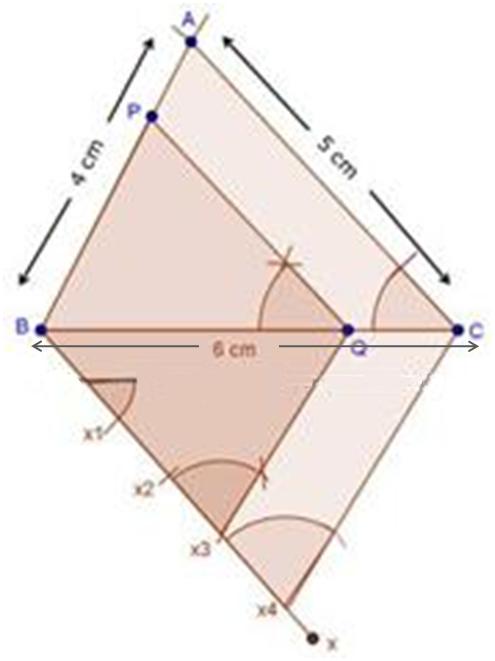
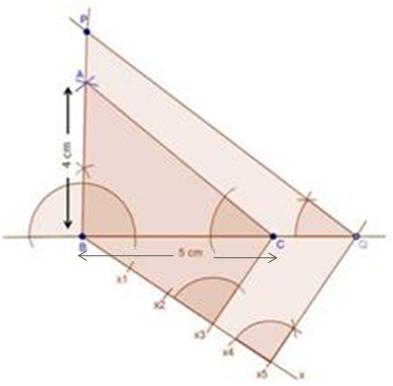
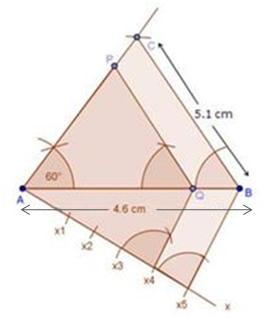
Steps of construction
(1) Draw a line segment BC with 5 cm.
(2) Taking centres B and C with equal radii 5 cm, draw two arcs (one from each centre) which intersect each other at A.
(3) Join AB and AC.
(4) At B, draw an angle CBX of any acute measure.
(5) Starting from B, cut 3 equal parts on BX such that BX1 = X1X2 = X2X3.
(6) Join X3C.
(7) Through X2, draw X2Q ‖ X3C.
(8) Through Q, draw QP ‖ CA.
∴ ∆PBQ ∼ ∆ABC.
Constructions Exercise Ex. 9.3
Solution 1

Solution 2
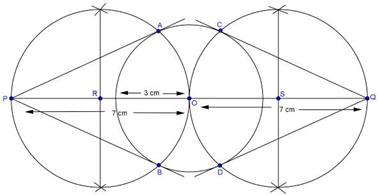

Solution 3
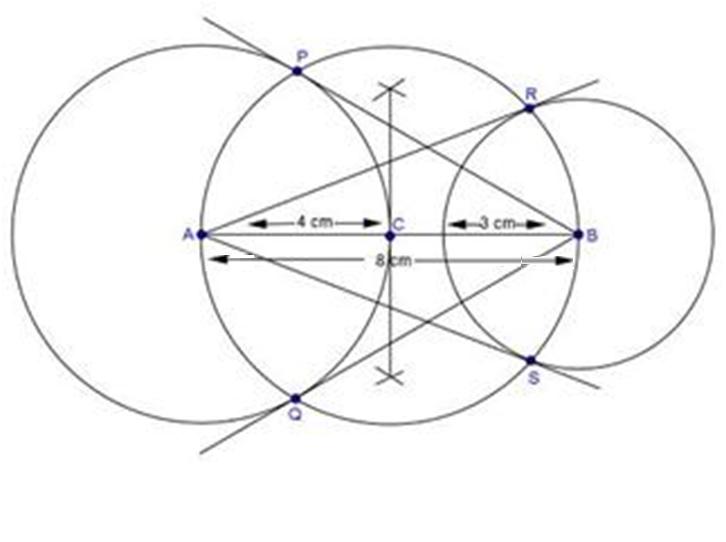

Solution 4
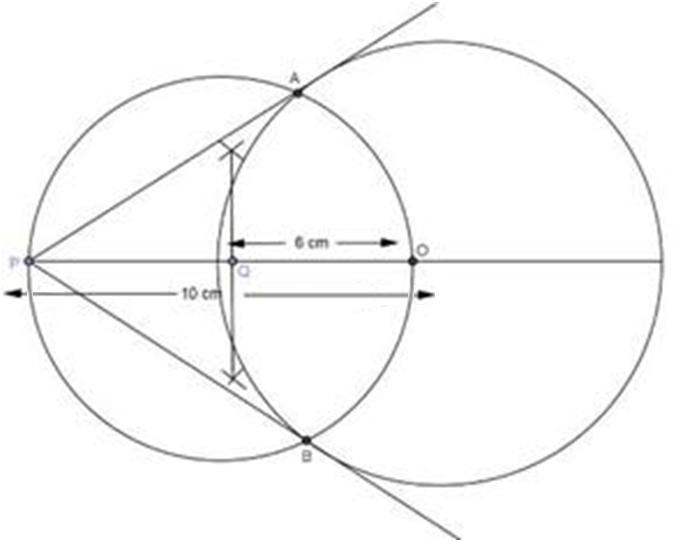
Steps of construction:
- Construct a line segment OP of length = 6.2 cm
- Taking O as the centre, construct a circle of radius3.5 cm.
- Taking O and P as the centres, draw arcs of circles above and below OP intersecting each other at points R and S respectively.
- Draw the perpendicular bisector of OP by joining A and B. Mark the midpoint of OP as Q.
- Taking Q as the centre draw a circle of radius OQ or PQ and mark the points of intersection of the two circles as A and B.
- Join PA and extend it on both the sides.
Join PB and extend it on both the sides
PA and PB are the required tangents.
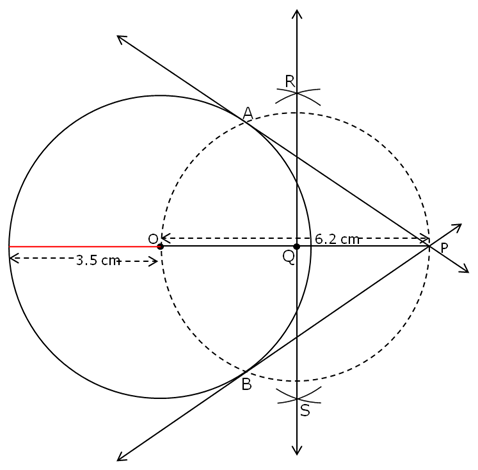
Solution 5
- Draw a circle having a centre O and a radius of 4.5 cm.
- Take point P on the circle and join OP.
-
Angle between the tangents = 45°
Hence, the angle at the centre
= 180° - 45° = 135° (supplement of the angle between the tangents)
∴Construct m∠POQ = 135°
- Keeping a radius of 4.5 cm, draw arcs of circle taking the points P, and Q as the centres.
- Name the points of intersection of arcs and circle as A and C respectively.
- Taking A as the centre, and with the same radius mark B such that OA = AB.
- Similarly, taking C as the centre and with the same radius mark D such that OC = CD.
- Taking A and B as the centres and the same radius draw two arcs intersecting each other at U.
- Join P, S and U and extend it on both the sides to draw a tangent at point P.
- Taking C and D as the centres and the same radius draw two arcs intersecting each other at V.
- Join Q, T and V and extend it on both the sides to draw a tangent at point Q.
- Extended tangents at P and Q intersect at R.
-
Hence, the required tangents are UR and VR such that the angle between them is 45°.

Solution 6
Steps of construction:
- Draw a line segment BC = 8 cm.
- Measure m∠B = 90˚ at point B.
- Taking B as the centre and a radius of 6 cm, draw an arc and hence, construct AB = 6 cm
- Join AC. Hence, ∆ABC right angled at B is constructed.
- Taking B as the centre and a radius more than BD, draw two arcs cutting AC at points E and F.
- Taking E and F as centres draw arcs to intersect each-other at P and Q respectively. Join and extend PQ on both the sides. This is the perpendicular BD from B on AC.
- BD⊥CD, hence, ∆BCD is a right angled triangle. Therefore the circle passing through points B, C and D has the hypotenuse BC as the diameter.
- Construct a circle by taking O, the midpoint of BC as the centre (BC is the diameter of the circle)
- OB ⊥ AB, extend AB on both the sides. OB is one of the tangents passing through point A and tangent at point B.
- Join OA. Take the centre of OA by drawing intersecting arcs from point O and A and which intersect at points R and S respectively.
- Join RS. The point at which RS intersects OA is G.
- Taking G as the centre and radius OG, construct a circle.
- The point of intersection of the two circles is H.
- Join H and A. Now extend AH on both the sides. AH is the second tangent drawn from point A.

Solution 7


Constructions Exercise Ex. MCQs
Solution 1
The figure formed by two tangents and the two radii at points of contact, is a quadrilateral.
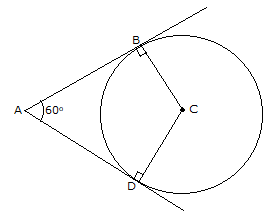
ABCD is a quadrilateral where ∠ABC = 90o and ∠ADC = 90o
Therefore, ∠BAD + ∠BCD = 180o
∴ ∠BCD = 120o
Hence, the angle between them should be 120o.
Solution 2
The minimum number of points required to divide a line segment in the ration 5 : 7, is (5 + 7 =) 12.
Hence, option (d) is correct.
Solution 3
The minimum number of points required to divide a line segment in the ratio m : n is m + n.
Hence, option (b) is correct.
Solution 4
The figure formed by two tangents and the two radii at points of contact, is a quadrilateral.
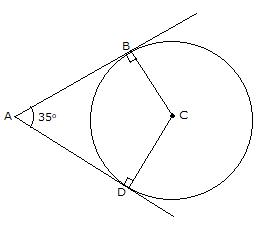
ABCD is a quadrilateral where ∠ABC = 90o and ∠ADC = 90o
Therefore, ∠BAD + ∠BCD = 180o
∴ ∠BCD = 145o
Hence, the angle between them should be 145o.
Solution 5
The minimum number of points to be located at equal distances on ray BX is (Max{8, 5} =) 8.
Hence, option (b) is correct.
Solution 6
As the line segment AB is divided in the ratio 4 : 7.
The minimum number of points required to is (4 + 7 =) 11.
So, B should be joined to A11.
Hence, option (b) is correct.
Solution 7
The similar triangle has sides 3/7 of the original ∆ABC.
After locating points B1, B2, B3, … B7 on BX at equal distances.
The next step is join B7 to C.
Hence, option (c) is correct.
Solution 8
The line segment AB is divided in the ratio 5 : 6.
Locate points A1, A2, … A5 on AX and B1, B2, … B6 on BY as A:B = 5:6.
So, the points joined to be are A5 and B6.
Hence, option (a) is correct.