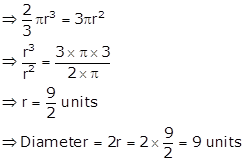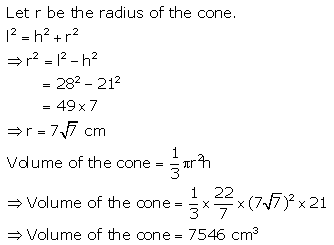Class 9 R S AGGARWAL AND V AGGARWAL Solutions Maths Chapter 15 - Volume and Surface Area of Solids
Choosing the correct option for multiple choice questions in your Maths exam requires practice. For chapter revision, you can refer to TopperLearning’s RS Aggarwal and V Aggarwal Solutions for CBSE Class 9 Maths Chapter 15 Volume and Surface Area of Solids. The solutions by some of the best Maths experts will help you relearn concepts such as the total surface area of a cube, volume of a cube, volume of a cylinder etc.
With our chapter solutions, get clarity on application-type questions such as calculating the concrete mixture for building a pillar. Besides, our CBSE Class 9 Mathematics videos and sample papers will be useful during Maths exam preparation.
Volume and Surface Area of Solids Exercise MCQ
Solution 1
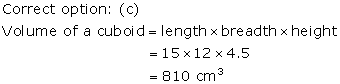
Solution 2
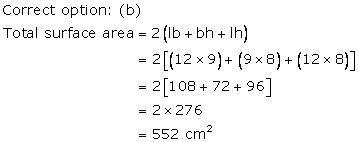
Solution 3

Solution 4
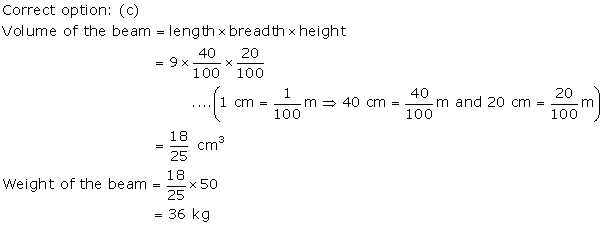
Solution 5

Solution 6

Solution 7
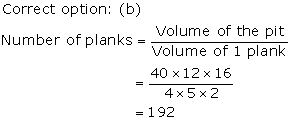
Solution 8

Solution 9

Solution 10
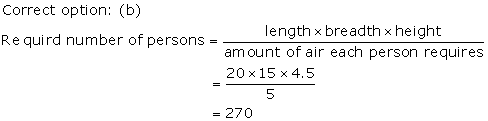
Solution 11

Solution 12
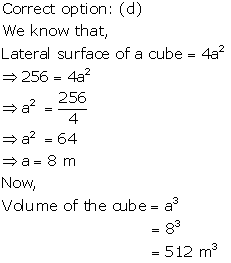
Solution 13

Solution 14

Solution 15
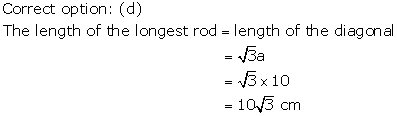
Solution 16

Solution 17

Solution 18
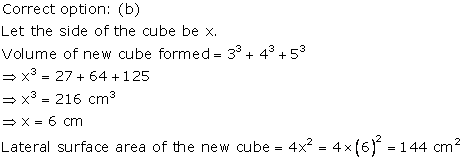
Solution 19

Solution 20

Solution 21

Solution 22

Solution 23
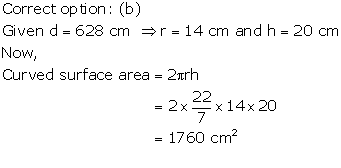
Solution 24

Solution 25

Solution 26

Solution 27

Solution 28
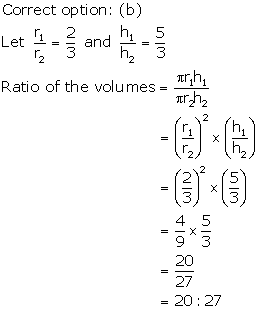
Solution 29

Solution 30

Solution 31

Solution 32
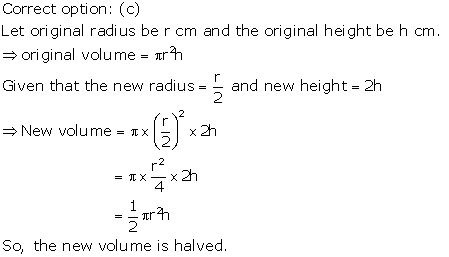
Solution 33
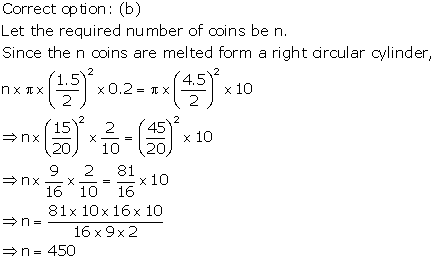
Solution 34

Solution 35

Solution 36

Solution 37
![]()
Solution 38
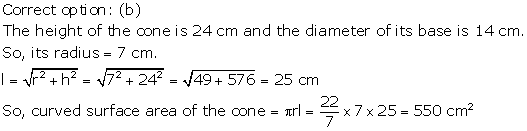
Solution 39
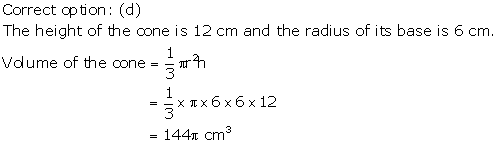
Solution 40

Solution 41

Solution 42
Correct option: (b)
Solution 43
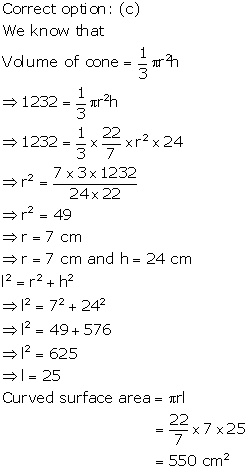
Solution 44

Solution 45

Solution 46

Solution 47

Solution 48

Solution 49

Solution 50

Solution 51

Solution 52

Solution 53

Solution 54

Solution 55
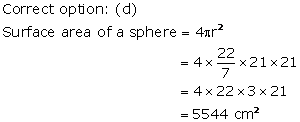
Solution 56
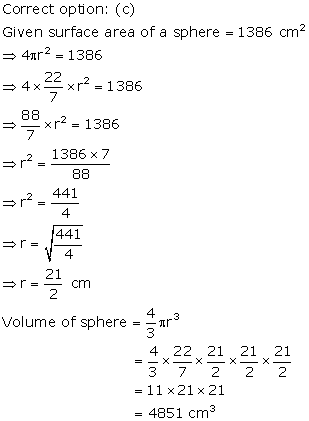
Solution 57

Solution 58

Solution 59
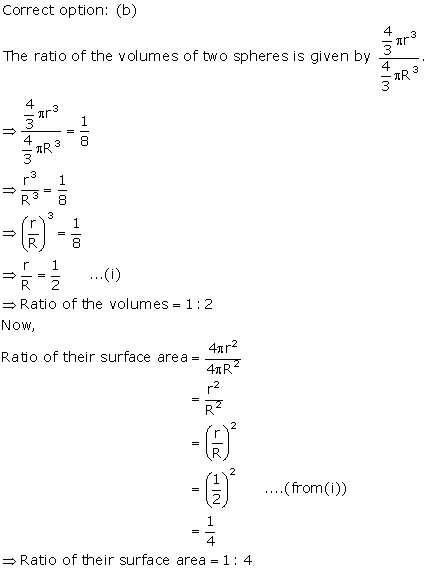
Solution 60

Solution 61
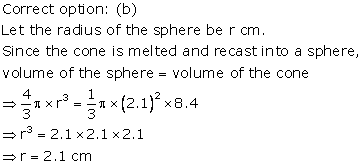
Solution 62

Solution 63
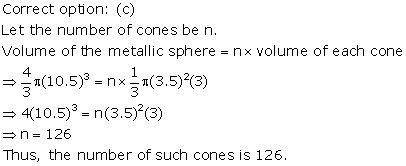
Solution 64

Solution 65

Solution 66

Solution 67
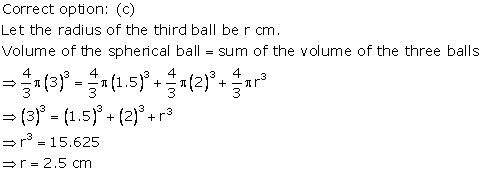
Solution 68

Solution 69

Solution 70
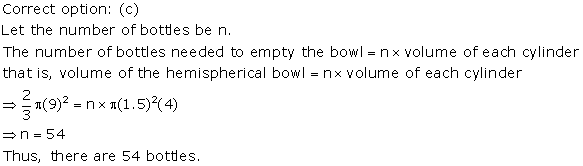
Solution 71

Solution 72

Solution 73

Volume and Surface Area of Solids Exercise Ex. 15C
Solution 1
Radius of a cone, r = 5.25 cm
Slant height of a cone, l = 10 cm
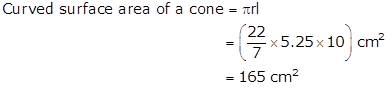
Solution 2
Radius of a cone, r = 12 m
Slant height of a cone, l = 21 cm
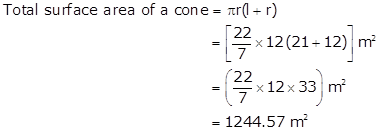
Solution 3
Radius of a conical cap, r = 7 cm
Height of a conical cap, h = 24 cm
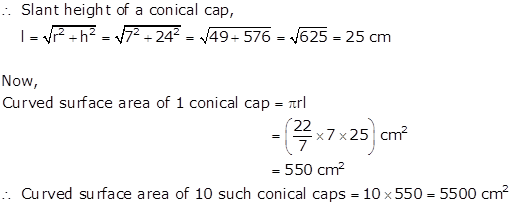
Thus, 5500 cm2 sheet will be required to make 10 caps.
Solution 4
Let r be the radius of a cone.
Slant height of a cone, l = 14 cm
Curved surface area of a cone = 308 cm2
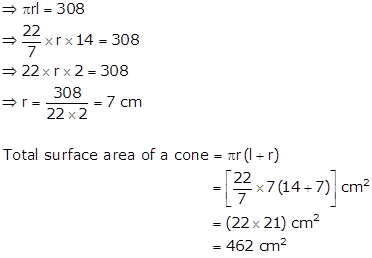
Solution 5
Radius of a cone, r = 7 m
Slant height of a cone, l = 25 m
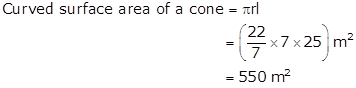
Cost of whitewashing = Rs. 12 per m2
⇒ Cost of whitewashing 550 m2 area = Rs. (12 × 550) = Rs. 6600
Solution 6
Radius of a conical tent, r = 24 m
Height of a conical tent, h = 10 m
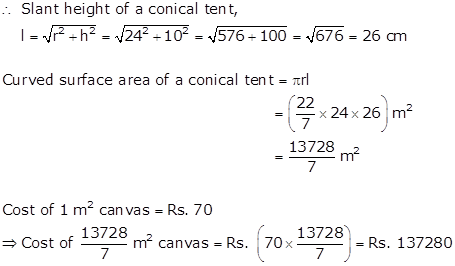
Solution 7
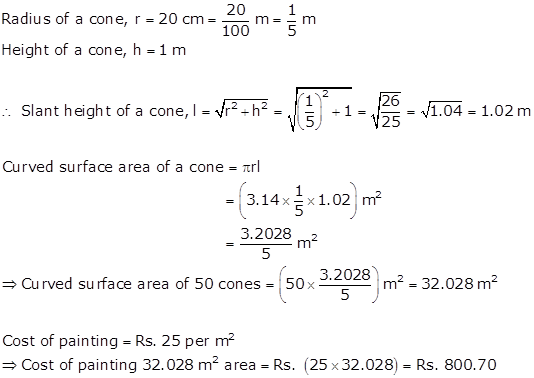
Solution 8
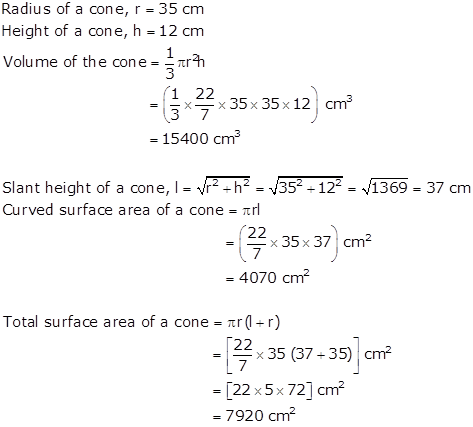
Solution 9
Solution 10
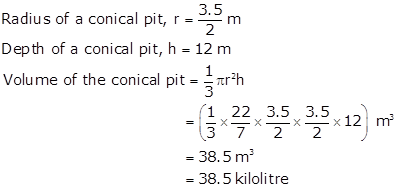
Solution 11
Radius of a conical heap, r = 4.5 m
Height of a conical tent, h = 3.5 m
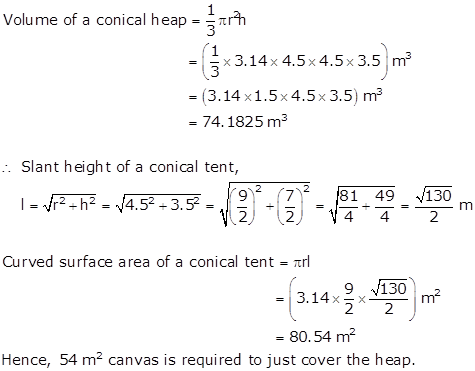
Solution 12
Radius of a conical tent, r = 7 m
Area of canvas used in making conical tent = (551 - 1) m2 = 550 m2
⇒ Curved surface area of a conical tent = 550 m2
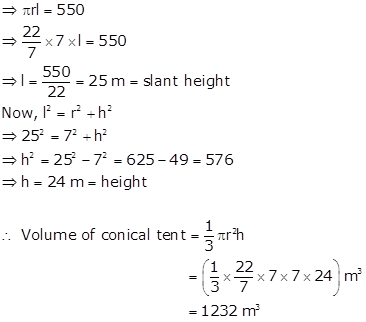
Solution 13
Solution 14
Solution 15
Solution 16
Solution 17
Solution 18
Solution 19
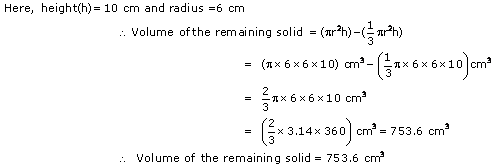
Solution 20
Solution 21

Curved surface area of the tent = Area of the cloth = 165 m2
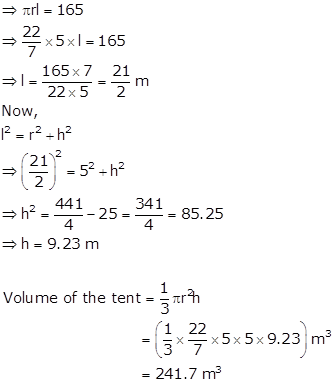
Volume and Surface Area of Solids Exercise Ex. 15A
Solution 1(iv)
Length = 24 m, breadth = 25 cm =0.25 m, height = 6m.
![]() Volume of cuboid= l x b x h
Volume of cuboid= l x b x h
= (24 x 0.25 x 6) m3.
= 36 m3.
![]() Lateral surface area= 2(l + b) x h
Lateral surface area= 2(l + b) x h
= [2(24 +0.25) x 6] m2
= (2 x 24.25 x 6) m2
= 291 m2.
![]() Total surface area =2(lb+ bh + lh)
Total surface area =2(lb+ bh + lh)
=2(24 x 0.25+0.25x 6 +24 x 6) m2
= 2(6+1.5+144) m2
= (2 x151.5) m2=303 m2.
Solution 1(iii)
Length = 15 m, breadth = 6m and height = 5 dm = 0.5 m
![]() Volume of a cuboid = l x b x h
Volume of a cuboid = l x b x h
= (15 x 6 x 0.5) m3=45 m3.
![]() Lateral surface area = 2(l + b) x h
Lateral surface area = 2(l + b) x h
= [2(15 + 6) x 0.5] m2
= (2 x 21x0.5) m2=21 m2
![]() Total surface area =2(lb+ bh + lh)
Total surface area =2(lb+ bh + lh)
= 2(15 x 6 +6 x 0.5+ 15 x 0.5) m2
= 2(90+3+7.5) m2
= (2 x 100.5) m2
=201 m2
Solution 1(ii)
Length 26 m, breadth =14 m and height =6.5 m
![]() Volume of a cuboid= l x b x h
Volume of a cuboid= l x b x h
= (26 x 14 x 6.5) m3
= 2366 m3
![]() Lateral surface area of a cuboid =2 (l + b) x h
Lateral surface area of a cuboid =2 (l + b) x h
= [2(26+14) x 6.5] m2
= (2 x 40 x 6.5) m2
= 520 m2
![]() Total surface area= 2(lb+ bh + lh)
Total surface area= 2(lb+ bh + lh)
= 2(26 x 14+14 x6.5 +26 x6.5)
= 2 (364+91+169) m2
= (2 x 624) m2= 1248 m2.
Solution 1(i)
length =12cm, breadth = 8 cm and height = 4.5 cm
![]() Volume of cuboid = l x b x h
Volume of cuboid = l x b x h
= (12 x 8 x 4.5) cm3= 432 cm3
![]() Lateral surface area of a cuboid = 2(l + b) x h
Lateral surface area of a cuboid = 2(l + b) x h
= [2(12 + 8) x 4.5] cm2
= (2 x 20 x 4.5) cm2 = 180 cm2
![]() Total surface area cuboid = 2(lb +b h+ l h)
Total surface area cuboid = 2(lb +b h+ l h)
= 2(12 x 8 + 8 x 4.5 + 12 x 4.5) cm2
= 2(96 +36 +54) cm2
= (2 x186) cm2
= 372 cm2
Solution 2
For a matchbox,
Length = 4 cm
Breadth = 2.5 cm
Height = 1.5 cm
Volume of one matchbox = Volume of cuboid
= Length × Breadth × Height
= (4 × 2.5 × 1.5) cm3
= 15 cm3
Hence, volume of 12 such matchboxes = 12 × 15 = 180 cm3
Solution 3
For a cuboidal water tank,
Length = 6 m
Breadth = 5 m
Height = 4.5 m
Now,
Volume of a cuboidal water tank = Length × Breadth × Height
= (6 × 5 × 4.5) m3
= 135 m3
= 135 × 1000 litres
= 135000 litres
Thus, a tank can hold 135000 litres of water.
Solution 4
For a cuboidal water tank,
Length = 10 m
Breadth = 2.5 m
Volume = 50000 litres = 50 m3
Now,
Volume of a cuboidal tank = Length × Breadth × Height
⇒ 50 = 10 × 2.5 × Height
⇒ Height = 2 m = Depth
Thus, the depth of a tank is 2 m.
Solution 5
For a godown,
Length = 40 m
Breadth = 25 m
Height = 15 m
Volume of a godown = Length × Breadth × Height
= (40 × 25 × 15) m3
For each wooden crate,
Length = 1.5 m
Breadth = 1.25 m
Height = 0.5 m
Volume of each wooden crate = Length × Breadth × Height
= (1.5 × 1.25 × 0.5) m3
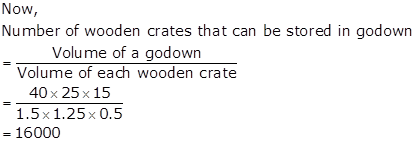
Solution 6
Solution 7
Solution 8
Length of Cistern = 8 m
Breadth of Cistern = 6 m
And Height (depth) of Cistern =2.5 m
![]() Capacity of the Cistern = Volume of cistern
Capacity of the Cistern = Volume of cistern
![]() Volume of Cistern = (l x b x h)
Volume of Cistern = (l x b x h)
= (8 x 6 x2.5) m3
=120 m3
Area of the iron sheet required = Total surface area of the cistem.
![]() Total surface area = 2(lb +bh +lh)
Total surface area = 2(lb +bh +lh)
= 2(8 x 6 + 6x2.5+ 2.5x8) m2
= 2(48 + 15 + 20) m2
= (2 x 83) m2=166 m2
Solution 9
Area of four walls of the room = 2(length + breadth) × Height
= [2(9 + 8) × 6.5] m2
= (34 × 6.5) m2
= 221 m2
Area of one door = Length × Breadth = (2 × 1.5) m2 = 3 m2
Area of two windows = 2 × (Length × Breadth)
= [2 × (1.5 × 1)] m2
= (2 × 1.5) m2
= 3 m2
Area to be whitewashed
= Area of four walls of the room - Area of one door - Area of two windows
= (221 - 3 - 3) m2
= 215 m2
Cost of whitewashing = Rs. 25 per square metre
⇒ Cost of whitewashing 215 m2 = Rs. (25 × 215) = Rs. 5375
Solution 10
L
Solution 11
External length of the box = 36 cm
External breadth of the box = 25 cm
External height of the box = 16.5 cm
∴ External volume of the box = (36 × 25 × 16.5) cm3 = 14850 cm3
Internal length of the box = [36 - (1.5 × 2)] cm = 33 cm
Internal breadth of the box = [25 - (1.5 × 2)] cm = 22 cm
Internal height of the box = (16.5 - 1.5) cm = 15 cm
∴ Internal volume of the box = (33 × 22 × 15) cm3 = 10890 cm3
Thus, volume of iron used in the box
= External volume of the box - Internal volume of the box
= (14850 - 10890) cm3
= 3960 cm3
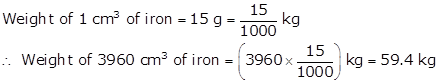
Solution 12
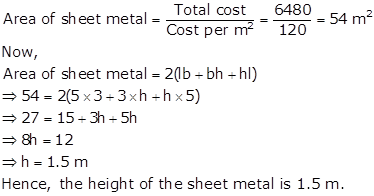
Solution 13
Solution 14
Solution 15
Solution 16
Solution 17
Solution 18
Solution 19
Solution 20
Solution 21
Solution 22
Solution 23
Solution 24
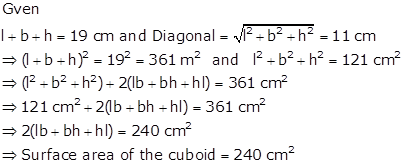
Solution 25
Let the edge of the cube = 'a' cm
Then, surface area of cube = 6a2 cm2
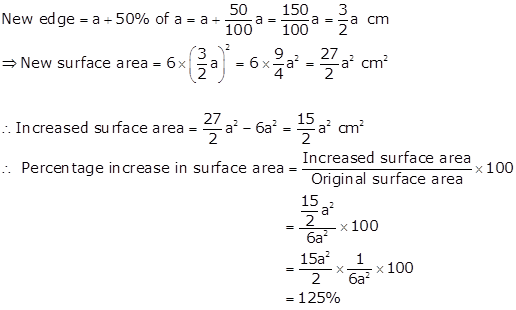
Solution 26
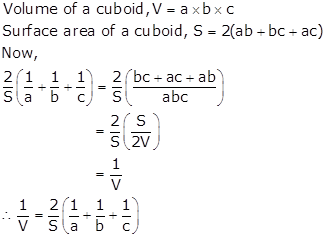
Solution 27
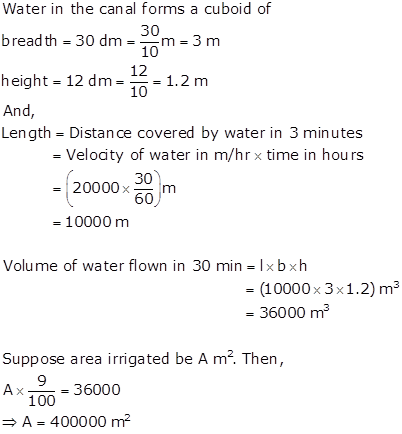
Solution 28
Volume of a cuboid = (9 × 8 × 2) m3 = 144 m3
Volume of each cube of edge 2 m = (2 m)3 = 8 m3
![]()
Volume and Surface Area of Solids Exercise Ex. 15B
Solution 1
Solution 2
Radius (r) of
cylindrical bowl =![]()
Height (h) up to which the bowl is filled with soup = 4 cm
Volume of soup in 1 bowl
= pr2h ![]() = 154 cm3
= 154 cm3
Hence, volume of soup in 250 bowls = (250 × 154) cm3 = 38500 cm3 = 38.5 litres
Thus, the hospital will have to prepare 38.5 litres of soup daily to serve 250 patients.
Solution 3
Radius (r) of pillar =
20 cm = ![]() m
m
Height (h) of pillar = 10 m
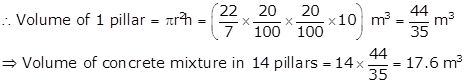
Solution 4
For a tin can of rectangular base,
Length = 5 cm
Breadth = 4 cm
Height = 15 cm
∴ Volume of a tin can = Length × Breadth × Height
= (5 × 4 × 15) cm3
= 300 cm3
For a cylinder with circular base,
Diameter
= 7 ⇒ Radius = r = ![]() cm
cm
Height = h = 10 cm
![]()
⇒ Volume of plastic cylinder is greater than volume of a tin can.
Difference in volume = (385 - 300) = 85 cm3
Thus, a plastic cylinder has more capacity that a tin can by 85 cm3.
Solution 5
Radius (r) of 1 pillar =
![]()
Height (h) of 1 pillar = 4 m
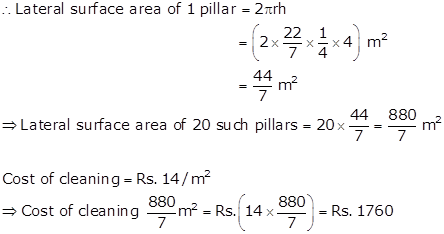
Solution 6
Curved surface area of a cylinder = 4.4 m2
Radius (r) of a cylinder = 0.7 m
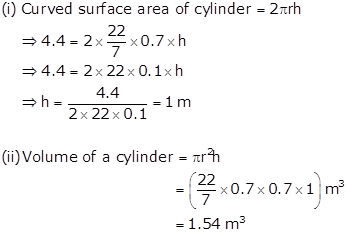
Solution 7
Lateral surface area of a cylinder = 94.2 cm2
Height (h) of a cylinder = 5 cm
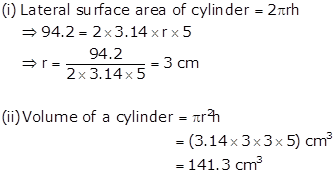
Solution 8
Volume of a cylinder = 15.4 litres = 15400 cm3
Height (h) of a cylinder = 1 m = 100 cm
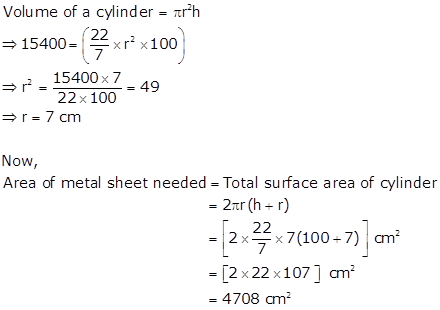
Solution 9
Internal diameter of a cylinder = 24 cm
⇒ Internal radius of a cylinder, r = 12 cm
External diameter of a cylinder = 28 cm
⇒ External radius of a cylinder, R = 14 cm
Length of the pipe, i.e height, h = 35 cm
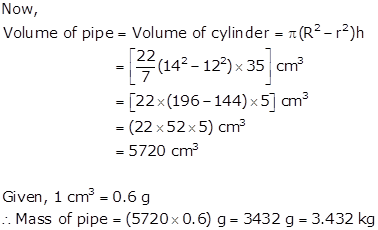
Solution 10
Diameter of a cylindrical pipe = 5 cm
⇒ Radius (r) of a cylindrical pipe = 2.5 cm
Height (h) of a cylindrical pipe = 28 m = 2800 cm
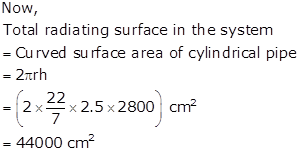
Solution 11
Solution 12
Solution 13
Solution 14
Solution 15
Solution 16
Solution 17


Solution 18
Solution 19
Solution 20
Solution 21

Solution 22
Solution 23
Diameter of a cylinder = 140 cm
⇒ Radius, r = 70 cm
Height (h) of a cylinder = 1 m = 100 cm

Solution 24
Radius (r) of cylindrical vessel = 15 cm
Height (h) of cylindrical vessel = 32 m

Radius of small cylindrical glass = 3 cm
Height of a small cylindrical glass = 8 cm
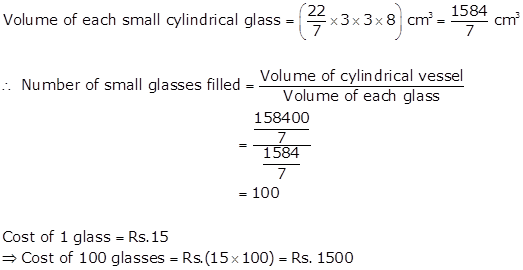
Solution 25
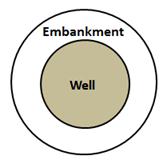
Radius of the well = 5 m
Depth of the well = 8.4 m
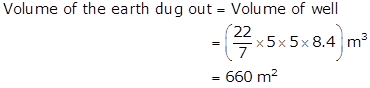
Width of the embankment = 7.5 m
External radius of the embankment, R = (5 + 7.5) m = 12.5 m
Internal radius of the embankment, r = 5 m
Area of the embankment = π (R2 - r2)

Volume of the embankment = Volume of the earth dug out = 660 m2

Solution 26
Speed of water = 30 cm/sec
∴ Volume of water that flows out of the pipe in one second
= Area of cross-section × Length of water flown in one second
= (5 × 30) cm3
= 150 cm3
Hence, volume of water that flows out of the pipe in 1 minute
= (150 × 60) cm3
= 9000 cm3
= 9 litres
Solution 27
Suppose the tank is filled in x minutes. Then,
Volume of the water that flows out through the pipe in x minutes
= Volume of the tank
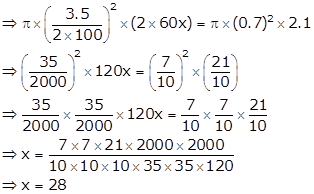
Hence, the tank will be filled in 28 minutes.
Solution 28
Let the rise in the level of water = h cm
Then,
Volume of the cylinder of height h and base radius 28 cm
= Volume of rectangular iron solid
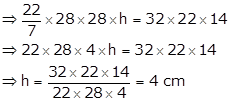
Thus, the rise in the level of water is 4 cm.
Solution 29
Radius, r = 1.5 m
Height, h = 280 m

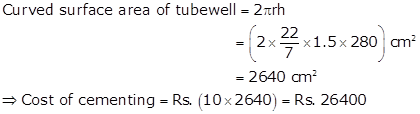
Solution 30
Let the length of the wire = 'h' metres
Then,
Volume of the wire × 8.4 g = (13.2 × 1000) g
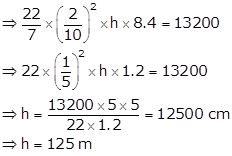
Thus, the length of the wire is 125 m.
Solution 31

Solution 32
Let R cm and r cm be the outer and inner radii of the cylindrical tube.
We have, length of tube = h = 14 cm
Now,
Outside surface area - Inner surface area = 88 cm2
⇒ 2πRh - 2πrh = 88
⇒ 2π(R - r)h = 88
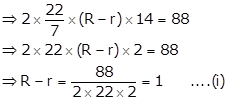
It is given that the volume of the tube = 176 cm3
⇒ External volume - Internal volume = 176 cm3
⇒ πR2h - πr2h = 176
⇒ π (R2 - r2)h = 176
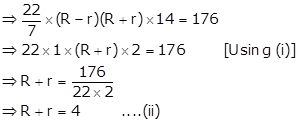
Adding (i) and (ii), we get
2R = 5
⇒ R = 2.5 cm
⇒ 2.5 - r = 1
⇒ r = 1.5 cm
Thus, the inner and outer radii of the tube are 1.5 cm and 2.5 cm respectively.
Solution 33
When the sheet is folded along its length, it forms a cylinder of height, h1 = 18 cm and perimeter of base equal to 30 cm.
Let r1 be the radius of the base and V1 be is volume.
Then,
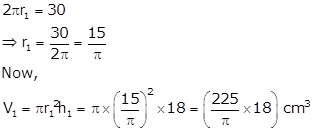
Again, when the sheet is folded along its breadth, it forms a cylinder of height, h2 = 30 cm and perimeter of base equal to 18 cm.
Let r2 be the radius of the base and V2 be is volume.
Then,
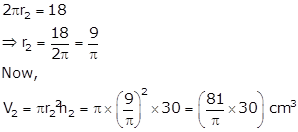
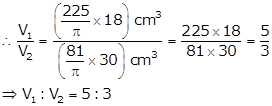
Volume and Surface Area of Solids Exercise Ex. 15D
Solution 1(iii)
Solution 1(ii)
Solution 1(i)
Solution 2
Solution 3
Solution 4
Surface area of sphere = 154 cm2
⇒ 4πr2 = 154
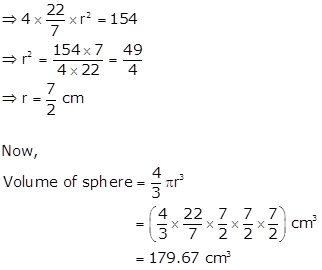
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
Solution 13
Solution 14
Solution 15

Solution 16
Solution 17
Solution 18
Solution 19
Solution 20

Solution 21

Solution 22

Solution 23
Solution 24

Solution 25
Inner radius = 5 cm
⇒ Outer radius = 5 + 0.25 = 5.25 cm
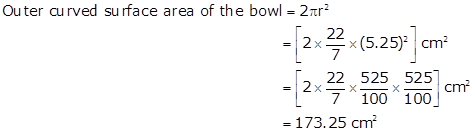
Solution 26
Inner diameter of the hemispherical bowl = 10.5 cm
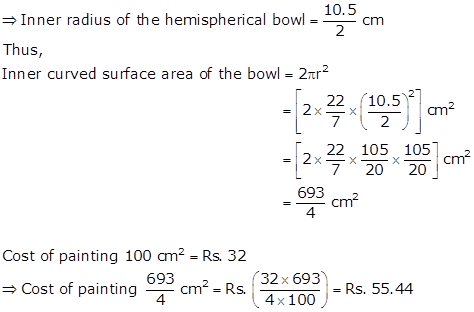
Solution 27
Let the diameter of earth = d
⇒ Radius of the earth
= ![]()
Then, diameter of moon = ![]() .
.
⇒ Radius of moon
= ![]()
Volume of moon ![]()
Volume of earth ![]()
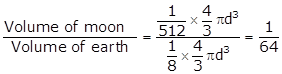
Thus, the volume of moon
is ![]() of volume of earth.
of volume of earth.
Solution 28
Volume of a solid hemisphere = Surface area of a solid hemisphere