Class 9 R S AGGARWAL AND V AGGARWAL Solutions Maths Chapter 2 - Polynomials
Polynomials Exercise MCQ
Solution 1

Solution 2
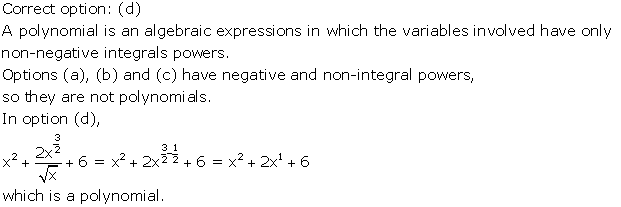
Solution 3

Solution 4

Solution 5

Solution 6
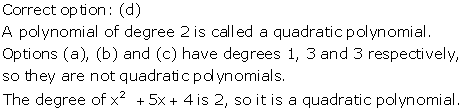
Solution 7

Solution 8

Solution 9

Solution 10

Solution 11

Solution 12
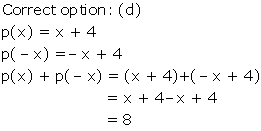
Solution 13

Solution 14
Correct option: (d)
P(x) = 5x - 4x2 + 3
⇒ p(-1) = 5(-1) - 4(-1)2 + 3 = -5 - 4 + 3 = -6
Solution 15
Correct option: (d)
Let f(x) = x51 + 51
By the remainder theorem, when f(x) is divided by (x + 1), the remainder is f(-1).
Now, f(-1) = [(-1)n + 51] = -1 + 51 = 50
Solution 16
Correct option: (c)
Let p(x) = 2x2 + kx
Since (x + 1) is a factor of p(x),
P(–1) = 0
⇒ 2(–1)2 + k(–1) = 0
⇒ 2 – k = 0
⇒ k = 2
Solution 17

Solution 18
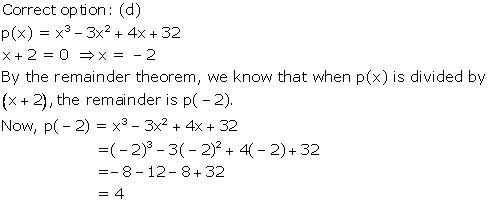
Solution 19
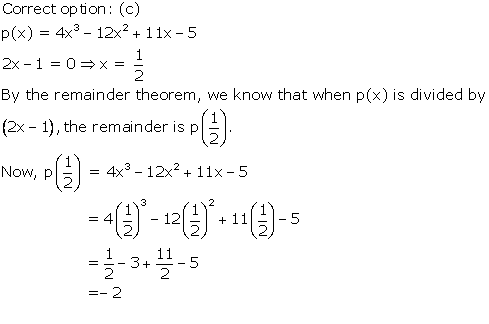
Solution 20

Solution 21

Solution 22

Solution 23
Correct option: (b)
p(x) = 2x + 5
Now, p(x) = 0
⇒ 2x + 5 = 0
⇒ 2x = -5
![]()
Solution 24

Solution 25

Solution 26
Correct option: (c)
p(x) = 2x2 + 7x - 4
Now, p(x) = 0
⇒ 2x2 + 7x - 4 = 0
⇒ 2x2 + 8x - x - 4 = 0
⇒ 2x(x + 4) - 1(x + 4) = 0
⇒ (x + 4)(2x - 1) = 0
⇒ x + 4 = 0 and 2x - 1 = 0
⇒ x = -4 and x = ![]()
Solution 27

Solution 28

Solution 29

Solution 30

Solution 31
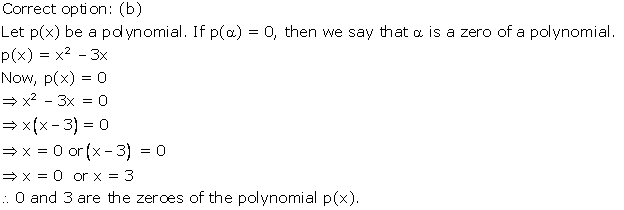
Solution 32
Correct option: (d)
p(x) = 3x2 - 1
Now, p(x) = 0
⇒ 3x2 - 1 = 0
⇒ 3x2 = 1

Polynomials Exercise Ex. 2A
Solution 1(v)
It is a polynomial, Degree = 2.
Solution 1(vi)
It is not a polynomial.
Solution 1(vii)
It is a polynomial, Degree = 0.
Solution 1(viii)
It is a polynomial, Degree = 0.
Solution 1(i)
![]()
The given expression is an expression having only non-negative integral powers of x. So, it is a polynomial.
The highest power of x is 5. So, it is a polynomial of degree 5.
Solution 1(ii)
![]()
The given expression is an expression having only non-negative integral powers of y. So, it is a polynomial.
The highest power of y is 3. So, it is a polynomial of degree 3.
Solution 1(iii)
![]()
The given expression is an expression having only non-negative integral powers of t. So, it is a polynomial.
The highest power of t is 2. So, it is a polynomial of degree 2.
Solution 1(iv)
X100 - 1
The given expression is an expression having only non-negative integral powers of x. So, it is a polynomial.
The highest power of x is 100. So, it is a polynomial of degree 100.
Solution 1(ix)
![]()
The given expression can be written as ![]()
It contains a term having negative integral power of x. So, it is not a polynomial.
Solution 1(x)
![]()
The given expression is an expression having only non-negative integral powers of x. So, it is a polynomial.
The highest power of x is 2. So, it is a polynomial of degree 2.
Solution 1(xi)
![]()
The given expression can be written as 2x-2.
It contains a term having negative integral power of x. So, it is not a polynomial.
Solution 1(xii)
![]()
The given expression contains a term containing x1/2, where ½ is not a non-negative integer.
So, it is not a polynomial.
Solution 1(xiii)
![]()
The given expression is an expression having only non-negative integral powers of x. So, it is a polynomial.
The highest power of x is 2. So, it is a polynomial of degree 2.
Solution 1(xiv)
x4 - x3/2 + x - 3
The given expression contains a term containing x3/2, where 3/2 is not a non-negative integer.
So, it is not a polynomial.
Solution 1(xv)
![]()
The given expression can be written as 2x3 + 3x2 + x1/2 - 1.
The given expression contains a term containing x1/2, where ½ is not a non-negative integer.
So, it is not a polynomial.
Solution 2(i)
-7 + x
The degree of a given polynomial is 1.
Hence, it is a linear polynomial.
Solution 2(ii)
6y
The degree of a given polynomial is 1.
Hence, it is a linear polynomial.
Solution 2(iii)
-z3
The degree of a given polynomial is 3.
Hence, it is a cubic polynomial.
Solution 2(iv)
1 - y - y3
The degree of a given polynomial is 3.
Hence, it is a cubic polynomial.
Solution 2(v)
x - x3 + x4
The degree of a given polynomial is 4.
Hence, it is a quartic polynomial.
Solution 2(vi)
1 + x + x2
The degree of a given polynomial is 2.
Hence, it is a quadratic polynomial.
Solution 2(vii)
-6x2
The degree of a given polynomial is 2.
Hence, it is a quadratic polynomial.
Solution 2(viii)
-13
The given polynomial contains only one term namely constant.
Hence, it is a constant polynomial.
Solution 2(ix)
-p
The degree of a given polynomial is 1.
Hence, it is a linear polynomial.
Solution 3(i)
The coefficient of x3 in x + 3x2 - 5x3 + x4 is -5.
Solution 3(ii)
The coefficient of x in ![]() .
.
Solution 3(iii)
The given polynomial can be written as x3 + 0x2 + 2x - 3.
Hence, the coefficient of x2 in 2x - 3 + x3 is 0.
Solution 3(iv)
The coefficient of x in ![]() .
.
Solution 3(v)
The constant term in ![]() .
.
Solution 4(i)
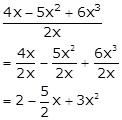
Hence, the degree of a given polynomial is 2.
Solution 4(ii)
y2(y - y3)
= y3 - y5
Hence, the degree of a given polynomial is 5.
Solution 4(iii)
(3x - 2)(2x3 + 3x2)
= 6x4 + 9x3 - 4x3 - 6x2
= 6x4 + 5x3 - 6x2
Hence, the degree of a given polynomial is 4.
Solution 4(iv)
![]()
The degree of a given polynomial is 1.
Solution 4(v)
-8
This is a constant polynomial.
The degree of a non-zero constant polynomial is zero.
Solution 4(vi)
x-2(x4 + x2)
= x-2.x2(x2 + 1)
= x0 (x2 + 1)
= x2 + 1
Hence, the degree of a given polynomial is 2.
Solution 5(i)
Example of a monomial of degree 5:
3x5
Solution 5(ii)
Example of a binomial of degree 8:
x - 6x8
Solution 5(iii)
Example of a trinomial of degree 4:
7 + 2y + y4
Solution 5(iv)
Example of a monomial of degree 0:
7
Solution 6(i)
x - 2x2 + 8 + 5x3 in standard form:
5x3 - 2x2 + x + 8
Solution 6(ii)
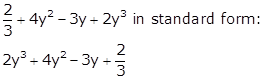
Solution 6(iii)
6x3 + 2x - x5 - 3x2 in standard form:
-x5 + 6x3 - 3x2 + 2x
Solution 6(iv)
2 + t - 3t3 + t4 - t2 in standard form:
t4 - 3t3 - t2 + t + 2
Polynomials Exercise Ex. 2B
Solution 1
p(x) = 5 - 4x + 2x2
(i) p(0) = 5 - 4 ![]() 0 + 2
0 + 2 ![]() 02 = 5
02 = 5
(ii) p(3) = 5 - 4 ![]() 3 + 2
3 + 2 ![]() 32
32
= 5 - 12 + 18
= 23 - 12 = 11
(iii) p(-2) = 5 - 4(-2) + 2 (-2)2
= 5 + 8 + 8 = 21
Solution 2
p(y) = 4 + 3y - y2 + 5y3
(i) p(0) = 4 + 3 ![]() 0 - 02 + 5
0 - 02 + 5 ![]() 03
03
= 4 + 0 - 0 + 0 = 4
(ii) p(2) = 4 + 3 ![]() 2 - 22 + 5
2 - 22 + 5 ![]() 23
23
= 4 + 6 - 4 + 40
= 10 - 4 + 40 = 46
(iii) p(-1) = 4 + 3(-1) - (-1)2 + 5(-1)3
= 4 - 3 - 1 - 5 = -5
Solution 3
f(t) = 4t2 - 3t + 6
(i) f(0) = 4 ![]() 02 - 3
02 - 3 ![]() 0 + 6
0 + 6
= 0 - 0 + 6 = 6
(ii) f(4) = 4(4)2 - 3 ![]() 4 + 6
4 + 6
= 64 - 12 + 6 = 58
(iii) f(-5) = 4(-5)2 - 3(-5) + 6
= 100 + 15 + 6 = 121
Solution 4
p(x) = x3 - 3x2 + 2x
Thus, we have
p(0) = 03 - 3(0)2 + 2(0) = 0
p(1) = 13 - 3(1)2 + 2(1) = 1 - 3 + 2 = 0
p(2) = 23 - 3(2)2 + 2(2) = 8 - 12 + 4 = 0
Hence, 0, 1 and 2 are the zeros of the polynomial p(x) = x3 - 3x2 + 2x.
Solution 5
p(x) = x3 + x2 - 9x - 9
Thus, we have
p(0) = 03 + 02 - 9(0) - 9 = -9
p(3) = 33 + 32 - 9(3) - 9 = 27 + 9 - 27 - 9 = 0
p(-3) = (-3)3 + (-3)2 - 9(-3) - 9 = -27 + 9 + 27 - 9 = 0
p(-1) = (-1)3 + (-1)2 - 9(-1) - 9 = -1 + 1 + 9 - 9 = 0
Hence, 0, 3 and -3 are the zeros of p(x).
Now, 0 is not a zero of p(x) since p(0) ≠ 0.
Solution 6(i)
p(x) = x - 4
Then, p(4) = 4 - 4 = 0
![]() 4 is a zero of the polynomial p(x).
4 is a zero of the polynomial p(x).
Solution 6(ii)
p(x) = x - 3
Then,p(-3) = -3 - 3 = -6
![]() -3 is not a zero of the polynomial p(x).
-3 is not a zero of the polynomial p(x).
Solution 6(iii)
p(y) = 2y + 1
Then, ![]()
![]() is a zero of the polynomial p(y).
is a zero of the polynomial p(y).
Solution 6(iv)
p(x) = 2 - 5x
Then, ![]()
![]() is a zero of the polynomial p(x).
is a zero of the polynomial p(x).
Solution 7(i)
p(x) = (x - 1) (x - 2)
Then,p(1)= (1 - 1) (1 - 2) = 0 ![]() -1 = 0
-1 = 0
![]() 1 is a zero of the polynomial p(x).
1 is a zero of the polynomial p(x).
Also, p(2) = (2 - 1)(2 - 2) = 1 ![]() 0 = 0
0 = 0
![]() 2 is a zero of the polynomial p(x).
2 is a zero of the polynomial p(x).
Hence,1 and 2 are the zeroes of the polynomial p(x).
Solution 7(ii)
p(x) = x2 + x - 6
Then, p(2) = 22 + 2 - 6
= 4 + 2 - 6
= 6 - 6 = 0
![]() 2 is a zero of the polynomial p(x).
2 is a zero of the polynomial p(x).
Also, p(-3) = (-3)2 - 3 - 6
= 9 - 3 - 6 = 0
![]() -3 is a zero of the polynomial p(x).
-3 is a zero of the polynomial p(x).
Hence, 2 and -3 are the zeroes of the polynomial p(x).
Solution 7(iii)
p(x) = x2 - 3x.
Then,p(0) = 02 - 3 ![]() 0 = 0
0 = 0
p(3) = (3)2- 3 ![]() 3 = 9 - 9 = 0
3 = 9 - 9 = 0
![]() 0 and 3 are the zeroes of the polynomial p(x).
0 and 3 are the zeroes of the polynomial p(x).
Solution 8(i)
p(x) = 0
![]() x - 5 = 0
x - 5 = 0
![]() x = 5
x = 5
![]() 5 is the zero of the polynomial p(x).
5 is the zero of the polynomial p(x).
Solution 8(ii)
q(x) = 0
![]() x + 4 = 0
x + 4 = 0
![]() x= -4
x= -4
![]() -4 is the zero of the polynomial q(x).
-4 is the zero of the polynomial q(x).
Solution 8(iv)
f(x) = 0
![]() 3x + 1= 0
3x + 1= 0
![]() 3x=-1
3x=-1
![]() x =
x =![]()
![]() x =
x =![]() is the zero of the polynomial f(x).
is the zero of the polynomial f(x).
Solution 8(v)
g(x) = 0
![]() 5 - 4x = 0
5 - 4x = 0
![]() -4x = -5
-4x = -5
![]() x =
x =![]()
![]() x =
x = ![]() is the zero of the polynomial g(x).
is the zero of the polynomial g(x).
Solution 8(vii)
p(x) = 0
![]() ax = 0
ax = 0
![]() x = 0
x = 0
![]() 0 is the zero of the polynomial p(x).
0 is the zero of the polynomial p(x).
Solution 8(viii)
q(x) = 0
![]() 4x = 0
4x = 0
![]() x = 0
x = 0
![]() 0 is the zero of the polynomial q(x).
0 is the zero of the polynomial q(x).
Solution 8(iii)
r(x) = 2x + 5
Now, r(x) = 0
⇒ 2x + 5 = 0
⇒ 2x = -5
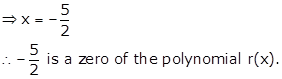
Solution 8(vi)
h(x) = 6x - 2
Now, h(x) = 0
⇒ 6x - 2 = 0
⇒ 6x = 2
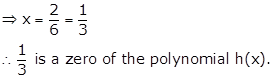
Solution 9
f(x) = 2x3 - 5x2 + ax + b
Now, 2 is a zero of f(x).
⇒ f(2) = 0
⇒ 2(2)3 - 5(2)2 + a(2) + b = 0
⇒ 16 - 20 + 2a + b = 0
⇒ 2a + b - 4 = 0 ….(i)
Also, 0 is a zero of f(x).
⇒ f(0) = 0
⇒ 2(0)3 - 5(0)2 + a(0) + b = 0
⇒ 0 - 0 + 0 + b = 0
⇒ b = 0
Substituting b = 0 in (i), we get
2a + 0 - 4 = 0
⇒ 2a = 4
⇒ a = 2
Thus, a = 2 and b = 0.
Polynomials Exercise Ex. 2D
Solution 1
f(x) = (x3 - 8)
By the Factor Theorem, (x - 2) will be a factor of f(x) if f(2) = 0.
Here, f(2) = (2)3 - 8
= 8 - 8 = 0
![]() (x - 2) is a factor of (x3 - 8).
(x - 2) is a factor of (x3 - 8).
Solution 2
f(x) = (2x3 + 7x2 - 24x - 45)
By the Factor Theorem, (x - 3) will be a factor of f(x) if f(3) = 0.
Here, f(3) = 2 ![]() 33 + 7
33 + 7 ![]() 32 - 24
32 - 24 ![]() 3 - 45
3 - 45
= 54 + 63 - 72 - 45
= 117 - 117 = 0
![]() (x - 3) is a factor of (2x3 + 7x2 - 24x - 45).
(x - 3) is a factor of (2x3 + 7x2 - 24x - 45).
Solution 3
f(x) = (2x4 + 9x3 + 6x2 - 11x - 6)
By the Factor Theorem, (x - 1) will be a factor of f(x) if f(1) = 0.
Here, f(1) = 2 ![]() 14 + 9
14 + 9 ![]() 13 + 6
13 + 6 ![]() 12 - 11
12 - 11 ![]() 1 - 6
1 - 6
= 2 + 9 + 6 - 11 - 6
= 17 - 17 = 0
![]() (x - 1) is factor of (2x4 + 9x3 + 6x2 - 11x - 6).
(x - 1) is factor of (2x4 + 9x3 + 6x2 - 11x - 6).
Solution 4
f(x) = (x4 - x2 - 12)
By the Factor Theorem, (x + 2) will be a factor of f(x) if f(-2) = 0.
Here, f(-2) = (-2)4 - (-2)2 - 12
= 16 - 4 - 12
= 16 - 16 = 0
![]() (x + 2) is a factor of (x4 - x2 - 12).
(x + 2) is a factor of (x4 - x2 - 12).
Solution 5
By the factor theorem, g(x) = x + 3 will be a factor of p(x) if p(-3) = 0.
Now, p(x) = 69 + 11x - x2 + x3
⇒ p(-3) = 69 + 11(-3) - (-3)2 + (-3)3
= 69 - 33 - 9 - 27
= 0
Hence, g(x) = x + 3 is a factor of the given polynomial p(x).
Solution 6
f(x) = 2x3 + 9x2 - 11x - 30
By the Factor Theorem, (x + 5) will be a factor of f(x) if f(-5) = 0.
Here, f(-5) = 2(-5)3 + 9(-5)2 - 11(-5) - 30
= -250 + 225 + 55 - 30
= -280 + 280 = 0
![]() (x + 5) is a factor of (2x3 + 9x2 - 11x - 30).
(x + 5) is a factor of (2x3 + 9x2 - 11x - 30).
Solution 7
f(x) = (2x4 + x3 - 8x2 - x + 6)
By the Factor Theorem, (x - a) will be a factor of f(x) if f(a) = 0.
Here, 2x - 3 = 0 ![]() x =
x = ![]()
![]()
![]()
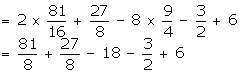
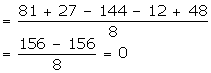
![]() is a factor of
is a factor of ![]() .
.
Solution 8
By
the factor theorem, g(x) = 3x - 2 will be a factor of p(x) if ![]() = 0.
= 0.
Now, p(x) = 3x3 + x2 - 20x + 12
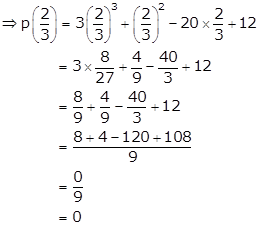
Hence, g(x) = 3x - 2 is a factor of the given polynomial p(x).
Solution 9
f(x) = ![]()
By the Factor Theorem, (x - a) will be a factor of f(x) if f(a) = 0.
Here, ![]()
= 14 - 8 - 6
= 14 - 14 = 0
![]()
Solution 10
f(x) = ![]()
By the Factor Theorem, (x - a) will be a factor of f(x) if f(a) = 0.
Here,

![]()
Solution 11
Let q(p) = (p10 - 1) and f(p) = (p11 - 1)
By the factor theorem, (p - 1) will be a factor of q(p) and f(p) if q(1) and f(1) = 0.
Now, q(p) = p10 - 1
⇒ q(1) = 110 - 1 = 1 - 1 = 0
Hence, (p - 1) is a factor of p10 - 1.
And, f(p) = p11 - 1
⇒ f(1) = 111 - 1 = 1 - 1 = 0
Hence, (p - 1) is also a factor of p11 - 1.
Solution 12
f(x) = (2x3 + 9x2 + x + k)
x - 1 = 0 ![]() x = 1
x = 1
![]() f(1) = 2
f(1) = 2 ![]() 13 + 9
13 + 9 ![]() 12 + 1 + k
12 + 1 + k
= 2 + 9 + 1 + k
= 12 + k
Given that (x - 1) is a factor of f(x).
By the Factor Theorem, (x - a) will be a factor of f(x) if f(a) = 0 and therefore f(1) = 0.
![]() f(1) = 12 + k = 0
f(1) = 12 + k = 0
![]() k = -12.
k = -12.
Solution 13
f(x) = (2x3 - 3x2 - 18x + a)
x - 4 = 0 ![]() x = 4
x = 4
![]() f(4) = 2(4)3 - 3(4)2 - 18
f(4) = 2(4)3 - 3(4)2 - 18 ![]() 4 + a
4 + a
= 128 - 48 - 72 + a
= 128 - 120 + a
= 8 + a
Given that (x - 4) is a factor of f(x).
By the Factor Theorem, (x - a) will be a factor of f(x) if f(a) = 0 and therefore f(4) = 0.
![]() f(4) = 8 + a = 0
f(4) = 8 + a = 0
![]() a = -8
a = -8
Solution 14
Let p(x) = ax3 + x2 - 2x + 4a - 9
It is given that (x + 1) is a factor of p(x).
⇒ p(-1) = 0
⇒ a(-1)3 + (-1)2 - 2(-1) + 4a - 9 = 0
⇒ -a + 1 + 2 + 4a - 9 = 0
⇒ 3a - 6 = 0
⇒ 3a = 6
⇒ a = 2
Solution 15
Let p(x) = x5 - 4a2x3 + 2x + 2a + 3
It is given that (x + 2a) is a factor of p(x).
⇒ p(-2a) = 0
⇒ (-2a)5 - 4a2(-2a)3 + 2(-2a) + 2a + 3 = 0
⇒ -32a5 - 4a2(-8a3) - 4a + 2a + 3 = 0
⇒ -32a5 + 32a5 -2a + 3 = 0
⇒ 2a = 3
![]()
Solution 16
Let p(x) = 8x4 + 4x3 - 16x2 + 10x + m
It is given that (2x - 1) is a factor of p(x).
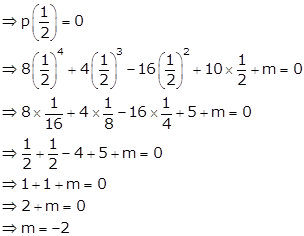
Solution 17
Let p(x) = x4 - x3 - 11x2 - x + a
It is given that p(x) is divisible by (x + 3).
⇒ (x + 3) is a factor of p(x).
⇒ p(-3) = 0
⇒ (-3)4 - (-3)3 - 11(-3)2 - (-3) + a = 0
⇒ 81 + 27 - 99 + 3 + a = 0
⇒ 12 + a = 0
⇒ a = -12
Solution 18
Let f(x) = x3 - 3x2 - 13x + 15
Now, x2 + 2x - 3 = x2 + 3x - x - 3
= x (x + 3) - 1 (x + 3)
= (x + 3) (x - 1)
Thus, f(x) will be exactly divisible by x2 + 2x - 3 = (x + 3) (x - 1) if (x + 3) and (x - 1) are both factors of f(x), so by factor theorem, we should have f(-3) = 0 and f(1) = 0.
Now, f(-3) = (-3)3 - 3 (-3)2 - 13 (-3) + 15
= -27 - 3 ![]() 9 + 39 + 15
9 + 39 + 15
= -27 - 27 + 39 + 15
= -54 + 54 = 0
And, f(1) = 13 - 3 ![]() 12 -
13
12 -
13 ![]() 1 + 15
1 + 15
= 1 - 3 - 13 + 15
= 16 - 16 = 0
![]() f(-3) = 0 and f(1) = 0
f(-3) = 0 and f(1) = 0
So, x2 + 2x - 3 divides f(x) exactly.
Solution 19
Letf(x) = (x3 + ax2 + bx + 6)
Now, by remainder theorem, f(x) when divided by (x - 3) will leave a remainder as f(3).
So, f(3) = 33 + a ![]() 32 + b
32 + b ![]() 3 + 6 = 3
3 + 6 = 3
![]() 27 + 9a + 3b + 6 = 3
27 + 9a + 3b + 6 = 3
![]() 9 a + 3b + 33 = 3
9 a + 3b + 33 = 3
![]() 9a + 3b = 3 - 33
9a + 3b = 3 - 33
![]() 9a + 3b = -30
9a + 3b = -30
![]() 3a + b = -10(i)
3a + b = -10(i)
Given that (x - 2) is a factor of f(x).
By the Factor Theorem, (x - a) will be a factor of f(x) if f(a) = 0 and therefore f(2) = 0.
![]() f(2) = 23 + a
f(2) = 23 + a ![]() 22 + b
22 + b ![]() 2 + 6 = 0
2 + 6 = 0
![]() 8 + 4a+ 2b + 6 = 0
8 + 4a+ 2b + 6 = 0
![]() 4a + 2b = -14
4a + 2b = -14
![]() 2a + b = -7(ii)
2a + b = -7(ii)
Subtracting (ii) from (i), we get,
![]() a = -3
a = -3
Substituting the value of a = -3 in (i), we get,
3(-3) + b = -10
![]() -9 + b = -10
-9 + b = -10
![]() b = -10 + 9
b = -10 + 9
![]() b = -1
b = -1
![]() a = -3 and b = -1.
a = -3 and b = -1.
Solution 20
Let f(x) = (x3 - 10x2 + ax + b), then by factor theorem
(x - 1) and (x - 2) will be factors of f(x) if f(1) = 0 and f(2) = 0.
![]() f(1) = 13 - 10
f(1) = 13 - 10 ![]() 12 + a
12 + a ![]() 1 + b = 0
1 + b = 0
![]() 1 - 10 + a + b = 0
1 - 10 + a + b = 0
![]() a + b = 9(i)
a + b = 9(i)
Andf(2) = 23 - 10 ![]() 22 + a
22 + a ![]() 2 + b = 0
2 + b = 0
![]() 8 - 40 + 2a + b = 0
8 - 40 + 2a + b = 0
![]() 2a + b = 32(ii)
2a + b = 32(ii)
Subtracting (i) from (ii), we get
a = 23
Substituting the value of a = 23 in (i), we get
23 + b = 9
![]() b = 9 - 23
b = 9 - 23
![]() b = -14
b = -14
![]() a = 23 and b = -14.
a = 23 and b = -14.
Solution 21
Letf(x)= (x4 + ax3 - 7x2 - 8x + b)
Now, x + 2 = 0 ![]() x = -2 and x + 3 = 0
x = -2 and x + 3 = 0 ![]() x = -3
x = -3
By factor theorem, (x + 2) and (x + 3) will be factors of f(x) if f(-2) = 0 and f(-3) = 0
![]() f(-2) = (-2)4 + a (-2)3 - 7 (-2)2 - 8 (-2) + b = 0
f(-2) = (-2)4 + a (-2)3 - 7 (-2)2 - 8 (-2) + b = 0
![]() 16 - 8a - 28 + 16 + b = 0
16 - 8a - 28 + 16 + b = 0
![]() -8a + b = -4
-8a + b = -4
![]() 8a - b = 4(i)
8a - b = 4(i)
And, f(-3) = (-3)4 + a (-3)3 - 7 (-3)2 - 8 (-3) + b = 0
![]() 81 - 27a - 63 + 24 + b = 0
81 - 27a - 63 + 24 + b = 0
![]() -27a + b = -42
-27a + b = -42
![]() 27a - b = 42(ii)
27a - b = 42(ii)
Subtracting (i) from (ii), we get,
19a = 38
So, a = 2
Substituting the value of a = 2 in (i), we get
8 ![]() 2 - b = 4
2 - b = 4
![]() 16 - b = 4
16 - b = 4
![]() -b = -16 + 4
-b = -16 + 4
![]() -b = -12
-b = -12
![]() b = 12
b = 12
![]() a = 2 and b = 12.
a = 2 and b = 12.
Solution 22
Let f(x) = px2 + 5x + r
Now, (x - 2) is a factor of f(x).
⇒ f(2) = 0
⇒ p(2)2 + 5(2) + r = 0
⇒ 4p + 10 + r = 0
⇒ 4p + r = -10
Also,
![]() is a factor of
f(x).
is a factor of
f(x).
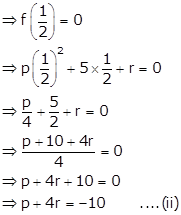
From (i) and (ii), we have
4p + r = p + 4r
⇒ 4p - p = 4r - r
⇒ 3p = 3r
⇒ p = r
Solution 23
Let f(x) = 2x4 - 5x3 + 2x2 - x + 2
and g(x) = x2 - 3x + 2
= x2 - 2x - x + 2
= x(x - 2) - 1(x - 2)
= (x - 2)(x - 1)
Clearly, (x - 2) and (x - 1) are factors of g(x).
In order to prove that f(x) is exactly divisible by g(x), it is sufficient to prove that f(x) is exactly divisible by (x - 2) and (x - 1).
Thus, we will show that (x - 2) and (x - 1) are factors of f(x).
Now,
f(2) = 2(2)4 - 5(2)3 + 2(2)2 - 2 + 2 = 32 - 40 + 8 = 0 and
f(1) = 2(1)4 - 5(1)3 + 2(1)2 - 1 + 2 = 2 - 5 + 2 - 1 + 2 = 0
Therefore, (x - 2) and (x - 1) are factors of f(x).
⇒ g(x) = (x - 2)(x - 1) is a factor of f(x).
Hence, f(x) is exactly divisible by g(x).
Solution 24
Let the required number to be added be k.
Then, p(x) = 2x4 - 5x3 + 2x2 - x - 3 + k and g(x) = x - 2
Thus, we have
p(2) = 0
⇒ 2(2)4 - 5(2)3 + 2(2)2 - 2 - 3 + k = 0
⇒ 32 - 40 + 8 - 5 + k = 0
⇒ k - 5 = 0
⇒ k = 5
Hence, the required number to be added is 5.
Solution 25
Let p(x) = x4 + 2x3 - 2x2 + 4x + 6 and q(x) = x2 + 2x - 3.
When p(x) is divided by q(x), the remainder is a linear expression in x.
So, let r(x) = ax + b be subtracted from p(x) so that p(x) - r(x) is divided by q(x).
Let f(x) = p(x) - r(x) = p(x) - (ax + b)
= (x4 + 2x3 - 2x2 + 4x + 6) - (ax + b)
= x4 + 2x3 - 2x2 + (4 - a)x + 6 - b
We have,
q(x) = x2 + 2x - 3
= x2 + 3x - x - 3
= x(x + 3) - 1(x + 3)
= (x + 3)(x - 1)
Clearly, (x + 3) and (x - 1) are factors of q(x).
Therefore, f(x) will be divisible by q(x) if (x + 3) and (x - 1) are factors of f(x).
i.e., f(-3) = 0 and f(1) = 0
Consider, f(-3) = 0
⇒ (-3)4 + 2(-3)3 - 2(-3)2 + (4 - a)(-3) + 6 - b = 0
⇒ 81 - 54 - 18 - 12 + 3a + 6 - b = 0
⇒ 3 + 3a - b = 0
⇒ 3a - b = -3 ….(i)
And, f(1) = 0
⇒ (1)4 + 2(1)3 - 2(1)2 + (4 - a)(1) + 6 - b = 0
⇒ 1 + 2 - 2 + 4 - a + 6 - b = 0
⇒ 11 - a - b = 0
⇒ -a - b = -11 ….(ii)
Subtracting (ii) from (i), we get
4a = 8
⇒ a = 2
Substituting a = 2 in (i), we get
3(2) - b = -3
⇒ 6 - b = -3
⇒ b = 9
Putting the values of a and b in r(x) = ax + b, we get
r(x) = 2x + 9
Hence, p(x) is divisible by q(x), if r(x) = 2x + 9 is subtracted from it.
Solution 26
Let f(x) = xn + an
In order to prove that (x + a) is a factor of f(x) for any odd positive integer n, it is sufficient to show that f(-a) = 0.
Now,
f(-a) = (-a)n + an
= (-1)n an + an
= [(-1)n + 1] an
= [-1 + 1] an …[n is odd ⇒ (-1)n = -1]
= 0 × an
= 0
Hence, (x + a) is a factor of xn + an for any odd positive integer n.
Polynomials Exercise Ex. 2C
Solution 1
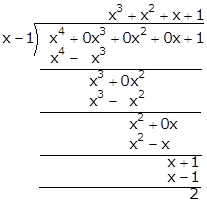
Quotient = x3 + x2 + x + 1
Remainder = 2
Verification:
f(x) = x4 + 1
Then, f(1) = 14 + 1 = 1 + 1 = 2 = Remainder
Solution 2
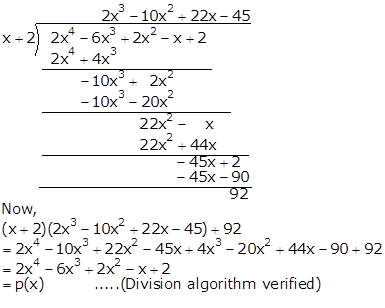
Solution 3
f(x) = x3 - 6x2 + 9x + 3
Now, x - 1 = 0 ![]() x = 1
x = 1
By the remainder theorem, we know that when f(x) is divided by (x - 1) the remainder is f(1).
Now, f(1) = 13 - 6 ![]() 12 + 9
12 + 9 ![]() 1 + 3
1 + 3
= 1 - 6 + 9 + 3
= 13 - 6 = 7
![]() The required remainder is 7.
The required remainder is 7.
Solution 4
x - 3 = 0
⇒ x = 3
By the remainder theorem, we know that when p(x) = 2x3 - 7x2 + 9x - 13 is divided by g(x) = x - 3, the remainder is g(3).
Now,
g(3) = 2(3)3 - 7(3)2 + 9(3) - 13 = 54 - 63 + 27 - 13 = 5
Hence, the required remainder is 5.
Solution 5
x - 2 = 0
⇒ x = 2
By the remainder theorem, we know that when p(x) = 3x4 - 6x2 - 8x - 2 is divided by g(x) = x - 2, the remainder is g(2).
Now,
g(2) = 3(2)4 - 6(2)2 - 8(2) - 2 = 48 - 24 - 16 - 2 = 6
Hence, the required remainder is 6.
Solution 6
2x - 3 = 0
⇒ x = ![]()
By
the remainder theorem, we know that when p(x) = 2x3 - 9x2 + x + 15 is divided by
g(x) = 2x - 3, the remainder is g![]() .
.
Now,
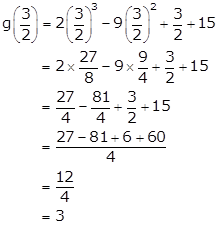
Hence, the required remainder is 3.
Solution 7
x + 1 = 0
⇒ x = -1
By the remainder theorem, we know that when p(x) = x3 - 2x2 - 8x - 1 is divided by g(x) = x + 1, the remainder is g(-1).
Now,
g(-1) = (-1)3 - 2(-1)2 - 8(-1) - 1 = -1 - 2 + 8 - 1 = 4
Hence, the required remainder is 4.
Solution 8
x + 2 = 0
⇒ x = -2
By the remainder theorem, we know that when p(x) = 2x3 + x2 - 15x - 12 is divided by g(x) = x + 2, the remainder is g(-2).
Now,
g(-2) = 2(-2)3 + (-2)2 - 15(-2) - 12 = -16 + 4 + 30 - 12 = 6
Hence, the required remainder is 6.
Solution 9
3x + 2 = 0
⇒ x = ![]()
By
the remainder theorem, we know that when p(x) = 6x3 + 13x2 + 3 is divided by
g(x) = 3x + 2, the remainder is g![]() .
.
Now,

Hence, the required remainder is 7.
Solution 10
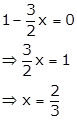
By
the remainder theorem, we know that when p(x) = x3 - 6x2 + 2x - 4 is divided by
g(x) = ![]() , the remainder is g
, the remainder is g![]() .
.
Now,
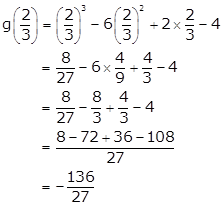
Hence,
the required remainder is ![]() .
.
Solution 11
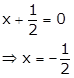
By
the remainder theorem, we know that when p(x) = 2x3 + 3x2 - 11x - 3 is divided by
g(x) = ![]() , the remainder is g
, the remainder is g![]() .
.
Now,
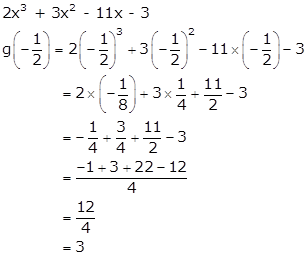
Hence, the required remainder is 3.
Solution 12
x - a = 0
⇒ x = a
By the remainder theorem, we know that when p(x) = x3 - ax2 + 6x - a is divided by g(x) = x - a, the remainder is g(a).
Now,
g(a) = (a)3 - a(a)2 + 6(a) - a = a3- a3+ 6a - a = 5a
Hence, the required remainder is 5a.
Solution 13
Let p(x) = 2x3 + x2 - ax + 2 and q(x) = 2x3 - 3x2 - 3x + a be the given polynomials.
The remainders when p(x) and q(x) are divided by (x - 2) are p(2) and q(2) respectively.
By the given condition, we have
p(2) = q(2)
⇒ 2(2)3 + (2)2 - a(2) + 2 = 2(2)3 - 3(2)2 - 3(2) + a
⇒ 16 + 4 - 2a + 2 = 16 - 12 - 6 + a
⇒ 22 - 2a = -2 + a
⇒ a + 2a = 22 + 2
⇒ 3a = 24
⇒ a = 8
Solution 14
Letf(x) = (x4 - 2x3 + 3x2 - ax + b)
![]() From the given information,
From the given information,
f(1) = 14 - 2(1)3 + 3(1)2 - a ![]() 1 + b = 5
1 + b = 5
![]() 1 - 2 + 3 - a + b = 5
1 - 2 + 3 - a + b = 5
![]() 2 - a + b = 5(i)
2 - a + b = 5(i)
And,
f(-1) = (-1)4 - 2(-1)3 + 3(-1)2 - a(-1) + b = 19
![]() 1 + 2 + 3 + a + b = 19
1 + 2 + 3 + a + b = 19
![]() 6 + a + b = 19(ii)
6 + a + b = 19(ii)
Adding (i) and (ii), we get
8 + 2b = 24
![]() 2b= 24 - 8 = 16
2b= 24 - 8 = 16
![]() b =
b = ![]()
Substituting the value of b = 8 in (i), we get
2 - a + 8 = 5
![]() -a + 10 = 5
-a + 10 = 5
![]() -a = -10 + 5
-a = -10 + 5
![]() -a = -5
-a = -5
![]() a = 5
a = 5
![]() a = 5 and b = 8
a = 5 and b = 8
f(x) = x4 - 2x3 + 3x2 - ax + b
= x4 - 2x3 + 3x2 - 5x + 8
![]() f(2) = (2)4 - 2(2)3 + 3(2)2 - 5
f(2) = (2)4 - 2(2)3 + 3(2)2 - 5 ![]() 2 + 8
2 + 8
= 16 - 16 + 12 - 10 + 8
= 20 - 10 = 10
![]() The required remainder is 10.
The required remainder is 10.
Solution 15
The polynomial p(x) will be a multiple of g(x) if g(x) divides p(x) completely.
i.e. when p(x) is divided by g(x), it does not leave any remainder.
Now, x - 2 = 0 ⇒ x = 2
Also,
p(2) = (2)3 - 5(2)2 + 4(2) - 3 = 8 - 20 + 8 - 3 = -7 ≠ 0
Thus, p(x) is not a multiple of g(x).
Solution 16
The polynomial g(x) will be a factor of p(x) if g(x) divides p(x) completely.
i.e. when p(x) is divided by g(x), it does not leave any remainder.
Now,
2x + 1 = 0 ⇒ x = ![]()
Also,
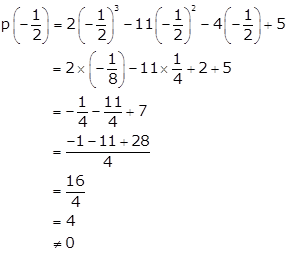
Thus, g(x) is not a factor of p(x).

