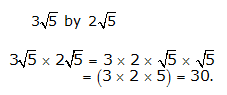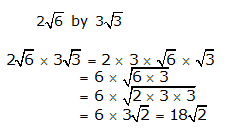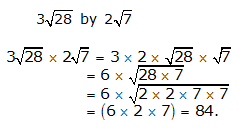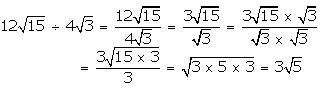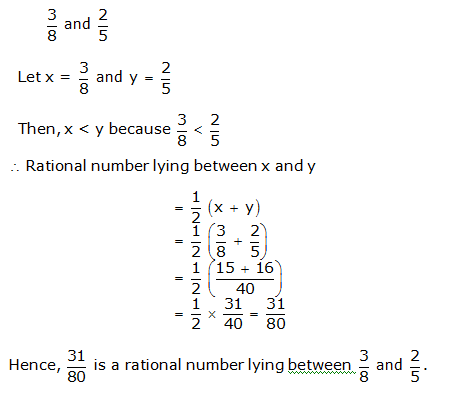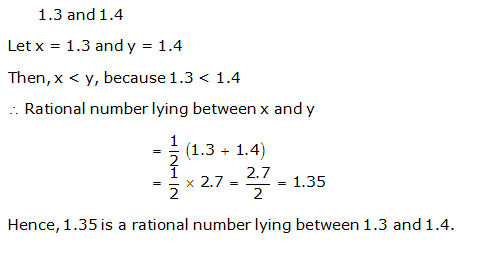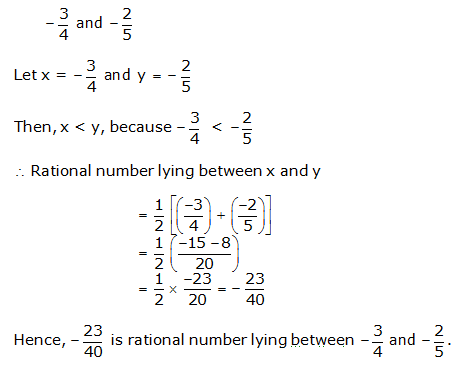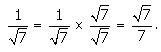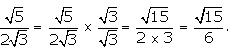Class 9 R S AGGARWAL AND V AGGARWAL Solutions Maths Chapter 1 - Number Systems
Number Systems Exercise VSAQ
Solution 1
The sum of a rational number and an irrational number is irrational.
Example: 5 + ![]() is irrational.
is irrational.
Solution 2
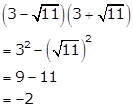
Solution 3
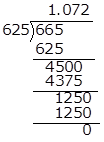
Thus, the given number will terminate after 3 decimal places.
Solution 4
(1296)0.17× (1296)0.08
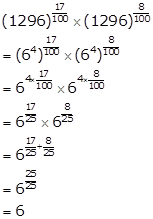
Solution 5

Solution 6
An irrational number between 5 and
6 = ![]()
Solution 7
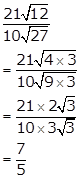
Solution 8
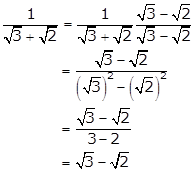
Solution 9
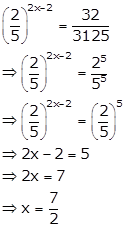
Solution 10

Solution 11
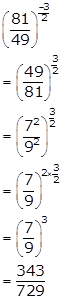
Solution 12
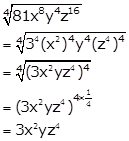
Solution 13
Given, a = 1 and b = 2
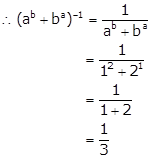
Solution 14
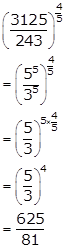
Solution 15
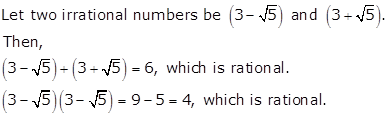
Solution 16
Yes, the product of a rational and irrational numbers is always irrational.
For example,
![]()
Solution 17
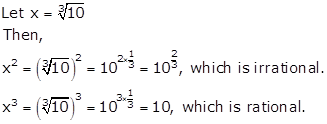
Solution 18
The reciprocal of (![]() )
)
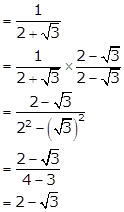
Solution 19
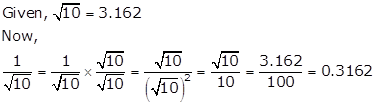
Solution 20
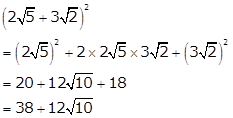
Solution 21

Solution 22

Solution 23
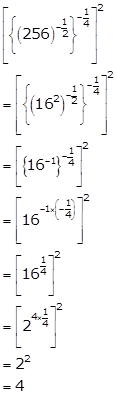
Number Systems Exercise MCQ
Solution 1
Correct option: (d)
0
can be written as ![]() where p and q are
integers and q ≠ 0.
where p and q are
integers and q ≠ 0.
Solution 2
Correct option: (a)
On a number line, 0 is a rational number that lies between -3 and 3.
Solution 3
Correct option: (c)
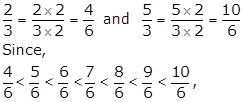
Two
rational numbers between ![]()
Solution 4
Correct option: (d)
Every point on number line represents a unique number.
Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10
Correct option: (d)
The decimal expansion of a rational number is either terminating or non-terminating recurring.
The decimal expansion of 0.5030030003…. is non-terminating non-recurring, which is not a property of a rational number.
Solution 11
Correct option: (d)
The decimal expansion of an irrational number is non-terminating non-recurring.
Hence, 3.141141114….. is an irrational number.
Solution 12
Correct option: (d)
![]()
Solution 13
Correct option: (b)
Given
two rational numbers are negative and ![]() is a positive
rational number.
is a positive
rational number.
So,
it does not lie between ![]()
Solution 14
Correct option: (c)
Π = 3.14159265359…….., which is non-terminating non-recurring.
Hence, it is an irrational number.
Solution 15
Correct option: (d)
The decimal expansion of ![]() , which is non-terminating, non-recurring.
, which is non-terminating, non-recurring.
Solution 16
Correct option: (a)
The decimal expansion of ![]() , which is non-terminating, non-recurring.
, which is non-terminating, non-recurring.
Hence, it is an irrational number.
Solution 17
Correct option: (b)
![]()
Solution 18
Correct option: (c)
The decimal expansion of ![]() , which is non-terminating, non-recurring.
, which is non-terminating, non-recurring.
Hence, it is an irrational number.
Solution 19

Solution 20

Solution 21

Solution 22
Correct option: (c)
![]()
![]()
Solution 23
Correct option: (d)
The decimal expansion of a rational number is either terminating or non-terminating recurring.
Hence, 0.853853853... is a rational number.
Solution 24
Correct option: (a)
The product of a non-zero rational number with an irrational number is always an irrational number.
Solution 25
Correct option: (b)
![]()
Solution 26

Solution 27

Solution 28

Solution 29

Solution 30
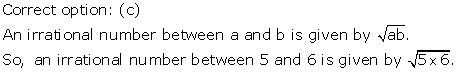
Solution 31

Solution 32
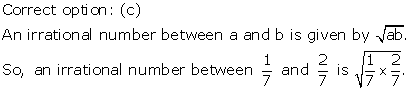
Solution 33
Correct option: (b)
Let x = ![]()
i.e. x = 0.3333…. ….(i)
⇒ 10x = 3.3333…. ….(ii)
On subtracting (i) from (ii), we get
9x = 3
![]()
Let y = ![]()
i.e. y = 0.4444…. ….(i)
⇒ 10y = 4.4444…. ….(ii)
On subtracting (i) from (ii), we get
9y = 4
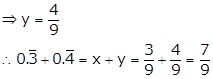
Solution 34
Correct option: (c)
Let x = ![]()
i.e. x = 2.4545…. ….(i)
⇒ 100x = 245.4545……. ….(ii)
On subtracting (i) from (ii), we get
99x = 243
![]()
Let y = ![]()
i.e. y = 0.3636…. ….(iii)
⇒ 100y = 36.3636…. ….(iv)
On subtracting (iii) from (iv), we get
99y = 36
![]()
![]()
Solution 35
Correct option: (b)
![]()
Solution 36
Correct option: (b)
![]()
Which is positive and rational number.
Solution 37
Correct option: (b)

Which is positive and rational number.
Solution 38
Correct option: (c)
![]()
Solution 39
Correct option: (a)
![]()
Solution 40
Correct option: (b)
![]()
Solution 41
Correct option: (b)
![]()
Solution 42
Correct option: (b)
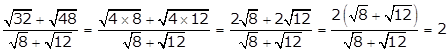
Solution 43
Correct option: (c)
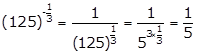
Solution 44
Correct option: (b)
![]()
Solution 45
Correct option: (d)

Solution 46
Correct option: (a)
![]()
Solution 47
Correct option: (b)
![]()
Solution 48
Correct option: (a)
![]()
Solution 49
Correct option: (c)
93 + (-3)3 - 63 = 729 - 27 - 216 = 486
Solution 50
Correct option: (b)
![]()
Solution 51
Correct option: (c)
![]()
Solution 52
Correct option: (d)
![]()
Solution 53
Correct option: (a)
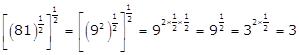
Solution 54
Correct option: (d)
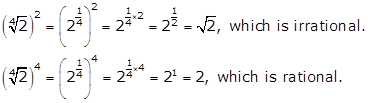
Solution 55
Correct option: (b)
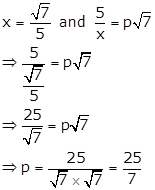
Solution 56
Correct option: (b)
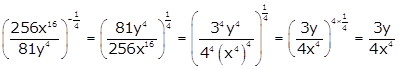
Solution 57
Correct option: (b)
xp-q⋅ xq - r⋅ xr - p
= xp - q + q - r + r - p
= x0
= 1
Solution 58
Correct option: (c)
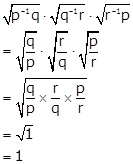
Solution 59
Correct option: (a)

Solution 60
Correct option: (d)
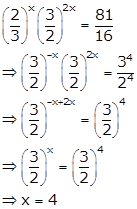
Solution 61
Correct option: (d)
(33)2 = 9x
⇒ (32)3 = (32)x
⇒ x = 3
Then 5x = 53 = 125
Solution 62
Correct option: (b)
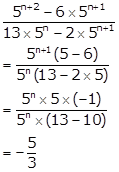
Solution 63
Correct option: (d)
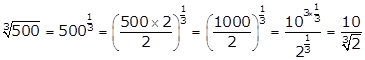
Thus, the simplest rationalisation factr of ![]()
Solution 64
Correct option: (b)
The simplest rationalisation factor of ![]() is
is ![]()
Solution 65
Correct option: (d)
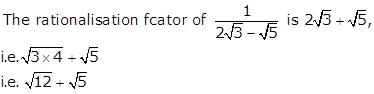
Solution 66
Correct option: (d)
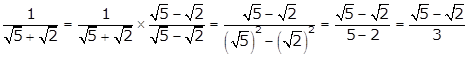
Solution 67
Correct option: (c)
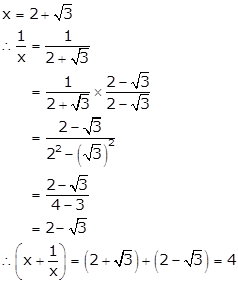
Solution 68
Correct option: (c)
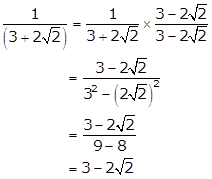
Solution 69
Correct option: (b)
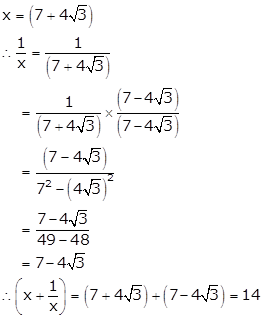
Solution 70
Correct option: (c)
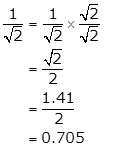
Solution 71
Correct option: (b)
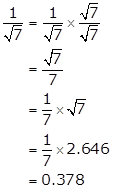
Solution 72
Correct option: (d)
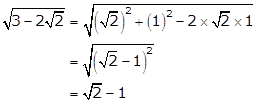
Solution 73
Correct option: (c)
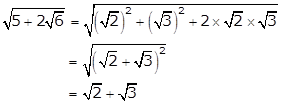
Solution 74
Correct option: (c)
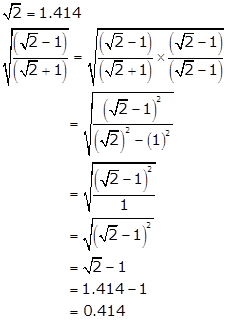
Solution 75
Correct option: (a)
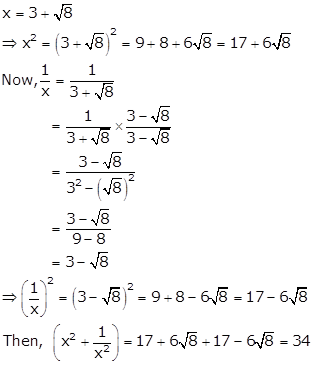
Solution 76

Solution 77

Solution 78

Solution 79

Solution 80

Solution 81

Number Systems Exercise Ex. 1B
Solution 1(i)
![]()
![]()
If the prime factors of the denominator are 2 and/or 5 then the rational number is a terminating decimal.
Since, 80 has prime factors 2 and 5, ![]() is a terminating decimal.
is a terminating decimal.
Solution 1(ii)
![]()
![]()
If the prime factors of the denominators of the fraction are other than 2 and 5, then the rational number is not a terminating decimal.
Since, 24 has prime factors 2 and 3 and 3 is different from 2 and 5,
![]() is not a terminating decimal.
is not a terminating decimal.
Solution 1(iii)
![]()
![]()
If the prime factors of the denominators of the fraction are other than 2 and 5, then the rational number is not a terminating decimal.
Since 12 has prime factors 2 and 3 and 3 is different from 2 and 5,
![]() is not a terminating decimal.
is not a terminating decimal.
Solution 1(iv)
![]()
Since the denominator of a given rational number is not of the form 2m × 2n, where m and n are whole numbers, it has non-terminating decimal.
Solution 2(i)
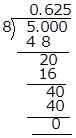
![]()
Hence, it has terminating decimal expansion.
Solution 2(ii)
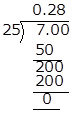
![]()
Hence, it has terminating decimal expansion.
Solution 2(iii)
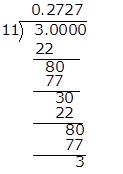
![]()
Hence, it has non-terminating recurring decimal expansion.
Solution 2(iv)
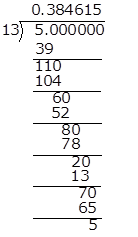
![]()
Hence, it has non-terminating recurring decimal expansion.
Solution 2(v)
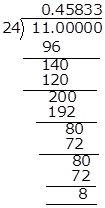
![]()
Hence, it has non-terminating recurring decimal expansion.
Solution 2(vi)
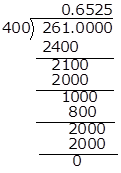
![]()
Hence, it has terminating decimal expansion.
Solution 2(vii)

![]()
Hence, it has terminating decimal expansion.
Solution 2(viii)
![]()
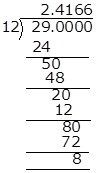
![]()
Hence, it has non-terminating recurring decimal expansion.
Solution 3(i)
Let x = ![]()
i.e. x = 0.2222…. ….(i)
⇒ 10x = 2.2222…. ….(ii)
On subtracting (i) from (ii), we get
9x = 2
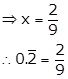
Solution 3(ii)
Let x = ![]()
i.e. x = 0.5353…. ….(i)
⇒ 100x = 53.535353…. ….(ii)
On subtracting (i) from (ii), we get
99x = 53
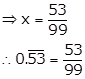
Solution 3(iii)
Let x = ![]()
i.e. x = 2.9393…. ….(i)
⇒ 100x = 293.939……. ….(ii)
On subtracting (i) from (ii), we get
99x = 291
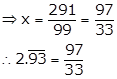
Solution 3(iv)
Let x = ![]()
i.e. x = 18.4848…. ….(i)
⇒ 100x = 1848.4848……. ….(ii)
On subtracting (i) from (ii), we get
99x = 1830
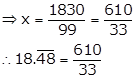
Solution 3(v)
Let x = ![]()
i.e. x = 0.235235..… ….(i)
⇒ 1000x = 235.235235……. ….(ii)
On subtracting (i) from (ii), we get
999x = 235

Solution 3(vi)
Let x = ![]()
i.e. x = 0.003232..…
⇒ 100x = 0.323232……. ….(i)
⇒ 10000x = 32.3232…. ….(ii)
On subtracting (i) from (ii), we get
9900x = 32
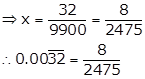
Solution 3(vii)
Let x = ![]()
i.e. x = 1.3232323..… ….(i)
⇒ 100x = 132.323232……. ….(ii)
On subtracting (i) from (ii), we get
99x = 131
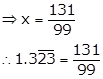
Solution 3(viii)
Let x = ![]()
i.e. x = 0.3178178..…
⇒ 10x = 3.178178…… ….(i)
⇒ 10000x = 3178.178……. ….(ii)
On subtracting (i) from (ii), we get
9990x = 3175
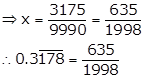
Solution 3(ix)
Let x = ![]()
i.e. x = 32.123535..…
⇒ 100x = 3212.3535…… ….(i)
⇒ 10000x = 321235.3535……. ….(ii)
On subtracting (i) from (ii), we get
9900x = 318023
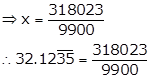
Solution 3(x)
Let x = ![]()
i.e. x = 0.40777..…
⇒ 100x = 40.777…… ….(i)
⇒ 1000x = 407.777……. ….(ii)
On subtracting (i) from (ii), we get
900x = 367

Solution 4
Let x = ![]()
i.e. x = 2.3636…. ….(i)
⇒ 100x = 236.3636……. ….(ii)
On subtracting (i) from (ii), we get
99x = 234
![]()
Let y = ![]()
i.e. y = 0.2323…. ….(iii)
⇒ 100y = 23.2323…. ….(iv)
On subtracting (iii) from (iv), we get
99y = 23
![]()
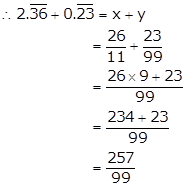
Solution 5
Let x = ![]()
i.e. x = 0.3838…. ….(i)
⇒ 100x = 38.3838…. ….(ii)
On subtracting (i) from (ii), we get
99x = 38
![]()
Let y = ![]()
i.e. y = 1.2727…. ….(iii)
⇒ 100y = 127.2727……. ….(iv)
On subtracting (iii) from (iv), we get
99y = 126
![]()
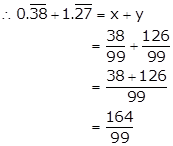
Solution 9(v)
![]()
![]()
If the prime factors of the denominator are 2 and/or 5 then the rational number is a terminating decimal.
Since 125 has prime factor 5 only
![]() is a terminating decimal.
is a terminating decimal.
Number Systems Exercise Ex. 1C
Solution 1
Irrational number: A number which cannot be expressed either as a terminating decimal or a repeating decimal is known as irrational number. Rather irrational numbers cannot be expressed in the fraction form, ![]()
For example, 0.101001000100001 is neither a terminating nor a repeating decimal and so is an irrational number.
Also, ![]() etc. are examples of irrational numbers.
etc. are examples of irrational numbers.
Solution 2(iii)
![]()
We know that, if n is a not a perfect square, then ![]() is an irrational number.
is an irrational number.
Here, ![]() is a not a perfect square number.
is a not a perfect square number.
So, ![]() is irrational.
is irrational.
Solution 2(v)
![]()
![]() is the product of a rational number
is the product of a rational number ![]() and an irrational number
and an irrational number ![]() .
.
Theorem: The product of a non-zero rational number and an irrational number is an irrational number.
Thus, by the above theorem, ![]() is an irrational number.
is an irrational number.
So, ![]() is an irrational number.
is an irrational number.
Solution 2(i)
![]()
Since quotient of a rational and an irrational is irrational, the given number is irrational.
Solution 2(ii)
![]()
Solution 2(iv)
![]()
Solution 2(vi)
The given number 4.1276 has terminating decimal expansion.
Hence, it is a rational number.
Solution 2(vii)
![]()
Since the given number has non-terminating recurring decimal expansion, it is a rational number.
Solution 2(viii)
The given number 1.232332333.... has non-terminating and non-recurring decimal expansion.
Hence, it is an irrational number.
Solution 2(ix)
The given number 3.040040004..... has non-terminating and non-recurring decimal expansion.
Hence, it is an irrational number.
Solution 2(x)
![]()
The given number 2.356565656..... has non-terminating recurring decimal expansion.
Hence, it is a rational number.
Solution 2(xi)
![]()
The given number 6.834834.... has non-terminating recurring decimal expansion.
Hence, it is a rational number.
Solution 3
We know that the sum of a rational and an irrational is irrational.
Hence, if x is rational and y is irrational, then x + y is necessarily an irrational number.
For example,
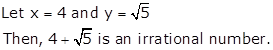
Solution 4
We know that the product of a rational and an irrational is irrational.
Hence, if a is rational and b is irrational, then ab is necessarily an irrational number.
For example,
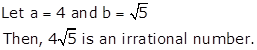
Solution 5
No, the product of two irrationals need not be an irrational.
For example,
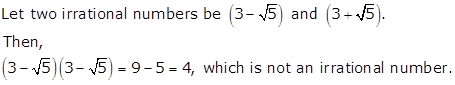
Solution 6
(i) Difference is an irrational number:
![]()
(ii) Difference is a rational number:
![]()
(iii) Sum is an irrational number:
![]()
(iv) Sum is an rational number:
![]()
(v) Product is an irrational number:
![]()
(vi) Product is a rational number:
![]()
(vii) Quotient is an irrational number:
![]()
(viii) Quotient is a rational number:
![]()
Solution 7
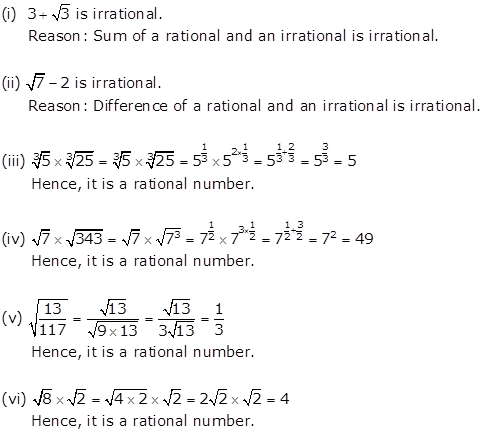
Solution 8
Rational
number between 2 and 2.5 = ![]()
Irrational
number between 2 and 2.5 = ![]()
Solution 9
There are infinite irrational
numbers between![]() .
.
We have
![]()
Hence, three irrational numbers lying between ![]() are as follows:
are as follows:
1.5010010001……., 1.6010010001…… and 1.7010010001…….
Solution 10
Since 0.5 < 0.55
Let x = 0.5, y = 0.55 and y = 2
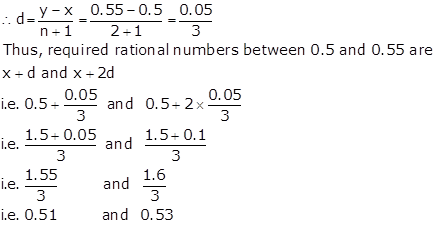
Two irrational numbers between 0.5 and 0.55 are 0.5151151115……. and 0.5353553555….
Solution 11
![]()
Thus, three different irrational
numbers between the rational numbers ![]() are as follows:
are as follows:
0.727227222….., 0.757557555….. and 0.808008000…..
Solution 12
Let a and b be two rational numbers between the numbers 0.2121121112... and 0.2020020002......
Now, 0.2020020002...... <0.2121121112...
Then, 0.2020020002...... < a < b < 0.2121121112...
![]()
Solution 13
Two irrational numbers between 0.16 and 0.17 are as follows:
0.1611161111611111611111…… and 0.169669666…….
Solution 14(i)
True
Solution 14(ii)
False
Solution 14(iii)
True
Solution 14(iv)
False
Solution 14(v)
True
Solution 14(vi)
False
Solution 14(vii)
False
Solution 14(viii)
True
Solution 14(ix)
True
Number Systems Exercise Ex. 1D
Solution 1(i)
![]()
We have:

Solution 1(ii)
![]()
We have:
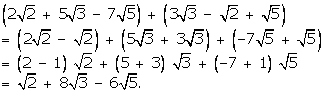
Solution 1(iii)
Solution 2(i)
Solution 2(ii)
Solution 2(iii)
Solution 2(iv)
Solution 2(v)
Solution 2(vi)
Solution 3(i)
![]()
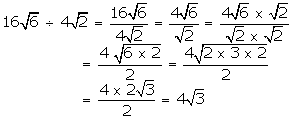
Solution 3(ii)
![]()
Solution 3(iii)
![]()
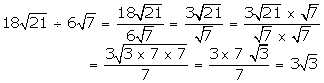
Solution 4(iii)
![]()
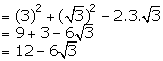
Solution 4(iv)
![]()
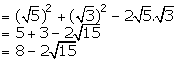
Solution 4(vi)
![]()
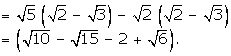
Solution 4(i)
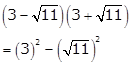
= 9 - 11
= -2
Solution 4(ii)
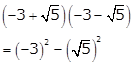
= 9 - 5
= 4
Solution 4(v)
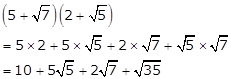
Solution 5

Solution 6(i)
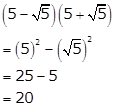
Thus, the given number is rational.
Solution 6(ii)
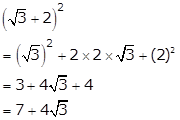
Clearly, the given number is irrational.
Solution 6(iii)
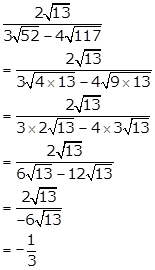
Thus, the given number is rational.
Solution 6(iv)
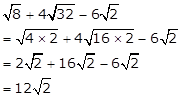
Thus, the given number is irrational.
Solution 7
(i) Number of chocolates distributed by Reema
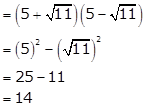
(ii) Loving, helping and caring attitude towards poor and needy children.
Solution 8(i)
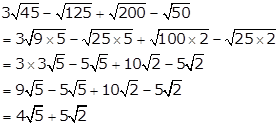
Solution 8(ii)
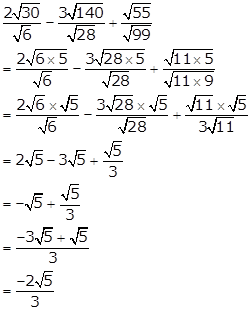
Solution 8(iii)
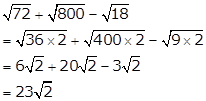
Number Systems Exercise Ex. 1G
Solution 1(iii)

Solution 1(i)
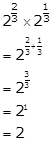
Solution 1(ii)
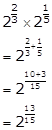
Solution 1(iv)
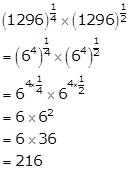
Solution 2(i)
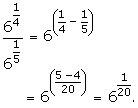
Solution 2(ii)
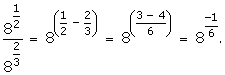
Solution 2(iii)
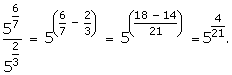
Solution 3(i)
![]()
Solution 3(ii)
![]()
Solution 3(iii)
![]()
Solution 4(i)
![]()
Solution 4(ii)
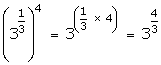
Solution 4(iii)
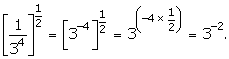
Solution 5(i)
![]()
Solution 5(ii)
![]()
Solution 5(iii)

Solution 5(iv)
![]()
Solution 5(v)

Solution 5(vi)

Solution 6(i)
Given, a = 2 and b = 3
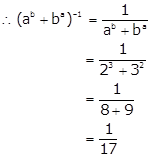
Solution 6(ii)
Given, a = 2 and b = 3

Solution 7(i)
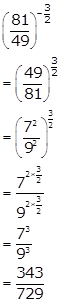
Solution 7(ii)
(14641)0.25
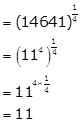
Solution 7(iii)
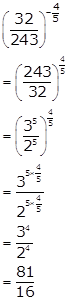
Solution 7(iv)
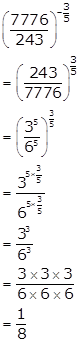
Solution 8(i)
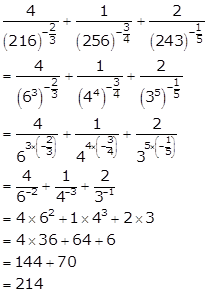
Solution 8(ii)

Solution 8(iii)
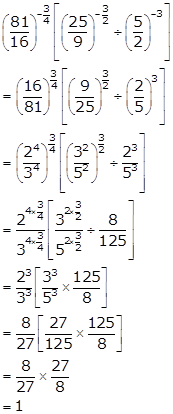
Solution 8(iv)
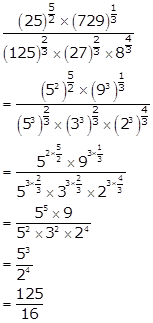
Solution 9(i)
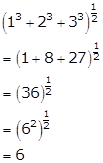
Solution 9(ii)
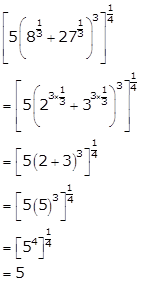
Solution 9(iii)
![]()
Solution 9(iv)
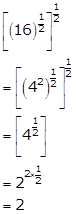
Solution 10(i)
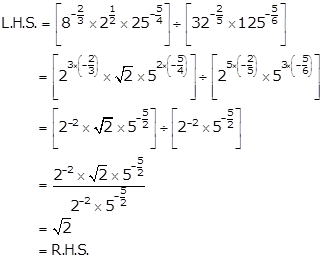
Solution 10(ii)

Solution 10(iii)
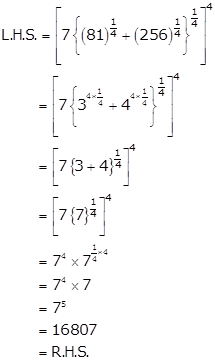
Solution 11
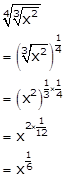
Solution 12
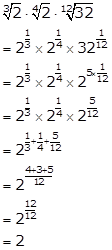
Solution 13(i)
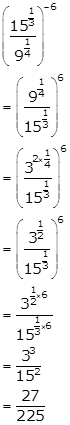
Solution 13(ii)

Solution 13(iii)
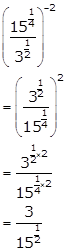
Solution 14(i)
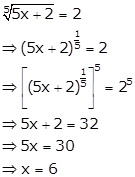
Solution 14(ii)
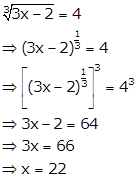
Solution 14(iii)
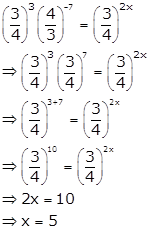
Solution 14(iv)
5x - 3 × 32x - 8 = 225
⇒ 5x - 3× 32x - 8 = 52 × 32
⇒ x - 3 = 2 and 2x - 8 = 2
⇒ x = 5 and 2x = 10
⇒ x = 5
Solution 14(v)
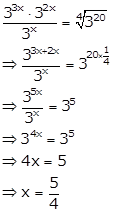
Solution 15(i)
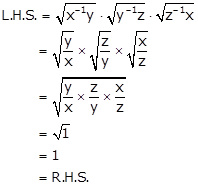
Solution 15(ii)
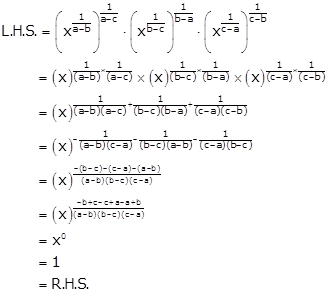
Solution 15(iii)

Solution 15(iv)
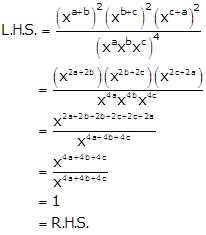
Solution 16
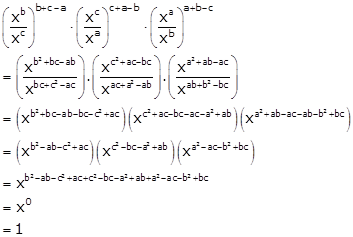
Solution 17
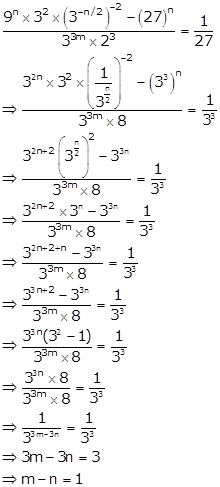
Solution 18
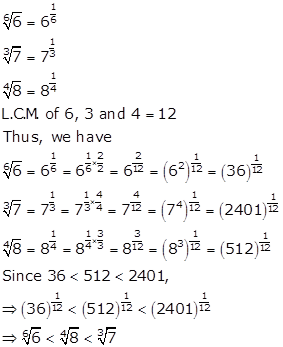
Number Systems Exercise Ex. 1A
Solution 1
A
number which can be expressed as ![]() , where 'a' and 'b' both are integers and b ≠ 0, is called
a rational number.
, where 'a' and 'b' both are integers and b ≠ 0, is called
a rational number.
Since,
0 can be expressed as ![]() , it is a rational number.
, it is a rational number.
Solution 2(i)
(i)![]()
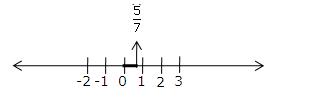
Solution 2(ii)
(ii)![]()
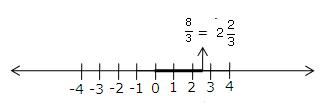
Solution 2(iii)
![]()
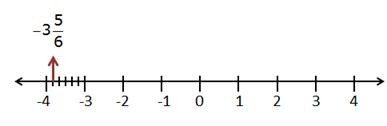
Solution 2(iv)
(iv) 1.3

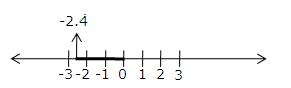
Solution 2(v)
(v) -2.4
Solution 3(i)
Solution 3(ii)
Solution 3(iii)
Solution 3(iv)
Solution 3(v)

Solution 4
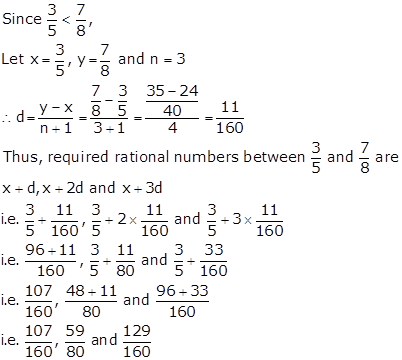
Infinite rational numbers can be determined between given two rational numbers.
Solution 5
We have
![]()
We know that 9 < 10 < 11 < 12 < 13 < 14 < 15
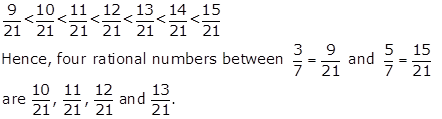
Solution 6
2 and 3 can be
represented as![]() respectively.
respectively.
Now six rational numbers between 2 and 3 are
![]() .
.
Solution 7
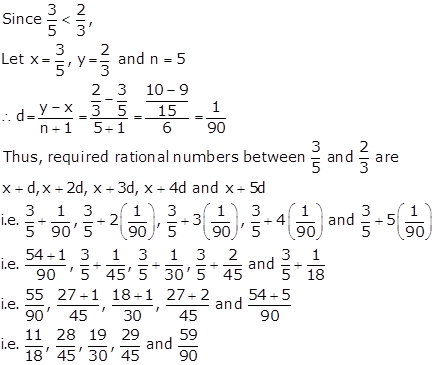
Solution 8
Let x = 2.1 and y = 2.2
Then, x < y because 2.1 < 2.2
Or we can say that, ![]()
Or, ![]()
That is, we have, ![]()
We know that,
![]()
Therefore, we can have,
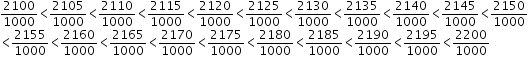
Therefore, 16 rational numbers between, 2.1 and 2.2 are:

So, 16 rational numbers between 2.1 and 2.2 are:
2.105, 2.11, 2.115, 2.12, 2.125, 2.13, 2.135, 2.14, 2.145, 2.15, 2.155, 2.16, 2.165, 2.17, 2.175, 2.18
Solution 9(i)
True. Since the collection of natural number is a sub collection of whole numbers, and every element of natural numbers is an element of whole numbers
Solution 9(ii)
False. Since 0 is whole number but it is not a natural number.
Solution 9(iii)
False, integers include negative of natural numbers as well, which are clearly not whole numbers. For example -1 is an integer but not a whole number.
Solution 9(iv)
True. Every integer can be represented in a fraction form with denominator 1.
Solution 9(v)
False,
integers are counting numbers on both sides of the number line i.e. they are
both positive and negative while rational numbers are of the form ![]() . Hence, Every rational number is not an integer but every
integer is a rational number.
. Hence, Every rational number is not an integer but every
integer is a rational number.
Solution 9(vi)
False. Since division of whole numbers is not closed under division, the value of ![]() , may not be a whole number.
, may not be a whole number.
Number Systems Exercise Ex. 1E
Solution 1
Draw a number line as shown.
On the number line, take point O corresponding to zero.
Now take point A on number line such that OA = 2 units.
Draw perpendicular AZ at A on the number line and cut-off arc AB = 1 unit.
By Pythagoras Theorem,
OB2 = OA2 + AB2 = 22 + 12 = 4 + 1 = 5
⇒ OB = ![]()
Taking O as centre and OB = ![]() as radius draw an
arc cutting real line at C.
as radius draw an
arc cutting real line at C.
Clearly, OC = OB = ![]()

Hence, C represents ![]() on the number line.
on the number line.
Solution 2
Draw a number line as shown.
On the number line, take point O corresponding to zero.
Now take point A on number line such that OA = 1 unit.
Draw perpendicular AZ at A on the number line and cut-off arc AB = 1 unit.
By Pythagoras Theorem,
OB2 = OA2 + AB2 = 12 + 12 = 1 + 1 = 2
⇒ OB = ![]()
Taking O as centre and OB = ![]() as radius draw an
arc cutting real line at C.
as radius draw an
arc cutting real line at C.
Clearly, OC = OB = ![]()
Thus, C represents ![]() on the number line.
on the number line.
Now, draw perpendicular CY at C on the number line and cut-off arc CE = 1 unit.
By Pythagoras Theorem,
OE2 = OC2
+ CE2 = ![]() 2 + 12 = 2 + 1 = 3
2 + 12 = 2 + 1 = 3
⇒ OE = ![]()
Taking O as centre and OE = ![]() as radius draw an
arc cutting real line at D.
as radius draw an
arc cutting real line at D.
Clearly, OD = OE = ![]()
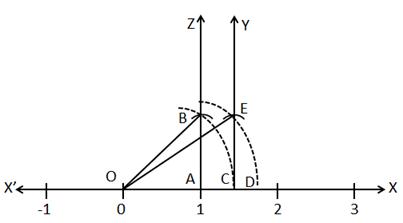
Hence, D represents ![]() on the number line.
on the number line.
Solution 3
Draw a number line as shown.
On the number line, take point O corresponding to zero.
Now take point A on number line such that OA = 3 units.
Draw perpendicular AZ at A on the number line and cut-off arc AB = 1 unit.
By Pythagoras Theorem,
OB2 = OA2 + AB2 = 32 + 12 = 9 + 1 = 10
⇒ OB = ![]()
Taking O as centre and OB = ![]() as radius draw an
arc cutting real line at C.
as radius draw an
arc cutting real line at C.
Clearly, OC = OB = ![]()

Hence,
C represents ![]() on the number line.
on the number line.
Solution 4
Draw a number line as shown.
On the number line, take point O corresponding to zero.
Now take point A on number line such that OA = 2 units.
Draw perpendicular AZ at A on the number line and cut-off arc AB = 2 units.
By Pythagoras Theorem,
OB2 = OA2 + AB2 = 22 + 22 = 4 + 4 = 8
⇒ OB = ![]()
Taking O as centre and OB = ![]() as radius draw an
arc cutting real line at C.
as radius draw an
arc cutting real line at C.
Clearly, OC = OB = ![]()

Hence,
C represents ![]() on the number line.
on the number line.
Solution 5
Draw a line segment AB = 4.7 units and extend it to C such that BC = 1 unit.
Find the midpoint O of AC.
With O as centre and OA as radius, draw a semicircle.
Now, draw BD ⊥ AC, intersecting the semicircle at D.
Then,
BD = ![]() units.
units.
With B as centre and BD as radius, draw an arc, meeting AC produced at E.
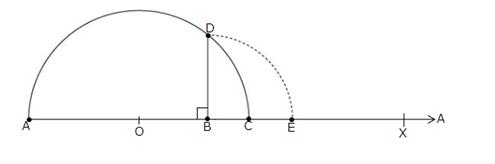 Then, BE = BD =
Then, BE = BD = ![]() units.
units.
Solution 6
Draw a line segment OB = 10.5 units and extend it to C such that BC = 1 unit.
Find the midpoint D of OC.
With D as centre and DO as radius, draw a semicircle.
Now, draw BE ⊥ AC, intersecting the semicircle at E.
Then,
BE = ![]() units.
units.
With B as centre and BE as radius, draw an arc, meeting AC produced at F.
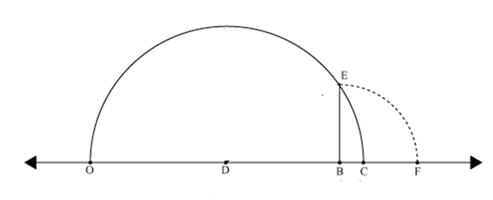
Then, BF = BE = ![]() units.
units.
Solution 7
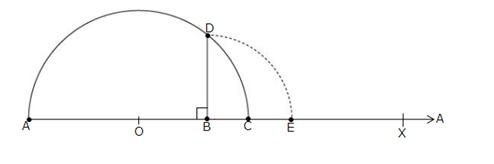
Draw a line segment AB = 7.28 units and extend it to C such that BC = 1 unit.
Find the midpoint O of AC.
With O as centre and OA as radius, draw a semicircle.
Now, draw BD ![]() AC, intersecting the semicircle at D.
AC, intersecting the semicircle at D.
Then, BD = ![]() units.
units.
With D as centre and BD as radius, draw an arc, meeting AC produced at E.
Then, BE = BD = ![]() units.
units.
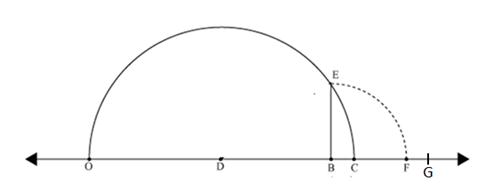
Solution 8
Draw a line segment OB = 9.5 units and extend it to C such that BC = 1 unit.
Find the midpoint D of OC.
With D as centre and DO as radius, draw a semicircle.
Now, draw BE ⊥ AC, intersecting the semicircle at E.
Then,
BE = ![]() units.
units.
With B as centre and BE as radius, draw an arc, meeting AC produced at F.
Then,
BF = BE = ![]() units.
units.
Extend BF to G such that FG = 1 unit.
Then,
BG = ![]()
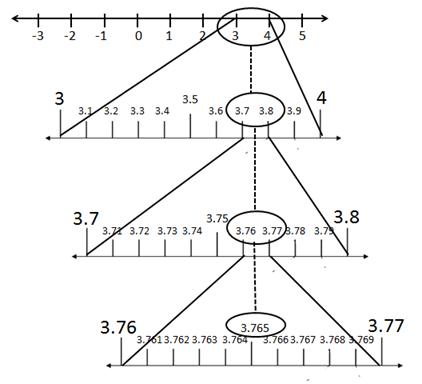
Solution 9
Solution 10
![]()

Number Systems Exercise Ex. 1F
Solution 1
The rationalising factor of the denominator in ![]() is
is ![]()
Solution 2(i)
On multiplying the numerator and denominator of the given number by ![]() , we get
, we get
Solution 2(ii)
On multiplying the numerator and denominator of the given number by ![]() , we get
, we get
Solution 2(iii)
Solution 2(iv)
Solution 2(v)
Solution 2(vi)
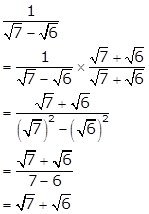
Solution 2(vii)
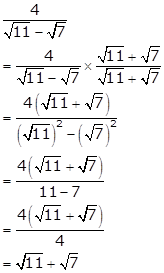
Solution 2(viii)

Solution 2(ix)
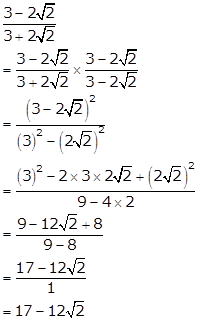
Solution 3(i)
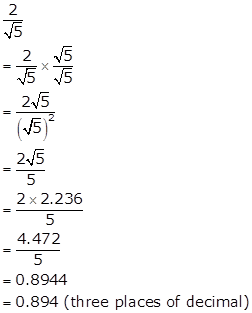
Solution 3(ii)
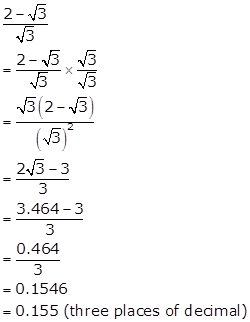
Solution 3(iii)
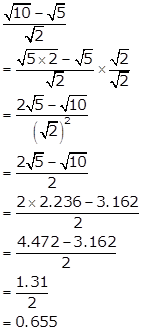
Solution 4(i)
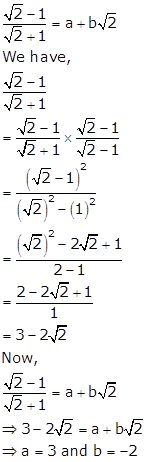
Solution 4(ii)
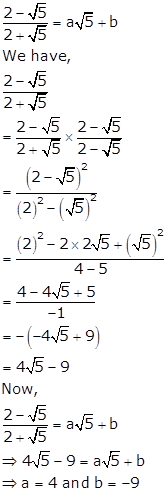
Solution 4(iii)
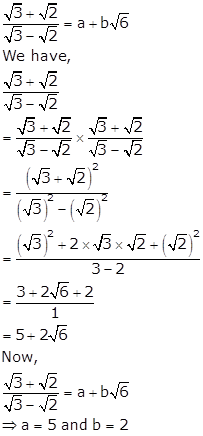
Solution 4(iv)
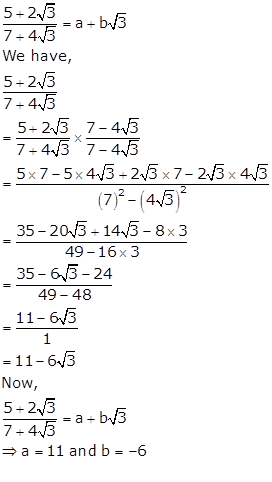
Solution 5(i)
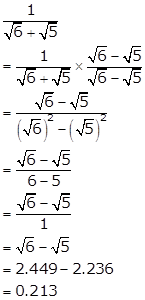
Solution 5(ii)
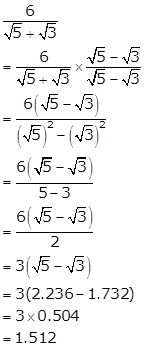
Solution 5(iii)
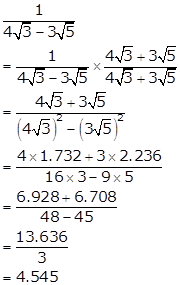
Solution 5(iv)
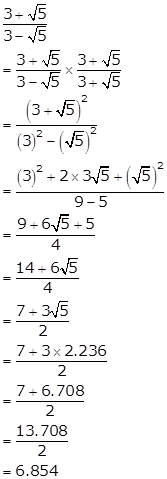
Solution 5(v)
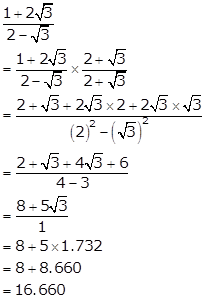
Solution 5(vi)
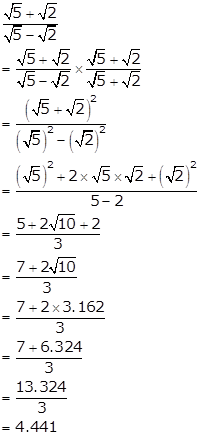
Solution 6(i)
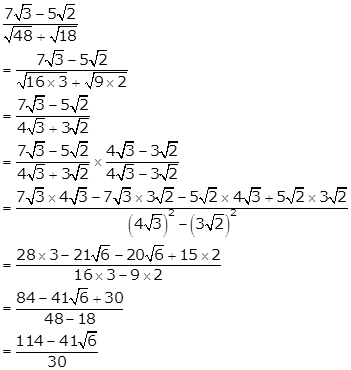
Solution 6(ii)

Solution 7(i)
Solution 7(ii)
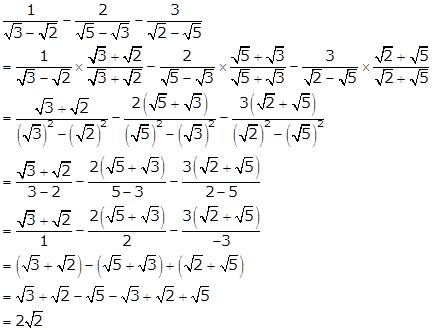
Solution 7(iii)
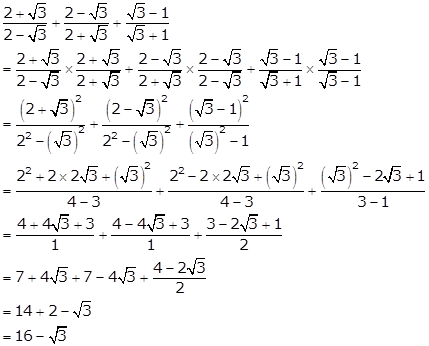
Solution 7(iv)
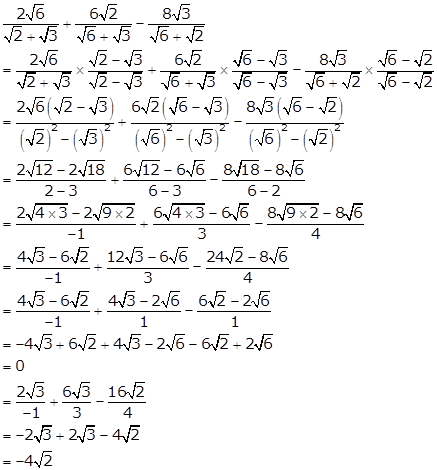
Solution 8(i)
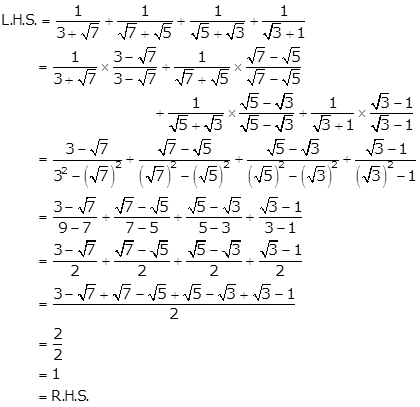
Solution 8(ii)

Solution 9
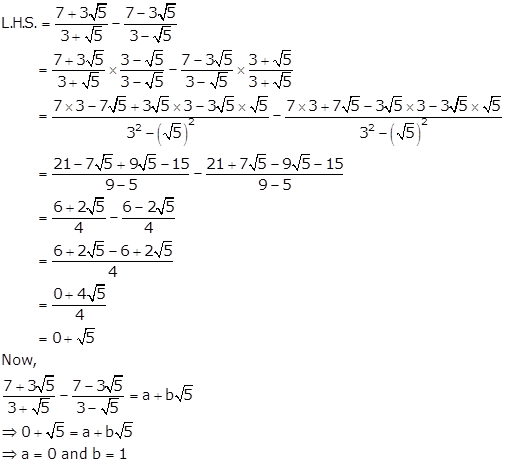 *Back answer incorrect
*Back answer incorrect
Solution 10
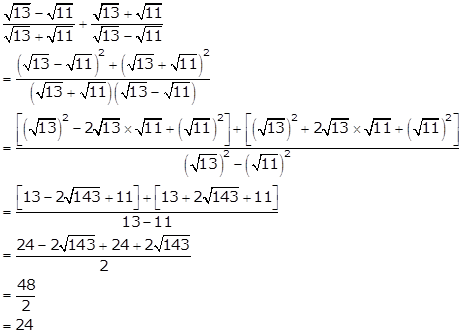
Solution 11

Thus, the given number is rational.
Solution 12

Solution 13

Solution 14
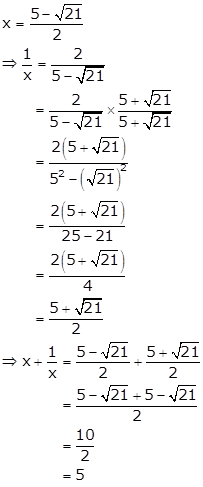
Solution 15
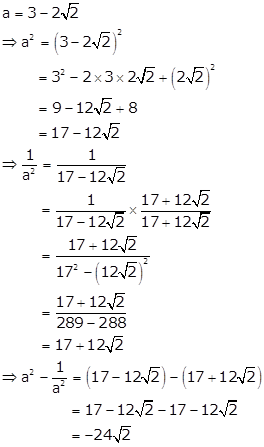
Solution 16
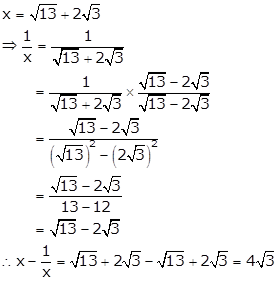
Solution 17
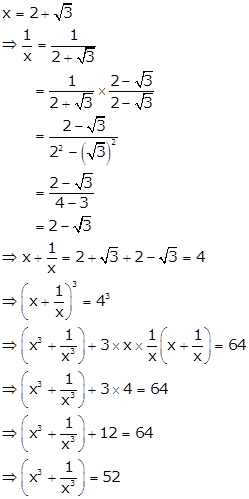
Solution 18

Solution 19

Solution 20
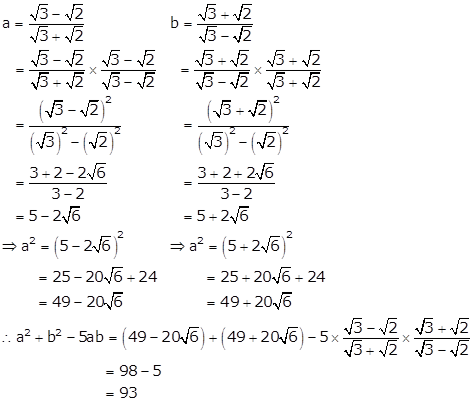
Solution 21

Solution 22(i)
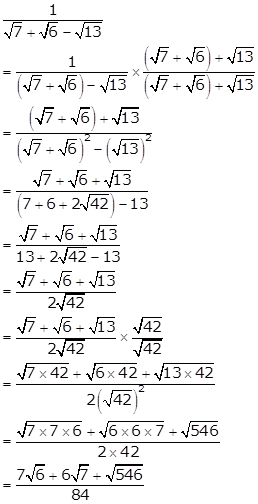
Solution 22(ii)
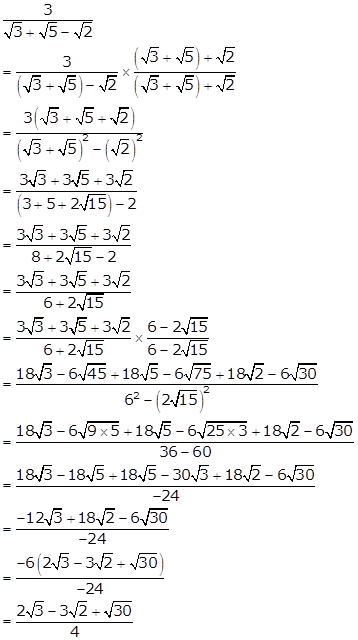
Solution 22(iii)
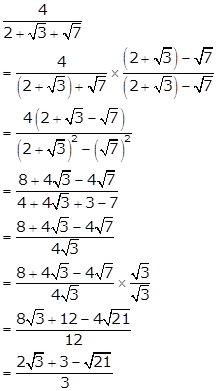
Solution 23
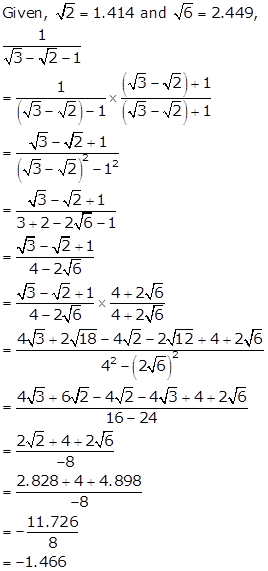
Solution 24
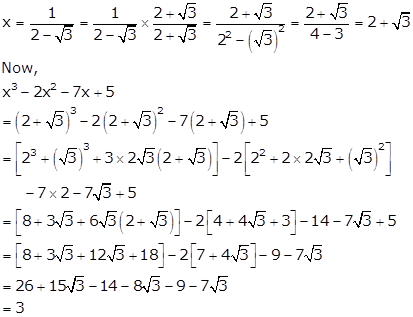
Solution 25