Class 9 R S AGGARWAL AND V AGGARWAL Solutions Maths Chapter 4 - Linear Equations in Two Variables
Linear Equations in Two Variables Exercise MCQ
Solution 1
Correct option: (b)
The equation of the x-axis is y = 0.
Solution 2
Correct option: (a)
The equation of the y-axis is x = 0.
Solution 3

Solution 4

Solution 5

Solution 6
Correct option: (a)
The equation 2x + 5y = 7 has a unique solution, if x and y are natural numbers.
If we take x = 1 and y = 1, the given equation is satisfied.
Solution 7
Correct option: (c)
The graph of y = 5 is a line parallel to the x-axis at a distance of 5 units from the origin.
Solution 8
Correct option: (d)
The graph of x = 4 is a line parallel to the y-axis at a distance of 4 units from the origin.
Solution 9
Correct option: (c)
The graph of x + 3 = 0 is a line parallel to the y-axis at a distance of 3 units to the left of y-axis.
Solution 10
Correct option: (c)
The graph of y + 2 = 0 is a line parallel to the x-axis at a distance of 2 units below the x-axis.
Solution 11
Correct option: (c)
When a graph meets the y-axis, the x coordinate is zero.
Thus, substituting x = 0 in the given equation, we get
2(0) + 3y = 6
⇒ 3y = 6
⇒ y = 2
Hence, the required point is (0, 2).
Solution 12
Correct option: (c)
When a graph meets the x-axis, the y coordinate is zero.
Thus, substituting y = 0 in the given equation, we get
2x + 5(0) = 10
⇒ 2x = 10
⇒ x = 5
Hence, the required point is (5, 0).
Solution 13
![]()
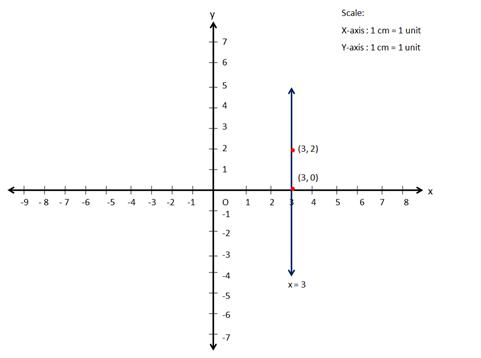
Solution 14
Correct option: (c)
Since, the y coordinate is 3, the graph of the line y = 3 passes through the point (2, 3).
Solution 15
![]()
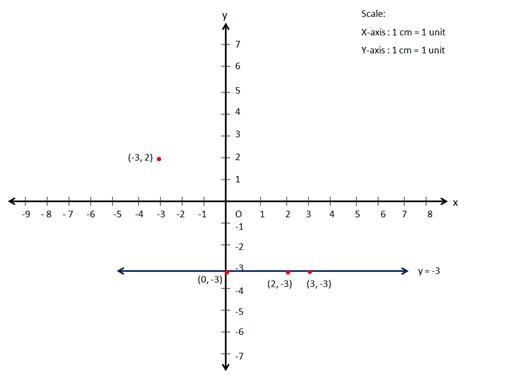
Solution 16

Solution 17

Solution 18
Correct option: (d)
Infinitely many linear equations can be satisfied by x = 2 and y = 3.
Solution 19

Solution 20
Correct option: (d)
Since, (2, 0) is a solution of the linear equation 2x + 3y = k, substituting x = 2 and y = 0 in the given equation, we have
2(2) + 3(0) = k
⇒ 4 + 0 = k
⇒ k = 4
Solution 21
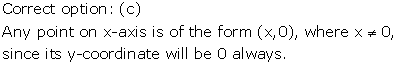
Solution 22

Solution 23
Correct option: (c)
Substituting x = 5 and y = 2 in L.H.S. of equation x + y = 7, we get
L.H.S. = 5 + 2 = 7 = R.H.S.
Hence, x = 5 and y = 2 is a solution of the linear equation x + y = 7.
Solution 24
Correct option: (b)
Since the point (3, 4) lies on the graph of 3y = ax + 7, substituting x = 3 and y = 4 in the given equation, we get
3(4) = a(3) + 7
⇒ 12 = 3a + 7
⇒ 3a = 5
![]()
Linear Equations in Two Variables Exercise Ex. 4B
Solution 1(vii)
y + 5 = 0
⇒ y = -5, which is a line parallel to the X-axis, at a distance of 5 units from it, below the X-axis.
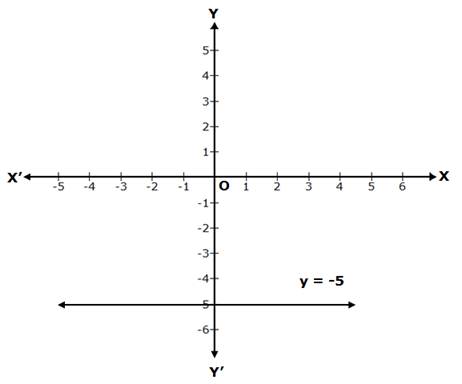
Solution 1(viii)
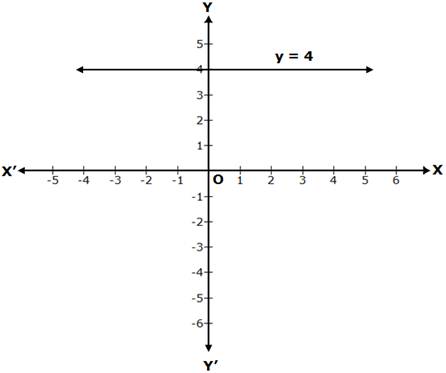
y = 4 is a line parallel to the X-axis, at a distance of 4 units from it, above the X-axis.
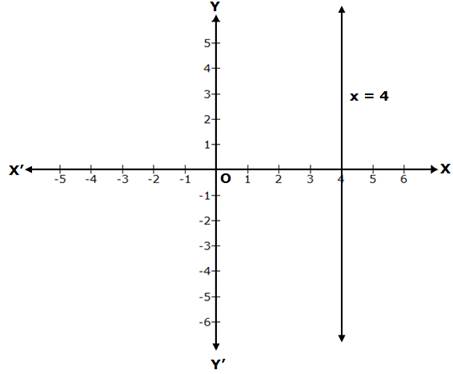
Solution 1(i)
x = 4 is a line parallel to the Y-axis, at a distance of 4 units from it, to its right.
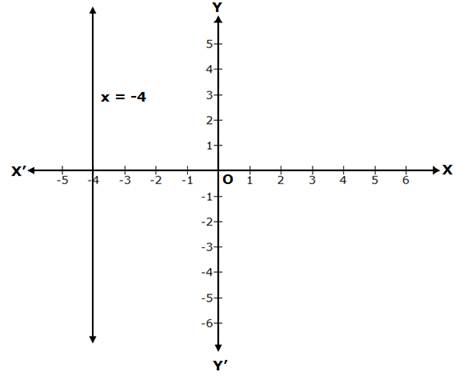
Solution 1(ii)
x + 4 = 0
⇒ x = -4, which is a line parallel to the Y-axis, at a distance of 4 units from it, to its left.
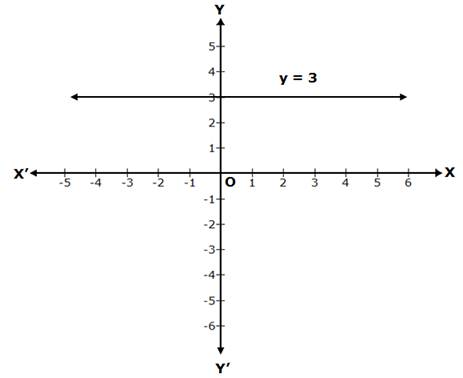
Solution 1(iii)
y = 3 is a line parallel to the X-axis, at a distance of 3 units from it, above the X-axis.
Solution 1(iv)
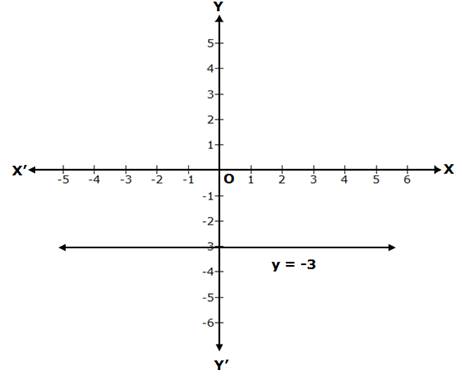
y = -3 is a line parallel to the X-axis, at a distance of 3 units from it, below the X-axis.
Solution 1(v)
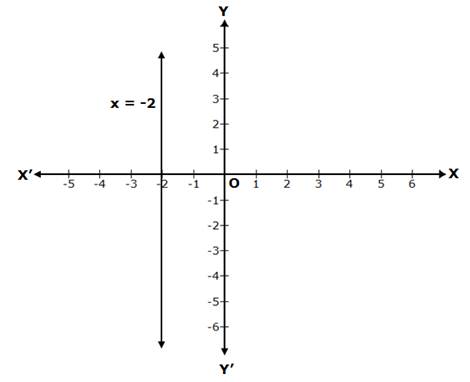
x = -2 is a line parallel to the Y-axis, at a distance of 2 units from it, to its left.
Solution 1(vi)
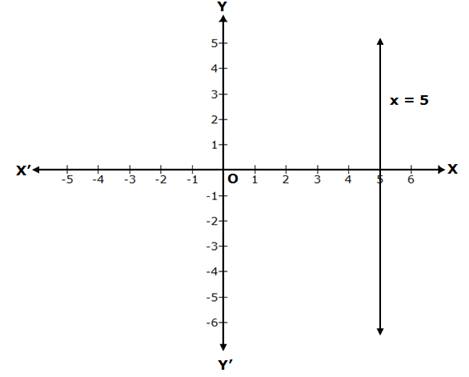
x = 5 is a line parallel to the Y-axis, at a distance of 5 units from it, to its right.
Solution 2(i)
y = 3x
When x = 1, then y = 3(1) = 3
When x = -1, then y = 3(-1) = -3
Thus, we have the following table:
|
x |
1 |
-1 |
|
y |
3 |
-3 |
Now, plot the points A(1, 3) and B(-1, -3) on a graph paper.
Join AB and extend it in both the directions.
Then, the line AB is the required graph of y = 3x.
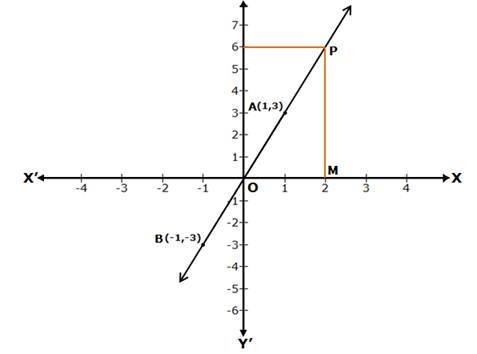
Reading the graph
Given: x = 2. Take a point M on the X-axis such that OM = 2.
Draw MP parallel to the Y-axis, cutting the line AB at P.
Clearly, PM = 6
Thus, when x = 2, then y = 6.
Solution 2(ii)
The given equation is y = 3x.
Putting
x = 1, y = 3 ![]() 1 = 3
1 = 3
Putting
x = 2, y = 3 ![]() 2 = 6
2 = 6
Thus, we have the following table:
|
x |
1 |
2 |
|
y |
3 |
6 |
Plot points (1,3) and (2,6) on a graph paper and join them to get the required graph.
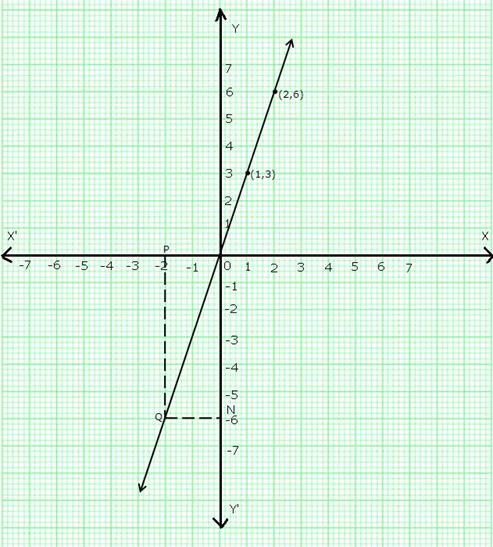
Take a point P on the left of y-axis such that the distance of point P from the y-axis is 2 units.
Draw PQ parallel to y-axis cutting the line y = 3x at Q. Draw QN parallel to x-axis meeting y-axis at N.
So, y = ON = -6.
Solution 3(ii)
x + 2y - 3 = 0
⇒ 2y = 3 - x
![]()
When
x = -1, then ![]()
When
x = 1, then ![]()
Thus, we have the following table:
|
x |
-1 |
1 |
|
y |
2 |
1 |
Now, plot the points A(-1, 2) and B(1, 1) on a graph paper.
Join AB and extend it in both the directions.
Then, the line AB is the required graph of x + 2y - 3 = 0.
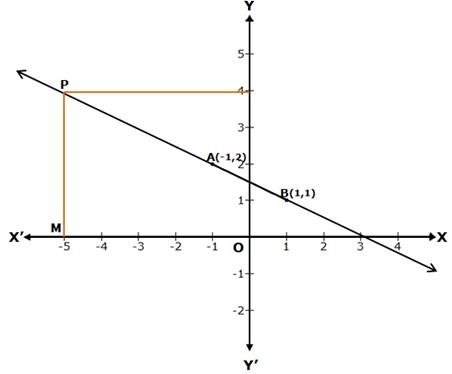
Reading the graph
Given: x = -5. Take a point M on the X-axis such that OM = -5.
Draw MP parallel to the Y-axis, cutting the line AB at P.
Clearly, PM = 4
Thus, when x = -5, then y = 4.
Solution 3(i)
The given equation is,
x + 2y - 3 = 0
![]() x = 3 - 2y
x = 3 - 2y
Putting y = 1,x = 3 - (2 ![]() 1) = 1
1) = 1
Putting y = 0,x = 3 - (2 ![]() 0) = 3
0) = 3
Thus, we have the following table:
|
x |
1 |
3 |
|
y |
1 |
0 |
Plot points (1,1) and (3,0) on a graph paper and join them to get the required graph.
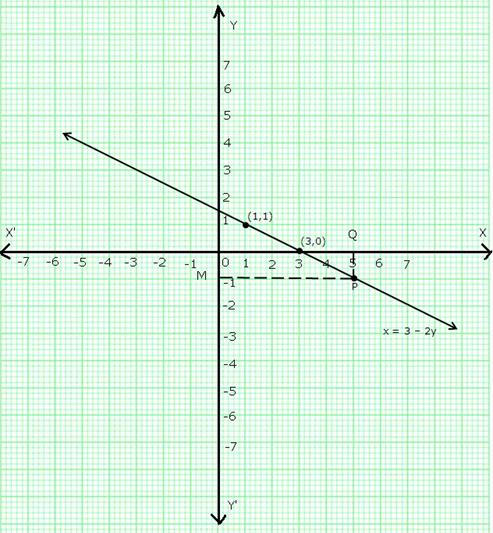
Take a point Q on x-axis such that OQ = 5.
Draw QP parallel to y-axis meeting the line (x = 3 - 2y) at P.
Through P, draw PM parallel to x-axis cutting y-axis at M.
So, y = OM = -1.
Solution 4
The given equation is, 2x - 3y = 5
![]()
Now, if x = 4, then
![]()
And, if x = -2, then
![]()
Thus, we have the following table:
|
x |
4 |
-2 |
|
y |
1 |
-3 |
Plot points (4,1) and (-2,-3) on a graph paper and join them to get the required graph.
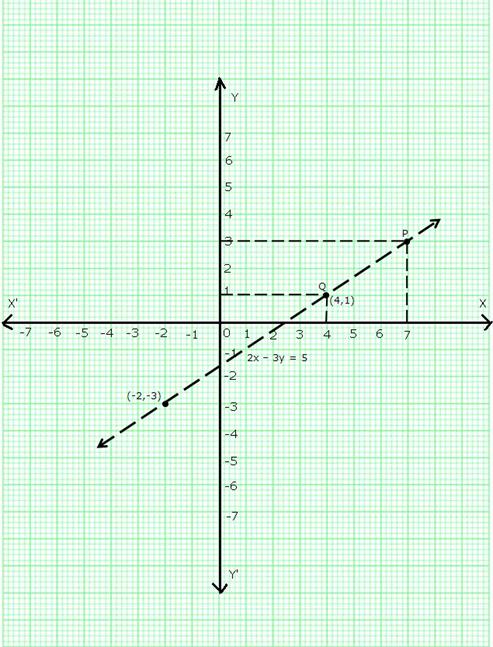
(i) When x = 4, draw a line parallel to y-axis at a distance of 4 units from y-axis to its right cutting the line at Q and through Q draw a line parallel to x-axis cutting y-axis which is found to be at a distance of 1 units above x-axis.
Thus, y = 1 when x = 4.
(ii) When y = 3, draw a line parallel to x-axis at a distance of 3 units from x-axis and above it, cutting the line at point P. Through P, draw a line parallel to y-axis meeting x-axis at a point which is found be 7 units to the right of y axis.
Thus, when y = 3, x = 7.
Solution 5
The given equation is 2x + y = 6
![]() y = 6 - 2x
y = 6 - 2x
Now, if x = 1, then y = 6 - 2 ![]() 1 = 4
1 = 4
And, if x = 2, then y = 6 - 2 ![]() 2 = 2
2 = 2
Thus, we have the following table:
|
x |
1 |
2 |
|
y |
4 |
2 |
Plot points (1,4) and (2,2) on a graph paper and join them to get the required graph.
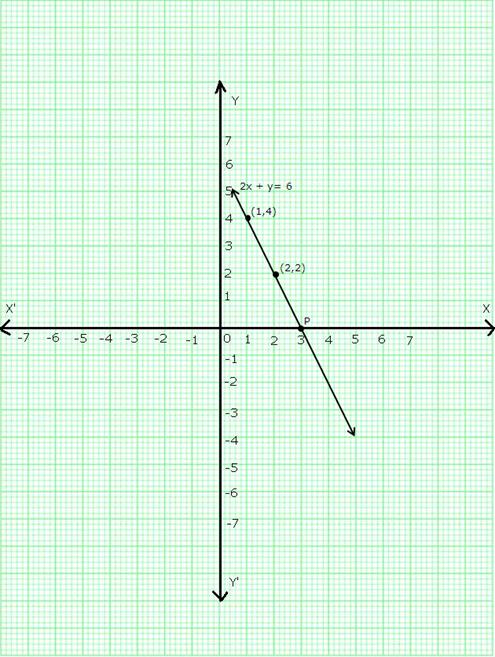
We find that the line cuts the x-axis at a point P which is at a distance of 3 units to the right of y-axis.
So, the co-ordinates of P are (3,0).
Solution 6
The given equation is 3x + 2y = 6
![]() 2y = 6 - 3x
2y = 6 - 3x
![]()
![]()
Now, if x = 2, then
![]()
And, if x = 4, then
![]()
Thus, we have the following table:
|
x |
2 |
4 |
|
y |
0 |
-3 |
Plot points (2, 0) and (4,-3) on a graph paper and join them to get the required graph.
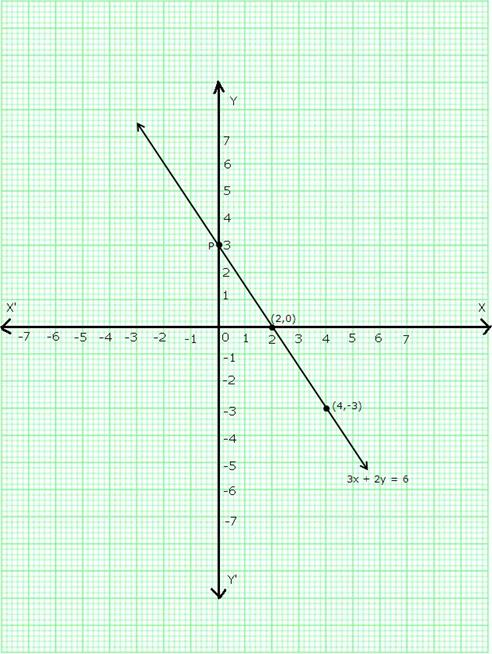
We find that the line 3x + 2y = 6 cuts the y-axis at a point P which is 3 units above the x-axis.
So, co-ordinates of P are (0,3).
Solution 7
Graph of the equation 3x - 2y = 4
⇒ 2y = 3x - 4
![]()
When
x = 2, then ![]()
When
x = -2, then ![]()
Thus, we have the following table:
|
x |
2 |
-2 |
|
y |
1 |
-5 |
Now, plot the points A(2, 1) and B(-2, -5) on a graph paper.
Join AB and extend it in both the directions.
Then, the line AB is the required graph of 3x - 2y = 4.
Graph of the equation x + y - 3 = 0
⇒ y = 3 - x
When x = 1, then y = 3 - 1 = 2
When x = -1, then y = 3 - (-1) = 4
Thus, we have the following table:
|
x |
1 |
-1 |
|
y |
2 |
4 |
Now, plot the points C(1, 2) and D(-1, 4) on a graph paper.
Join CD and extend it in both the directions.
Then, the line CD is the required graph of x + y - 3 = 0.
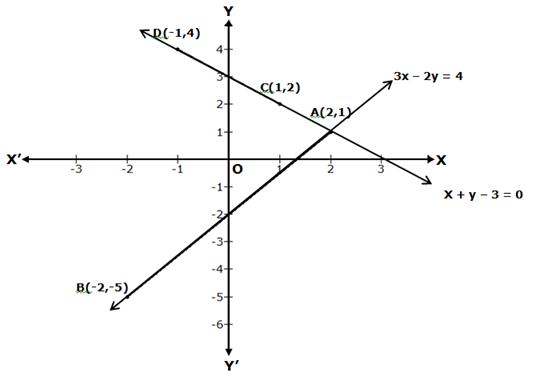
The two graph lines intersect at point A(2, 1).
Solution 8(i)
4x + 3y = 24
⇒ 3y = 24 - 4x
![]()
When
x = 0, then ![]()
When
x = 3, then ![]()
Thus, we have the following table:
|
x |
0 |
3 |
|
y |
8 |
4 |
Now, plot the points A(0, 8) and B(3, 4) on a graph paper.
Join AB and extend it in both the directions.
Then, the line AB is the required graph of 4x + 3y = 24.
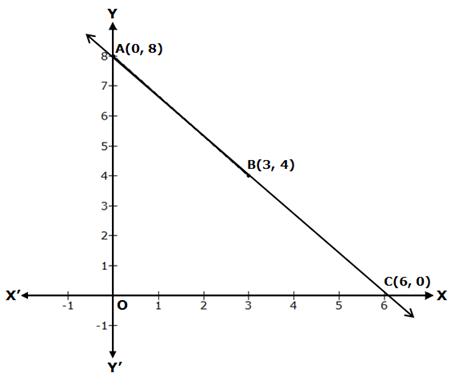
Reading the graph
The graph of line 4x + 3y = 24 intersects the X-axis at point C(6, 0) and the Y-axis at point A(0, 8).
Solution 8(ii)
4x + 3y = 24
⇒ 3y = 24 - 4x
![]()
When
x = 0, then ![]()
When
x = 3, then ![]()
Thus, we have the following table:
|
x |
0 |
3 |
|
y |
8 |
4 |
Now, plot the points A(0, 8) and B(3, 4) on a graph paper.
Join AB and extend it in both the directions.
Then, the line AB is the required graph of 4x + 3y = 24.

Reading the graph
Required area = Area of ΔAOC
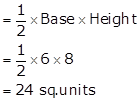
Solution 9
Graph of the equation 2x + y = 6
⇒ y = 6 - 2x
When x = 1, then y = 6 - 2(1) = 6 - 2 = 4
When x = 2, then y = 6 - 2(2) = 6 - 4 = 2
Thus, we have the following table:
|
x |
1 |
2 |
|
y |
4 |
2 |
Now, plot the points A(1, 4) and B(2, 2) on a graph paper.
Join AB and extend it in both the directions.
Then, the line AB is the required graph of 2x + y = 6.
Graph of the equation 2x - y + 2 = 0
⇒ y = 2x + 2
When x = -1, then y = 2(-1) + 2 = -2 + 2 = 0
When x = 2, then y = 2(2) + 2 = 4 + 2 = 6
Thus, we have the following table:
|
x |
-1 |
2 |
|
y |
0 |
6 |
Now, plot the points C(-1, 0) and D(2, 6) on a graph paper.
Join CD and extend it in both the directions.
Then, the line CD is the required graph of 2x - y + 2 = 0.
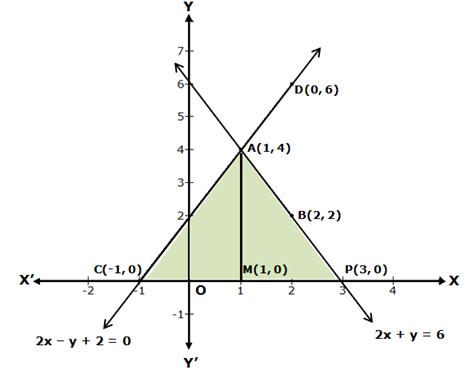
The two graph lines intersect at point A(1, 4).
The area enclosed by the lines and X-axis is shown in the graph.
Draw AM perpendicular from A on X-axis.
PM = y-coordinate of point A(1, 4) = 4
And, CP = 4
Area of shaded region = Area of ΔACP
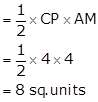
Solution 10
Graph of the equation x - y = 1
⇒ y = x - 1
When x = 1, then y = 1 - 1 = 0
When x = 2, then y = 2 - 1 = 1
Thus, we have the following table:
|
x |
1 |
2 |
|
y |
0 |
1 |
Now, plot the points A(1, 0) and B(2, 1) on a graph paper.
Join AB and extend it in both the directions.
Then, the line AB is the required graph of x - y = 1.
Graph of the equation 2x + y = 8
⇒ y = 8 - 2x
When x = 2, then y = 8 - 2(2) = 8 - 4 = 4
When x = 3, then y = 8 - 2(3) = 8 - 6 = 2
Thus, we have the following table:
|
x |
2 |
3 |
|
y |
4 |
2 |
Now, plot the points C(2, 4) and D(3, 2) on a graph paper.
Join CD and extend it in both the directions.
Then, the line CD is the required graph of 2x + y = 8.
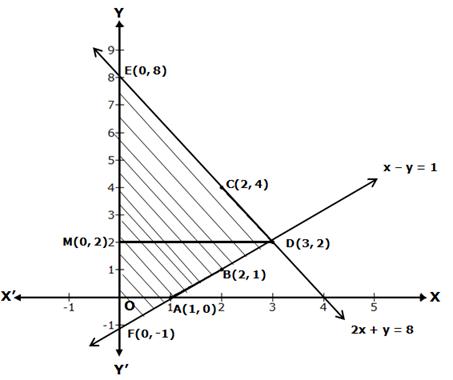
The two graph lines intersect at point D(3, 2).
The area enclosed by the lines and Y-axis is shown in the graph.
Draw DM perpendicular from D on Y-axis.
DM = x-coordinate of point D(3, 2) = 3
And, EF = 9
Area of shaded region = Area of ΔDEF
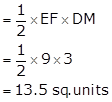
Solution 11
Graph of the equation x + y = 6
⇒ y = 6 - x
When x = 2, then y = 6 - 2 = 4
When x = 3, then y = 6 - 3 = 3
Thus, we have the following table:
|
x |
2 |
3 |
|
y |
4 |
3 |
Now, plot the points A(2, 4) and B(3, 3) on a graph paper.
Join AB and extend it in both the directions.
Then, the line AB is the required graph of x + y = 6.
Graph of the equation x - y = 2
⇒ y = x - 2
When x = 3, then y = 3 - 2 = 1
When x = 4, then y = 4 - 2 = 2
Thus, we have the following table:
|
x |
3 |
4 |
|
y |
1 |
2 |
Now, plot the points C(3, 1) and D(4, 2) on a graph paper.
Join CD and extend it in both the directions.
Then, the line CD is the required graph of x - y = 2.
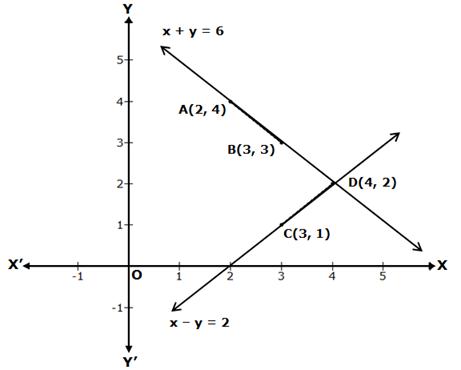
The two graph lines intersect at point D(4, 2).
Solution 12
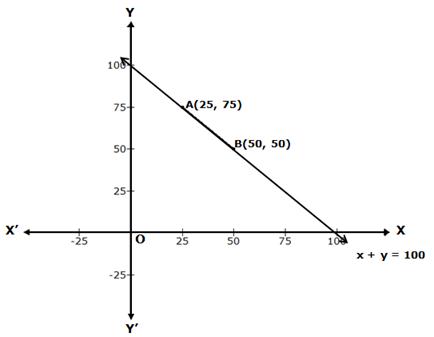
Let the amount contributed by students A and B be Rs. x and Rs. y respectively.
Total contribution = 100
⇒ x + y = 100
⇒ y = 100 - x
When x = 25, then y = 100 - 25 = 75
When x = 50, then y = 100 - 50 = 50
Thus, we have the following table:
|
x |
25 |
50 |
|
y |
75 |
50 |
Now, plot the points A(25, 75) and B(50, 50) on a graph paper.
Join AB and extend it in both the directions.
Then, the line AB is the required graph of x + y = 100.
Linear Equations in Two Variables Exercise Ex. 4A
Solution 1(i)
We have,
3x + 5y = 7.5
⇒ 3x + 5y - 7.5 = 0
![]()
⇒ 6x + 10y - 15 = 0
On comparing this equation with ax + by + c = 0, we obtain
a = 6, b = 10 and c = -15
Solution 1(ii)
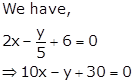
On comparing this equation with ax + by + c = 0, we obtain
a = 10, b = -1 and c = 30
Solution 1(iii)
We have,
3y - 2x = 6
⇒ -2x + 3y - 6 = 0
On comparing this equation with ax + by + c = 0, we obtain
a = -2, b = 3 and c = -6
Solution 1(iv)
We have,
4x = 5y
⇒ 4x - 5y = 0
On comparing this equation with ax + by + c = 0, we obtain
a = 4, b = -5 and c = 0
Solution 1(v)
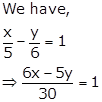
⇒ 6x - 5y = 30
⇒ 6x - 5y - 30 = 0
On comparing this equation with ax + by + c = 0, we obtain
a = 6, b = -5 and c = -30
Solution 1(vi)
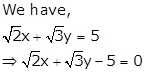
On comparing this equation with ax + by + c = 0, we obtain
a
= ![]() , b =
, b = ![]() and c = -5
and c = -5
Solution 2(i)
We have,
x = 6
⇒ x - 6 = 0
⇒ 1x + 0y - 6 = 0
⇒ x + 0y - 6 = 0
On comparing this equation with ax + by + c = 0, we obtain
a = 1, b = 0 and c = -6
Solution 2(ii)
We have,
3x - y = x - 1
⇒ 3x - x - y + 1 = 0
⇒ 2x - y + 1 = 0
On comparing this equation with ax + by + c = 0, we obtain
a = 2, b = -1 and c = 1
Solution 2(iii)
We have,
2x + 9 = 0
⇒ 2x + 0y + 9 = 0
On comparing this equation with ax + by + c = 0, we obtain
a = 2, b = 0 and c = 9
Solution 2(iv)
We have,
4y = 7
⇒ 0x + 4y - 7 = 0
On comparing this equation with ax + by + c = 0, we obtain
a = 0, b = 4 and c = -7
Solution 2(v)
We have,
x + y = 4
⇒ x + y - 4 = 0
On comparing this equation with ax + by + c = 0, we obtain
a = 1, b = 1 and c = -4
Solution 2(vi)
We have,
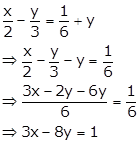
⇒ 3x - 8y - 1 = 0
On comparing this equation with ax + by + c = 0, we obtain
a = 3, b = -8 and c = -1
Solution 3(i)
Given equation is 5x - 4y = 20
Substituting x = 4 and y = 0 in L.H.S. of given equation, we get
L.H.S. = 5x - 4y
= 5(4) - 4(0)
= 20 - 0
= 20
= R.H.S.
Hence, (4, 0) is the solution of the given equation.
Solution 3(ii)
Given equation is 5x - 4y = 20
Substituting x = 0 and y = 5 in L.H.S. of given equation, we get
L.H.S. = 5x - 4y
= 5(0) - 4(5)
= 0 - 20
= -20
≠ R.H.S.
Hence, (0, 5) is not the solution of the given equation.
Solution 3(iii)
Given equation is 5x - 4y = 20
Substituting
x = -2 and y = ![]() in L.H.S. of given
equation, we get
in L.H.S. of given
equation, we get
L.H.S. = 5x - 4y
= 5(-2) - 4![]()
= -10 - 10
= -20
≠ R.H.S.
Hence,
![]() is not the
solution of the given equation.
is not the
solution of the given equation.
Solution 3(iv)
Given equation is 5x - 4y = 20
Substituting x = 0 and y = -5 in L.H.S. of given equation, we get
L.H.S. = 5x - 4y
= 5(0) - 4(-5)
= 0 + 20
= 20
= R.H.S.
Hence, (0, -5) is the solution of the given equation.
Solution 3(v)
Given equation is 5x - 4y = 20
Substituting
x = 2 and y = ![]() in L.H.S. of given
equation, we get
in L.H.S. of given
equation, we get
L.H.S. = 5x - 4y
= 5(2) - 4![]()
= 10 + 10
= 20
= R.H.S.
Hence,
![]() is the
solution of the given equation.
is the
solution of the given equation.
Solution 4(a)
Given equation is 2x - 3y = 6
Substituting x = 0 in the given equation, we get
2(0) - 3y = 6
⇒ 0 - 3y = 6
⇒ 3y = -6
⇒ y = -2
So, (0, -2) is the solution of the given equation.
Substituting y = 0 in the given equation, we get
2x - 3(0) = 6
⇒ 2x - 0 = 6
⇒ 2x = 6
⇒ x = 3
So, (3, 0) is the solution of the given equation.
Substituting x = 6 in the given equation, we get
2(6) - 3y = 6
⇒ 12 - 3y = 6
⇒ 3y = 6
⇒ y = 2
So, (6, 2) is the solution of the given equation.
Substituting y = 4 in the given equation, we get
2x - 3(4) = 6
⇒ 2x - 12 = 6
⇒ 2x = 18
⇒ x = 9
So, (9, 4) is the solution of the given equation.
Substituting x = -3 in the given equation, we get
2(-3) - 3y = 6
⇒ -6 - 3y = 6
⇒ 3y = -12
⇒ y = -4
So, (-3, -4) is the solution of the given equation.
Solution 4(b)
Given
equation is ![]()
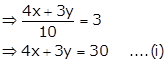
Substituting x = 0 in (i), we get
4(0) + 3y = 30
⇒ 3y = 30
⇒ y = 10
So, (0, 10) is the solution of the given equation.
Substituting x = 3 in (i), we get
4(3) + 3y = 30
⇒ 12 + 3y = 30
⇒ 3y = 18
⇒ y = 6
So, (3, 6) is the solution of the given equation.
Substituting x = -3 in (i), we get
4(-3) + 3y = 30
⇒ -12 + 3y = 30
⇒ 3y = 42
⇒ y = 14
So, (-3, 14) is the solution of the given equation.
Substituting y = 2 in (i), we get
4x + 3(2) = 30
⇒ 4x + 6 = 30
⇒ 4x = 24
⇒ x = 6
So, (6, 2) is the solution of the given equation.
Substituting y = -2 in (i), we get
4x + 3(-2) = 30
⇒ 4x - 6 = 30
⇒ 4x = 36
⇒ x = 9
So, (9, -2) is the solution of the given equation.
Solution 4(c)
Given equation is 3y = 4x
Substituting x = 3 in the given equation, we get
3y = 4(3)
⇒ 3y = 12
⇒ y = 4
So, (3, 4) is the solution of the given equation.
Substituting x = -3 in the given equation, we get
3y = 4(-3)
⇒ 3y = -12
⇒ y = -4
So, (-3, -4) is the solution of the given equation.
Substituting x = 9 in the given equation, we get
3y = 4(9)
⇒ 3y = 36
⇒ y = 12
So, (9, 12) is the solution of the given equation.
Substituting y = 8 in the given equation, we get
3(8) = 4x
⇒ 4x = 24
⇒ x = 6
So, (6, 8) is the solution of the given equation.
Substituting y = -8 in the given equation, we get
3(-8) = 4x
⇒ 4x = -24
⇒ x = -6
So, (-6, -8) is the solution of the given equation.
Solution 5
Since x = 3 and y = 4 is a solution of the equation 5x - 3y = k, substituting x = 3 and y = 4 in equation 5x - 3y = k, we get
5(3) - 3(4) = k
⇒ 15 - 12 = k
⇒ k = 3
Solution 6
Since x = 3k + 2 and y = 2k - 1 is a solution of the equation 4x - 3y + 1 = 0, substituting these values in equation, we get
4(3k + 2) - 3(2k - 1) + 1 = 0
⇒ 12k + 8 - 6k + 3 + 1 = 0
⇒ 6k + 12 = 0
⇒ 6k = -12
⇒ k = -2
Solution 7
Let the cost of one pencil be Rs. x and that of one ballpoint be Rs. y.
Then,
Cost of 5 pencils = Rs. 5x
Cost of 2 ballpoints = Rs. 2y
According to given statement, we have
5x = 2y
⇒ 5x - 2y = 0

