Class 9 R S AGGARWAL AND V AGGARWAL Solutions Maths Chapter 6: Introduction to Euclid's Geometry
Introduction to Euclid's Geometry Exercise MCQ
Solution 1
Correct option: (b)
Squares and circular altars were used for household rituals.
Whereas altars having shapes as combinations of rectangles, triangles and trapeziums were used for public worship.
Solution 2
Correct option: (b)
In ancient India, altars with combination of shapes like rectangles, triangles and trapeziums were used for public rituals.
Solution 3
Correct option: (c)
The Sriyantra consists of nine interwoven isosceles triangles.
Solution 4
Correct option: (b)
In Indus Valley Civilization (about 300 BC) the bricks used for construction work were having dimensions in the ratio is 4:2:1.
Solution 5
Correct option: (a)
The famous treatise 'The Elements' was divided into 13 chapters by Euclid.
Solution 6
Correct option: (b)
Euclid belongs to the country, Greece.
Solution 7
Correct option: (c)
Thales belongs to the country, Greece.
Solution 8
Correct option: (b)
Pythagoras was a student of Thales.
Solution 9
Correct option: (d)
A statement that requires a proof is called a theorem.
Solution 10
Correct option: (a)
'Lines are parallel if they do not intersect' is started in the form of a definition.
Solution 11
Correct option: (c)
Euclid stated that 'All right angles are equal to each other' in the form of a postulate.
This is Euclid's Postulate 4.
Note: The answer in the book is option (a). But if you have a look at the Euclid's postulate, the answer is a postulate.
Solution 12
Correct option: (d)
A pyramid is a solid figure, whose base is any polygon.
Solution 13
Correct option: (a)
The side faces of a pyramid are triangles.
Solution 14
Correct option: (c)
A solid has 3 dimensions.
Solution 15
Correct option: (b)
A surface has 2 dimensions.
Solution 16
Correct option: (a)
A point is an exact location. A fine dot represents a point. So, a point has 0 dimensions.
Solution 17
Correct option: (c)
Boundaries of solids are surfaces.
Solution 18
Correct option: (b)
Boundaries of surfaces are curves.
Solution 19
Correct option: (d)
The number of planes passing through three non-collinear points is 1.
Solution 20
Correct option: (d)
Axioms are assumed as universal truths in all branches of mathematics because they are taken for granted, without proof.
Solution 21
Correct option: (c)
Two lines are said to be parallel, if they have no point in common.
Options (a), (b) and (d) have a common point, hence they are not parallel.
In option (c), the floor and the ceiling of a room are parallel to each other is a true statement.
Solution 22
Correct option: (c)
In option (a), infinite number of line can be drawn to pass through a given point. So, it is not a true statement.
In option (b), only one line can be drawn to pass through two given points. So, it is not a true statement.
In option (c),
'If two circles are equal, then their radii are equal' is the true statement.
In option (d), A line has no end points. A line has an indefinite length. So, it is not a true statement.
Solution 23
Correct option: (c)
Option (a) is true, since we can pass an infinite number of lines through a given point.
Option (b) is true, since a unique line can be drawn to pass through two given points.
Consider option (c).
As shown in the above diagram, a ray has only one end-point. So, option (d) is true.
Hence, the only false statement is option (c).
Solution 24
Correct option: (c)
A point C is called the midpoint of a line segment 
, if C is an interior point of AB such that 
=
.
Solution 25
Correct option: (d)
Observe the above figure. Clearly, C lies between A and B if AC + CB = AB.
That means, points A, B, C are collinear.
Solution 26
Correct option: (b)
Euclid's second axiom states that 'If equals are added to equals, the wholes are equal'.
Hence, when x + y = 15, then x + y + z = 15 + z.
Solution 27
Correct option: (a)
Euclid's first axiom states that 'Things which are equal to the same thing are equal to one another'.
That is,
A's age = B's age and C's age = B' age
⇒ A's age = C's age
Introduction to Euclid's Geometry Exercise Ex. 6
Solution 1
A theorem is a statement that requires a proof. Whereas, a basic fact which is taken for granted, without proof, is called an axiom.
Example of Theorem: Pythagoras Theorem
Example of axiom: A unique line can be drawn through any two points.
Solution 2
(i) Line segment: The straight path between two points is called a line segment.
(ii) Ray: A line segment when extended indefinitely in one direction is called a ray.
(iii) Intersecting Lines: Two lines meeting at a common point are called intersecting lines, i.e., they have a common point.
(iv) Parallel Lines: Two lines in a plane are said to be parallel, if they have no common point, i.e., they do not meet at all.
(v) Half-line: A ray without its initial point is called a half-line.
(vi) Concurrent lines: Three or more lines are said to be concurrent, if they intersect at the same point.
(vii) Collinear points: Three or more than three points are said to be collinear, if they lie on the same line.
(viii) Plane: A plane is a surface such that every point of the line joining any two points on it, lies on it.
Solution 3
(i) Six points: A,B,C,D,E,F
(ii)
Five line segments: 
(iii)
Four rays: 
(iv)
Four lines: 
(vi) Four collinear points: M,E,G,B
Solution 4
(i) 
and their corresponding point of intersection is R.
and their corresponding point of intersection is P.
(ii)
and their point of intersection is R.
(iii) Three rays are:
.
(iv) Two line segments are:
.
Solution 5
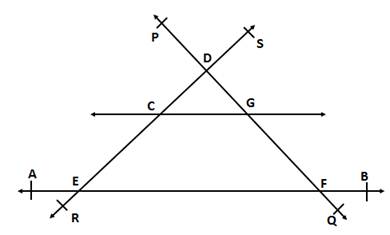
(i) Three lines: Line AB, Line PQ and Line RS
(ii) One rectilinear figure: EFGC
(iii) Four concurrent points: Points A, E, F and B
Solution 6
(i) An infinite number of lines can be drawn to pass through a given point.
(ii) One and only one line can pass through two given points.
(iii) Two given lines can at the most intersect at one and only one point.
(iv)
Solution 7
(i) False
(ii) False
(iii) False
(iv) True
(v) False
(vi) True
(vii) True
(viii) True
(ix) True
(x) True
(xi) False
(xii) True
Solution 8
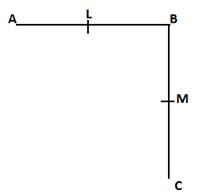
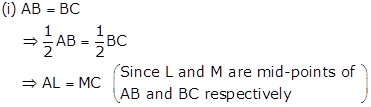
(ii) BL = BM
⇒ 2BL = 2BM
⇒ AB = BC