Class 9 R S AGGARWAL AND V AGGARWAL Solutions Maths Chapter 3 - Factorisation of Polynomials
Factorisation of Polynomials Exercise MCQ
Solution 1
Correct option: (c)
Let p(x) = 2x2 + kx
Since (x + 1) is a factor of p(x),
P(-1) = 0
⇒ 2(-1)2 + k(-1) = 0
⇒ 2 - k = 0
⇒ k = 2
Solution 2
Correct option: (d)
(249)2 - (248)2
= (249 + 248)(249 - 248)
= 497 × 1
= 497
Solution 3
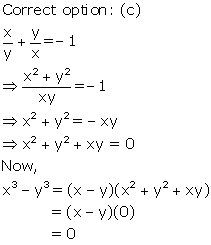
Solution 4
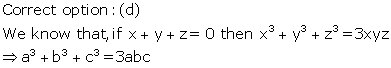
Solution 5
Correct option: (c)
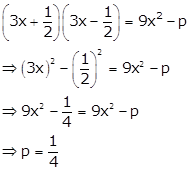
Solution 6

Solution 7
Correct option: (d)
(x + y)3 - (x3 + y3)
= (x + y)3 - [(x + y)(x2 - xy + y2)]
= (x + y)[(x + y)2 - (x2 - xy + y2)]
= (x + y)[x2 + y2 + 2xy - x2 + xy - y2]
= (x + y)(3xy)
Solution 8
Correct option: (d)
(25x2 - 1) + (1 + 5x)2
= [(5x)2 - (1)2] + (1 + 5x)2
= (5x - 1)(5x + 1) + (1 + 5x)2
= (1 + 5x)[(5x - 1) + (1 + 5x)]
= (1 + 5x)(5x - 1 + 1 + 5x)
= (1 + 5x)(10x)
Solution 9
Correct option: (b)
Since (x + 5) is a factor of p(x) = x3 - 20x + 5k,
p(-5) = 0
⇒ (-5)3 - 20(-5) + 5k = 0
⇒ -125 + 100 + 5k = 0
⇒ -25 + 5k = 0
⇒ 5k = 25
⇒ k = 5
Solution 10

Solution 11

Solution 12
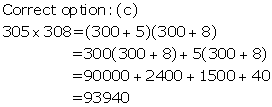
Solution 13
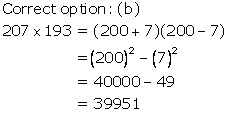
Solution 14

Solution 15
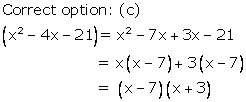
Solution 16

Solution 17
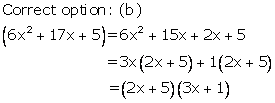
Solution 18

Solution 19
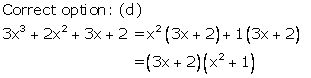
Solution 20
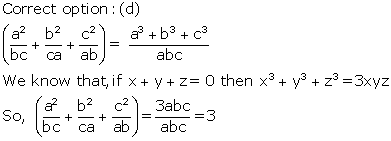
Solution 21
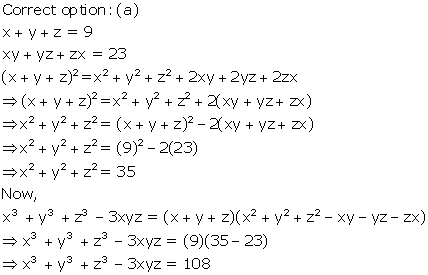
Solution 22
Correct option: (d)
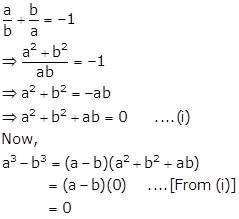
Factorisation of Polynomials Exercise Ex. 3C
Solution 1
x2 + 11x + 30
= x2 + 6x + 5x + 30
= x (x + 6) + 5 (x + 6)
= (x + 6) (x + 5).
Solution 2
x2 + 18x + 32
= x2 + 16x + 2x + 32
= x (x + 16) + 2 (x + 16)
= (x + 16) (x + 2).
Solution 3
x2 + 20x - 69
= x2 + 23x - 3x - 69
= x(x + 23) - 3(x + 23)
= (x + 23)(x - 3)
Solution 4
x2 + 19x - 150
= x2 + 25x - 6x - 150
= x(x + 25) - 6(x + 25)
= (x + 25)(x - 6)
Solution 5
x2 + 7x - 98
= x2 + 14x - 7x - 98
= x(x + 14) - 7(x + 14)
= (x + 14)(x - 7)
Solution 6
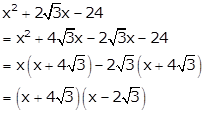
Solution 7
x2 - 21x + 90
= x2 - 6x - 15x + 90
= x(x - 6) - 15(x - 6)
= (x - 6)(x - 15)
Solution 8
x2 - 22x + 120
= x2 - 10x - 12x + 120
= x(x - 10) - 12(x - 10)
= (x - 10)(x - 12)
Solution 9
x2 - 4x + 3
= x2 - 3x - x + 3
= x(x - 3) - 1(x - 3)
= (x - 3)(x - 1)
Solution 10
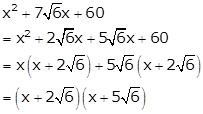
Solution 11
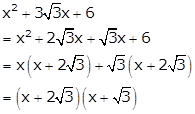
Solution 12
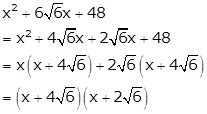
Solution 13
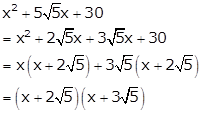
Solution 14
x2 - 24x - 180
= x2 - 30x + 6x - 180
= x(x - 30) + 6(x - 30)
= (x - 30)(x + 6)
Solution 15
z2 - 32z - 105
= z2 - 35z + 3z - 105
= z (z - 35) + 3 (z - 35)
= (z - 35) (z + 3)
Solution 16
x2 - 11x - 80
= x2 - 16x + 5x - 80
= x (x - 16) + 5 (x - 16)
= (x - 16) (x + 5).
Solution 17
6 - x - x2
= 6 + 2x - 3x - x2
= 2(3 + x) - x (3 + x)
= (3 + x) (2 - x).
Solution 18
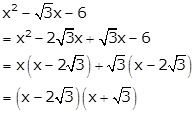
Solution 19
40 + 3x - x2
= 40 + 8x - 5x - x2
= 8 (5 + x) -x (5 + x)
= (5 + x) (8 - x).
Solution 20
x2 - 26x + 133
= x2 - 19x - 7x + 133
= x(x - 19) - 7(x - 19)
= (x - 19)(x - 7)
Solution 21
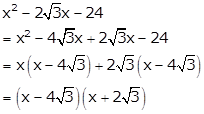
Solution 22
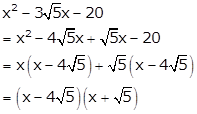
Solution 23
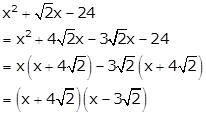
Solution 24
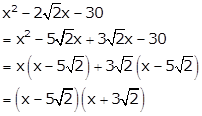
Solution 25
x2 - x - 156
= x2 - 13x + 12x - 156
= x (x - 13) + 12 (x - 13)
= (x - 13) (x + 12).
Solution 27
9x2 + 18x + 8
= 9x2 + 12x + 6x + 8
= 3x (3x+ 4) +2 (3x + 4)
= (3x + 4) (3x + 2).
Solution 28
6x2 + 17x + 12
= 6x2 + 9x + 8x + 12
= 3x (2x + 3) + 4(2x + 3)
= (2x + 3) (3x + 4).
Solution 29
18x2 + 3x - 10
= 18x2 - 12x + 15x - 10
= 6x (3x - 2) + 5 (3x - 2)
= (6x + 5) (3x - 2).
Solution 30
2x2 + 11x - 21
= 2x2 + 14x - 3x - 21
= 2x (x + 7) - 3 (x + 7)
= (x + 7) (2x - 3).
Solution 31
15x2 + 2x - 8
= 15x2 - 10x + 12x - 8
= 5x (3x - 2) + 4 (3x - 2)
= (3x - 2) (5x + 4).
Solution 32
21x2 + 5x - 6
= 21x2 + 14x - 9x - 6
= 7x(3x + 2) - 3(3x + 2)
= (3x + 2)(7x - 3)
Solution 33
24x2 - 41x + 12
= 24x2 - 32x - 9x + 12
= 8x (3x - 4) - 3 (3x - 4)
= (3x - 4) (8x - 3).
Solution 34
3x2 - 14x + 8
= 3x2 - 12x - 2x +8
= 3x (x - 4) - 2(x - 4)
= (x - 4) (3x - 2).
Solution 35
2x2 + 3x - 90
= 2x2 - 12x + 15x - 90
= 2x (x - 6) + 15 (x - 6)
= (x - 6) (2x + 15).
Solution 37
![]()
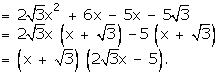
Solution 38
![]()
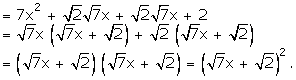
Solution 39
![]()
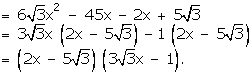
Solution 40
![]()
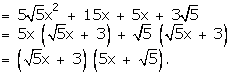
Solution 41
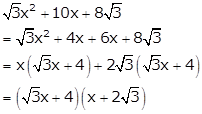
Solution 42
![]()
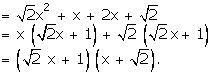
Solution 43
![]()
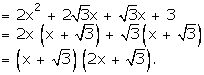
Solution 44
15x2 - x - 28
= 15x2 + 20x - 21x - 28
= 5x (3x + 4) - 7 (3x + 4)
= (3x + 4) (5x - 7).
Solution 45
6x2 - 5x - 21
= 6x2 + 9x - 14x - 21
= 3x (2x + 3) - 7 (2x + 3)
= (3x - 7) (2x + 3).
Solution 46
2x2 - 7x - 15
= 2x2 - 10x + 3x - 15
= 2x (x - 5) + 3 (x - 5)
= (x - 5) (2x + 3).
Solution 47
5x2 - 16x - 21
= 5x2 + 5x - 21x - 21
= 5x (x + 1) -21 (x + 1)
= (x + 1) (5x - 21).
Solution 48
6x2 - 11x - 35
= 6x2 - 21x + 10x - 35
= 3x(2x - 7) + 5(2x - 7)
= (2x - 7)(3x + 5)
Solution 49
9x2 - 3x - 20
= 9x2 - 15x + 12x - 20
= 3x(3x - 5) + 4(3x - 5)
= (3x - 5)(3x + 4)
Solution 50
10x2 - 9x - 7
= 10x2 + 5x - 14x - 7
= 5x (2x + 1) - 7 (2x+ 1)
= (2x + 1) (5x - 7).
Solution 51
x2 - 2x + ![]()

![]()
Solution 52
![]()

Solution 53
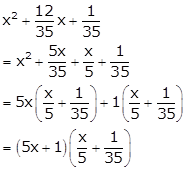
Solution 54
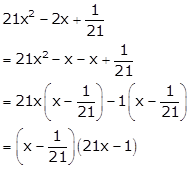
Solution 55
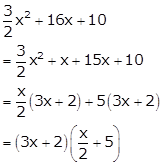
Solution 56
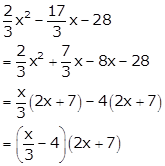
Solution 57
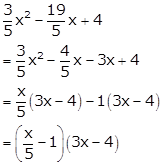
Solution 58
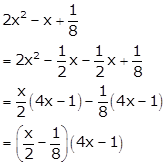
Solution 59
Letx + y = z
Then, 2 (x+ y)2 - 9 (x + y) - 5
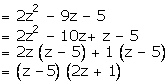
Now, replacing z by (x + y), we get
![]()
![]()
Solution 60
Let2a - b = c
Then,9 (2a - b)2 - 4 (2a - b) -13
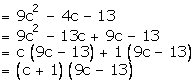
Now, replacing c by (2a - b) , we get
9 (2a - b)2 - 4 (2a - b) - 13
![]()
Solution 61
Let x - 2y = z
Then, 7 (x - 2y)2 - 25 (x - 2y) + 12
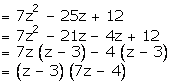
Now replace z by (x - 2y), we get
7 (x - 2y)2 - 25 (x - 2y) + 12
![]()
Solution 62
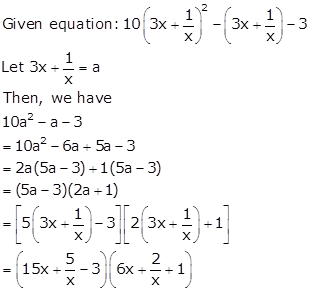
Solution 63
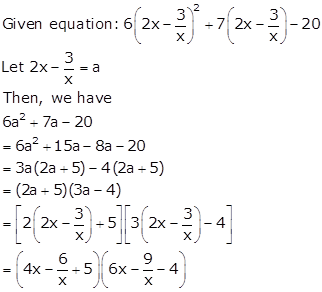
Solution 64
Given equation: (a + 2b)2 + 101(a + 2b) + 100
Let (a + 2b) = x
Then, we have
x2 + 101x + 100
= x2 + 100x + x + 100
= x(x + 100) + 1(x + 100)
= (x + 100)(x + 1)
= (a + 2b + 100)(a + 2b + 1)
Solution 65
Let x2 = y
Then, 4x4 + 7x2 - 2
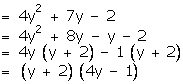
Now replacing y by x2, we get
![]()
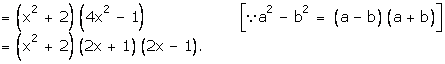
Solution 66
{(999)2 - 1}
= {(999)2 - (1)2}
= {(999 - 1)(999 + 1)}
= 998 × 1000
= 998000
Factorisation of Polynomials Exercise Ex. 3D
Solution 1(i)
We know:
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
(i) (a + 2b + 5c)2
= (a)2 + (2b)2 + (5c)2 + 2(a) (2b) + 2 (2b) (5c) + 2(5c) (a)
= a2 + 4b2 + 25c2 + 4ab + 20bc + 10ac
Solution 1(ii)
We know:
(2a - b + c)2
= (2a)2 + (-b)2 + (c)2 + 2 (2a) (-b) + 2(-b) (c) + 2 (c) (2a)
= 4a2 + b2 + c2 - 4ab - 2bc + 4ac.
Solution 1(iii)
We know:
(a - 2b - 3c)2
= (a)2 + (-2b)2 + (-3c)2+ 2(a) (-2b) + 2(-2b) (-3c) + 2 (-3c) (a)
= a2 + 4b2 + 9c2 - 4ab + 12bc - 6ac.
Solution 2(i)
We know:
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
(2a - 5b - 7c)2
= (2a)2 + (-5b)2 + (-7c)2 + 2 (2a) (-5b) + 2 (-5b) (-7c) + 2 (-7c) (2a)
= 4a2 + 25b2 + 49c2 - 20ab + 70bc - 28ac.
Solution 2(ii)
(-3a + 4b - 5c)2
= (-3a)2 + (4b)2 + (-5c)2 + 2 (-3a) (4b) + 2 (4b) (-5c) + 2 (-5c) (-3a)
= 9a2 + 16b2 + 25c2 - 24ab - 40bc + 30ac.
Solution 2(iii)
![]()
![]() =
= ![]()
Solution 3
4x2 + 9y2 + 16z2 + 12xy - 24yz - 16xz
= (2x)2 + (3y)2 + (-4z)2 + 2 (2x) (3y) + 2(3y) (-4z) + 2 (-4z) (2x)
= (2x + 3y - 4z)2
Solution 4
9x2 + 16y2 + 4z2 - 24xy + 16yz - 12xz
= (-3x)2 + (4y)2 + (2z)2 + 2 (-3x) (4y) + 2 (4y) (2z) + 2 (2z) (-3x)
= (-3x + 4y + 2z)2.
Solution 5
25x2 + 4y2 + 9z2 - 20xy - 12yz + 30xz
= (5x)2 + (-2y)2 + (3z)2 + 2(5x) (-2y) + 2(-2y) (3z) + 2(3z) (5x)
= (5x - 2y + 3z)2
Solution 6
16x2 + 4y2 + 9z2 - 16xy - 12yz + 24xz
= (4x)2 + (-2y)2 + (3z)2 + 2(4x)(-2y) + 2(-2y)(3z) + 2(4x)(3z)
= [4x + (-2y) + 3z]2
= (4x - 2y + 3z)2
= (4x - 2y + 3z)(4x - 2y + 3z)
Solution 7(i)
(99)2
= (100 - 1)2![]()
= (100)2 - 2(100) (1) + (1)2
= 10000 - 200 + 1
= 9801.
Solution 7(ii)
(995)2
= (1000 - 5)2
= (1000)2 + (5)2 - 2(1000)(5)
= 1000000 + 25 - 10000
= 990025
Solution 7(iii)
(107)2
= (100 + 7)2
= (100)2 + (7)2 + 2(100)(7)
= 10000 + 49 + 1400
= 11449
Factorisation of Polynomials Exercise Ex. 3E
Solution 1(i)
(3x + 2)3
= (3x)3 + (2)3 + 3 ![]() 3x
3x ![]() 2 (3x + 2)
2 (3x + 2)
![]()
= 27x3 + 8 + 18x (3x + 2)
= 27x3 + 8 + 54x2 + 36x.
Solution 1(ii)
![]()

Solution 1(iii)
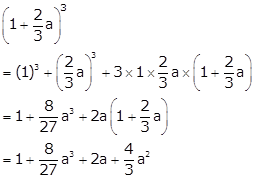
Solution 2(i)
(5a - 3b)3
= (5a)3 - (3b)3 - 3(5a)(3b)(5a - 3b)
= 125a3 - 27b3 - 45ab(5a - 3b)
= 125a3 - 27b3 - 225a2b + 135ab2
Solution 2(ii)
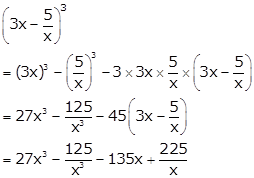
Solution 2(iii)
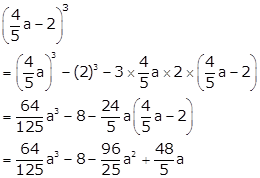
Solution 3
8a3 + 27b3 + 36a2b + 54ab2
= (2a)3 + (3b)3 + 3 × (2a)2 × (3b) + 3 × (2a) × (3b)2
= (2a + 3b)3
= (2a + 3b)(2a + 3b)(2a + 3b)
Solution 4
64a3 - 27b3 - 144a2b + 108ab2
= (4a)3 - (3b)3 - 3 × (4a)2 × (3b) + 3 × (4a) × (3b)2
= (4a - 3b)3
= (4a - 3b)(4a - 3b)(4a - 3b)
Solution 5
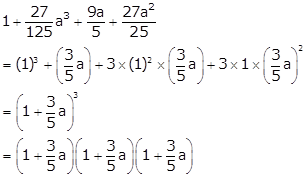
Solution 6
125x3 - 27y3 - 225x2y + 135xy2
= (5x)3 - (3y)3 - 3 × (5x)2 × (3y) + 3 × (5x) × (3y)2
= (5x - 3y)3
= (5x - 3y)(5x - 3y)(5x - 3y)
Solution 7
a3x3 - 3a2bx2 + 3ab2x - b3
= (ax)3 - 3 × (ax)2 × b + 3 × (ax) × (b)2 - (b)3
= (ax - b)3
= (ax - b)(ax - b)(ax - b)
Solution 8
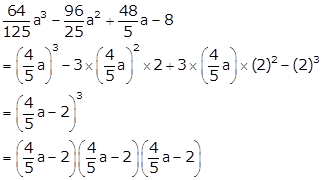
Solution 9
a3 - 12a(a - 4) - 64
= a3 - 3 × a × 4(a - 4) - (4)3
= (a - 4)3
= (a - 4)(a - 4)(a - 4)
Solution 10(i)
(103)3
= (100 + 3)3
= (100)3 + (3)3 + 3 × 100 × 3 × (100 + 3)
= 1000000 + 27 + 900(103)
= 1000000 + 27 + 92700
= 1092727
Solution 10(ii)
(99)3
= (100 - 1)3
= (100)3 - (1)3 - 3 × 100 × 1 × (100 - 1)
= 1000000 - 1 - 300(99)
= 1000000 - 1 - 29700
= 970299
Factorisation of Polynomials Exercise Ex. 3F
Solution 1
x3 + 27
= x3 + 33
= (x + 3) (x2 - 3x + 9)
![]()
Solution 2
27a3 + 64b3
= (3a)3 + (4b)3
= (3a + 4b)[(3a)2 - (3a)(4b) + (4b)2]
= (3a + 4b)(9a2 - 12ab + 16b2)
Solution 3
125a3 + ![]()
We know that ![]()
Let us rewrite
![]()

Solution 4
216x3 + ![]()
We know that ![]()
Let us rewrite
![]()

Solution 5
16x 4 + 54x
= 2x (8x 3 + 27)
= 2x [(2x)3 + (3)3]
= 2x (2x + 3) [(2x)2 - 2x![]() 3 + 32]
3 + 32] ![]()
=2x(2x+3)(4x2 -6x +9)
Solution 6
7a3 + 56b3
= 7(a3 + 8b3)
= 7 [(a)3 + (2b)3]
= 7 (a + 2b) [a2 - a ![]() 2b + (2b)2]
2b + (2b)2] ![]()
= 7 (a + 2b) (a2 - 2ab + 4b2).
Solution 7
x5 + x2
= x2(x3 + 1)
= x2 (x + 1) [(x)2 - x ![]() 1 + (1)2]
1 + (1)2] ![]()
= x2 (x + 1) (x2 - x + 1).
Solution 8
a3 + 0.008
= (a)3 + (0.2)3
= (a + 0.2) [(a)2 - a ![]() 0.2 + (0.2)2]
0.2 + (0.2)2] ![]()
= (a + 0.2) (a2 - 0.2a + 0.04).
Solution 9
1 - 27x3
= (1)3 - (3x)3
= (1 - 3x) [(1)2 + 1 ![]() 3x + (3x)2]
3x + (3x)2] ![]()
= (1 - 3x) (1 + 3x + 9x2).
Solution 10
64a3 - 343
= (4a)3 - (7)3
= (4a - 7)[(4a)2 + (4a)(7) + (7)2]
= (4a - 7)(16a2 + 28a + 49)
Solution 11
x3 - 512
= (x)3 - (8)3
= (x - 8) [(x)2 + x ![]() 8 + (8)2]
8 + (8)2] ![]()
= (x - 8) (x2 + 8x + 64).
Solution 12
a3 - 0.064
= (a)3 - (0.4)3
= (a- 0.4) [(a)2 + a ![]() 0.4 + (0.4)2]
0.4 + (0.4)2] ![]()
= (a - 0.4) (a2 + 0.4 a + 0.16).
Solution 13
We know that ![]()
Let us rewrite
![]()

Solution 14
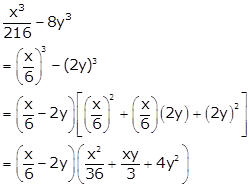
Solution 15
x - 8xy3
= x (1 - 8y3)
= x [(1)3 - (2y)3]
= x (1 - 2y) [(1)2 + 1 ![]() 2y + (2y)2]
2y + (2y)2] ![]()
= x (1 - 2y) (1 + 2y + 4y2).
Solution 16
32x4 - 500x
= 4x (8x3 - 125)
= 4x [(2x)3 - (5)3]
= 4x [(2x - 5) [(2x)2 + 2x ![]() 5 + (5)2]
5 + (5)2] ![]()
= 4x (2x - 5) (4x2 + 10x + 25).
Solution 17
3a7b - 81a4b4
= 3a4b (a3 - 27b3)
= 3a4b [(a)3 - (3b)3]
= 3a4b (a - 3b) [(a)2 + a ![]() 3b + (3b)2]
3b + (3b)2] ![]()
= 3a4b (a - 3b) (a2 + 3ab + 9b2).
Solution 18
x4y4 - xy
= xy(x3y3 - 1)
= xy[(xy)3 - (1)3]
= xy{(xy - 1)[(xy)2 + (xy)(1) + (1)2]}
= xy(xy - 1)(x2y2 + xy + 1)
Solution 19
8x2y3 - x5
= x2 (8y3 - x3)
= x2 [(2y)3 - x3]
= x2 [(2y - x)[(2y)2 + (2y)(x) + x2]
= x2 (2y - x)(4y2 + 2xy + x2)
Solution 20
1029 - 3x3
= 3(343 - x3)
= 3[(7)3 - x3]
= 3[(7 - x)(72 + 7x + x2)]
= 3(7 - x)(49 + 7x + x2)
Solution 21
x6 - 729
= (x2)3 - (9)3
= (x2 - 9) [(x2)2 + x2 ![]() 9 + (9)2]
9 + (9)2] ![]()
= (x2 - 9) (x4 + 9x2 + 81)
= (x + 3) (x - 3) [(x2 + 9)2 - (3x)2]
= (x + 3) (x - 3) (x2 + 3x + 9) (x2 - 3x + 9).
Solution 22
x9 - y9
= (x3)3 - (y3)3
= [(x3 - y3)][(x3)2 + x3y3 + (y3)2]
= [(x - y)(x2 + xy + y2)(x6 + x3y3 + y6)
Solution 23
We know that, ![]()
Therefore,
(a + b)3 - (a - b)3
= [a + b - (a - b)] [ (a + b)2 + (a + b) (a - b) + (a - b)2]
= (a + b - a + b) [ a2 + b2 + 2ab + a2 - b2 + a2 + b2 - 2ab]
= 2b (3a2 + b2).
Solution 24
8a3 - b3 - 4ax + 2bx
= 8a3 - b3 - 2x (2a - b)
= (2a)3 - (b)3 - 2x (2a - b)
= (2a - b) [(2a)2 + 2a ![]() b + (b)2] - 2x (2a - b)
b + (b)2] - 2x (2a - b) ![]()
= (2a - b) (4a2 + 2ab + b2) - 2x (2a - b)
= (2a - b) (4a2 + 2ab + b2 - 2x).
Solution 25

Solution 26
We know that ![]()
![]()
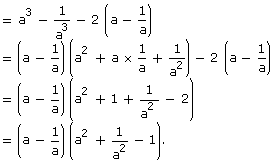
Solution 27
2a3 + 16b3 - 5a - 10b
= 2 (a3 + 8b3) - 5 (a + 2b)
= 2 [(a)3 + (2b)3] - 5 (a + 2b)
= 2 (a + 2b) [(a)2 - a ![]() 2b + (2b)2 ] - 5 (a + 2b)
2b + (2b)2 ] - 5 (a + 2b) ![]()
= (a+ 2b) [2(a2 - 2ab + 4b2) - 5]
Solution 28
a6 + b6
= (a2)3 + (b2)3
= (a2 + b2)[(a2)2 - (a2b2) + (b2)2]
= (a2 + b2)(a4 - a2b2 + b4)
Solution 29
a12 - b12
= (a6)2 - (b6)2
= (a6 - b6)(a6 + b6)
= [(a3)2 - (b3)2][(a2)3 + (b2)3]
= (a3 - b3)(a3 + b3)[(a2 + b2)(a4 - a2b2 + b4)]
= (a - b)(a2 + ab + b2)(a + b)(a2 - ab + b2)(a2 + b2)(a4 - a2b2 + b4)
= (a - b)(a + b)(a2 + b2)(a2 + ab + b2)(a2 - ab + b2)(a4 - a2b2 + b4)
Solution 30
Given equation is x6 - 7x3 - 8.
Putting x3 = y, we get
y2 - 7y - 8
= y2 - 8y + y - 8
= y(y - 8) + 1(y - 8)
= (y - 8)(y + 1)
= (x3 - 8)(x3 + 1)
= (x3 - 23)(x3 + 13)
= (x - 2)(x2 + 2x + 4)(x + 1)(x2 - x + 1)
= (x - 2)(x + 1)(x2 + 2x + 4)(x2 - x + 1)
Solution 31
x3 - 3x2 + 3x + 7
= x3 - 3x2 + 3x - 1 + 8
= (x3 - 3x2 + 3x - 1) + 8
= (x - 1)3 + 23
= (x - 1 + 2)[(x - 1)2 - (x - 1)(2) + 22]
= (x + 1)(x2 - 2x + 1 - 2x + 2 + 4)
= (x + 1)(x2 - 4x + 7)
Solution 32
(x + 1)3 + (x - 1)3
= (x + 1 + x - 1)[(x + 1)2 - (x + 1)(x - 1) + (x - 1)2]
= 2x(x2 + 2x + 1 - x2 + 1 + x2 - 2x + 1)
= 2x(x2 + 3)
Solution 33
(2a + 1)3 + (a - 1)3
= (2a + 1 + a - 1)[(2a + 1)2 - (2a + 1)(a - 1) + (a - 1)2]
= (3a)[4a2 + 4a + 1 - 2a2 + 2a - a + 1 + a2 - 2a + 1]
= 3a(3a2 + 3a + 3)
= 9a(a2 + a + 1)
Solution 34
8(x + y)3 - 27(x - y)3
= [23 (x + y)3] - [33 (x - y)3]
= [2(x + y) - 3(x - y)]{[2(x + y)]2 + 2(x + y)3(x - y) + [3(x - y)]2}
= (2x + 2y - 3x + 3y){[4(x2 + y2 + 2xy)] + 6(x2 - y2) + [9(x2 + y2 - 2xy]}
= (-x + 5y){4x2 + 4y2 + 8xy + 6x2 - 6y2 + 9x2 + 9y2 - 18xy}
= (-x + 5y)(19x2 + 7y2 - 10xy)
Solution 35
(x + 2)3 + (x - 2)3
= [(x + 2) + (x - 2)][(x + 2)2 - (x + 2)(x - 2) + (x - 2)2]
=(2x)(x2 + 4x + 4 - x2 + 4 + x2 - 4x + 4)
= 2x(x2 + 12)
Solution 36
(x + 2)3 - (x - 2)3
= [(x + 2) - (x - 2)][(x + 2)2 + (x + 2)(x - 2) + (x - 2)2]
= 4(x2 + 4x + 4 + x2 - 4 + x2 - 4x + 4)
= 4(3x2 + 4)
Solution 37
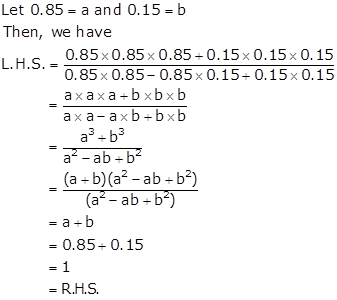
Solution 38
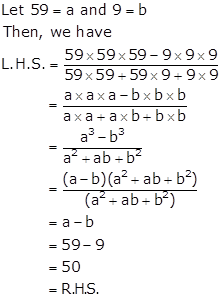
Factorisation of Polynomials Exercise Ex. 3G
Solution 1
(x + y - z) (x2 + y2 + z2 - xy + yz + zx)
= [x + y + (-z)] [(x)2 + (y)2 + (-z)2 - (x) (y) - (y) (-z) - (-z) (x)]
= x3 + y3 - z3 + 3xyz.
Solution 2
(x - y - z)(x2 + y2 + z2 + xy - yz + xz)
= x3 + xy2 + xz2 + x2y - xyz + x2z - x2y - y3 - yz2 - xy2 + y2z - xyz - x2z - y2z - z3 - xyz + yz2 - xz2
= x3 - y3 - z3 - xyz - xyz - xyz
= x3 - y3 - z3 - 3xyz
Solution 3
(x - 2y + 3) (x2 + 4y2 + 2xy - 3x + 6y + 9)
= [x + (-2y) + 3] [(x)2 + (-2y)2 + (3) - (x) (-2y) - (-2y) (3) - (3) (x)]
= (a + b + c) (a2 + b2 + c2 - ab - bc - ca)
= a3 + b3 + c3 - 3abc
Where, x = a, (-2y) = b and 3 = c
![]() (x
- 2y + 3) (x2 + 4y2 + 2xy - 3x + 6y + 9)
(x
- 2y + 3) (x2 + 4y2 + 2xy - 3x + 6y + 9)
= (x)3 + (-2y)3 + (3)2 - 3 (x) (-2y) (3)
= x3 - 8y3 + 27 + 18xy.
Solution 4
(3x - 5y + 4)(9x2 + 25y2 + 15xy + 20y - 12x + 16)
= (3x + (-5y) + 4)[(3x)2 + (-5y)2 + (4)2 - (3x)(-5y) - (-5y)(4) - (3x)(4)]
= (3x)3 + (-5y)3 + (4)3 - 3(3x)(-5y)(4)
= 27x3 - 125y3 + 64 + 180xy
Solution 5
125a3 + b3 + 64c3 - 60abc
= (5a)3 + (b)3 + (4c)3 - 3 (5a) (b) (4c)
= (5a + b + 4c) [(5a)2 + b2 + (4c)2 - (5a) (b) - (b) (4c) - (5a) (4c)]
[![]() a3 + b3 + c3 - 3abc = (a+ b + c) (a2 + b2 + c2 - ab - bc - ca)]
a3 + b3 + c3 - 3abc = (a+ b + c) (a2 + b2 + c2 - ab - bc - ca)]
= (5a + b + 4c) (25a2 + b2 + 16c2 - 5ab - 4bc - 20ac).
Solution 6
a3 + 8b3 + 64c3 - 24abc
= (a)3 + (2b)3 + (4c)3 - 3 ![]() a
a ![]() 2b
2b ![]() 4c
4c
= (a + 2b + 4c) [a2 + 4b2 + 16c2 - 2ab - 8bc - 4ca).
Solution 7
1 + b3 + 8c3 - 6bc
= 1 + (b)3 + (2c)3 - 3 (b) (2c)
= (1 + b + 2c) [1 + b2 + (2c)2 - b - b ![]() 2c - 2c]
2c - 2c]
= (1 + b + 2c) (1 + b2 + 4c2 - b - 2bc - 2c).
Solution 8
216 + 27b3 + 8c3 - 108bc
= (6)3 + (3b)3 + (2c)2 - 3 ![]() 6
6 ![]() 3b
3b ![]() 2c
2c
= (6 + 3b + 2c) [(6)2 + (3b)2 + (2c)2 - 6 ![]() 3b - 3b
3b - 3b ![]() 2c - 2c
2c - 2c ![]() 6]
6]
= (6 + 3b + 2c) (36 + 9b2 + 4c2 - 18b - 6bc - 12c).
Solution 9
27a3 - b3 + 8c3 + 18abc
= (3a)3 + (-b)3 + (2c)3 + 3(3a) (-b) (2c)
= [3a + (-b) + 2c] [(3a)2 + (-b)2 + (2c)2 - 3a ![]() (-b) - (-b) (2c) - (2c) (3a)]
(-b) - (-b) (2c) - (2c) (3a)]
= (3a - b + 2c) (9a2 + b2 + 4c2 + 3ab + 2bc - 6ca).
Solution 10
8a3 + 125b3 - 64c3 + 120abc
= (2a)3 + (5b)3 + (-4c)3 - 3 (2a) (5b) (-4c)
= (2a + 5b - 4c) [(2a)2 + (5b)2 + (-4c)2 - (2a) (5b) - (5b) (-4c) - (-4c) (2a)]
= (2a + 5b - 4c) (4a2 + 25b2 + 16c2 - 10ab + 20bc + 8ca).
Solution 11
8 - 27b3 - 343c3 - 126bc
= (2)3 + (-3b)3 + (-7c)3 - 3(2) (-3b) (-7c)
= (2 - 3b - 7c) [(2)2 + (-3b)2 + (-7c)2 - (2) (-3b) - (-3b) (-7c) - (-7c) (2)]
= (2 - 3b - 7c) (4 + 9b2 + 49c2 + 6b - 21bc + 14c).
Solution 12
125 - 8x3 - 27y3 - 90xy
= (5)3 + (-2x)3 + (-3y)3 - 3 (5) (-2x) (-3y)
= (5 - 2x - 3y) [(5)2 + (-2x)2 + (-3y)2 - (5) (-2x) - (-2x) (-3y) - (-3y) (5)]
= (5 - 2x - 3y) (25 + 4x2 + 9y2 + 10x - 6xy + 15y).
Solution 13
![]()
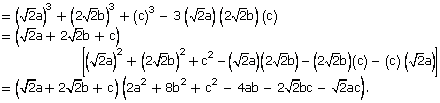
Solution 14
27x3 - y3 - z3 - 9xyz
= (3x)3 - y3 - z3 - 3(3x)(y)(z)
= (3x)3 + (-y)3 + (-z)3 - 3(3x)(-y)(-z)
= [3x + (-y) + (-z)][(3x)2 + (-y)2 + (-z)2 - (3x)(-y) - (-y)(-z) - (3x)(-z)]
= (3x - y - z)(9x2 + y2 + z2 + 3xy - yz + 3zx)
Solution 15
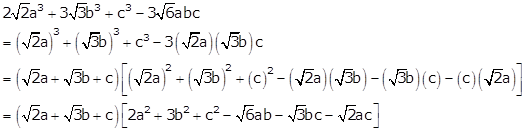
Solution 16
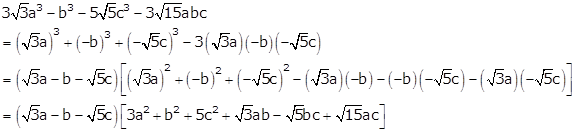
Solution 17
Putting (a - b) = x, (b - c) = y and (c - a) = z, we get,
(a - b)3 + (b - c)3 + (c - a)3
= x3 + y3 + z3, where (x + y + z) = (a - b) + (b - c) + (c - a) = 0
= 3xyz[![]() (x + y + z)= 0
(x + y + z)= 0 ![]() (x3 + y3 + z3) = 3xyz]
(x3 + y3 + z3) = 3xyz]
= 3(a - b) (b - c) (c - a).
Solution 18
Given equation is (a - 3b)3 + (3b - c)3 + (c - a)3
Now,
(a - 3b) + (3b - c) + (c - a)
= a - a - 3b + 3b - c + c
= 0
We know that if x + y + z = 0, then x3 + y3 + z3 = 3xyz
Hence,
(a - 3b)3 + (3b - c)3 + (c - a)3
= 3(a - 3b)(3b - c)(c - a)
Solution 19
We have:
(3a - 2b) + (2b - 5c) + (5c - 3a) = 0
So, (3a - 2b)3 + (2b - 5c)3 + (5c - 3a)3
= 3(3a - 2b) (2b - 5c) (5c - 3a).
Solution 20
Given equation is (5a - 7b)3 + (7b - 9c)3 + (9c - 5a)3
Now,
(5a - 7b) + (7b - 9c) + (9c - 5a)
= 5a - 7b + 7b - 9c + 9c - 5a
= 0
We know that if x + y + z = 0, then x3 + y3 + z3 = 3xyz
Hence,
(5a - 7b)3 + (7b - 9c)3 + (9c - 5a)3
= 3(5a - 7b)(7b - 9c)(9c - 5a)
Solution 21
a3 (b - c)3 + b3 (c - a)3 + c3 (a - b)3
= [a (b - c)]3 + [b (c - a)]3 + [c (a - b)]3
Now, since, a (b - c) + b (c -a) + c (a - b)
= ab - ac + bc - ba + ca - bc = 0
So, a3 (b - c)3 + b3 (c - a)3 + c3 (a - b)3
= 3a (b - c) b (c - a) c (a - b)
= 3abc (a - b) (b - c) (c - a).
Solution 22(i)
Given equation is (-12)3 + 73 + 53
Now,
-12 + 7 + 5 = -12 + 12 = 0
We know that if x + y + z = 0, then x3 + y3 + z3 = 3xyz
Hence,
(-12)3 + 73 + 53
= 3(-12)(7)(5)
= -1260
Solution 22(ii)
Given equation is (28)3 + (-15)3 + (-13)3
Now,
28 + (-15) + (-13) = 28 - 28 = 0
We know that if x + y + z = 0, then x3 + y3 + z3 = 3xyz
Hence,
(28)3 + (-15)3 + (-13)3
= 3(28)(-15)(-13)
= 16380
Solution 23
L.H.S. = (a + b + c)3 - a3 - b3 - c3
= [(a + b) + c]3 - a3 - b3 - c3
= (a + b)3 + c3 + 3(a + b)c × [(a + b) + c] - a3 - b3 - c3
= a3 + b3 + 3ab(a + b) + c3 + 3(a + b)c × [(a + b) + c] - a3 - b3 - c3
= 3ab(a + b) + 3(a + b)c × [(a + b) + c]
= 3(a + b)[ab + c(a + b) + c2]
= 3(a + b)[ab + ac + bc + c2]
= 3(a + b)[a(b + c) + c(b + c)]
= 3(a + b)[(b + c)(a + c)]
= 3(a + b)(b + c)(c + a)
= R.H.S.
Solution 24
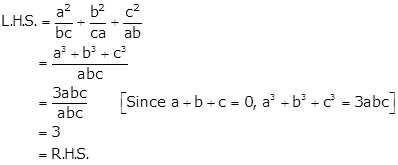
Solution 25
a3 + b3 + c3 - 3abc = (a + b + c)(a2 + b2 + c2 - ab - bc - ca)
= (a + b + c)[(a2 + b2 + c2) - (ab + bc + ca)] ….(i)
Now,
(a + b + c)2 = a2 + b2 + c2 + 2(ab + bc + ca)
⇒ (9)2 = 35 + 2(ab + bc + ca)
⇒ 81 = 35 + 2(ab + bc + ca)
⇒ 2(ab + bc + ca) = 46
⇒ ab + bc + ca = 23
Substituting in (i), we get
a3 + b3 + c3 - 3abc = (9)[35 - 23] = 9 × 12 = 108
Factorisation of Polynomials Exercise Ex. 3B
Solution 1
9x2 - 16y2
= (3x)2 - (4y)2
= (3x + 4y)(3x - 4y)
Solution 2
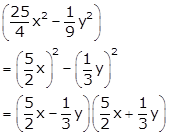
Solution 3
81 - 16x2
= (9)2 - (4x)2
= (9 - 4x)(9 + 4x)
Solution 4
5 - 20x2
= 5(1 - 4x2)
= 5[(1)2 - (2x)2]
= 5[(1 - 2x)(1 + 2x)]
= 5(1 - 2x)(1 + 2x)
Solution 5
2x4 - 32
= 2(x4 - 16)
= 2[(x2)2 - (4)2]
= 2[(x2 - 4)(x2 + 4)]
= 2[(x2 - 22)(x2 + 4)]
= 2[(x - 2)(x + 2)(x2 + 4)]
= 2(x - 2)(x + 2)(x2 + 4)
Solution 6
3a3b - 243ab3
= 3ab (a2 - 81 b2)
= 3ab [(a)2 - (9b)2]
= 3ab (a + 9b) (a - 9b)![]()
Solution 7
3x3 - 48x
= 3x (x2 - 16)
= 3x [(x)2 - (4)2]
= 3x (x + 4) (x - 4)![]()
Solution 8
27a2 - 48b2
= 3 (9a2 - 16b2)
= 3 [(3a)2 - (4b)2]
= 3(3a + 4b) (3a - 4b)![]()
Solution 9
x - 64x3
= x (1 - 64x2)
= x[(1)2 - (8x)2]
= x (1 + 8x) (1 - 8x)![]()
Solution 10
8ab2 - 18a3
= 2a (4b2 - 9a2)
= 2a [(2b)2 - (3a)2]
= 2a (2b + 3a) (2b - 3a)![]()
Solution 11
150 - 6x2
= 6 (25 - x2)
= 6 (52 - x2)
= 6 (5 + x) (5 - x)![]()
Solution 12
2 - 50x2
= 2 (1 - 25x2)
= 2 [(1)2 - (5x)2]
= 2 (1 + 5x) (1 - 5x)![]()
Solution 13
20x2 - 45
= 5(4x2 - 9)
= 5 [(2x)2 - (3)2]
= 5 (2x + 3) (2x - 3)![]()
Solution 14
(3a + 5b)2 - 4c2
= (3a + 5b)2 - (2c)2
= (3a + 5b - 2c)(3a + 5b + 2c)
Solution 15
a2 - b2 - a - b
= a2 - b2 - (a + b)
= (a - b)(a + b) - (a + b)
= (a + b)(a - b - 1)
Solution 16
4a2 - 9b2 - 2a - 3b
= (2a)2 - (3b)2 - (2a + 3b)
= (2a - 3b)(2a + 3b) - (2a + 3b)
= (2a + 3b)(2a - 3b - 1)
Solution 17
a2 - b2 + 2bc - c2
= a2 - (b2 - 2bc + c2)
= a2 - (b - c)2
= [a - (b - c)][a + (b - c)]
= (a - b + c)(a + b - c)
Solution 18
4a2 - 4b2 + 4a + 1
= (4a2 + 4a + 1) - 4b2
= [(2a)2 + 2 × 2a × 1 + (1)2] - (2b)2
= (2a + 1)2 - (2b)2
= (2a + 1 - 2b)(2a + 1 + 2b)
= (2a - 2b + 1)(2a + 2b + 1)
Solution 19
a2 + 2ab + b2 - 9c2
= (a + b)2 - (3c)2
= (a + b + 3c) (a + b - 3c)![]()
Solution 20
108a2 - 3(b - c)2
= 3 [(36a2 - (b -c)2]
= 3 [(6a)2 - (b - c)2]
= 3 (6a + b - c) (6a - b + c)![]()
Solution 21
(a + b)3 - a - b
= (a + b)3 - (a + b)
= (a + b) [(a + b)2 - 12]
= (a + b) (a + b + 1) (a + b - 1)![]()
Solution 22
x2 + y2 - z2 - 2xy
= (x2 + y2 - 2xy) - z2
= (x - y)2 - z2
= (x - y - z)(x - y + z)
Solution 23
x2 + 2xy + y2 - a2 + 2ab - b2
= (x2 + 2xy + y2) - (a2 - 2ab + b2)
= (x + y)2 - (a - b)2
= [(x + y) - (a - b)][(x + y) + (a - b)]
= (x + y - a + b)(x + y + a - b)
Solution 24
25x2 - 10x + 1 - 36y2
= (25x2 - 10x + 1) - 36y2
= [(5x)2 - 2(5x)(1) + (1)2] - (6y)2
= (5x - 1)2 - (6y)2
= (5x - 1 - 6y)(5x - 1 + 6y)
Solution 25
a - b - a2 + b2
= (a - b) - (a2 - b2)
= (a - b) - (a - b) (a + b)![]()
= (a - b) (1 - a - b)
Solution 26
a2 - 4ac + 4c2 - b2
= a2 - 4ac + 4c2 - b2
= a2 - 2 ![]() a
a ![]() 2c + (2c)2 - b2
2c + (2c)2 - b2
= (a - 2c)2 - b2
= (a - 2c + b) (a - 2c - b)![]()
Solution 27
9 - a2 + 2ab - b2
= 9 - (a2 - 2ab + b2)
= 32 - (a - b)2
= (3 + a - b) (3 - a + b)![]()
Solution 28
x3 - 5x2 - x + 5
= x2 (x - 5) - 1 (x - 5)
= (x - 5) (x2 - 1)
= (x - 5) (x + 1) (x - 1)![]()
Solution 29
1 + 2ab - (a2 + b2)
= 1 - (a2 + b2 - 2ab)
= (1)2 - (a - b)2
= [1 - (a - b)][1 + (a - b)]
= (1 - a + b)(1 + a - b)
Solution 30
9a2 + 6a + 1 - 36b2
= (9a2 + 6a + 1) - 36b2
= [(3a)2 + 2(3a)(1) + (1)2] - (6b)2
= (3a + 1)2 - (6b)2
= (3a + 1 - 6b)(3a + 1 + 6b)
Solution 31
x2 - y2 + 6y - 9
= x2 - (y2 - 6y + 9)
= x2 - (y2 - 2 ![]() y
y ![]() 3 + 32)
3 + 32)
= x2 - (y - 3)2
= [x + (y - 3)] [x - (y - 3)] ![]()
= (x + y - 3) (x - y + 3)
Solution 32
4x2 - 9y2 - 2x - 3y
= (2x)2 - (3y)2 - (2x + 3y)
= (2x + 3y) (2x - 3y) - (2x + 3y) ![]()
= (2x + 3y) (2x - 3y - 1)
Solution 33
9a2 + 3a - 8b - 64b2
= 9a2 - 64b2 + 3a - 8b
= (3a)2 - (8b)2 + (3a - 8b)
= (3a + 8b) (3a - 8b) + (3a - 8b)![]()
= (3a - 8b) (3a + 8b + 1)
Solution 34
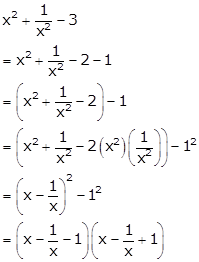
Solution 35
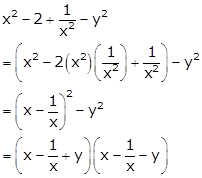
Solution 36
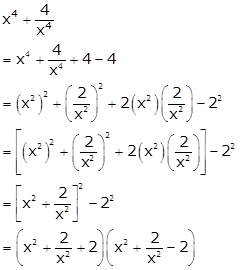
Solution 37
x8 - 1
= (x4)2 - (1)2
= (x4 - 1)(x4 + 1)
= [(x2)2 - (1)2)(x4 + 1)
= (x2 - 1)(x2 + 1)(x4 + 1)
= (x - 1)(x + 1)(x2 + 1)[(x2)2 + (1)2 + 2x2 - 2x2
= (x - 1)(x + 1)(x2 + 1)[(x2)2 + (1)2 + 2x2) - 2x2
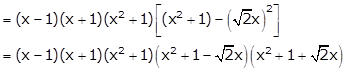
Solution 38
16x4 - 1
= (4x2)2 - (1)2
= (4x2 - 1)(4x2 + 1)
= [(2x)2 - (1)2](4x2 + 1)
= (2x - 1)(2x + 1)(4x2 + 1)
Solution 39
81x4 - y4
= (9x2)2 - (y2)2
= (9x2 - y2)(9x2 + y2)
= [(3x)2 - y2](9x2 + y2)
= (3x - y)(3x + y)(9x2 + y2)
Solution 40
x4 - 625
= (x2)2 - (25)2
= (x2 + 25) (x2 - 25)![]()
= (x2 + 25) (x2 - 52)
= (x2 + 25) (x + 5) (x - 5)![]()
Factorisation of Polynomials Exercise Ex. 3A
Solution 1
9x2 + 12xy = 3x (3x + 4y)
Solution 2
18x2y - 24xyz = 6xy (3x - 4z)
Solution 3
27a3b3 - 45a4b2 = 9a3b2 (3b - 5a)
Solution 4
2a (x + y) - 3b (x + y) = (x + y) (2a - 3b)
Solution 5
2x (p2 + q2) + 4y (p2 + q2)
= (2x + 4y) (p2 + q2)
= 2(x+ 2y) (p2 + q2)
Solution 6
x (a - 5) + y (5 - a)
= x (a - 5) + y (-1) (a - 5)
= (x - y) (a - 5)
Solution 7
4 (a + b) - 6 (a + b)2
= (a + b) [4 - 6 (a + b)]
= 2 (a + b) (2 - 3a - 3b)
= 2 (a + b) (2 - 3a - 3b)
Solution 8
8 (3a - 2b)2 - 10 (3a - 2b)
= (3a - 2b) [8(3a - 2b) - 10]
= (3a - 2b) 2[4 (3a - 2b) - 5]
= 2 (3a - 2b) (12 a - 8b - 5)
Solution 9
x (x + y)3 - 3x2y (x + y)
= x (x + y) [(x + y)2 - 3xy]
= x (x + y) (x2 + y2 + 2xy - 3xy)
= x (x + y) (x2 + y2 - xy)
Solution 10
x3+ 2x2 + 5x + 10
= x2 (x + 2) + 5 (x + 2)
= (x2 + 5) (x + 2)
Solution 11
x2 + xy - 2xz - 2yz
= x (x + y) - 2z (x + y)
= (x+ y) (x - 2z)
Solution 12
a3b - a2b + 5ab - 5b
= a2b (a - 1) + 5b (a - 1)
= (a - 1) (a2b + 5b)
= (a - 1) b (a2 + 5)
= b (a - 1) (a2 + 5)
Solution 13
8 - 4a - 2a3 + a4
= 4(2 - a) - a3 (2 - a)
= (2 - a) (4 - a3)
Solution 14
x3 - 2x2y + 3xy2 - 6y3
= x2 (x - 2y) + 3y2 (x - 2y)
= (x - 2y) (x2 + 3y2)
Solution 15
px + pq - 5q - 5x
= p(x + q) - 5 (q + x)
= (x + q) (p - 5)
Solution 16
x2 - xy + y - x
= x (x - y) - 1 (x - y)
= (x - y) (x - 1)
Solution 17
(3a - 1)2 - 6a + 2
= (3a - 1)2 - 2 (3a - 1)
= (3a - 1) [(3a - 1) - 2]
= (3a - 1) (3a - 3)
= 3(3a - 1) (a - 1)
Solution 18
(2x - 3)2 - 8x + 12
= (2x - 3)2 - 4 (2x - 3)
= (2x - 3) (2x - 3 - 4)
= (2x - 3) (2x - 7)
Solution 19
a3 + a - 3a2 - 3
= a(a2 + 1) - 3 (a2 + 1)
= (a - 3) (a2 + 1)
Solution 20
3ax - 6ay - 8by + 4bx
= 3a (x - 2y) + 4b (x - 2y)
= (x - 2y) (3a + 4b)
Solution 21
abx2 + a2x + b2x +ab
= ax (bx + a) + b (bx + a)
= (bx + a) (ax + b)
Solution 22
x3 - x2 + ax + x - a - 1
= x3 - x2 + ax - a + x - 1
= x2 (x - 1) + a (x - 1) + 1 (x - 1)
= (x - 1) (x2 + a + 1)
Solution 23
2x + 4y - 8xy - 1
= 2x - 1 - 8xy + 4y
= (2x - 1) - 4y (2x - 1)
= (2x - 1) (1 - 4y)
Solution 24
ab (x2 + y2) - xy (a2 + b2)
= abx2 + aby2 - a2xy - b2xy
= abx2 - a2xy + aby2 - b2xy
= ax (bx - ay) + by(ay - bx)
= (bx - ay) (ax - by)
Solution 25
a2 + ab (b + 1) + b3
= a2 + ab2 + ab + b3
= a2 + ab + ab2 + b3
= a (a + b) + b2 (a + b)
= (a + b) (a + b2)
Solution 26
a3 + ab (1 - 2a) - 2b2
= a3 + ab - 2a2b - 2b2
= a (a2 + b) - 2b (a2 + b)
= (a2 + b) (a - 2b)
Solution 27
2a2 + bc - 2ab - ac
= 2a2 - 2ab - ac + bc
= 2a (a - b) - c (a - b)
= (a - b) (2a - c)
Solution 28
(ax + by)2 + (bx - ay)2
= a2x2 + b2y2 + 2abxy + b2x2 + a2y2 - 2abxy
= a2x2 + b2y2 + b2x2 + a2y2
= a2x2 + b2x2 + b2y2 + a2y2
= x2 (a2 + b2) + y2(a2 + b2)
= (a2 + b2) (x2 + y2)
Solution 29
a (a + b - c) - bc
= a2 + ab - ac - bc
= a(a + b) - c (a + b)
= (a - c) (a + b)
Solution 30
a(a - 2b - c) + 2bc
= a2 - 2ab - ac + 2bc
= a (a - 2b) - c (a - 2b)
= (a - 2b) (a - c)
Solution 31
a2x2 + (ax2 + 1)x + a
= a2x2 + ax3 + x + a
= ax2 (a + x) + 1 (x + a)
= (ax2 + 1) (a + x)
Solution 32
ab (x2 + 1) + x (a2 + b2)
= abx2 + ab + a2x + b2x
= abx2 + a2x + ab + b2x
= ax (bx + a) + b (bx + a)
= (bx + a) (ax + b)
Solution 33
x2 - (a + b) x+ ab
= x2 - ax - bx + ab
= x (x - a) - b(x - a)
= (x - a) (x - b)
Solution 34
![]()