Class 10 R S AGGARWAL AND V AGGARWAL Solutions Maths Chapter 9 - Constructions
Constructions Exercise Ex. 9A
Solution 1

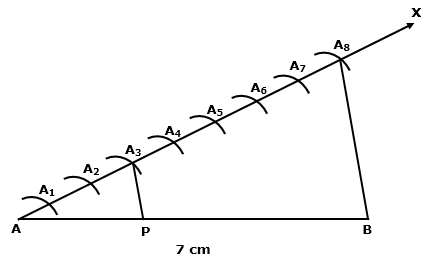
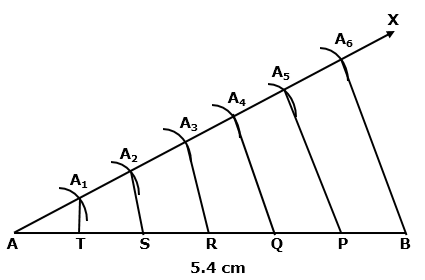
Solution 2(i)
Steps:
1. Draw AB = 8 cm
2. Draw ray AX making an acute angle of 45 degree with AB
3. Draw ray BY making an acute angle of 45 degree with AB
4. Mark four points A1, A2, A3, A4 on AX and five points B1, B2, B3, B4, B5 on BY in such a way that AA1=A1A2 =A2A3=A3A4=BB1=B1B2=B2B3=B3B4=B4B5
5. Now join A4 B5
6. Let this intersect at C, which is the point that divided AB in 4:5 ratio
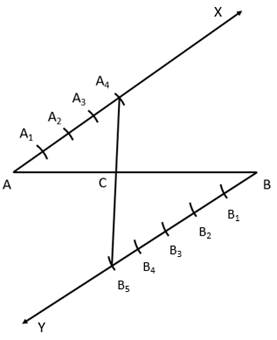
Solution 2(ii)


Solution 3

Solution 4

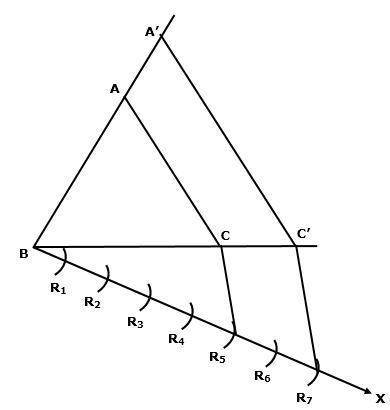
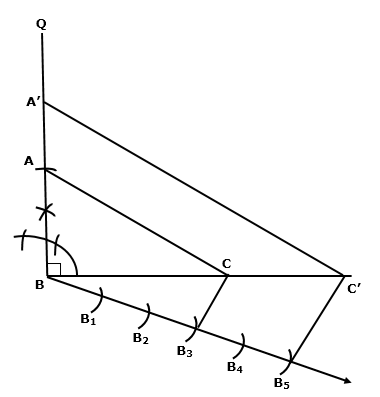
Solution 5
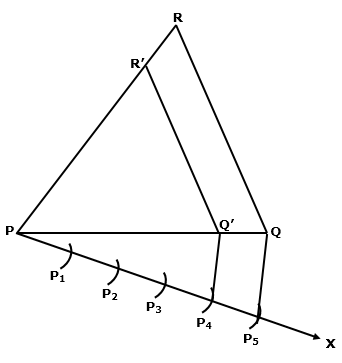
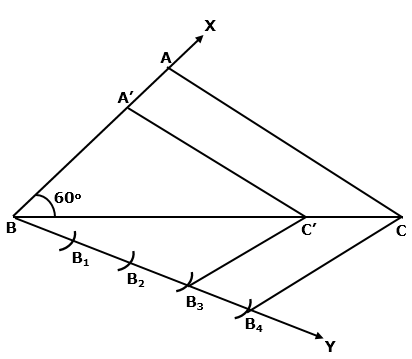
Steps:
1. Construct ΔABC
2. Draw a ray BX making acute angle with BC
3. Mark four points B1, B2, B3, B4 on BY in such a way that BB1=B1B2=B2B3=B3B4
4. Join B4 with C
5. Draw B3C' parallel to B4C
6. Now draw C'A' parallel to AC
7. Hence, ΔA'BC' is the required triangle
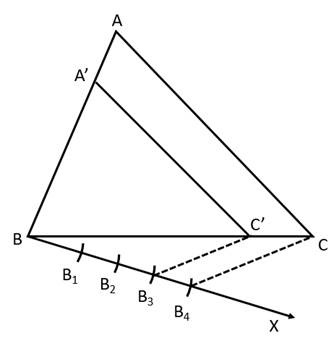
Solution 6

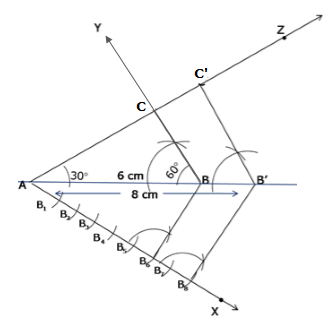
Solution 7

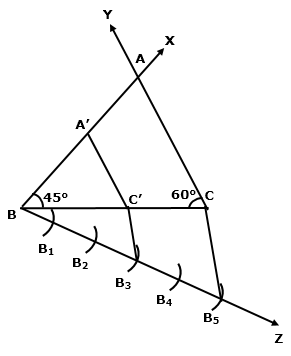
Solution 8
BC will be divided in the ratio 3 : 4
Solution 9


Solution 10

Constructions Exercise Ex. 9B
Solution 1

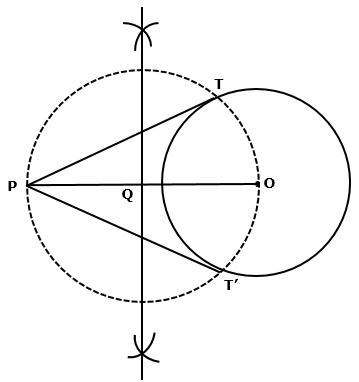
Solution 2

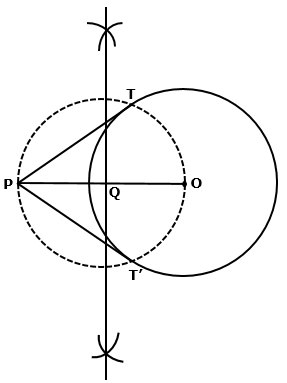
Solution 3
Steps:
1. Draw a circle of 3 cm
2. Draw AB diameter and extend AB on both sides such that OP = OQ = 7cm
3. Now draw perpendicular bisectors of OP and OQ, and let them bisect OP and OQ at S and T respectively
4. Now taking S as center and radius SP, cut arcs on the circle and join the points of intersection with P using straight line
5. Also, taking T as center and radius TQ, cut arcs on the circle and join the points of intersection with Q using straight line
6. Thus we have the required tangents
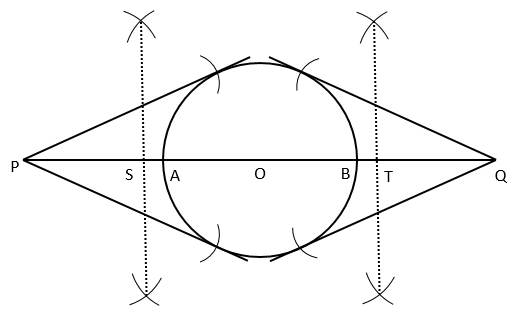
Solution 4

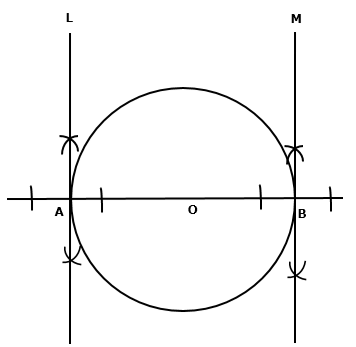
Solution 5


Solution 6

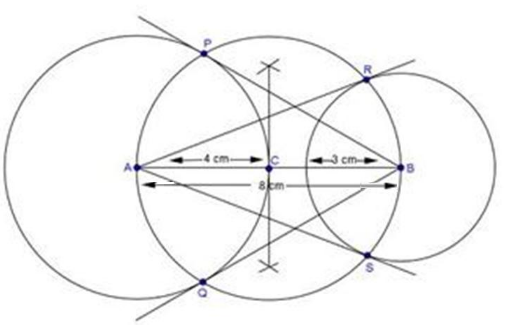
Solution 7

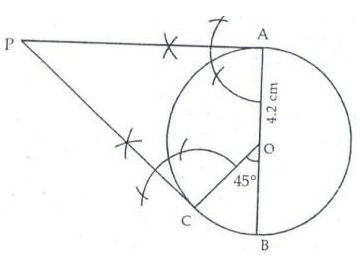
Solution 8

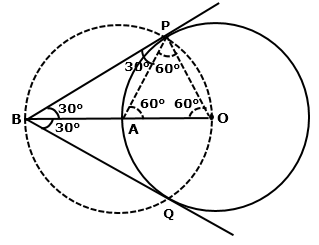
Solution 9

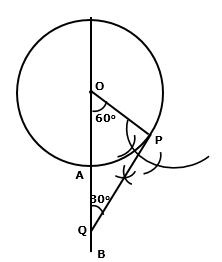
Solution 10

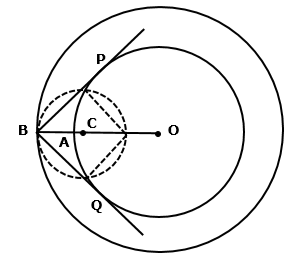
Solution 11
Steps
1. Draw two concentric circles of radii 3 cm and 5 cm with center O
2. Take a point A on circle and join AO
3. Now draw perpendicular bisector of AO, and let it bisect OA at B
4. Now, taking B as center and radius AB, cut arcs on the inner circle and join the points of intersection with A using straight line
5. Thus we have the required tangents
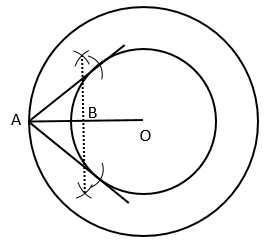
Solution 12
Steps
1. Draw a circle of any radius with center O
2. Take a point A outside the circle and join AO
3. Now draw perpendicular bisector of AO, and let it bisect OA at B
4. Now, taking B as center and radius AB, cut arcs on the circle and join the points of intersection with A using straight line
5. Thus we have the required tangents
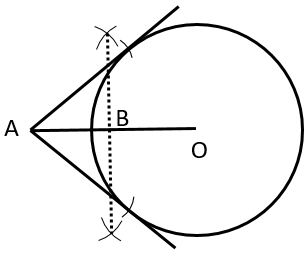
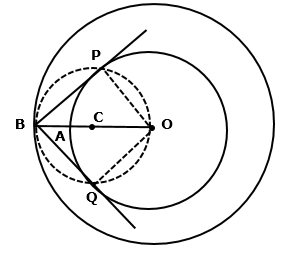
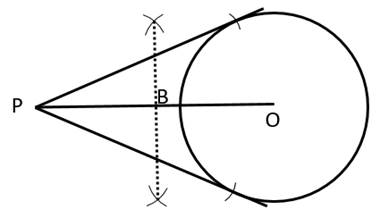
Solution 13
Steps:
1. Draw a circle of radius 3 cm with center O
2. Take a point P outside the circle such that OP = 6.5 cm and join OP
3. Now draw perpendicular bisector of OP, and let it bisect OP at B
4. Now, taking B as center and radius PB, cut arcs on the circle and join the points of intersection with P using straight line
5. Thus we have the required tangents
Constructions Exercise Test Yourself
Solution 1

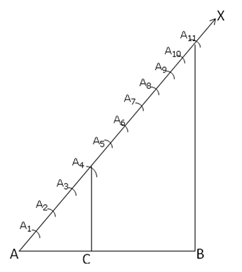
Solution 2

Solution 3

Solution 4

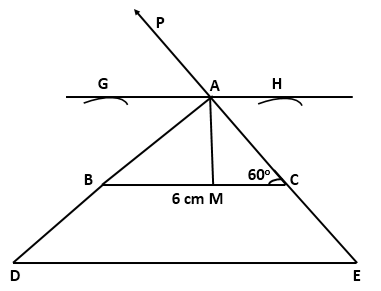
Solution 5

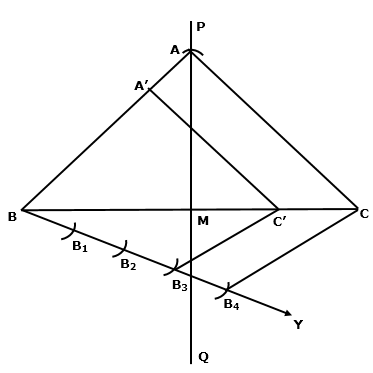
Solution 6


Solution 7

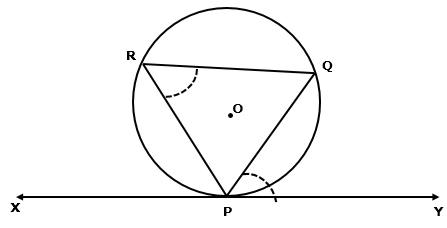
Solution 8

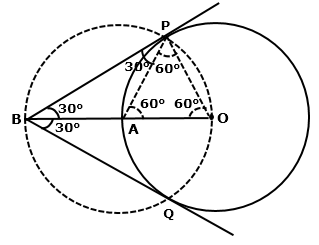
Solution 9

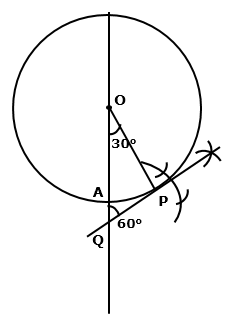
Solution 10