Class 10 R S AGGARWAL AND V AGGARWAL Solutions Maths Chapter 8 - Circles
Circles Exercise Ex. 8A
Solution 1
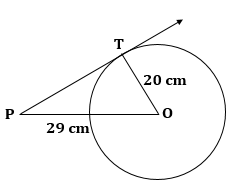
Let O be the centre of the circle and PT be the length of tangent from P to the circle.
Then, OT = 20 cm and OP = 29 cm
Since tangent to a circle is always perpendicular to the radius through the point of contact.
∴ ∠OTP = 90o
In right ΔOTP,
OP2 = OT2 + PT2
⇒ 292 = 202 + PT2
⇒ PT2 = 292 - 202 = (29 - 20)(29 + 20) = 9 × 49 = 441
⇒ PT = 21 cm
Hence, the length of the tangent drawn from P to the circle is 21 cm.
Solution 2
PA is the tangent to the circle with centre O and radius, such that PO = 25 cm, PA = 24 cm
In 
PAO, 
A = 90,
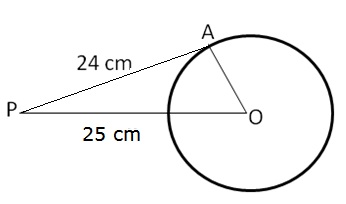
By Pythagoras theorem:
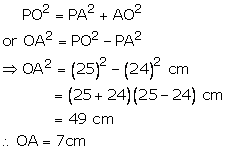
Hence, the radius of the circle is 7 cm.
Solution 3
Solution 4
Solution 5
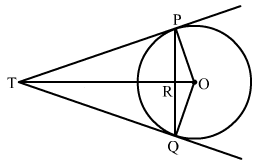
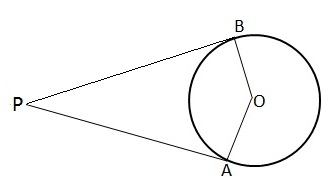
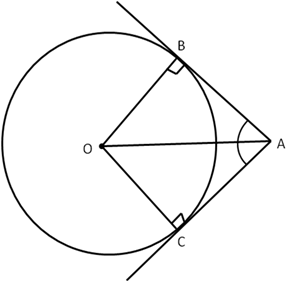
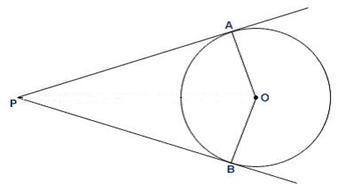
Given AP is a tangent at A and OA is radius through A and PA and PB are the tangent segments to circle with centre O.
Therefore, OA is perpendicular to AP, similarly, OB is perpendicular to BP.
OAP = 90
And OBP = 90
So, OAP = OBP = 90
OBP + OAP = (90 + 90) = 180
Thus, the sum of opposite angles of quad. AOBP is 180
AOBP is a cyclic quadrilateral
Solution 6
Solution 7
Given: From an external point P, tangent PA and PB are drawn to a circle with centre O. CD is the tangent to the circle at a point E and PA = 14cm.
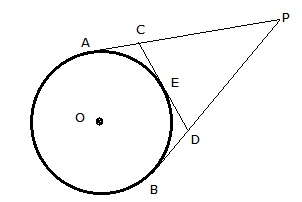
Since the tangents from an external point are equal, we have
PA = PB,
Also, CA = CE and DB = DE
Perimeter of 
PCD = PC + CD + PD
=(PA - CA) + (CE + DE) +(PB - DB)
= (PA - CE) + (CE + DE) + (PB - DE)
= (PA + PB) = 2PA = 2(14) cm
= 28 cm
Hence, the Perimeter of 
PCD = 28 cm
Solution 8
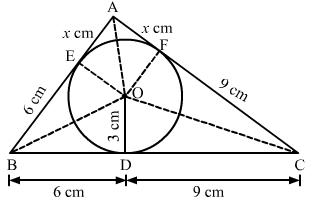
A circle is inscribed in a triangle ABC touching AB, BC and CA at P, Q and R respectively.
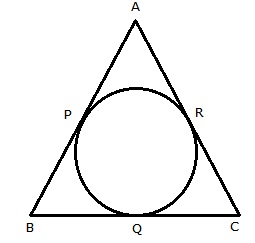
Also, AB = 10 cm, AR = 7cm, CR = 5cm
AR, AP are the tangents to the circle
AP = AR = 7cm
AB = 10 cm
BP = AB - AP = (10 - 7)= 3 cm
Also, BP and BQ are tangents to the circle
BP = BQ = 3 cm
Further, CQ and CR are tangents to the circle
CQ = CR = 5cm
BC = BQ + CQ = (3 + 5) cm = 8 cm
Hence, BC = 8 cm
Solution 9
Let the circle touches the sides AB, BC, CD and DA at P, Q, R, S respectively
We know that the length of tangents drawn from an exterior point to a circle are equal
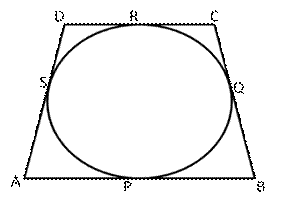
AP = AS ----(1) {tangents from A}
BP = BQ ---(2) {tangents from B}
CR = CQ ---(3) {tangents from C}
DR = DS----(4) {tangents from D}
Adding (1), (2) and (3) we get
AP + BP + CR + DR = AS + BQ + CQ + DS
(AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
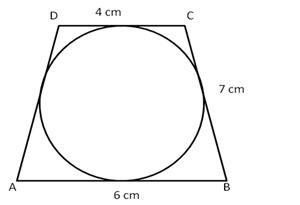
AB + CD = AD + BC
AD = (AB + CD) - BC = {(6 + 4) - 7} cm = 3 cm
Hence, AD = 3 cm
Solution 10
Solution 11
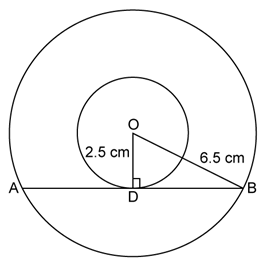
Given O is the centre of two concentric circles of radii 4 cm and 6 cm respectively. PA and PB are tangents to the outer and inner circle respectively. PA = 10cm. Join OA, OB and OP.
Then, OB = 4 cm, OA= 6 cm and PA = 10 cm
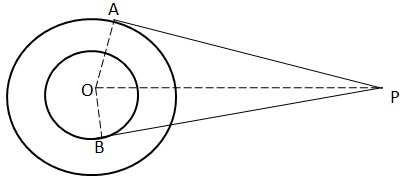
In triangle OAP,
Hence, BP = 10.9 cm
Solution 12
Solution 13
Solution 14
Solution 15
Solution 16
Circles Exercise Ex. 8B
Solution 1
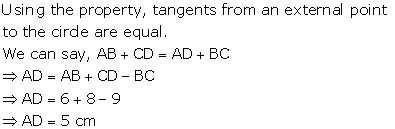
Solution 2
Solution 3
Solution 4
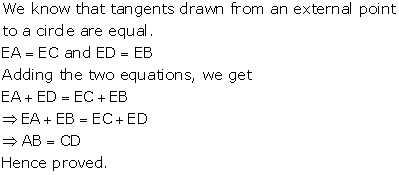
Solution 5
Solution 6
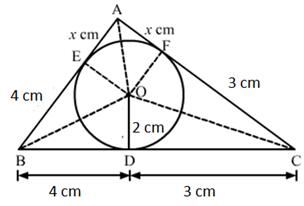
Solution 7
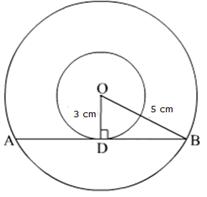
Solution 8
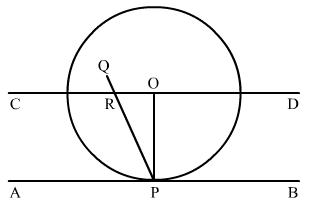
Solution 9
Solution 10
Solution 11
Solution 12
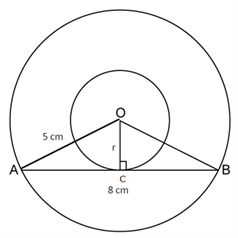
Solution 13
Solution 14
Solution 15
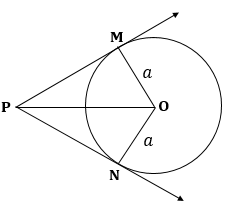
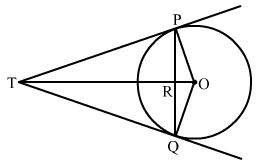
PM and PN are tangents to a circle.
∴ OM ⏊ PM and ON ⏊ PN
⇒ ∠OMP = 90o and ∠ONP = 90o
In ΔOMP and ΔONP,
OM = ON (radii of same circle)
∠OMP = ∠ONP = 90o
OP = OP (common)
∴ ΔOMP ≌ ΔONP (RHS congruency)
∴ ∠OPM = ∠OPN (CACT)
⇒ ∠OPM 
Hence, the length of OP is 
.
Circles Exercise MCQ
Solution 1
Correct option : (b)
We can draw only 2 tangents from an external point to a circle.
Solution 2
Solution 3
Solution 4
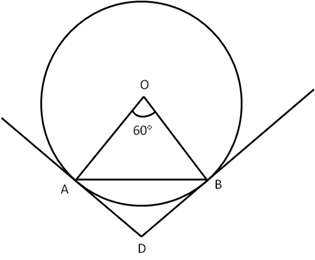
Correct option: (d)
The diameter of the circle always passes through the centre. This means all the diameters of a given circle will intersect at the centre, and hence they cannot be parallel.
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
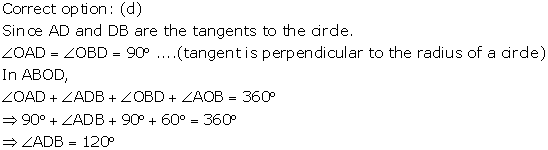
Solution 11
Solution 12
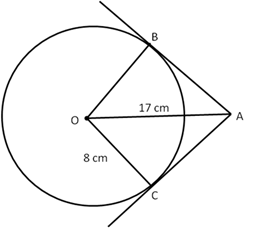
Solution 13
Solution 14
Solution 15
Solution 16
Solution 17
Solution 18
Solution 19
Solution 20
Solution 21
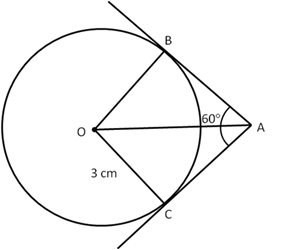
Solution 22
Solution 23
Solution 24
Solution 25
Solution 26
Solution 27
Solution 28
Solution 29
Solution 30
Solution 31
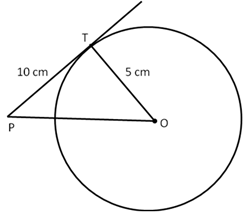
Solution 32
Solution 33
Solution 34
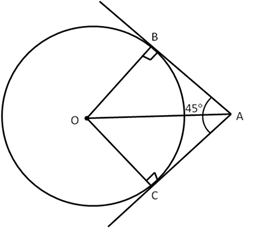
Solution 35
Solution 36
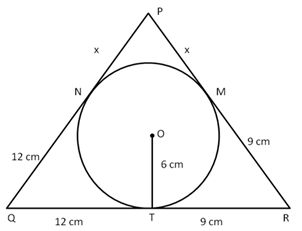
Solution 37
Solution 38
Solution 39
Solution 40
Solution 41
Solution 42
Solution 43
Solution 44
Solution 45
Solution 46
Solution 47
Solution 48
Solution 49
Solution 50
Correct option: (d)
Options (a), (b) and (c) are all true.
However, option (d) is false since we can draw only parallel tangents on either side of the diameter, which would be parallel to a given line.
Solution 51
Correct option: (d)
Options (a), (b) and (c) are all true.
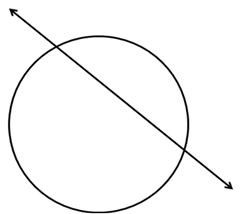
However, option (d) is false since a straight line can meet a circle at two points even as shown below.
Solution 52
Correct option: (d)
Options (a), (b) and (c) are true.
However, option (d) is false since it is not possible to draw a tangent from a point inside a circle.
Solution 53
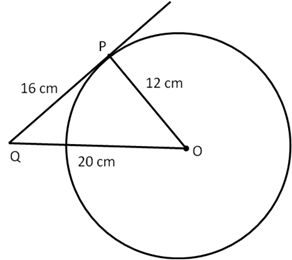
Solution 54
Solution 55
Circles Exercise Test Yourself
Solution 1
Solution 2
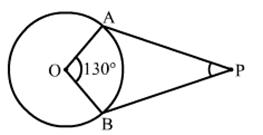
Solution 3
Solution 4
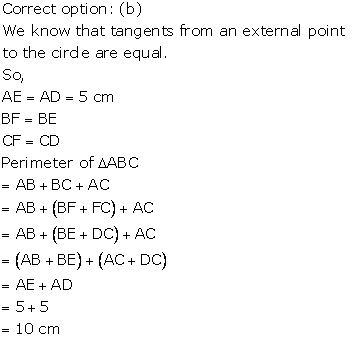
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
- A line intersecting a circle in two distinct points is called a secant.
- A circle can have two parallel tangents at the most.
- The common point of a tangent to a circle and the circle is called the point of contact.
- A circle can have infinitely many tangents.
Solution 10
Solution 11
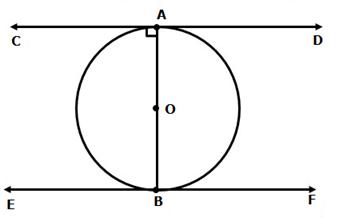
Solution 12
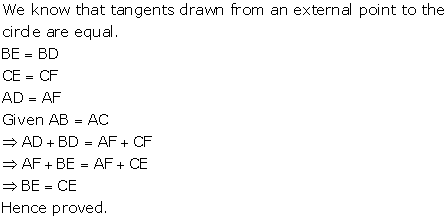
Solution 13
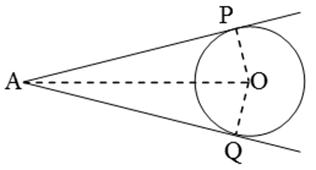
Solution 14
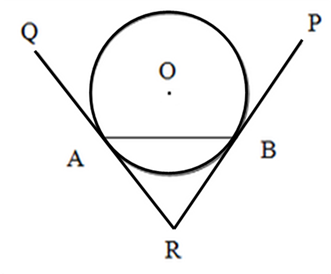
Solution 15
Solution 16
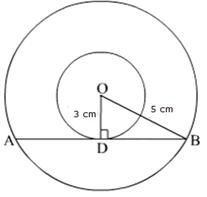
Solution 17
Solution 18
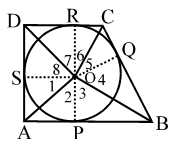
Solution 19
Solution 20
