Class 10 R S AGGARWAL AND V AGGARWAL Solutions Maths Chapter 12 - Trigonometric Ratios of Complementary Angles
Trigonometric Ratios of Complementary Angles Exercise Ex. 12
Solution 1(i)
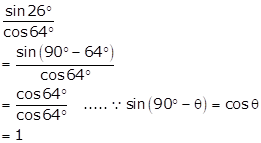
Solution 1(ii)
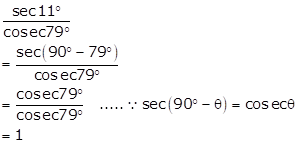
Solution 1(iii)
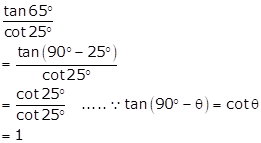
Solution 1(iv)
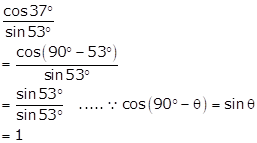
Solution 1(v)
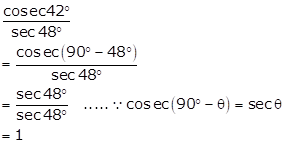
Solution 1(vi)
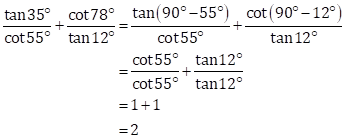
Solution 2(i)
L.H.S = cos81˚ - sin9˚
= cos(90˚- 9˚) - sin9˚
= sin9˚ - sin9˚ ….. ∵ cos(90˚- θ) = sin θ
= 0
= R.H.S
Hence proved.
Solution 2(ii)
L.H.S = tan71˚ - cot19˚
= tan(90˚- 19˚) - cot19˚
= cot19˚ - cot19˚ ….. ∵ tan(90˚- θ) = cot θ
= 0
= R.H.S
Hence proved.
Solution 2(iii)
L.H.S = cosec60˚ - sec30˚
= cosec(90˚- 30˚) - sec30˚
= sec30˚ - sec30˚ ….. ∵ cosec(90˚- θ) = sec θ
= 0
= R.H.S
Hence proved.
Solution 2(iv)
L.H.S = cot34˚ - tan56˚
= cot(90˚- 56˚) - tan56˚
= tan56˚ - tan56˚ ….. ∵ cot(90˚- θ) = tan θ
= 0
= R.H.S
Hence proved.
Solution 2(v)
L.H.S = sin2 48˚ + sin2 42˚
= sin2 (90˚- 42˚) + sin2 42˚
= cos2 42˚ + sin2 42˚ ….. ∵ sin(90˚- θ) = cos θ
= 1 ….. ∵ sin2 θ+ cos2θ= 1
= R.H.S
Hence proved.
Solution 2(vi)
L.H.S = cos2 72˚ + cos2 18˚
= cos2 (90˚- 18˚) + cos2 18˚
= sin2 18˚ + cos2 18˚ ….. ∵ cos(90˚- θ) = sin θ
= 1 ….. ∵ sin2 θ+ cos2θ= 1
= R.H.S
Hence proved.
Solution 3(i)
L.H.S = sin2 12˚ + sin2 78˚
= sin2 (90˚- 78˚) + sin2 78˚
= cos2 78˚ + sin2 78˚ ….. ∵ sin(90˚- θ) = cos θ
= 1 ….. ∵ sin2 θ+ cos2θ= 1
= R.H.S
Hence proved.
Solution 3(ii)
L.H.S = sec2 29˚- cot2 61˚
= sec2 29˚ - cot2 (90˚- 29˚)
= sec2 29˚ - tan229˚ ….. ∵ cot(90˚- θ) = tan θ
= 1 ….. ∵ sec2 θ - tan2θ= 1
= R.H.S
Hence proved.
Solution 3(iii)
L.H.S = tan2 56˚- cot2 34˚
= tan2 56˚- cot2 (90˚- 56˚)
= tan2 56˚- tan2 56˚ ….. ∵ cot(90˚- θ) = tan θ
= 0
= R.H.S
Solution 3(iv)
L.H.S = cos2 57˚ - sin2 33˚
= cos2 57˚ - sin2(90˚- 57˚)
= cos2 57˚ - cos2 57˚ ….. ∵ sin(90˚- θ) = cos θ
= 0
= R.H.S
Hence proved.
Solution 3(v)
L.H.S = sec2 50˚- cot2 40˚
= sec2 50˚ - cot2 (90˚- 50˚)
= sec2 50˚ - tan250˚ ….. ∵ cot(90˚- θ) = tan θ
= 1 ….. ∵ sec2 θ - tan2θ= 1
= R.H.S
Hence proved.
Solution 3(vi)
L.H.S = cosec2 72˚ - tan2 18˚
= cosec2 72˚ - tan2 (90˚- 72˚)
= cosec2 72˚ - cot2 72˚ ….. ∵ tan(90˚- θ) = cot θ
= 1 ….. ∵ cosec2 θ - cot2θ= 1
= R.H.S
Hence proved.
Solution 4(i)
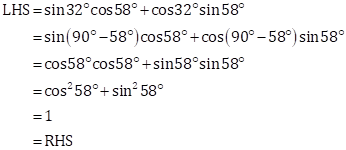
Solution 4(ii)

Solution 4(iii)
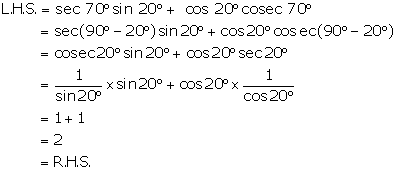
Solution 4(iv)
L.H.S = tan15˚ tan60˚ tan75˚
= (tan15˚ tan75˚) tan60˚
= [tan 15˚tan(90˚- 15˚)] tan60˚
= (tan 15˚cot 15˚) tan60˚ ……∵ tan(90˚- θ) = cot θ
= (tan 15˚×1/tan15˚) tan60˚ …… ∵ cot θ = 1/tan θ
= 1 × √3
= √3
= R.H.S
Hence proved.
Solution 4(v)
L.H.S = tan48˚ tan23˚ tan42˚ tan67˚ tan45˚
= (tan48˚ tan42˚) (tan23˚ tan67˚) tan45˚
= [tan 48˚tan(90˚- 48˚)] [tan 23˚tan(90˚- 23˚)] tan45˚
= (tan 48˚cot 48˚) (tan 23˚cot 23˚) tan45˚
……∵ tan(90˚- θ) = cot θ
= (tan 48˚×1/tan 48˚) (tan 23˚×1/tan 23˚) tan45˚
…… ∵ cot θ = 1/tan θ
= 1×1×1
= 1
= R.H.S
Hence proved.
Solution 4(vi)
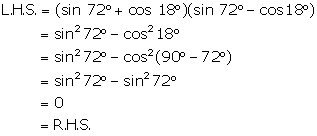
Solution 4(vii)
L.H.S = cosec 39˚cos51˚ + tan21˚ cot 69˚- sec2 21˚
= cosec 39˚cos(90˚- 39˚) + tan 21˚cot(90˚- 21˚) - sec2 21˚
= cosec 39˚sin 39˚+ tan 21˚tan 21˚- sec2 21˚
….. ∵ cot(90˚- θ) = tan θ and cos(90˚- θ) = sin θ
= 1 + tan221˚- sec2 21˚
= 1 - (sec2 21˚- tan221˚)
= 1 - 1 ……. ∵ sec2 θ - tan2θ = 1
= 0
= R.H.S
Hence proved.
Solution 5(i)
sin 72˚ + cosec 72˚
= sin(90˚- 18˚) + cosec(90˚- 18˚)
= cos 18˚+ sec 18˚
Solution 5(ii)
cosec 66˚ + tan 66˚
= cosec(90˚- 24˚) + tan(90˚- 24˚)
= sec 24˚+ cot 24˚
Solution 5(iii)
tan 68˚ + sec 68˚
= tan(90˚- 22˚) + sec(90˚- 22˚)
= cot 22˚+ cosec 22˚
Solution 5(iv)
cot 59˚ + cosec 59˚
= cot(90˚- 31˚) + cosec(90˚- 31˚)
= tan 31˚+ sec 31˚
Solution 5(v)
cos 51˚ + cot 49˚ - sec 47˚
= cos(90˚- 39˚) + cot(90˚- 41˚) - sec(90˚- 43˚)
= sin 39˚+ tan 41˚- cosec 43˚
Solution 5(vi)
sin 67˚ + cos 75˚
= sin(90˚- 23˚) + cos(90˚- 15˚)
= cos 23˚+ sin 15˚
Solution 6
sin 3A = cos (A - 10˚)
⇒ cos(90˚- 3A) = cos (A - 10˚) = ….. ∵ cos(90˚ - θ) = sin θ
∴ 90˚- 3A = A - 10˚
⇒ 4A = 100˚
⇒ A = 25˚
Solution 7
tan A = cot (A + 10˚)
⇒ cot(90˚- A) = cot(A + 10˚) = ….. ∵ cot(90˚ - θ) = tan θ
∴ 90˚- A = A + 10˚
⇒ 2A = 80˚
⇒ A = 40˚
Solution 8
cos 2A = sin (A - 15˚)
⇒ sin(90˚- 2A) = sin (A - 15˚) = ….. ∵ sin(90˚ - θ) = cos θ
∴ 90˚- 2A = A - 15˚
⇒ 3A = 105˚
⇒ A = 35˚
Solution 9
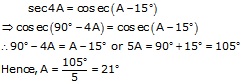
Solution 10
tan 2θ = cot (θ + 6˚)
⇒ cot (θ + 6˚) = cot(90˚- 2θ) ….. ∵ cot(90˚- θ) = tan θ
∴ θ + 6˚= 90˚- 2θ
⇒ 3θ = 84˚
⇒ θ = 28˚
Solution 11
sin (θ + 36˚) = cos θ
⇒ sin (θ + 36˚) = sin(90˚- θ) ….. ∵ sin(90˚ - θ) = cos θ
∴ θ + 36˚= 90˚- θ
⇒ 2θ = 54˚
⇒ θ = 27˚
Solution 12
3 cot 31˚tan 15˚cot 27˚tan 75˚cot 63˚cot 59˚
= 3 (cot 31˚cot 59˚)(tan 15˚tan 75˚)(cot 27˚cot 63˚)
= 3 [cot 31˚cot (90˚- 31˚)] [tan 15˚tan (90˚- 15˚)] [cot 27˚cot (90˚- 27˚)]
= 3 (cot 31˚tan 31˚)(tan 15˚cot 15˚)(cot 27˚tan 27˚)
….. ∵ tan(90˚- θ) = cot θ and cot(90˚- θ) = tan θ
= 3 …..∵ tan θ = 1/ cot θ and cot θ = 1/ tan θ
Solution 13
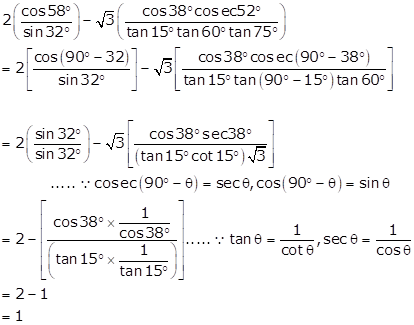
Solution 14
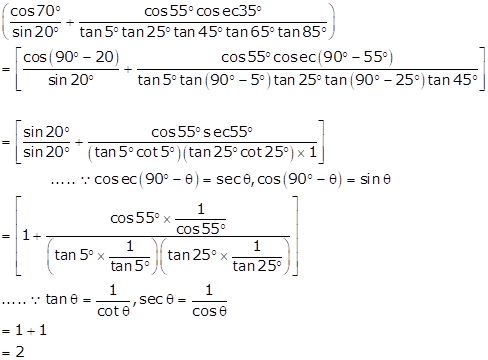
Solution 15
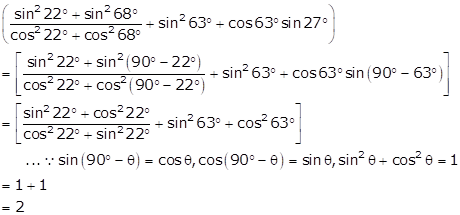
Solution 16
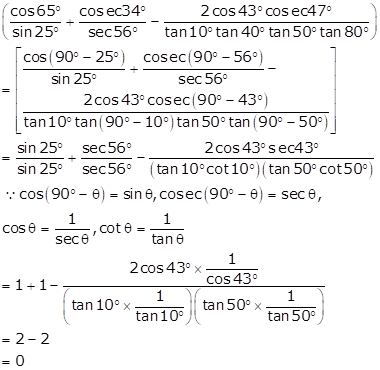
Solution 17
cot θ tan(90˚- θ) - sec(90˚- θ) cosec θ + sin2 65˚+ sin2 25˚+ √3 tan 5˚ tan 45˚ tan 85˚
= cot θ cot θ - cosec θ cosec θ + sin2 (90˚- 25˚)+ sin2 25˚+ √3 (tan 5˚ tan 85˚) tan 45˚
= (cot2θ - cosec2θ) + (cos2 25˚+ sin2 25˚) + √3 [tan 5˚ tan (90˚- 5˚) × 1
= - 1 + 1 + √3 (tan 5˚cot 5˚)
= 0 + √3
(tan 5˚× ![]() )
)
= √3
Solution 18

Solution 19
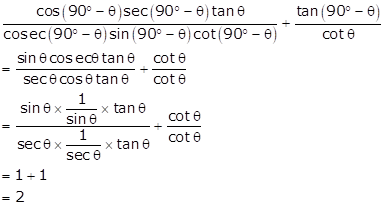
Solution 20
sin(50˚+ θ) - cos(40˚- θ) + tan1˚tan10˚tan20˚tan70˚tan80˚ tan89˚
= cos [90˚- (50˚- θ)] - cos(40˚- θ) + (tan1˚tan89˚) (tan10˚tan80˚) (tan20˚tan70˚) ….. ∵ sin θ = cos(90˚- θ)
= cos(40˚- θ)] - cos(40˚- θ) + [tan1˚tan(90˚- 1˚)] [tan10˚tan(90˚- 10˚)] [tan20˚tan(90˚- 20˚)]
= 0 + (tan1˚cot1˚)( tan10˚cot10˚)( tan20˚cot20˚) … ∵ tan(90˚- θ)= cot θ
= 1 × 1 × 1 …….∵
tan θ = ![]()
= 1
Solution 21
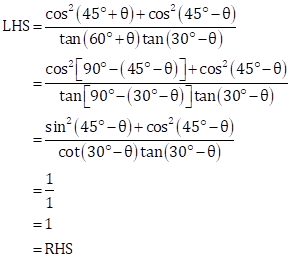
Trigonometric Ratios of Complementary Angles Exercise MCQ
Solution 1
Correct Option: (d)

Solution 2
Correct Option: (c)
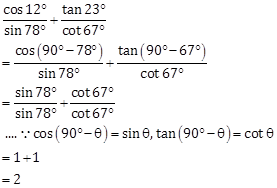
Solution 3
Correct Option: (b)
tan 10˚ tan 15˚ tan 75˚ tan 80˚
= tan 10˚ tan (90˚- 10˚) tan 15˚ tan (90˚- 15˚)
= (tan 10˚ cot 10˚)( tan 15˚ cot 15˚) ……∵ tan (90˚- θ) = cot θ
= (tan 10˚ × 1/tan 10˚)( tan 15˚× 1/tan 15˚) …∵ cot θ = 1/ tan θ
= 1
Solution 4
Correct Option: (c)
tan 5˚ tan 25˚ tan 30˚ tan 65˚ tan 85˚
= tan 5˚tan(90˚- 5˚) tan 25˚ tan(90˚- 25˚) tan 30˚
= (tan 5˚cot 5˚)( tan 25˚cot25˚) tan 30˚… ∵ tan (90˚- θ) = cot θ
= (tan 5˚× 1/tan 5˚)( tan 25˚× 1/tan 25˚) × ![]()
…… ∵ cot θ = 1/ tan θ
= ![]()
Solution 5
Correct Option: (a)
cos 1˚ cos 2˚ cos 3˚ …… cos 180˚
= cos 1˚ cos 2˚ cos 3˚ …… cos 90˚ ….. cos 180˚
= 0 ….. ∵ cos 90˚= 0
Solution 6
Correct Option: (b)
sin 43˚ cos 47˚ + cos 43˚ sin 47˚
= sin 43˚ cos(90˚ - 43˚) + cos 43˚ sin(90˚ - 43˚)
= sin 43˚ sin 43˚+ cos 43˚ cos 43˚ … ∵ cos(90˚- θ) = sin θ
= sin2 43˚+ cos2 43˚ …… ∵ sin2 θ + cos2 θ = 1
= 1
Solution 7
Correct Option: (c)
sec 70˚ sin 20˚ + cos 20˚ cosec 70˚
= sec (90˚- 20˚) sin 20˚ + cos 20˚ cosec (90˚- 20)
= cosec 20˚sin 20˚ + cos 20˚sec 20˚
…. ∵ sec (90˚- θ) = cosec θ, cosec (90˚- θ) = sec θ
= cosec 20˚× 1/cosec 20˚ + cos 20˚× 1/cos 20˚
…. ∵ sin θ = 1/ cosec θ, sec θ = 1/ cos θ
= 1 + 1
= 2
Solution 8
Correct Option: (a)
cosec2 57˚- tan2 33˚
= cosec2 57˚ - tan2 (90˚ - 57˚)
= cosec2 57˚ - cot2 57˚
= 1 …. ∵ cosec2 θ - cot2 θ = 1
Solution 9
Correct Option: (b)
sec2 10˚- cot2 80˚
= sec2 10˚ - cot2 (90˚ - 10˚)
= sec2 10˚ - tan2 10˚
= 1 …. ∵ sec2 θ - tan2 θ = 1
Solution 10
Correct Option: (d)
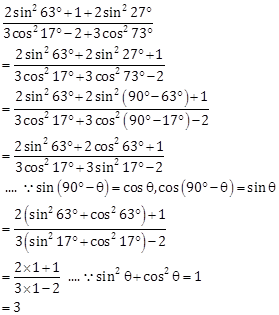
Solution 11
Correct Option: (a)
sin 38˚ - cos 52˚
= sin 38˚ - cos (90˚ - 38˚)
= sin 38˚- sin 38˚ …. ∵ cos (90˚ - θ) = sin θ
= 0
Solution 12
Correct Option: (b)
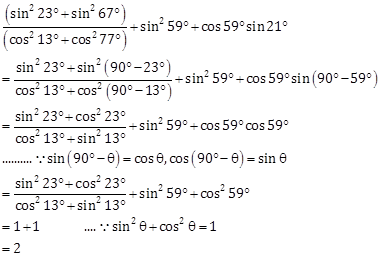
Solution 13
Correct Option: (c)
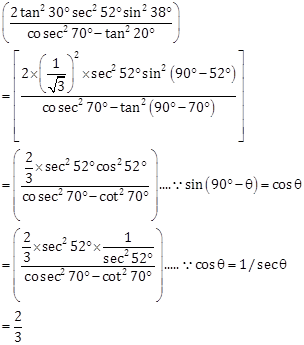
Solution 14
Correct Option: (b)
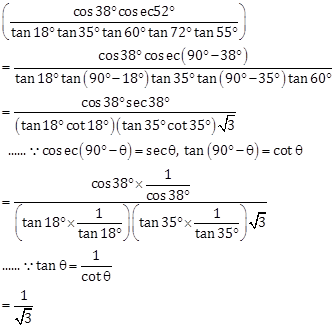
Solution 15
Correct Option: (c)
sin (60˚ + θ) - cos (30˚- θ)
= cos [90˚ - (60˚ + θ)] - cos (30˚- θ) …..∵ sin (90˚ + θ) = cos θ
= cos (30˚- θ) - cos (30˚- θ)
= 0
Solution 16
Correct Option: (d)
sin A = cos B
⇒ sin A = sin (90˚- B)
∴ A = 90˚- B ⇒ A + B = 90˚
Solution 17
Correct Option: (b)
cos (α + β) = 0
⇒ cos (α + β) = cos 90˚
∴ α + β = 90˚ ⇒ α = 90˚- β
∴ α - β = 90˚- β - β = 90˚- 2β
⇒ sin (α - β) = sin (90˚- 2β) = cos 2β … ∵ cos (90˚- θ) = sin θ
Solution 18
Correct Option: (a)
sin (45˚+ θ) - cos (45˚- θ)
= cos [90˚ - (45˚+ θ)] - cos (45˚- θ)
= cos (45˚- θ) - cos (45˚- θ) …. ∵ cos (90˚- θ) = sin θ
= 0
Solution 19
Correct Option: (a)
sec 4A = cosec (A - 10˚)
⇒ cosec (90˚ - 4A) = cosec (A - 10˚) ….∵ cosec (90˚ - θ) = sec θ
∴ 90˚ - 4A = A - 10˚
⇒ 5A = 100˚
⇒ A = 20˚
Solution 20
Correct Option: (c)
sin 3A = cos (A - 10˚)
⇒ cos (90˚ - 3A) = cos (A - 10˚) …. ∵ cos (90˚ - θ) = sin θ
∴ 90˚ - 3A = A - 10˚
⇒ 4A = 100˚
⇒ A = 25˚
Solution 21(i)
cot 34˚- tan 56˚
= cot (90˚- 56˚) - tan 56˚
= tan 56˚- tan 56˚ …. ∵ cot (90˚- θ) = tan θ
= 0
∴ cot 34˚- tan 56˚ = 0
Solution 21(ii)
cosec 31˚- sec 59˚
= cosec (90˚- 59˚) - sec 59˚
= sec 59˚- sec 59˚ …. ∵ cosec (90˚- θ) = sec θ
= 0
∴ cosec 31˚- sec 59˚ = 0
Solution 21(iii)
cos2 67˚+ cos2 23˚
= cos2 (90˚- 23˚) + cos2 23˚
= sin2 23˚ + cos2 23˚
= 1 ….. ∵ sin2 θ + cos2 θ = 1
∴ cos2 67˚+ cos2 23˚ = 1
Solution 21(iv)
cosec2 54˚- tan2 36˚
= cosec2 (90˚- 23˚) - tan2 36˚
= sin2 23˚ + cos2 23˚ …. ∵ cosec (90˚- θ) = sin θ
= 1 ….. ∵ sin2 θ + cos2 θ = 1
∴ cosec2 54˚- tan2 36˚ = 1
Solution 21(v)
sec2 40˚- cot2 50˚
= sec2 (90˚- 50˚) - cot2 50˚
= cosec2 50˚ - cot2 50˚
= 1 …. ∵ cosec2 50˚ - cot2 50˚ = 1
∴ sec2 40˚- cot2 50˚ = 1

