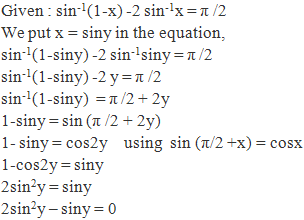Class 12-science NCERT Solutions Maths Chapter 2 - Inverse Trigonometric Functions
Inverse Trigonometric Functions Exercise Ex. 2.1
Solution 1
Solution 2
Solution 3
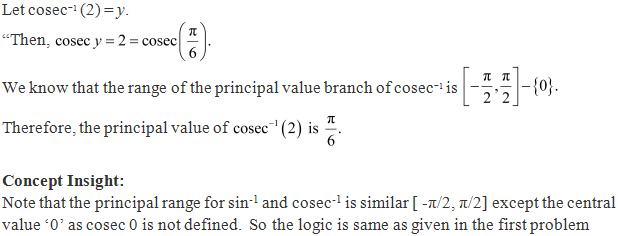
Solution 4
Solution 5
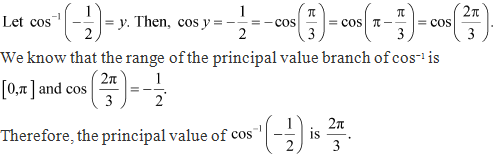
Solution 6
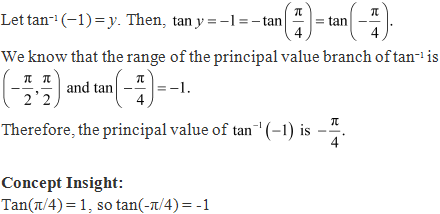
Solution 7
We know that the range of the principal value of sec-1 is
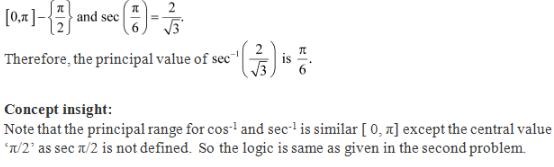
Solution 8
Solution 9
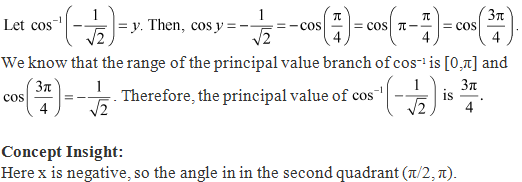
Solution 10
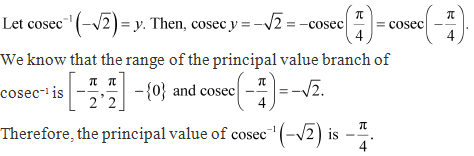
Solution 11
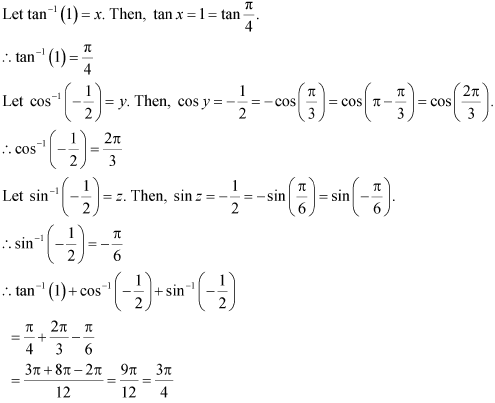
Solution 12
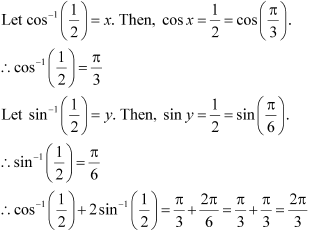
Solution 13
Solution 14
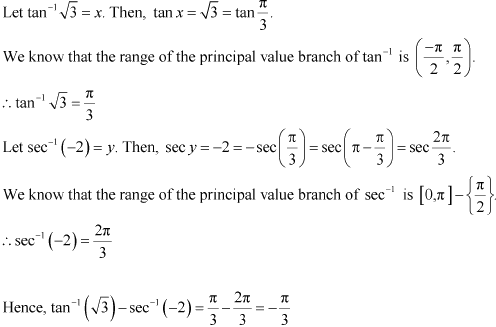
Inverse Trigonometric Functions Exercise Ex. 2.2
Solution 1
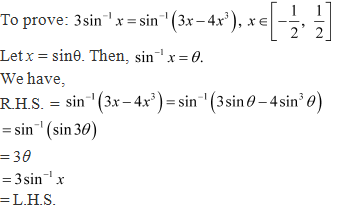
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
Solution 7
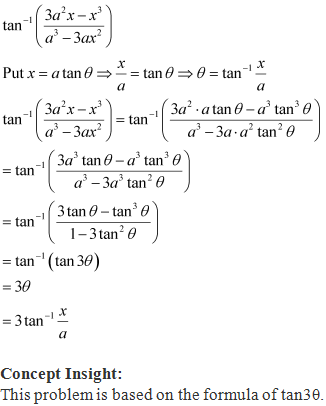
Solution 8
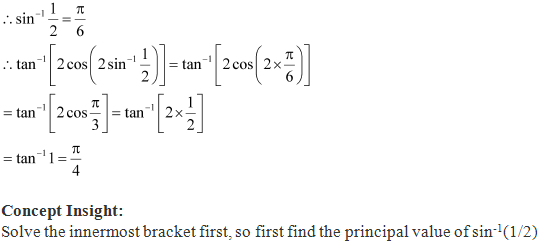
Solution 9
Solution 10
Solution 11
Solution 12
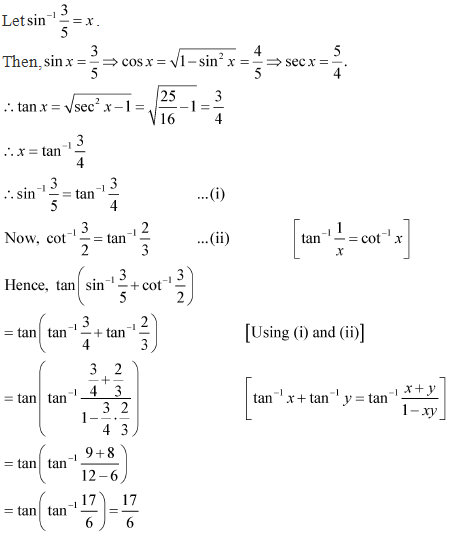
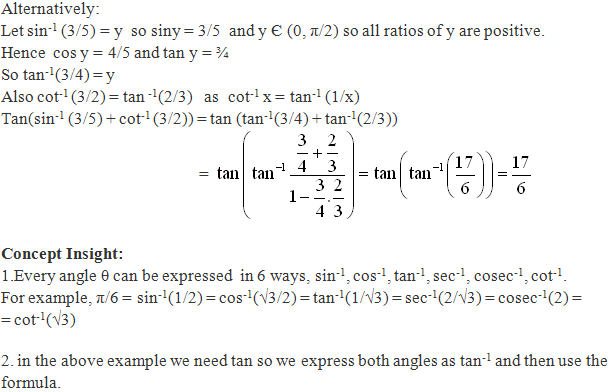
Solution 13
Solution 14
sin (sin-1 (1/5) + cos-1x) = 1
∴ sin-1 (1/5) + cos-1 x = sin-1 1
sin-1 (1/5) + cos-1 x = π/2
sin-1 (1/5) = π/2 - cos-1 x
sin-1 (1/5) = sin-1 x
∴ x = 1/5
We use the results: sin-1 1 = π/2 and sin-1 x + cos-1 x = π/2
Concept Insight:
As R.H.S is ‘1’, it is easier to take sin-1 1 = π/2
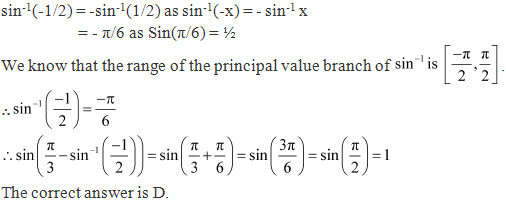
Solution 15
Solution 16
Solution 17
Solution 18
Solution 19
Solution 20
Solution 21
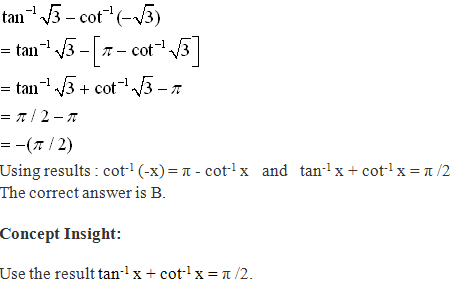
Inverse Trigonometric Functions Exercise Misc. Ex.
Solution 1
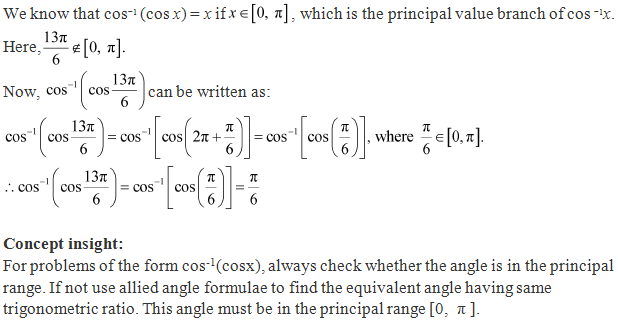
Solution 2
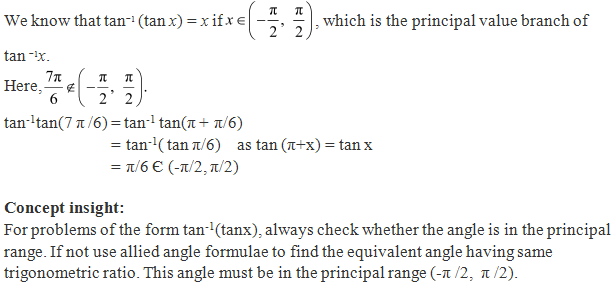
Solution 3
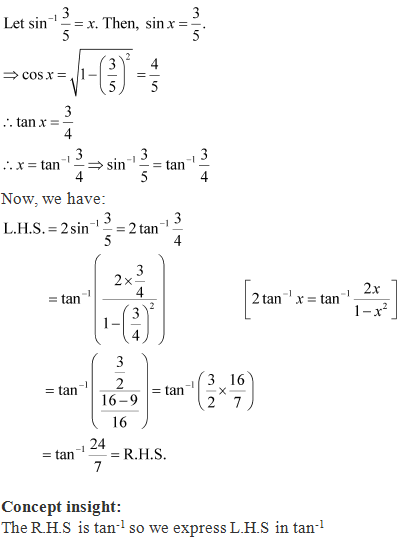
Solution 4
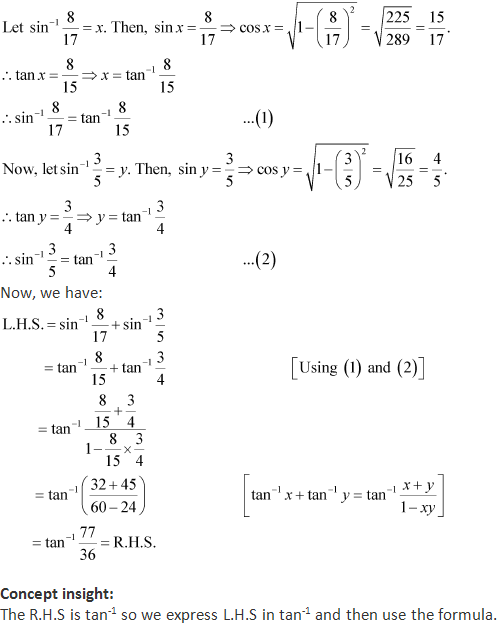
Solution 5
= 
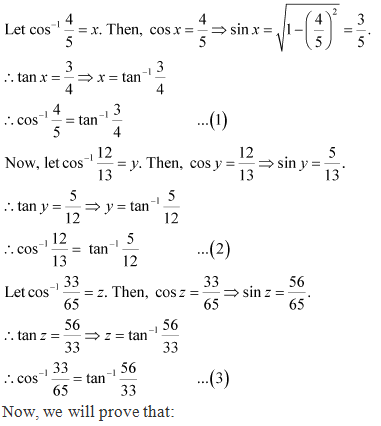
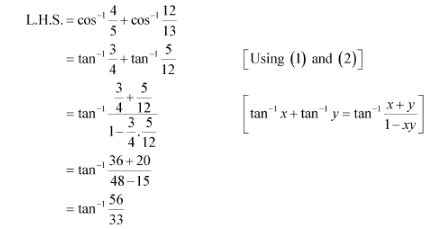
by (3)
= RHS
Solution 6
Let sin-1(3/5) = A and cos-1 (12/13) = B
So sin A = 3/5 and cos B = 12/13
Hence cos A = 4/5 and sin B = 5/13
As R.H.S is sin-1 we use sin (A + B)
Sin (A + B) = sin A cos B + cos A sin B = (3/5) (12/13) + (4/5) (5/13)
= 36/65 + 20/65 = 56/65
Thus A + B = sin-1 (56/65) hence proved.
Concept insight:
If R.H.S is cos-1 or sin-1 then use Cos (A + B) or sin (A + B) as the case may be.
Solution 7
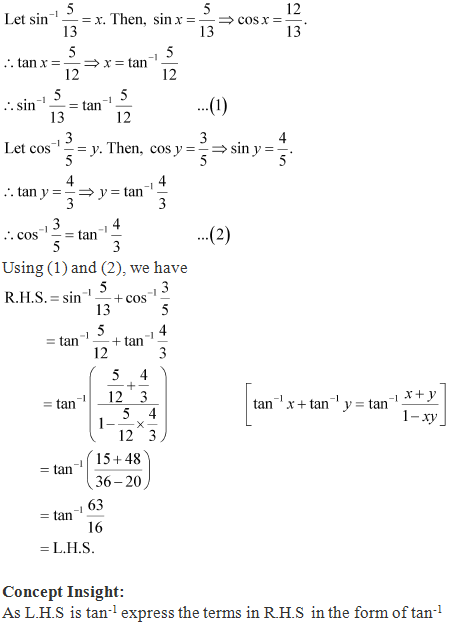
Solution 8
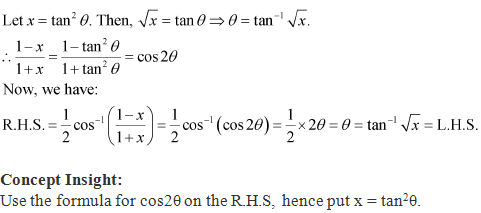
Solution 9
Solution 10
Solution 11
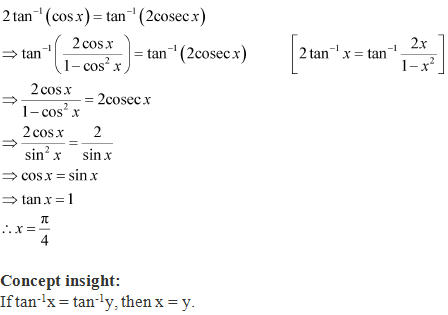
Solution 12
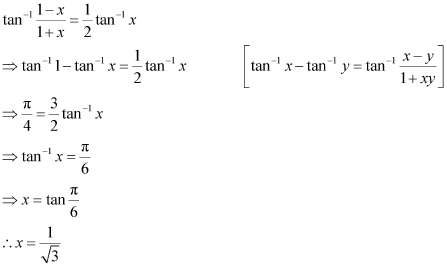
Solution 13
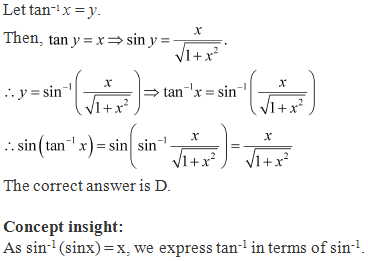
Solution 14
Solution 15
Solution 16
Solution 17
Get in Touch
