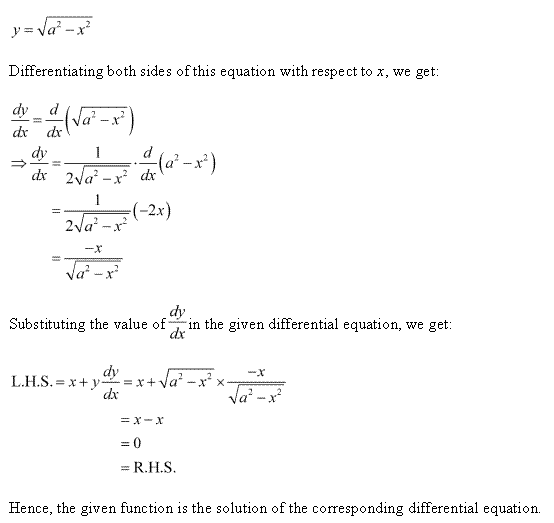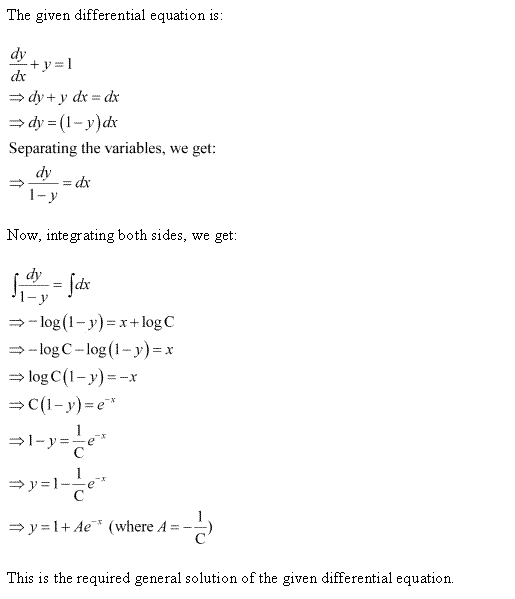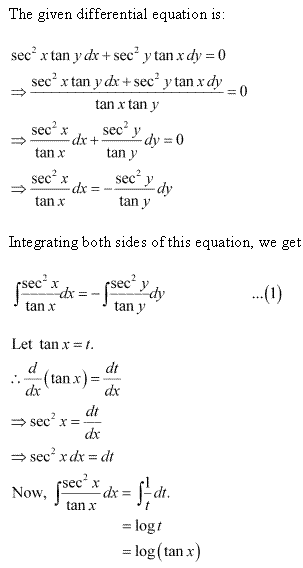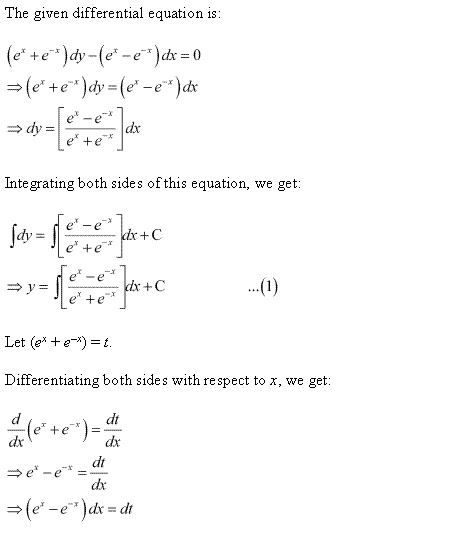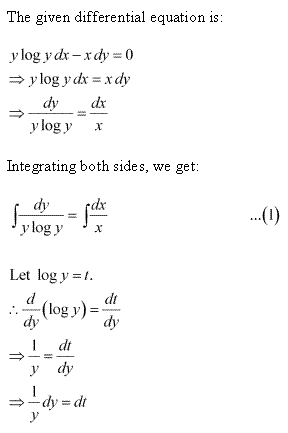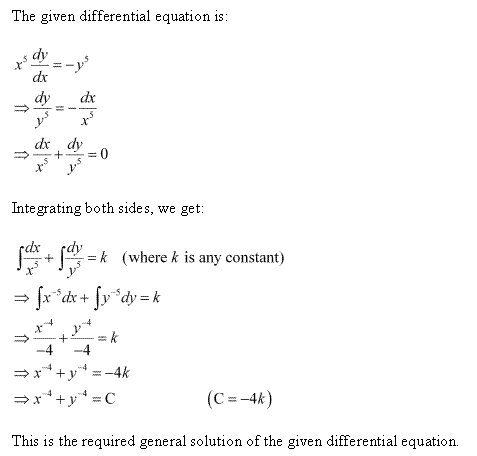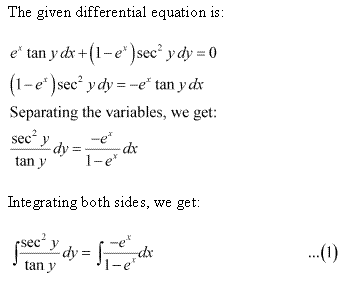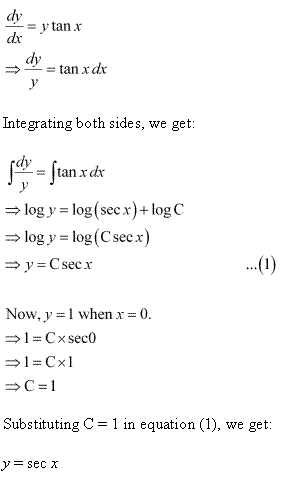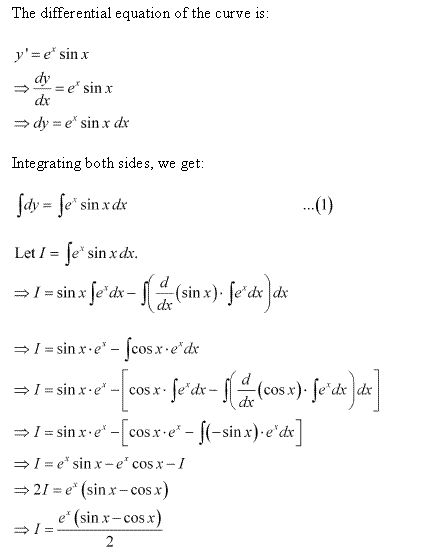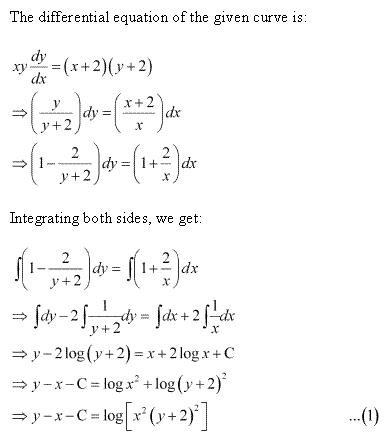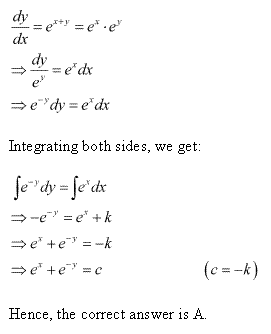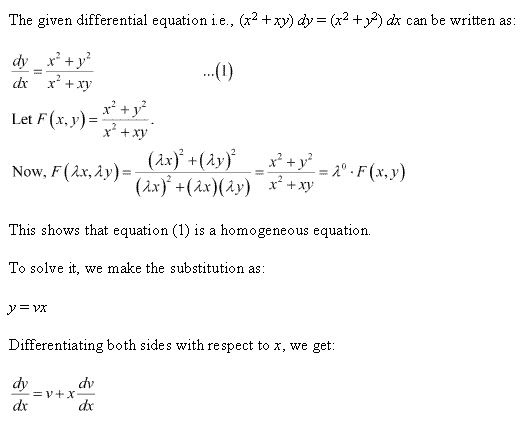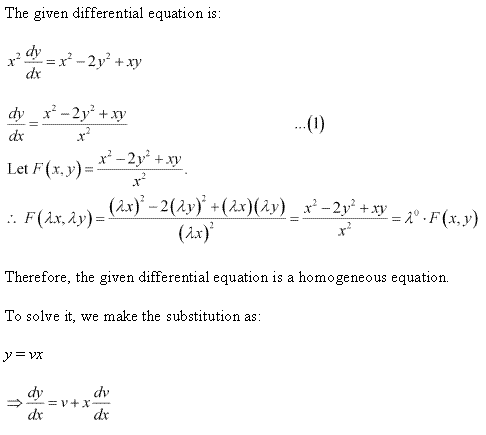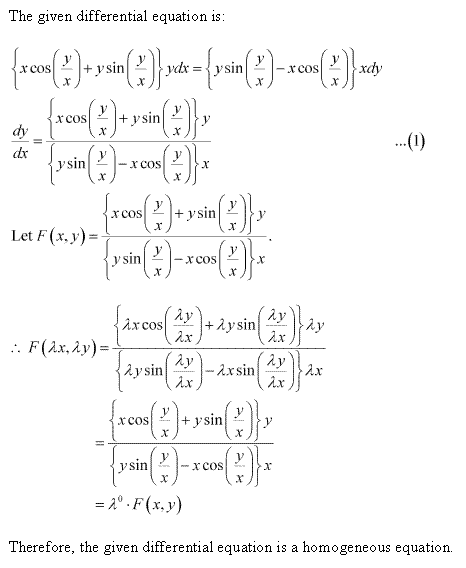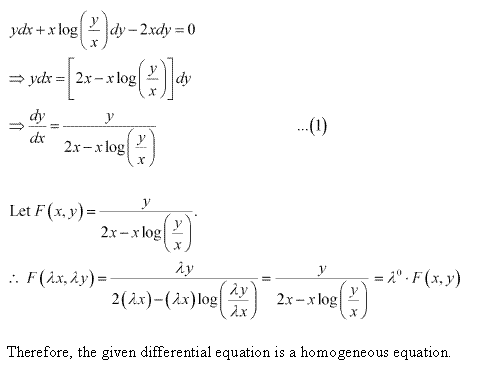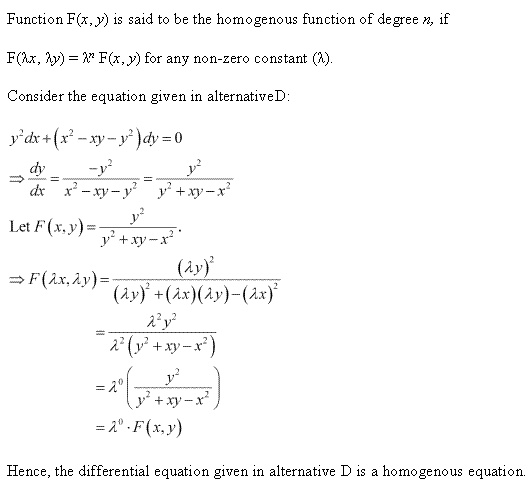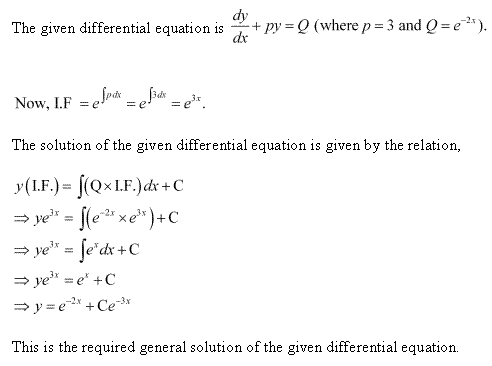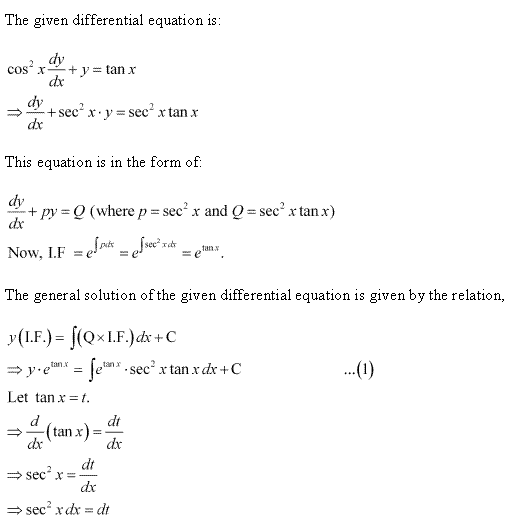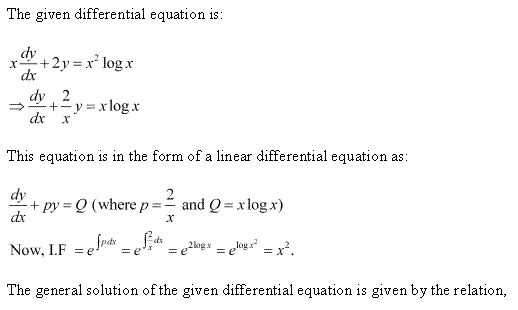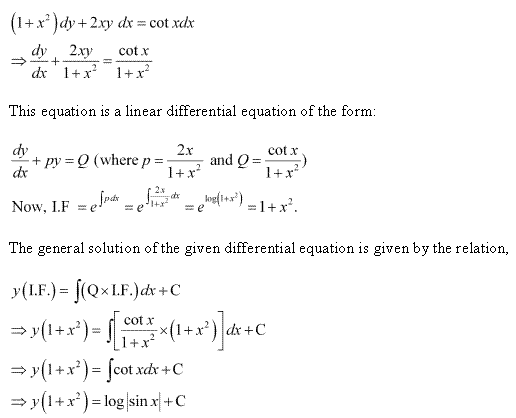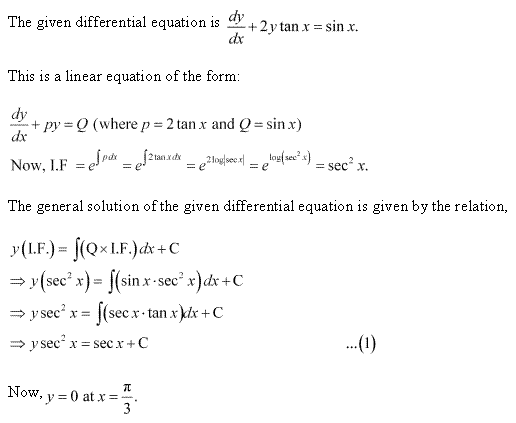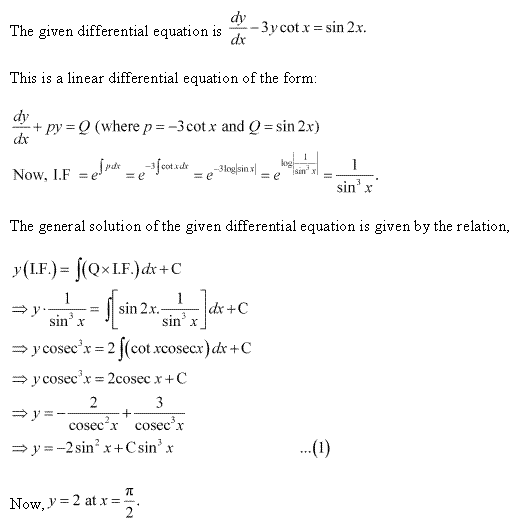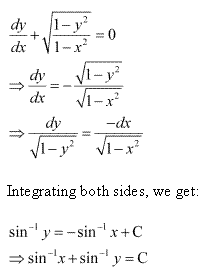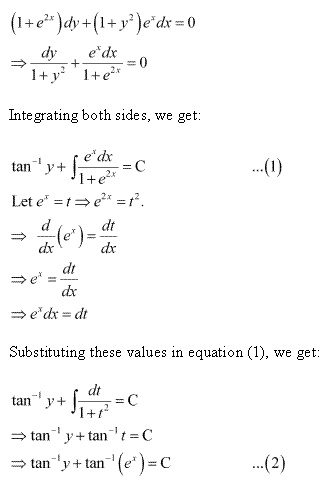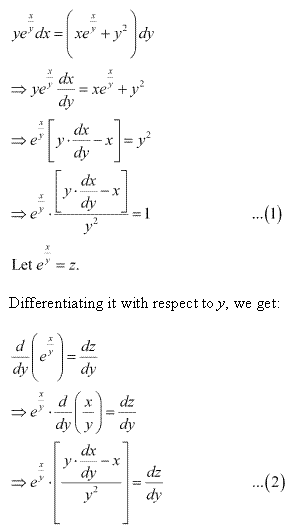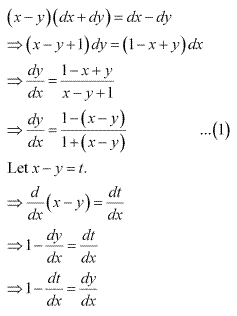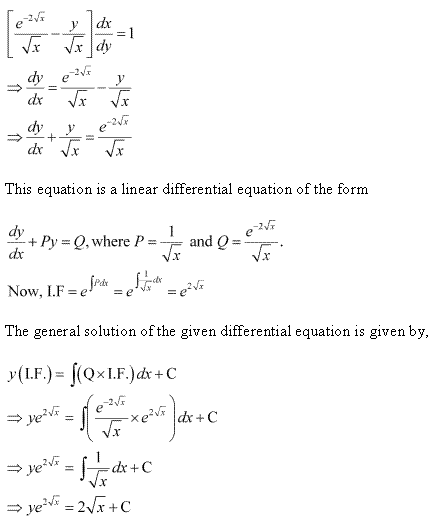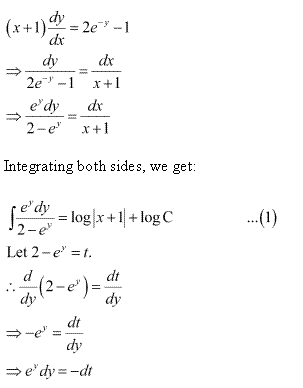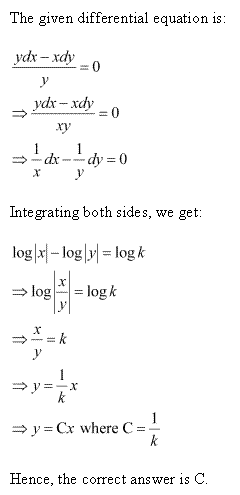Class 12-science NCERT Solutions Maths Chapter 9: Differential Equations
Ex. 9.1
Ex. 9.2
Ex. 9.3
Ex. 9.4
Ex. 9.5
Misc. Ex.
Differential Equations Exercise Ex. 9.1
Solution 1
Solution 2
Solution 3
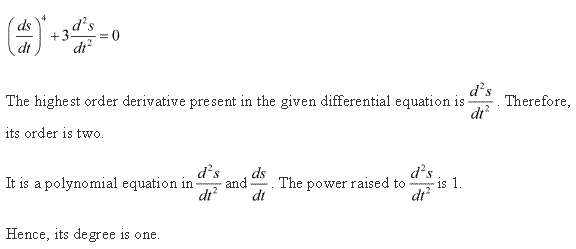
Solution 4
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
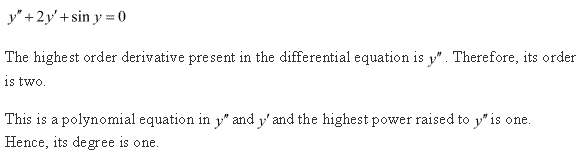
Solution 11
Solution 12
Differential Equations Exercise Ex. 9.2
Solution 1
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
Solution 7
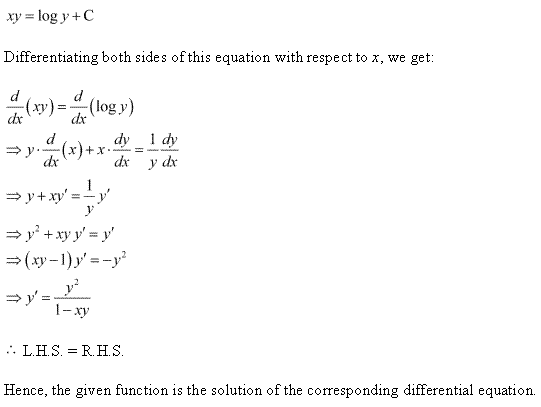
Solution 8
Solution 9
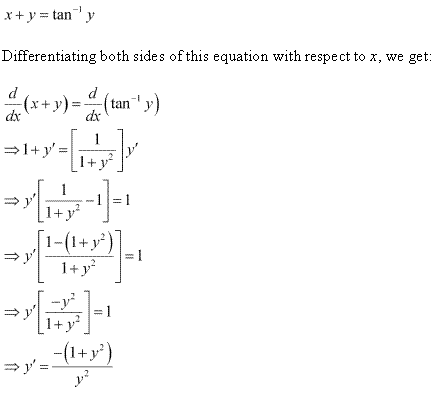
Solution 10
Solution 11
Solution 12
Differential Equations Exercise Ex. 9.3
Solution 1
Solution 2
Solution 3
Solution 4
Solution 5
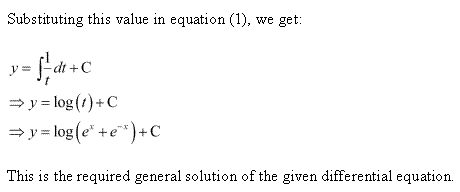
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
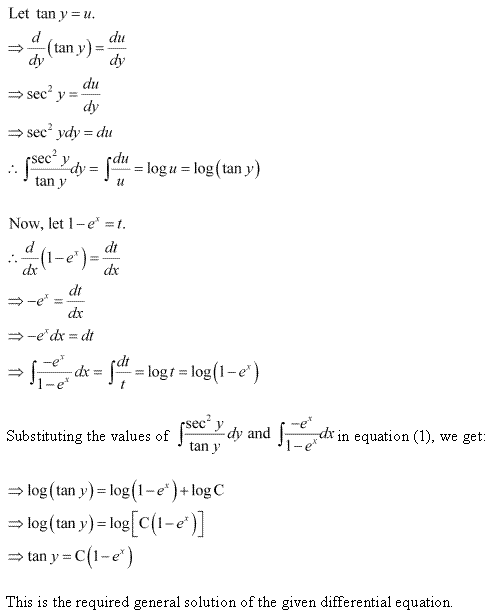
Solution 11
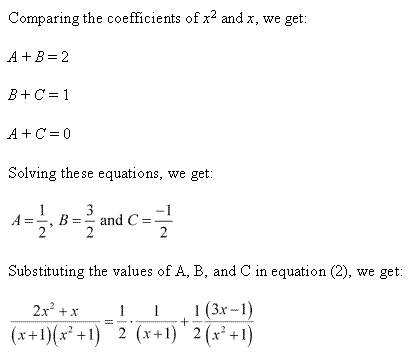
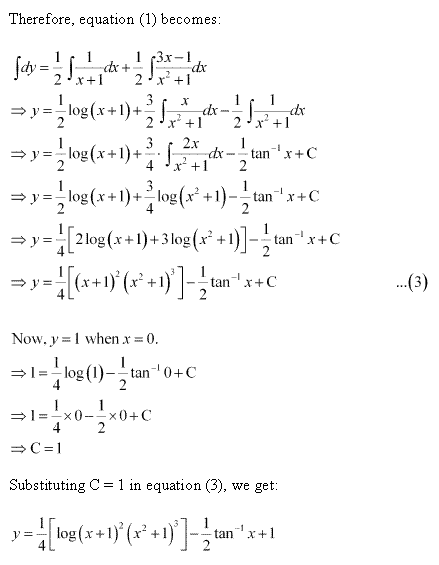
Solution 12
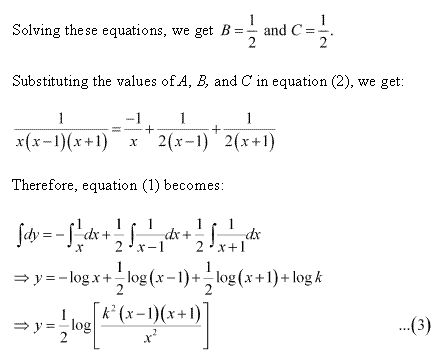
Solution 13
Solution 14
Solution 15
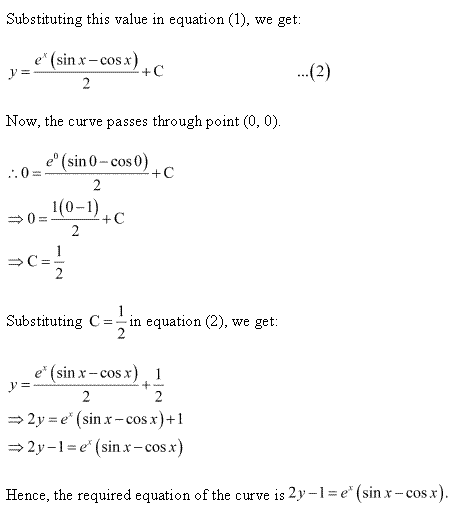
Solution 16
Solution 17
Let x and y be the x-coordinate and y-coordinate of the point on the curve respectively.
We know that the slope of a tangent to the curve in the coordinate axes is given by the relation,
Solution 18
Solution 19
Solution 20
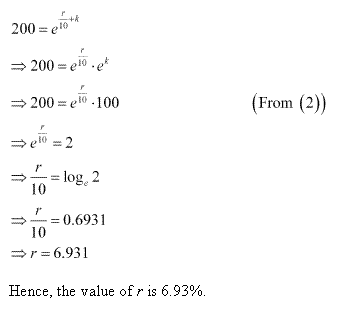
Solution 21
Solution 22
.
.
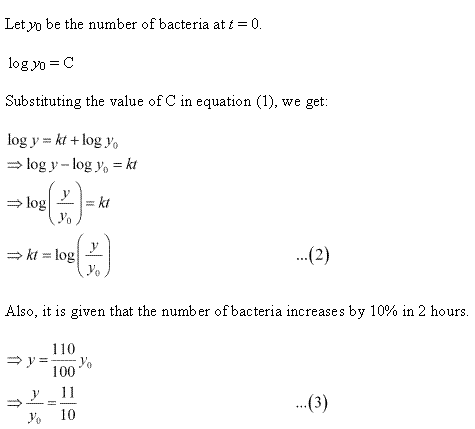
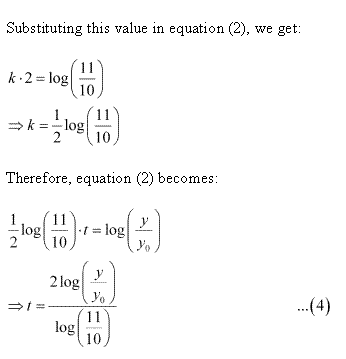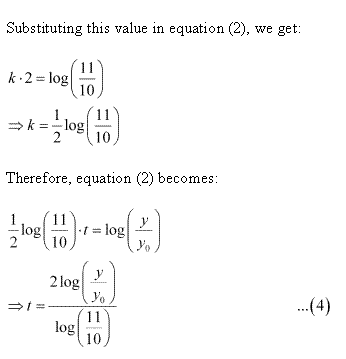.Solution 23
Differential Equations Exercise Ex. 9.4
Solution 1
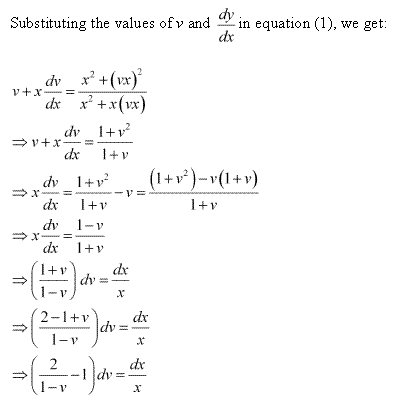
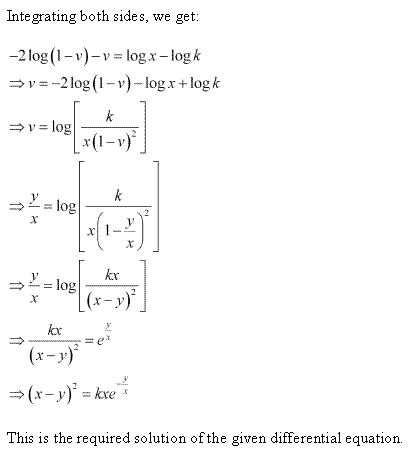
Solution 2
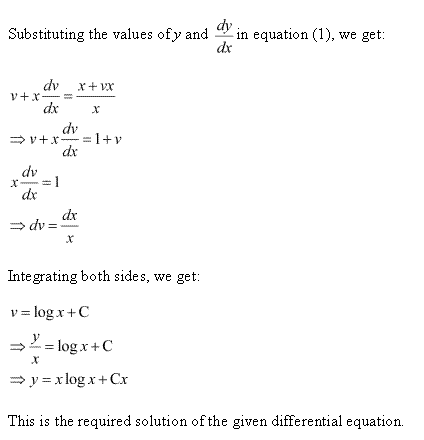
Solution 3
Solution 4
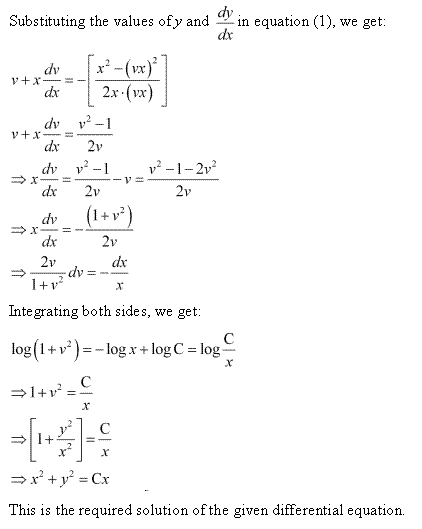
Solution 5
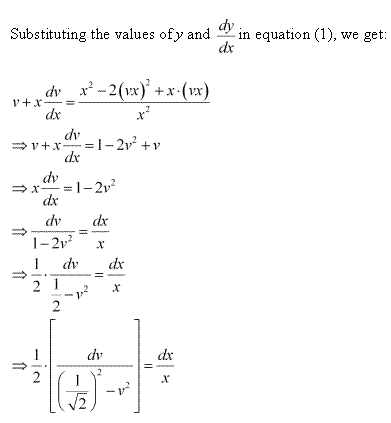
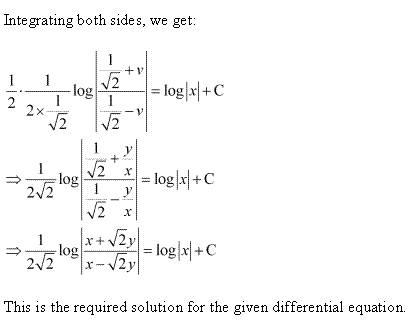
Solution 6
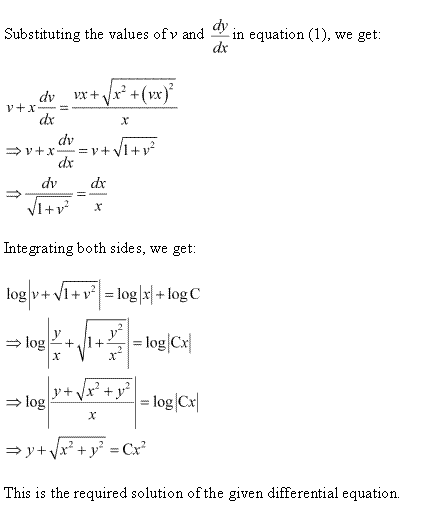
Solution 7
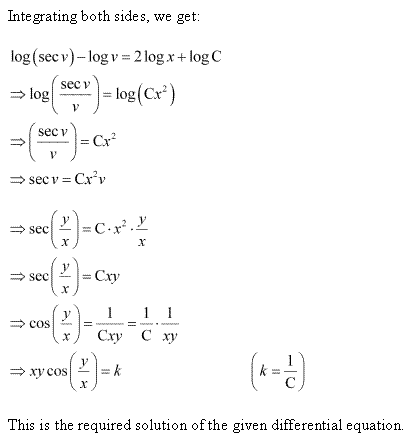
Solution 8
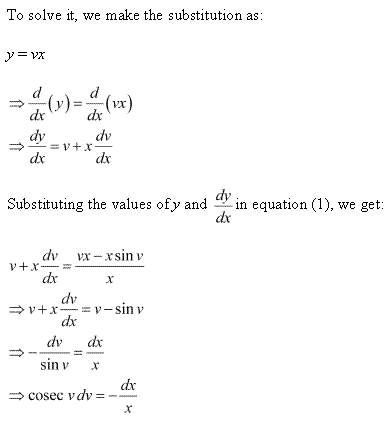
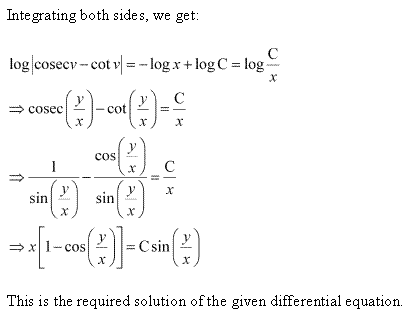
Solution 9
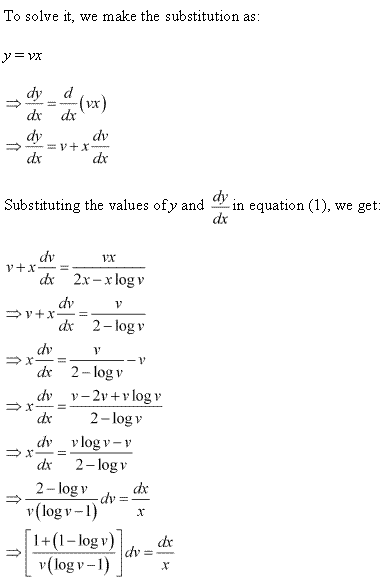
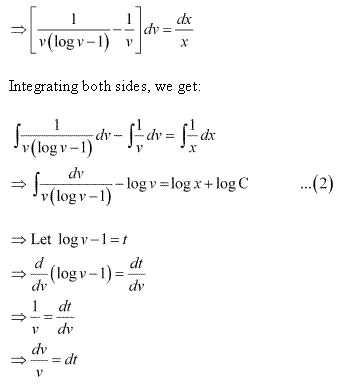
Solution 10
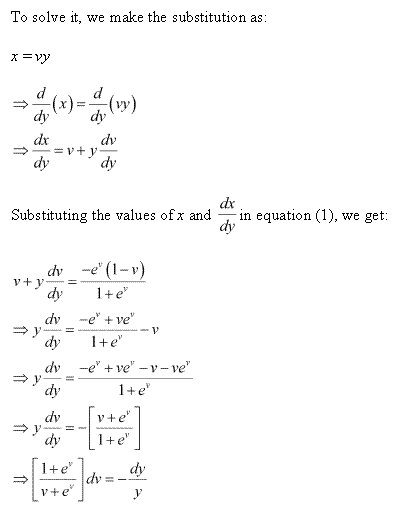
Solution 11
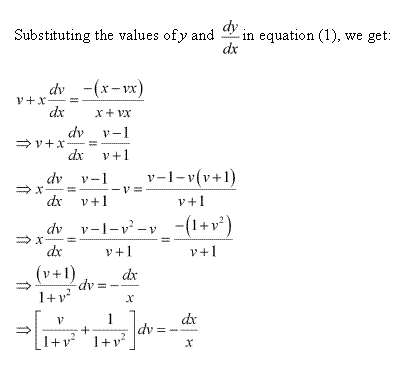
Solution 12
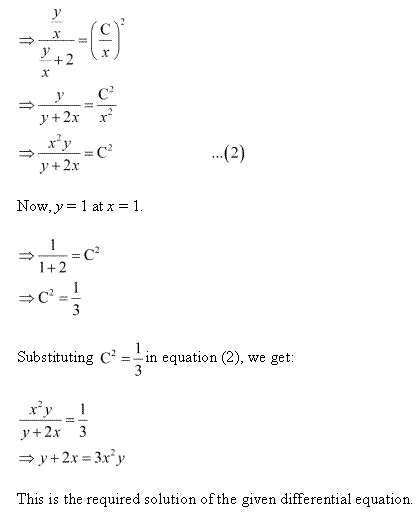
Solution 13
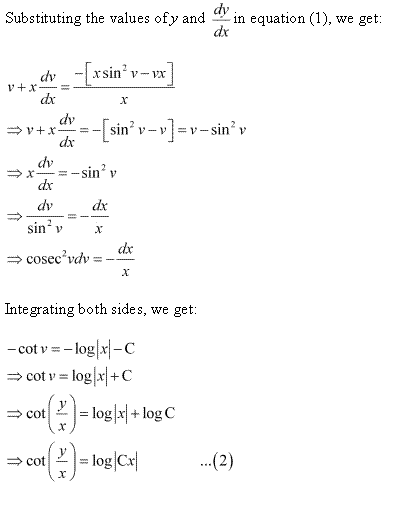
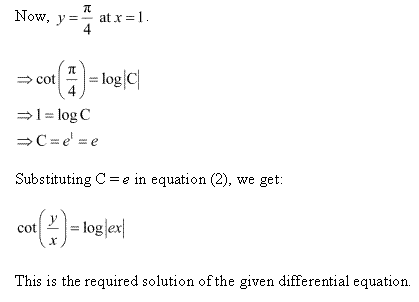
Solution 14
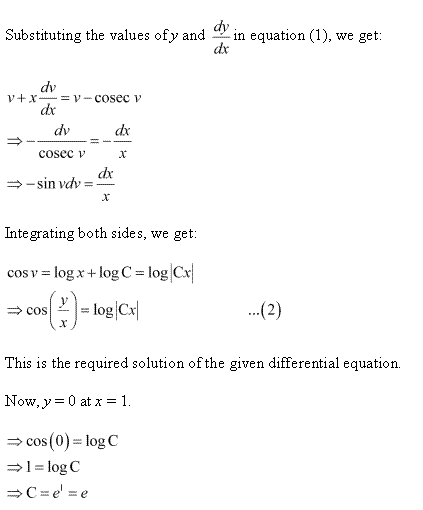
Solution 15
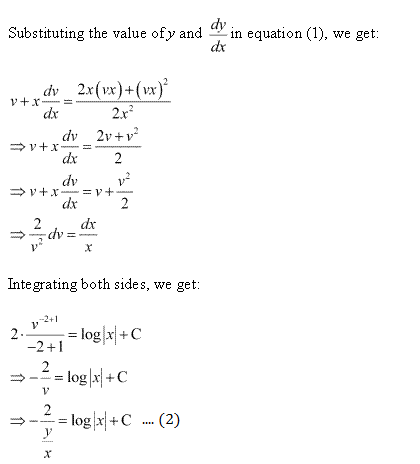
Solution 16
Solution 17
Differential Equations Exercise Ex. 9.5
Solution 1
Solution 2
Solution 3
Solution 4
Solution 5
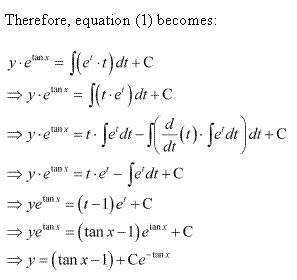
Solution 6
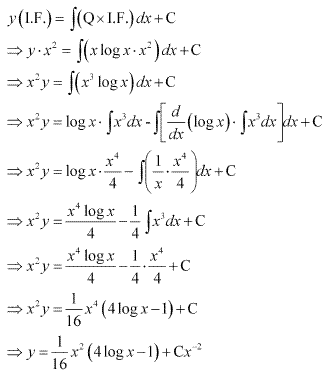
Solution 7
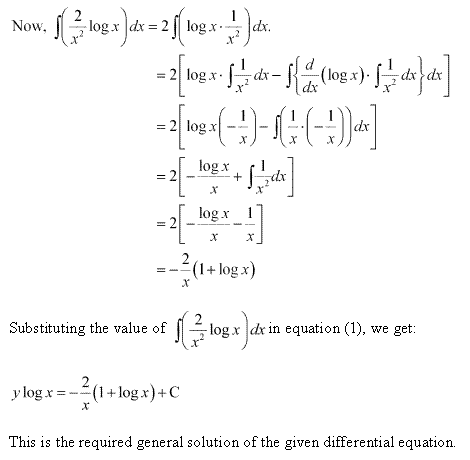
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
Solution 13
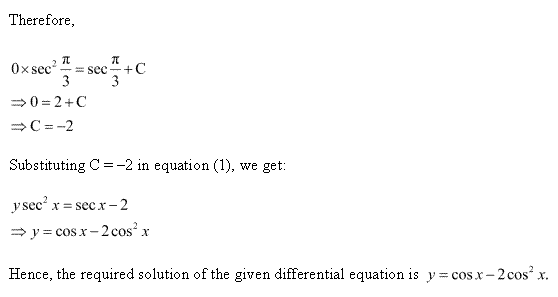
Solution 14
Solution 15
Solution 16
Solution 17
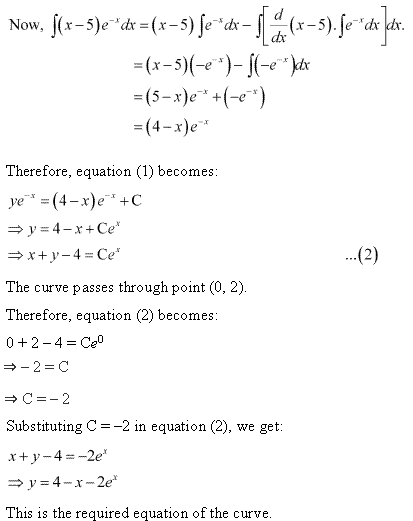
Solution 18
Solution 19
Differential Equations Exercise Misc. Ex.
Solution 1
Solution 2
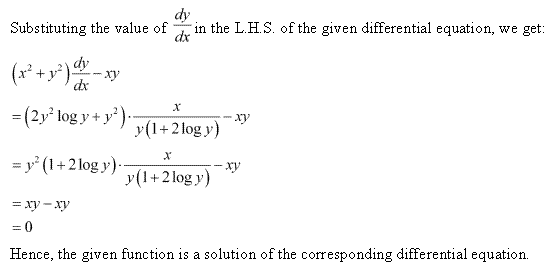
Solution 3
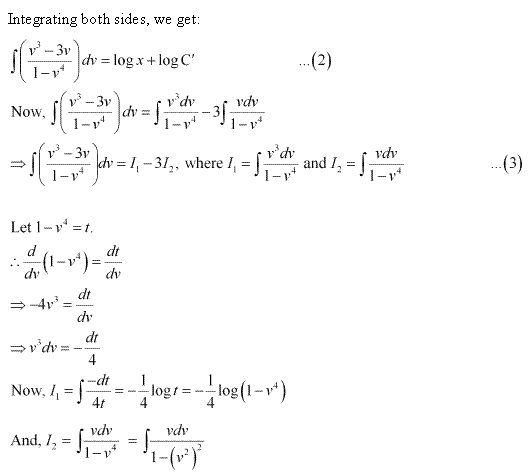
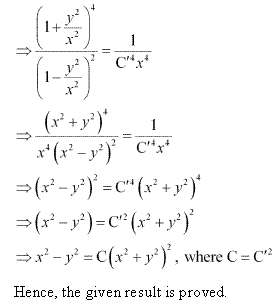
Solution 4
Solution 5
Solution 6
Solution 7
Solution 8
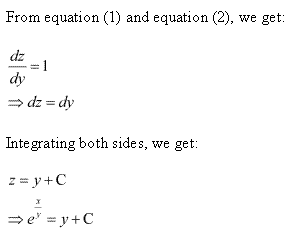
Solution 9
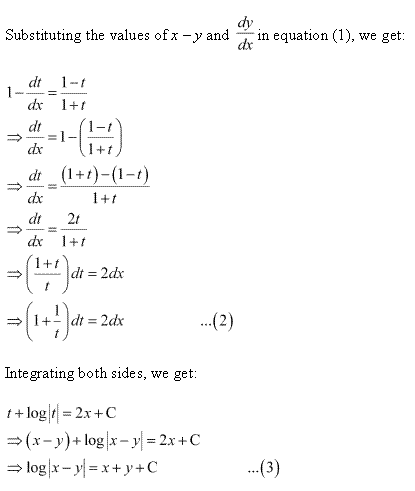
Solution 10
Solution 11
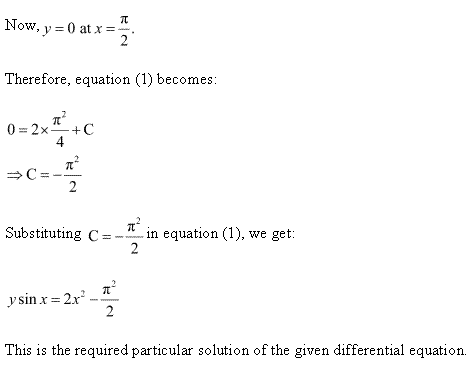
Solution 12
Solution 13
Solution 14
Solution 15
