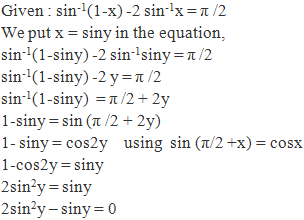Class 12-commerce NCERT Solutions Maths Chapter 2: Inverse Trigonometric Functions
Ex. 2.1
Ex. 2.2
Misc. Ex.
Inverse Trigonometric Functions Exercise Ex. 2.1
Solution 1

Solution 2

Solution 3
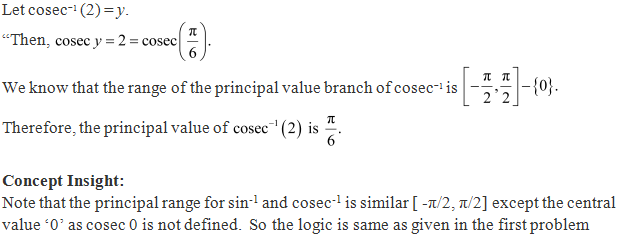
Solution 4

Solution 5
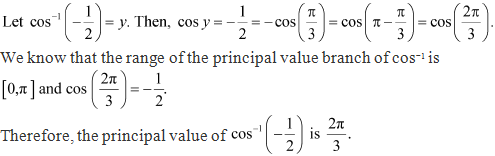
Solution 6
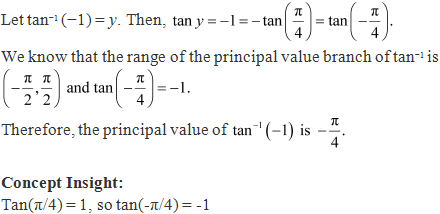
Solution 7

We know that the range of the principal value of sec-1 is
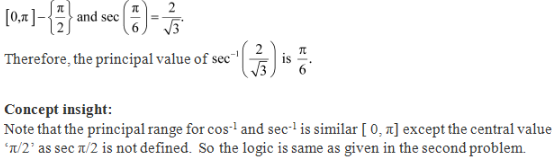
Solution 8

Solution 9

Solution 10
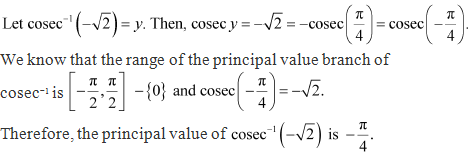
Solution 11
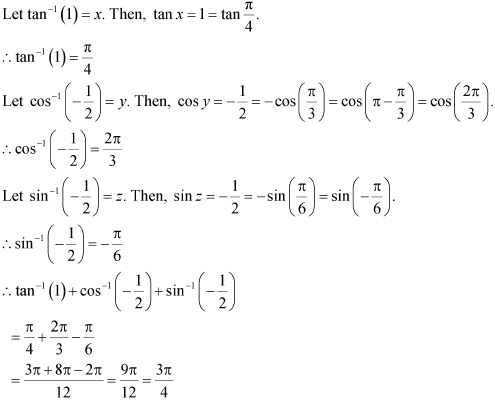
Solution 12
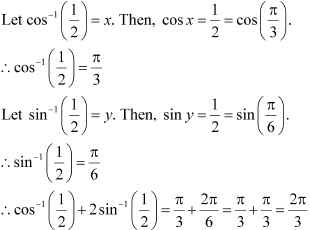
Solution 13

Solution 14
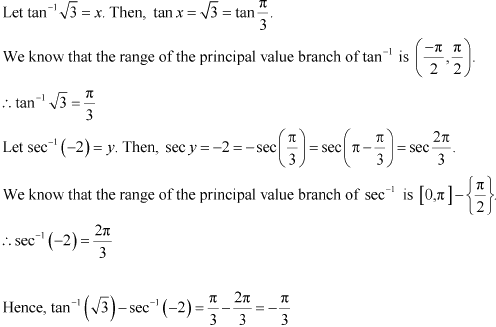

Inverse Trigonometric Functions Exercise Ex. 2.2
Solution 1
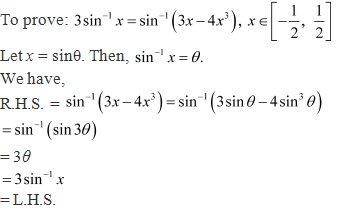
![]()
Solution 2

Solution 3

Solution 4

Solution 5

Solution 6

Solution 7
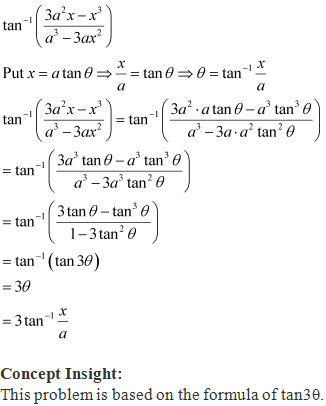
Solution 8
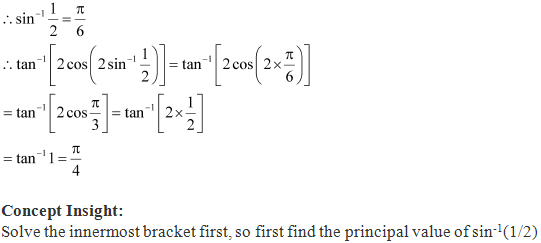
Solution 9

Solution 10

Solution 11

Solution 12
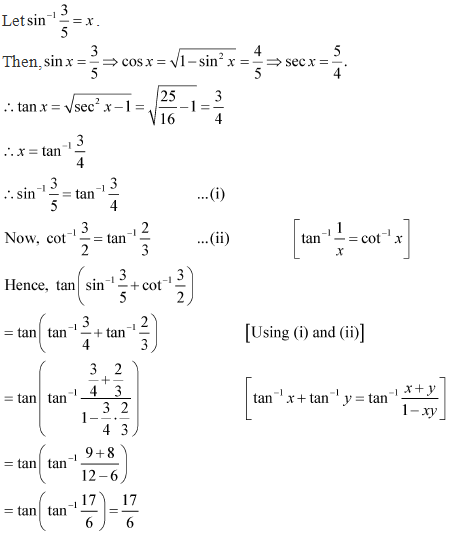
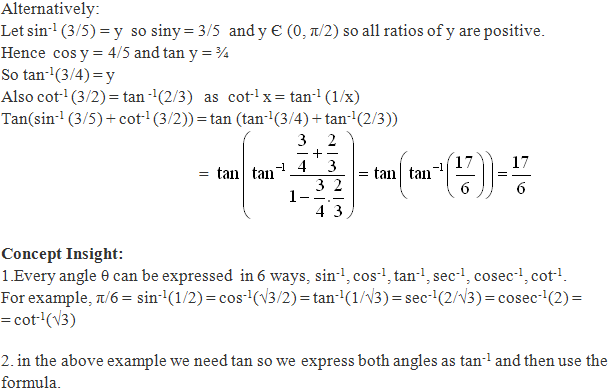
Solution 13

Solution 14

Solution 15
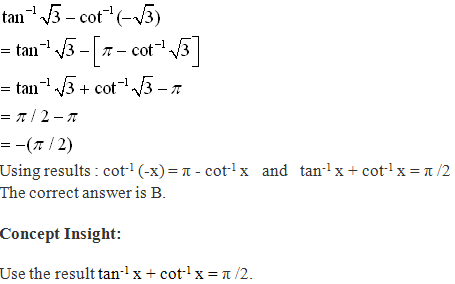
Inverse Trigonometric Functions Exercise Misc. Ex.
Solution 1

Solution 2
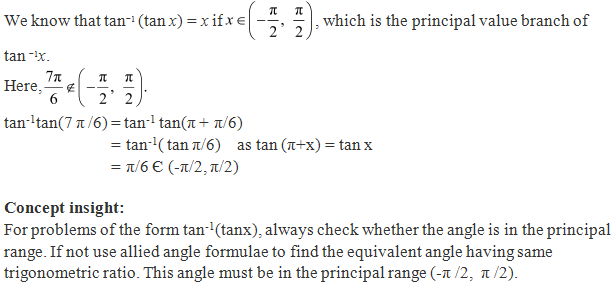
Solution 3
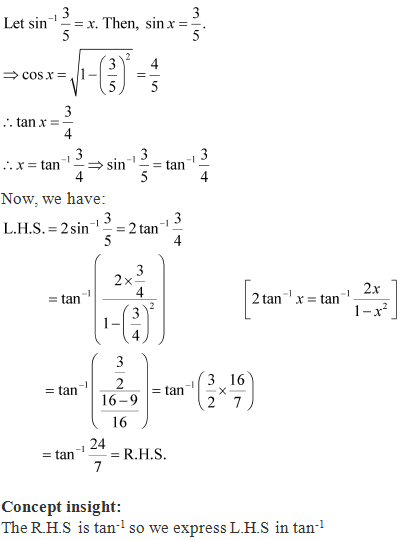
Solution 4
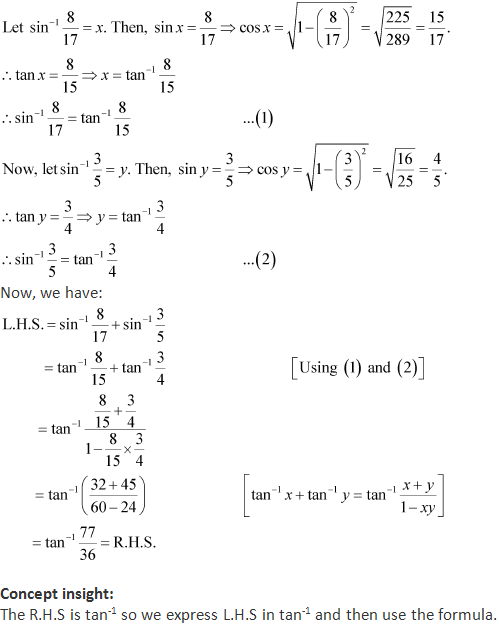
Solution 5
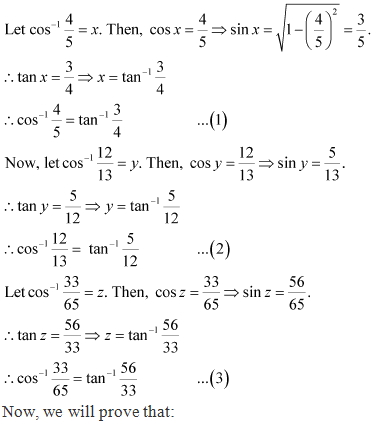
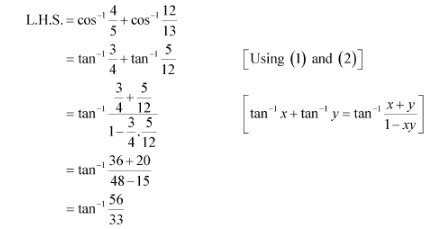
= ![]() by (3)
by (3)
= RHS

Solution 6
Let sin-1(3/5) = A and cos-1 (12/13) = B
So sin A = 3/5 and cos B = 12/13
Hence cos A = 4/5 and sin B = 5/13
As R.H.S is sin-1 we use sin (A + B)
Sin (A + B) = sin A cos B + cos A sin B = (3/5) (12/13) + (4/5) (5/13)
= 36/65 + 20/65 = 56/65
Thus A + B = sin-1 (56/65) hence proved.
Concept insight:
If R.H.S is cos-1 or sin-1 then use Cos (A + B) or sin (A + B) as the case may be.
Solution 7
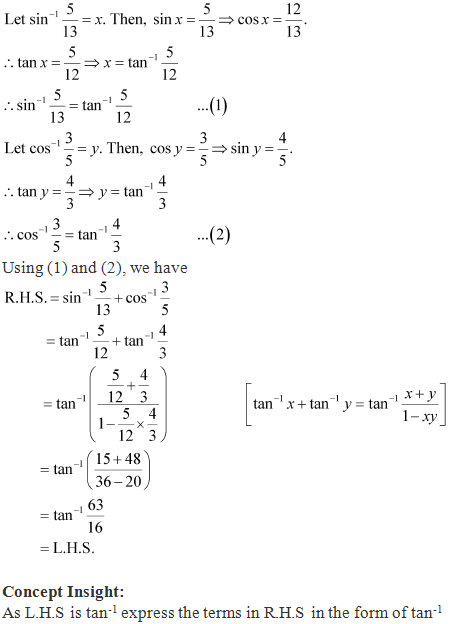
Solution 8
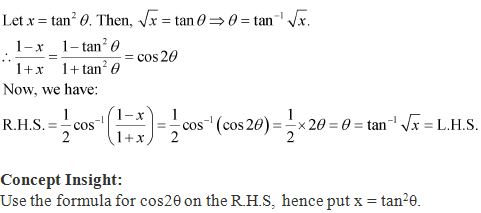
Solution 9

Solution 10

Solution 11
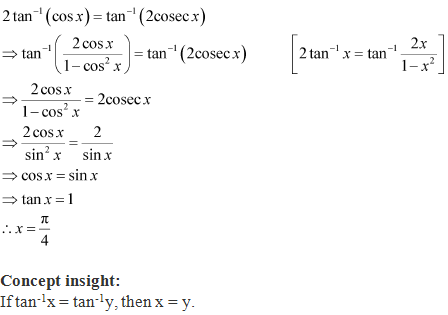
Solution 12
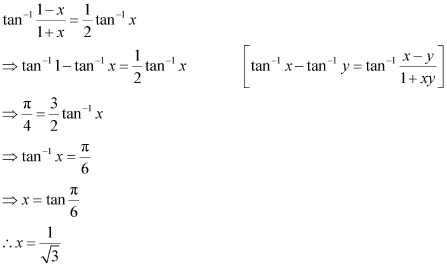
Solution 13
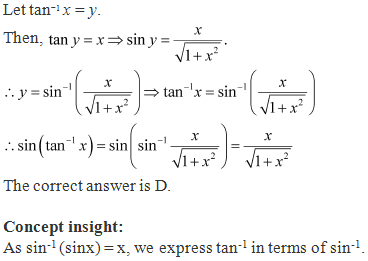
Solution 14