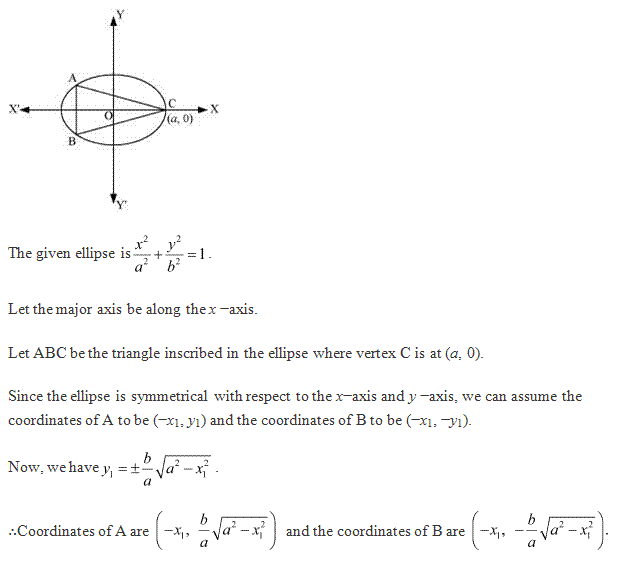
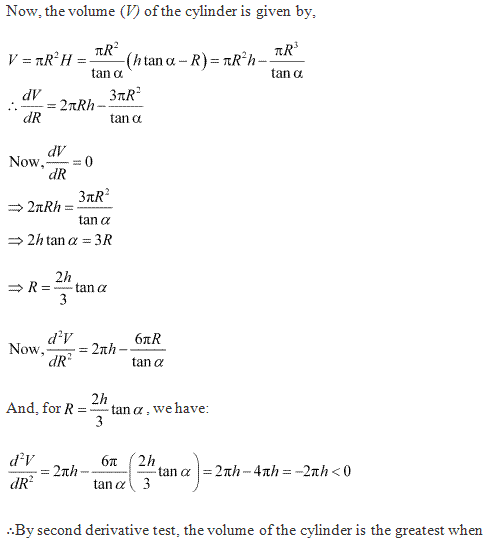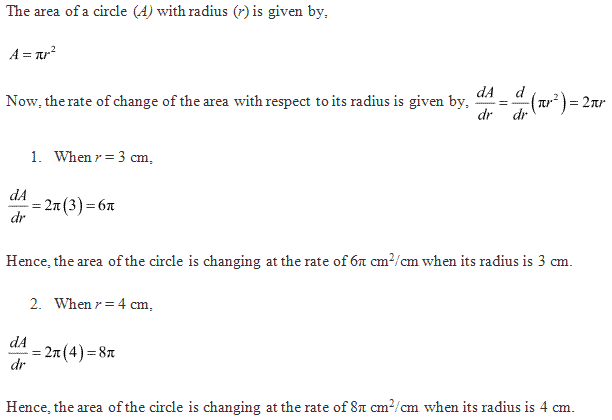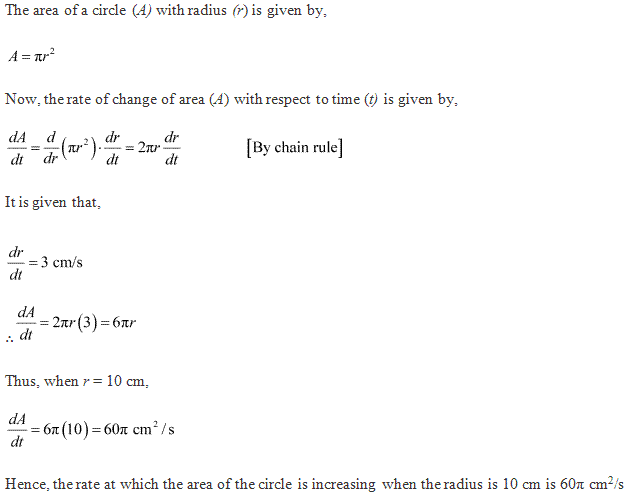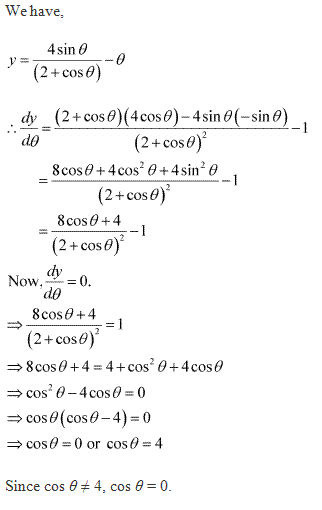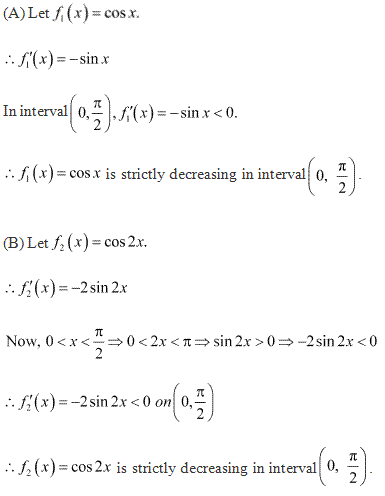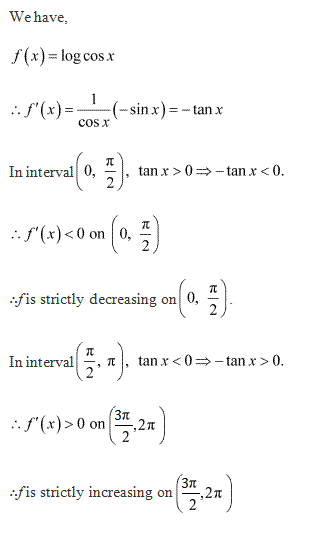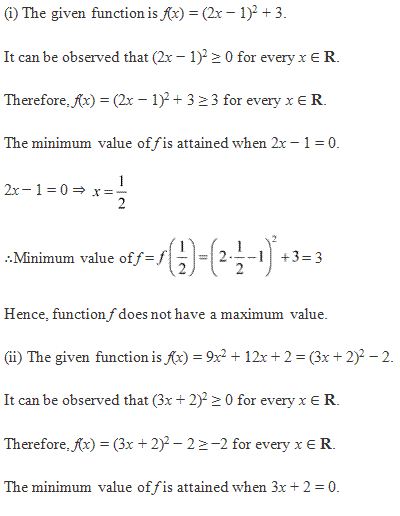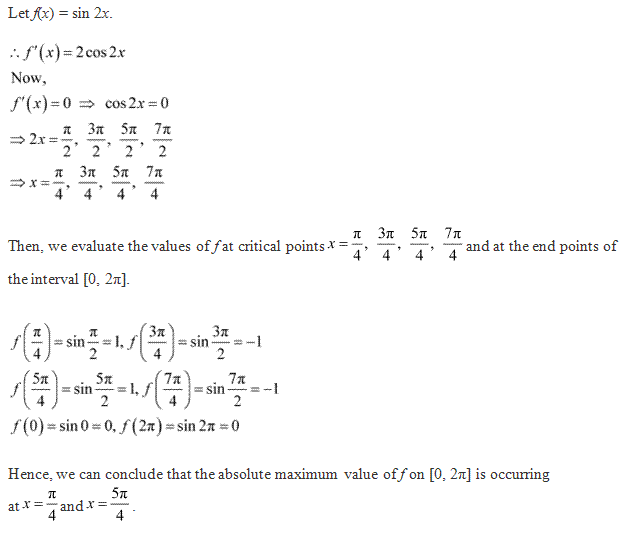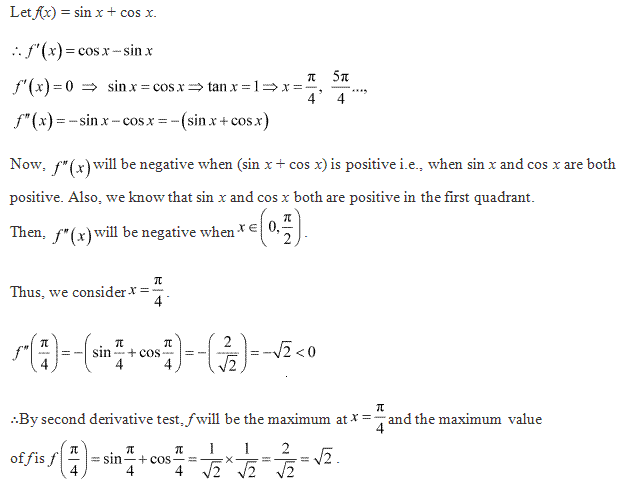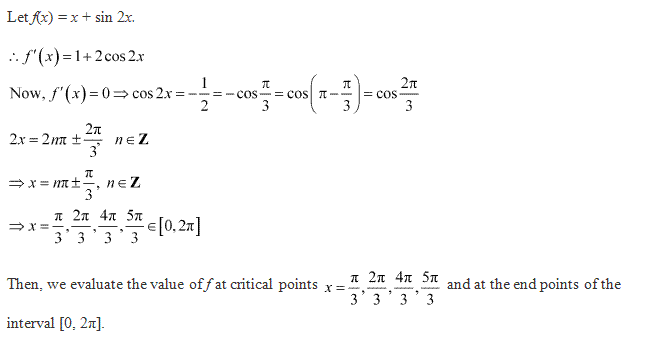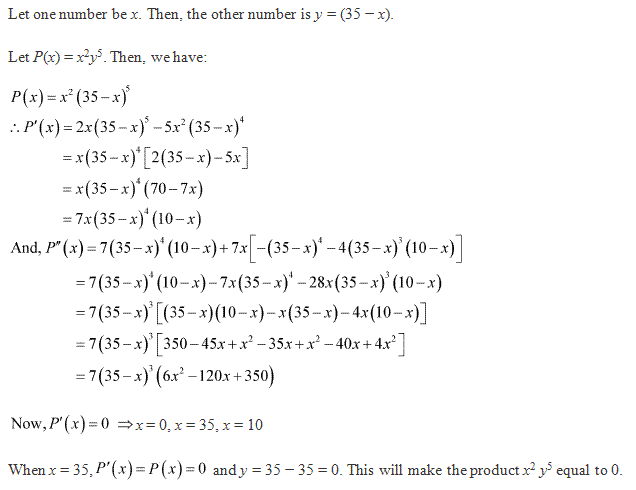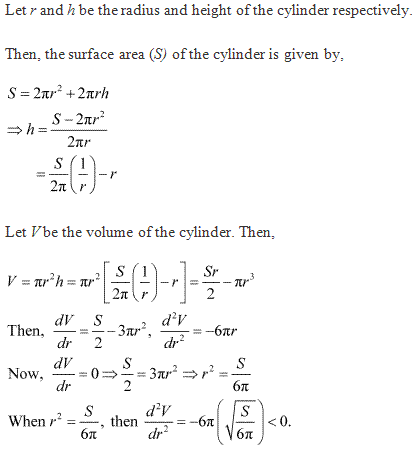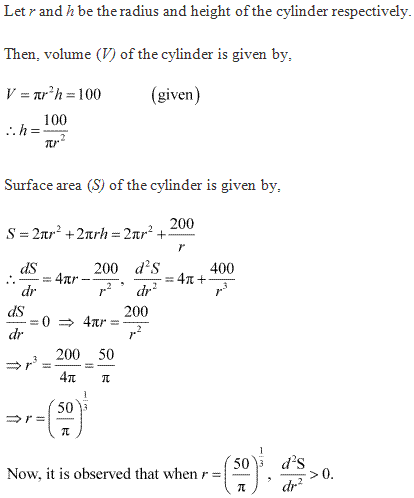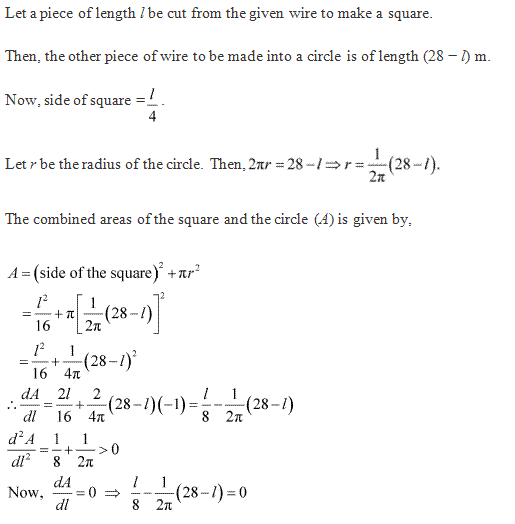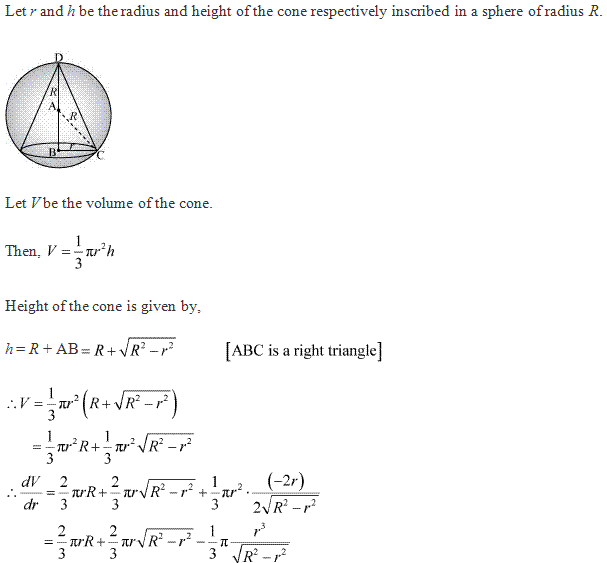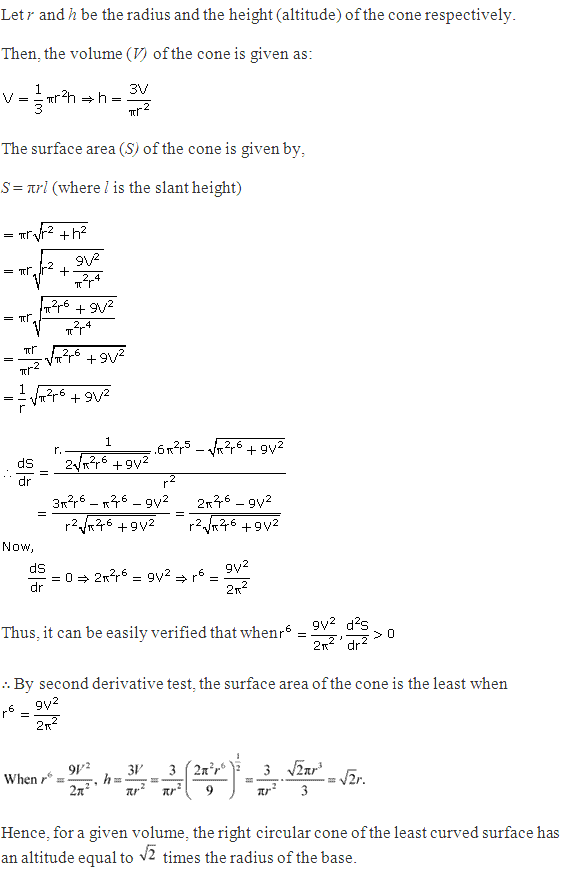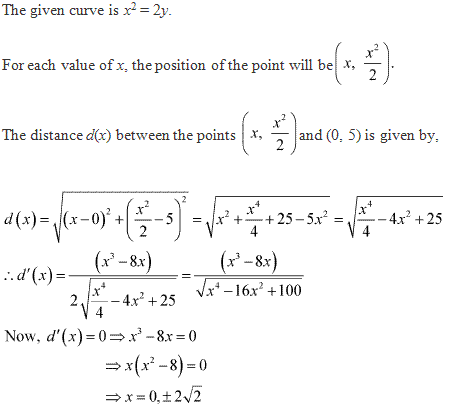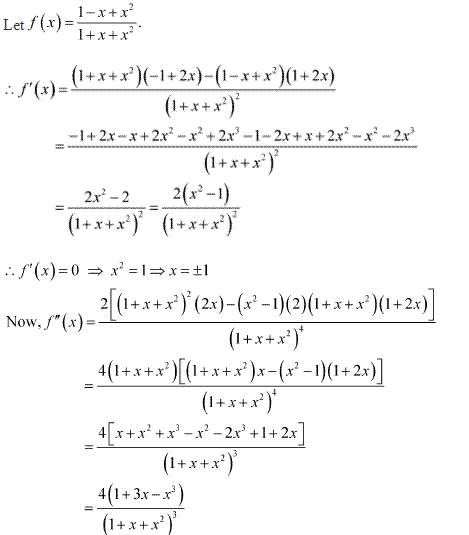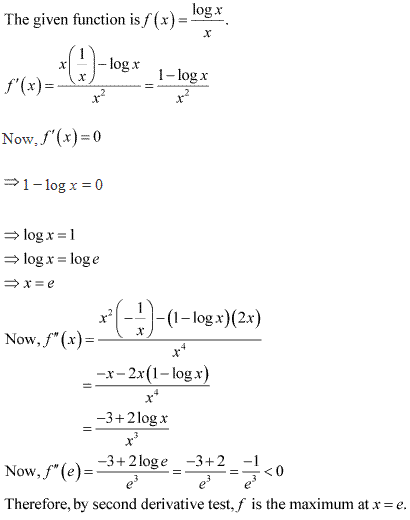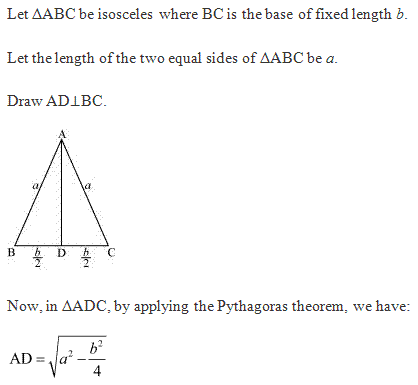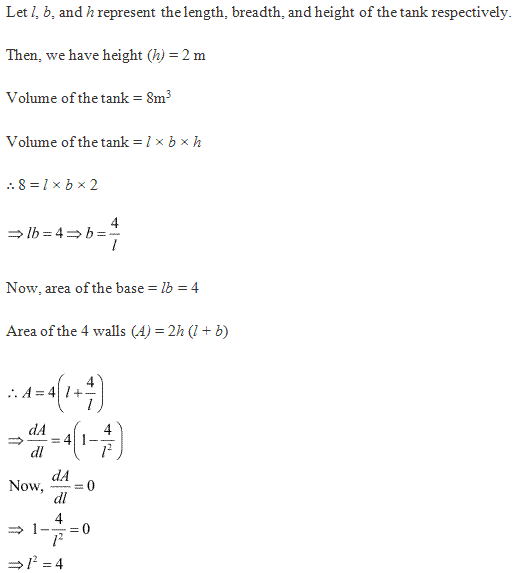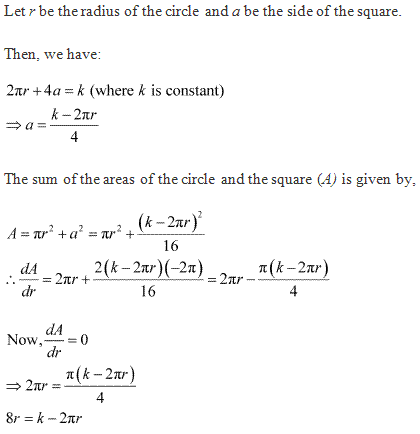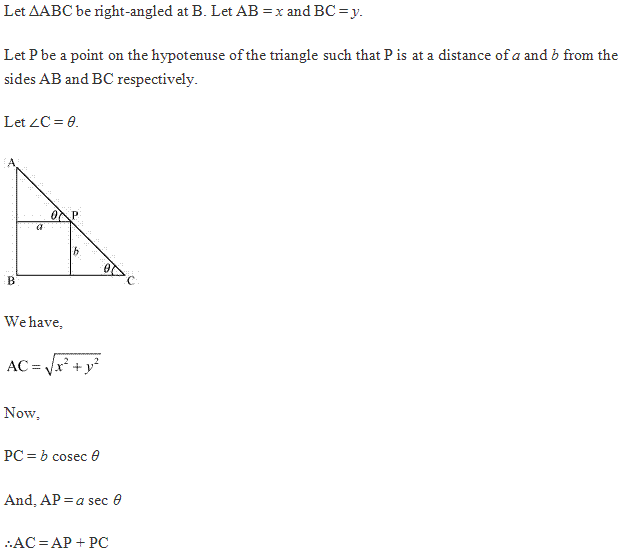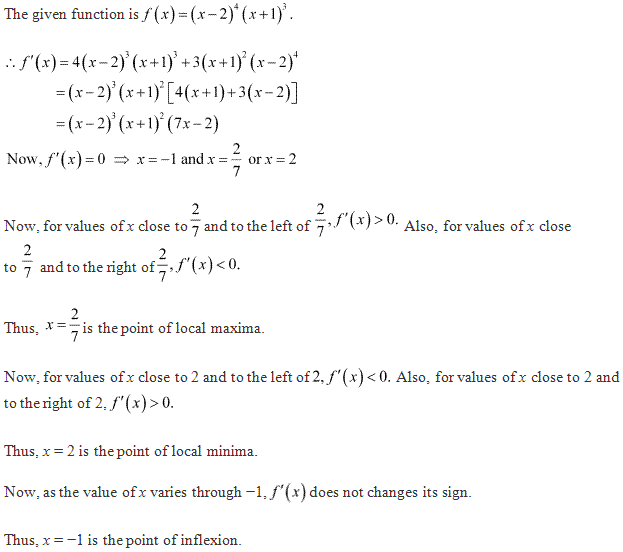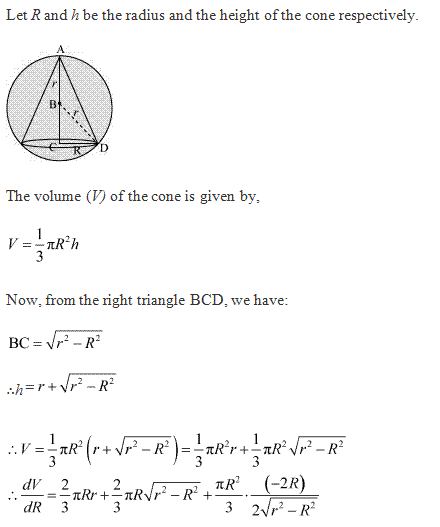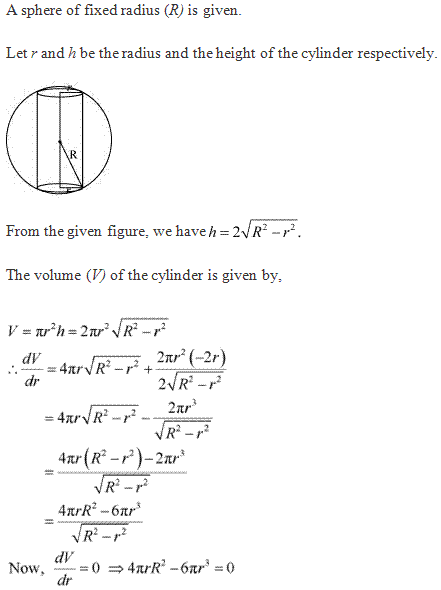Class 12-commerce NCERT Solutions Maths Chapter 6: Applications of Derivatives
Ex. 6.1
Ex. 6.2
Ex. 6.3
Misc. Ex.
Applications of Derivatives Exercise Ex. 6.1
Solution 1
Solution 2
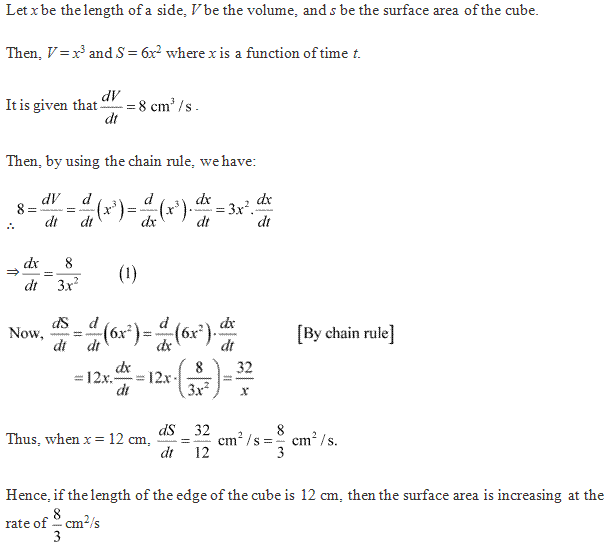
Solution 3
Solution 4

Solution 5

Solution 6

Solution 7

Solution 8


Solution 9
Solution 10

Solution 11

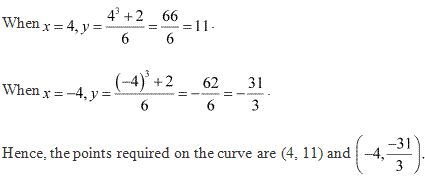
Solution 12
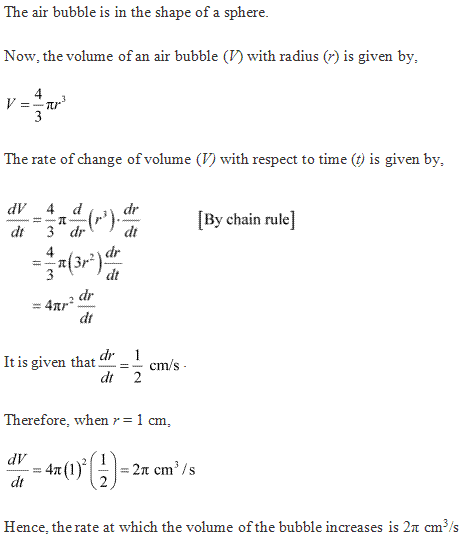
Solution 13

Solution 14


Solution 15
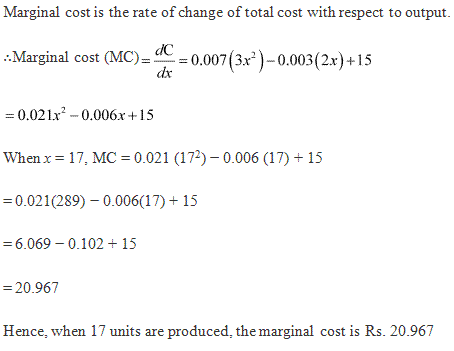
Solution 16
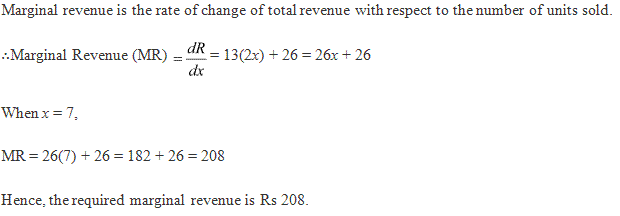
Solution 17

Solution 18

Applications of Derivatives Exercise Ex. 6.2
Solution 1
Solution 2
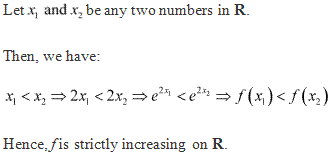
Solution 3
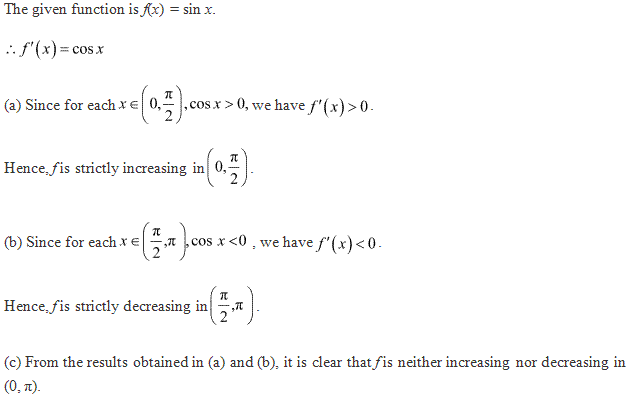
Solution 4
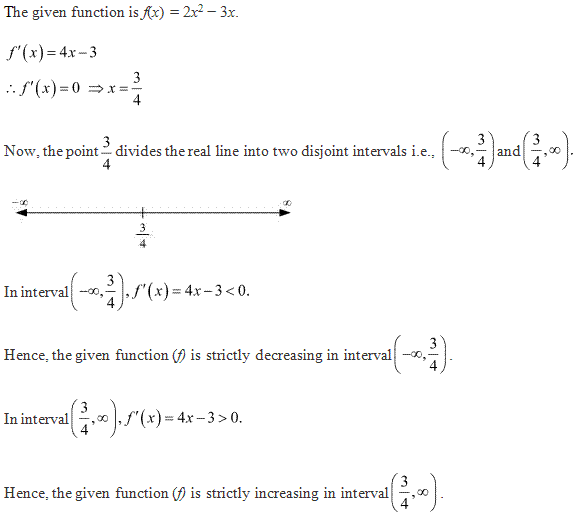
Solution 5

Solution 6



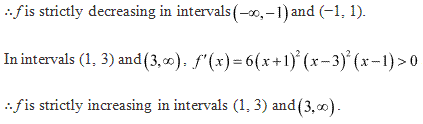
Solution 7
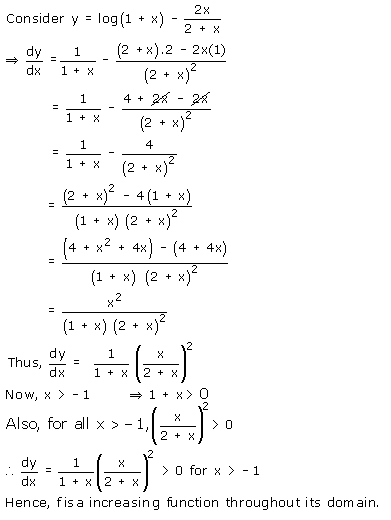
Solution 8

Solution 9
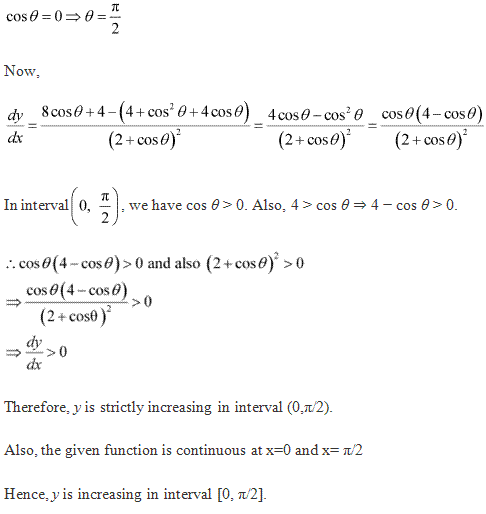
Solution 10
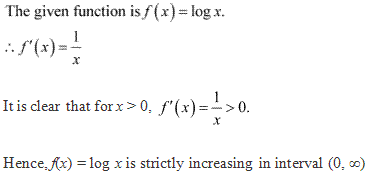
Solution 11

Solution 12

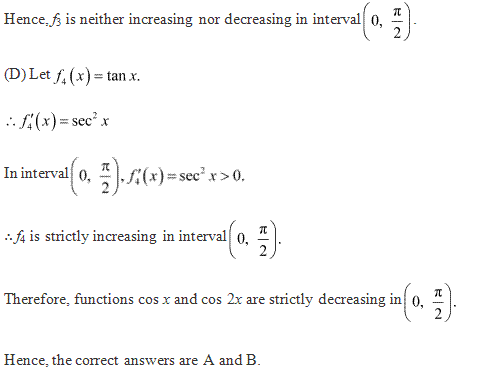
Solution 13
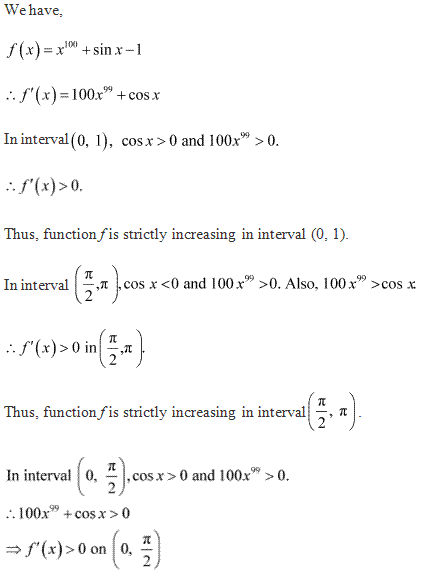
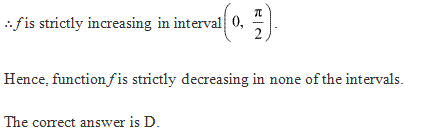
Solution 14
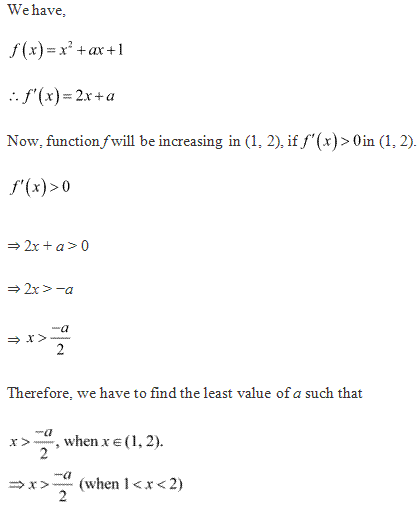
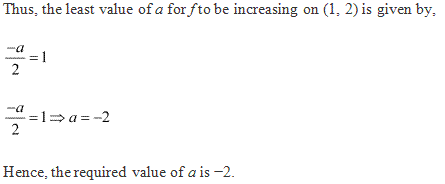
Solution 15


Solution 16
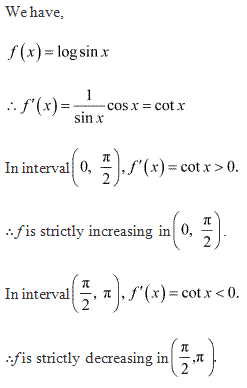
Solution 17
Solution 18
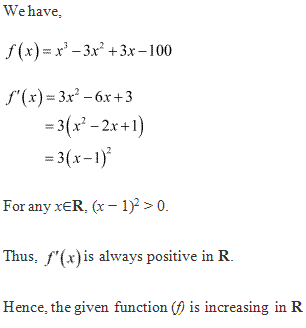
Solution 19

Applications of Derivatives Exercise Ex. 6.3
Solution 1

Solution 2

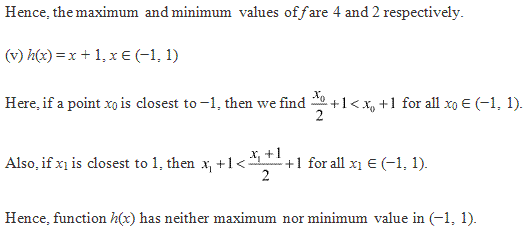
Solution 3




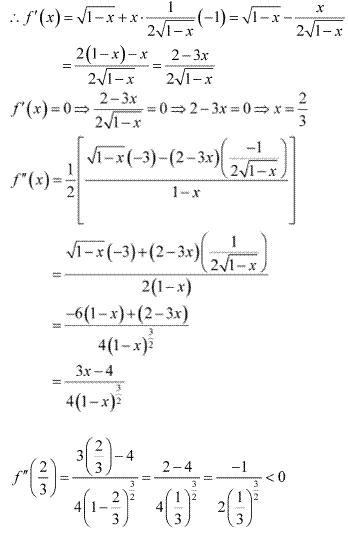
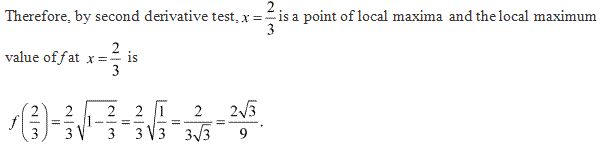
Solution 4
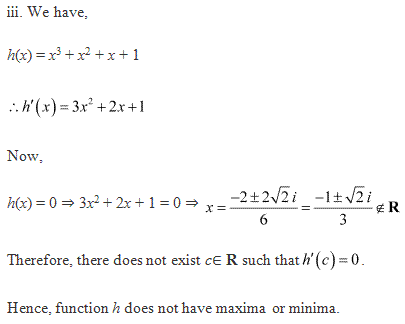
Solution 5


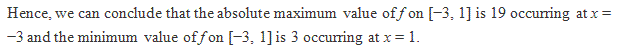
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
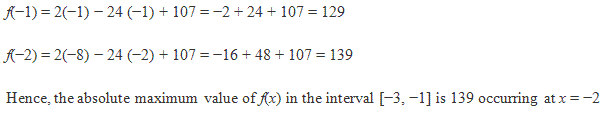
Solution 11
Solution 12

Solution 13
Solution 14
Solution 15

Solution 16
Solution 17

Solution 18
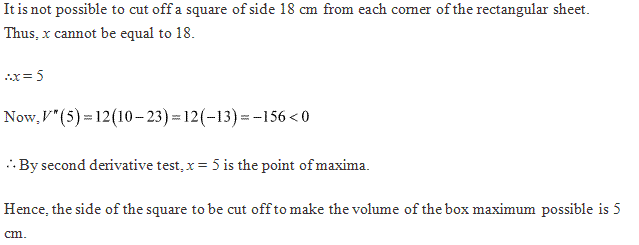
Solution 19

Solution 20
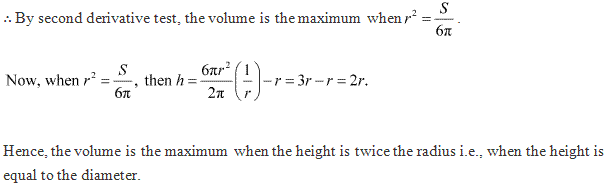
Solution 21

Solution 22
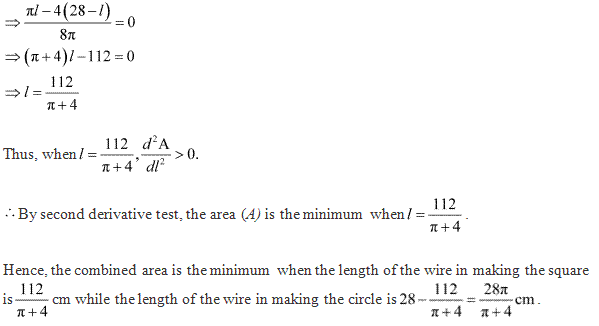
Solution 23
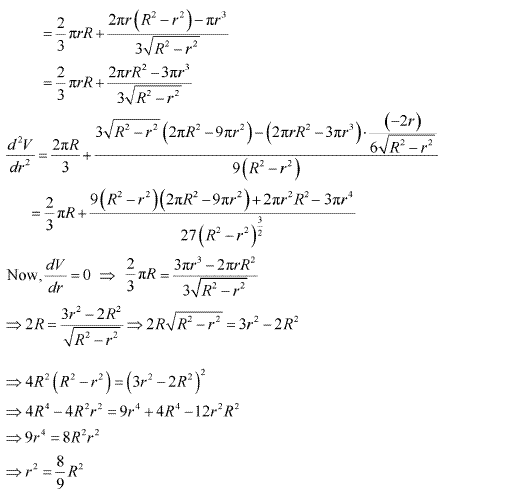
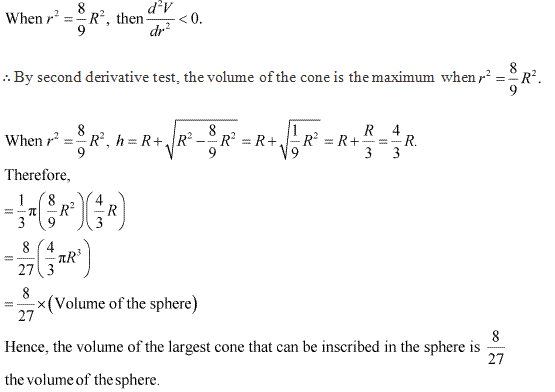
Solution 24
Solution 25

Solution 26
Solution 27
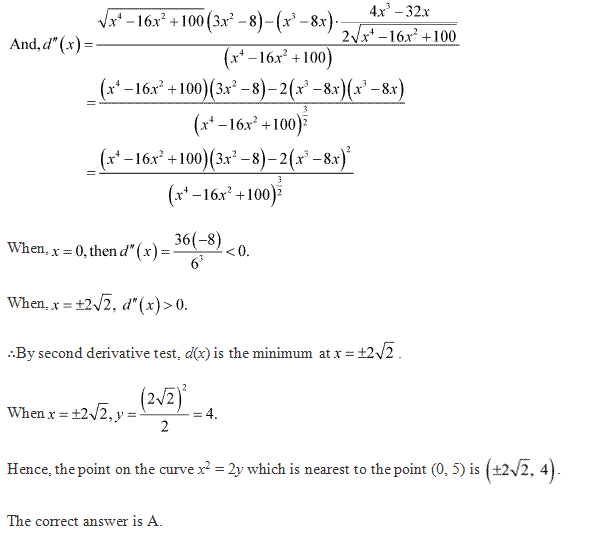
Solution 28
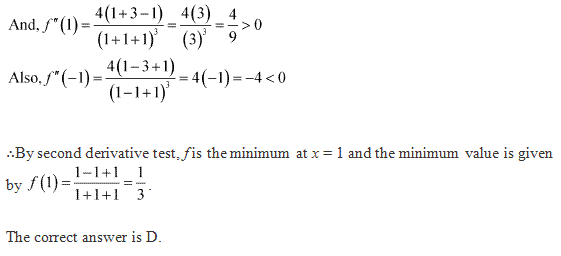
Solution 29
Applications of Derivatives Exercise Misc. Ex.
Solution 1
Solution 2
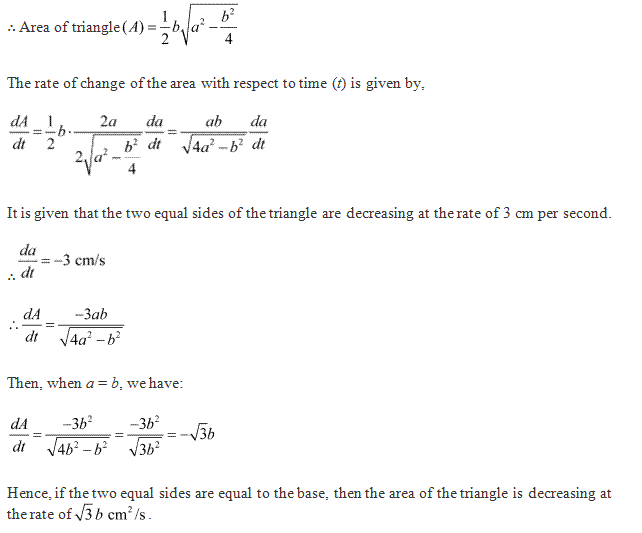
Solution 3
Solution 4
Solution 5
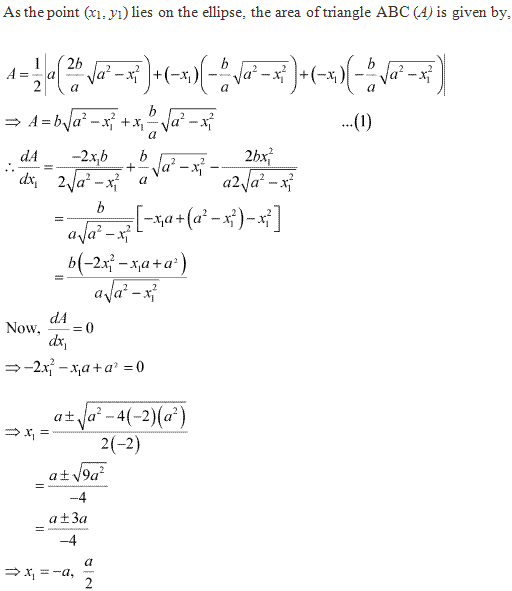

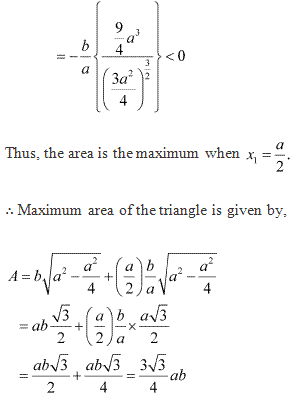
Solution 6

Solution 7

Solution 8
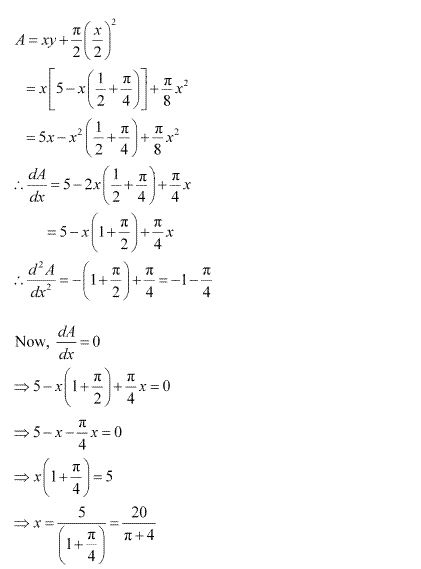

Solution 9

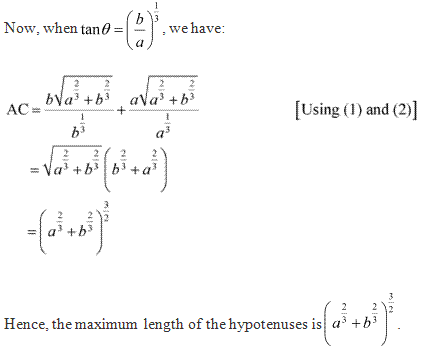
Solution 10
Solution 11
Solution 12


Solution 13
Solution 14

Solution 15