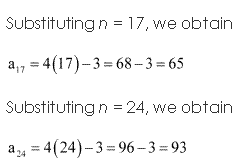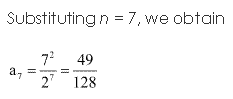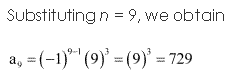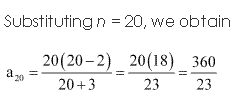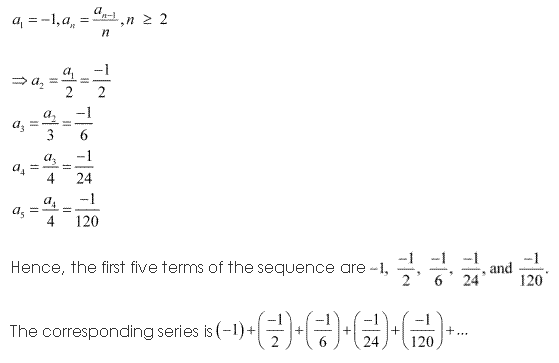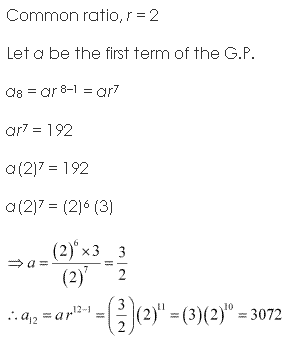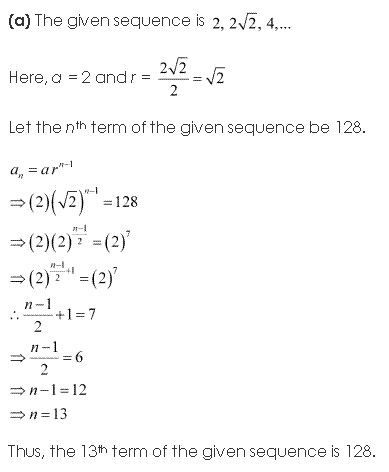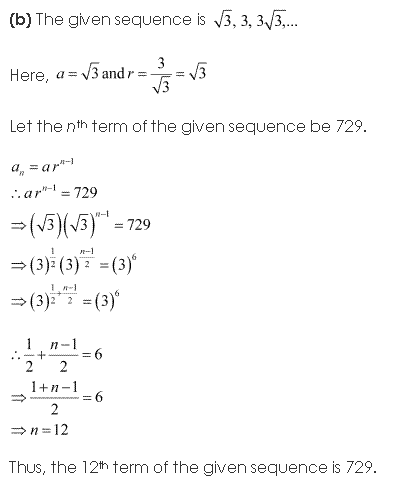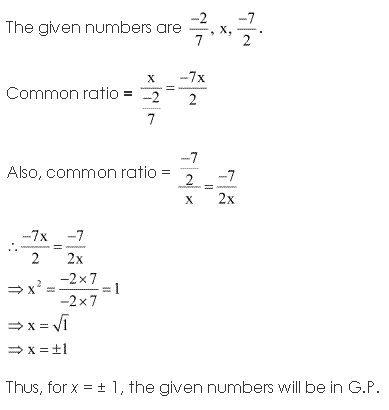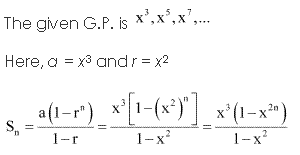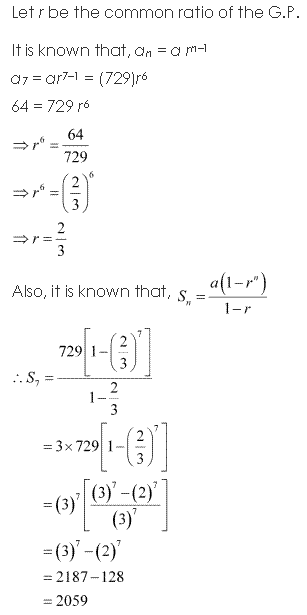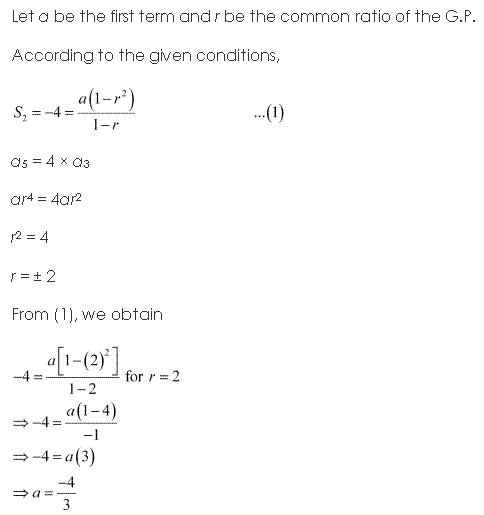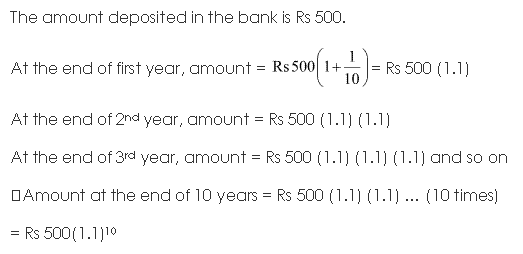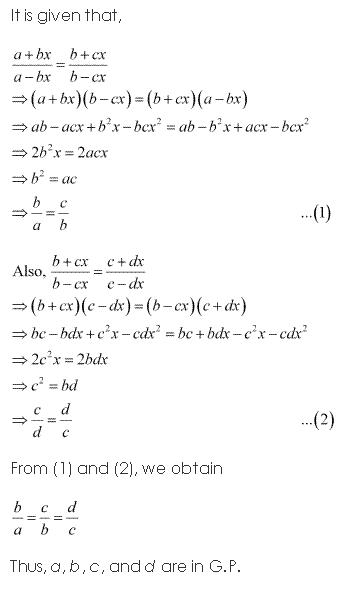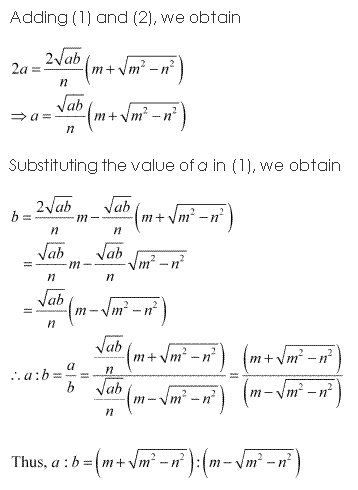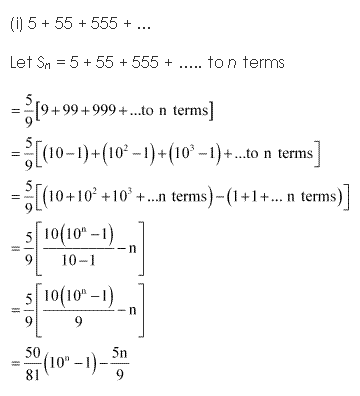Class 11-commerce NCERT Solutions Maths Chapter 8: Sequences and Series
Sequences and Series Exercise Ex. 8.1
Solution 1
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
Solution 13
Solution 14
Sequences and Series Exercise Ex. 8.2
Solution 1
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
Solution 13
Solution 14
Solution 15
Solution 16
Solution 17
Solution 18
Solution 19
Solution 20
Solution 21
Solution 22
Solution 23
Solution 24
Solution 25
a, b, c, d are in G.P.
Therefore,
bc = ad .....(1)
b2 = ac .....(2)
c2 = bd .....(3)
It has to be proved that,
(a2 + b2 + c2) (b2 + c2 + d2) = (ab + bc + cd)2
R.H.S.
= (ab + bc + cd)2
= (ab + ad + cd)2 [Using (1)]
= [ab + d (a + c)]2
= a2b2 + 2abd (a + c) + d2(a + c)2
= a2b2 + 2a2bd + 2abcd + d2(a2 + 2ac + c2)
= a2b2 + 2a2c2 + 2b2c2 + d2a2 + 2d2b2 + d2c2 [Using (1) and (2)]
= a2b2 + a2c2 + a2c2 + b2c2 + b2c2 + d2a2 + d2b2 + d2b2 + d2c2
= a2b2 + a2c2 + a2d2 + b2 × b2 + b2c2 + b2d2 + c2b2 + c2 × c2 + c2d2
[Using (2) and (3) and rearranging terms]
= a2(b2 + c2 + d2) + b2(b2 + c2 + d2) + c2(b2 + c2 + d2)
= (a2 + b2 + c2) (b2 + c2 + d2)
= L.H.S
L.H.S. = R.H.S
(a2 + b2 + c2) (b2 + c2 + d2) = (ab + bc + cd)2