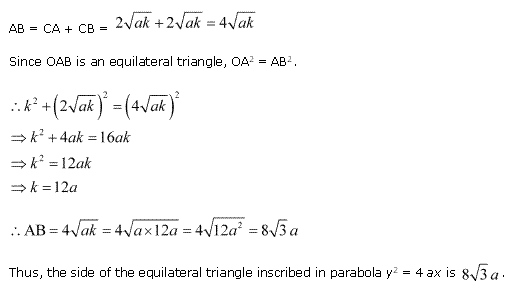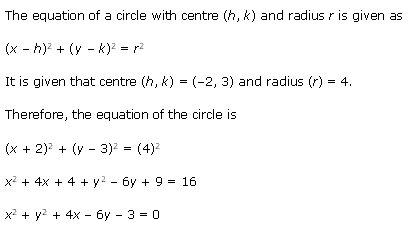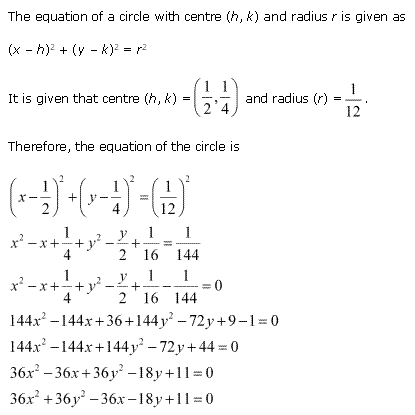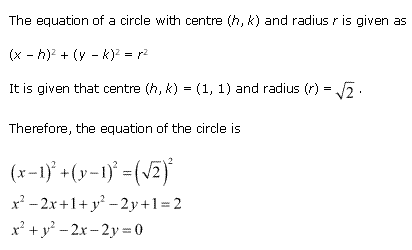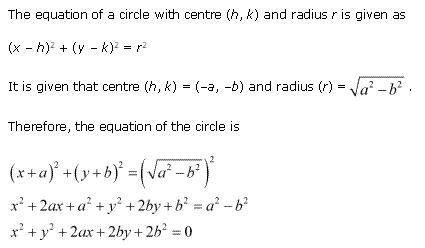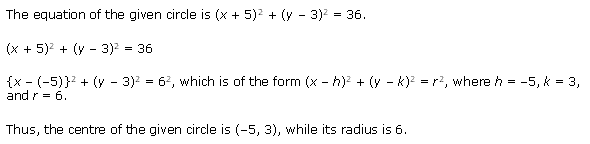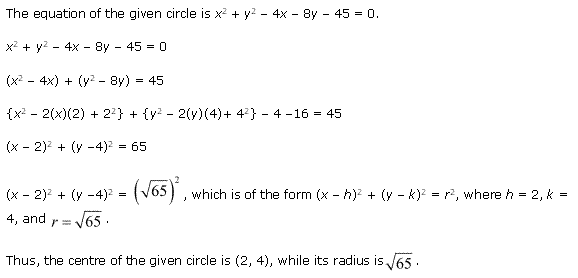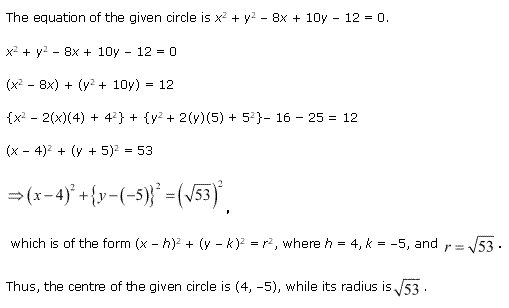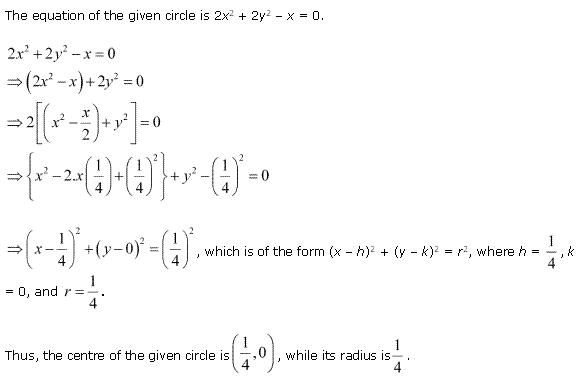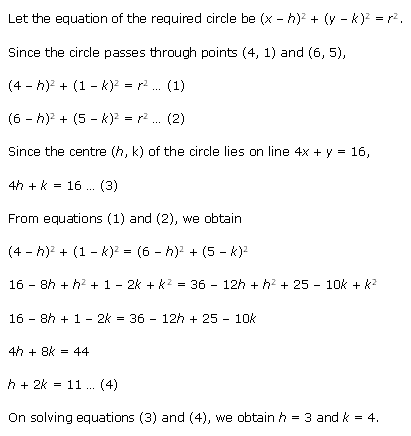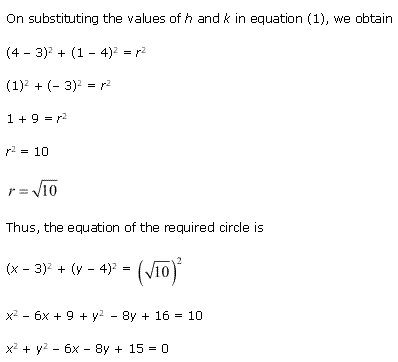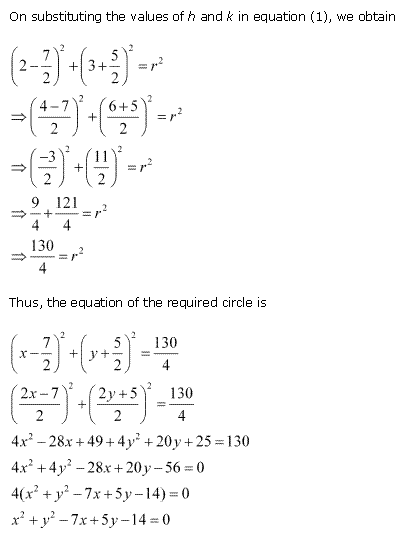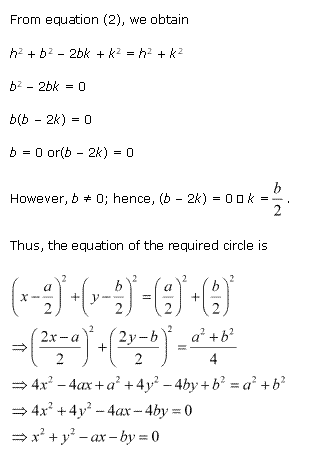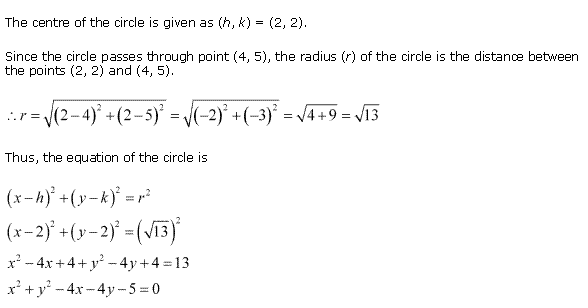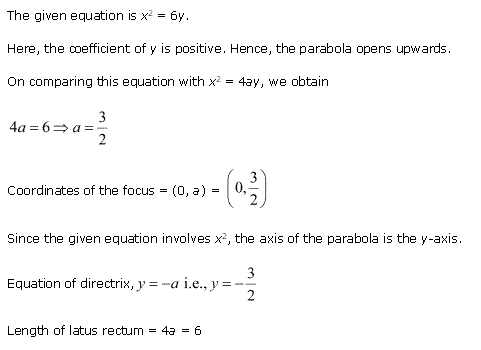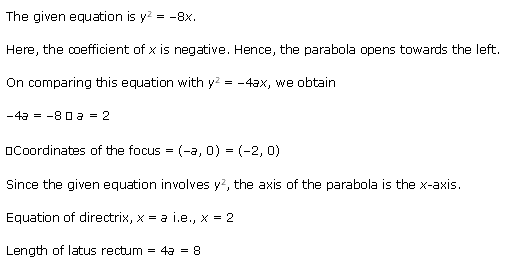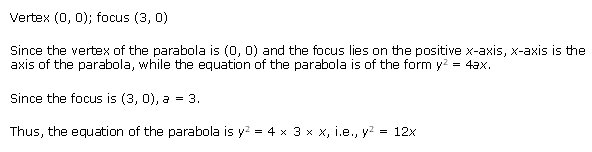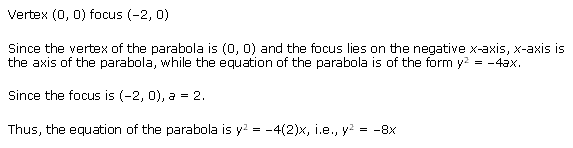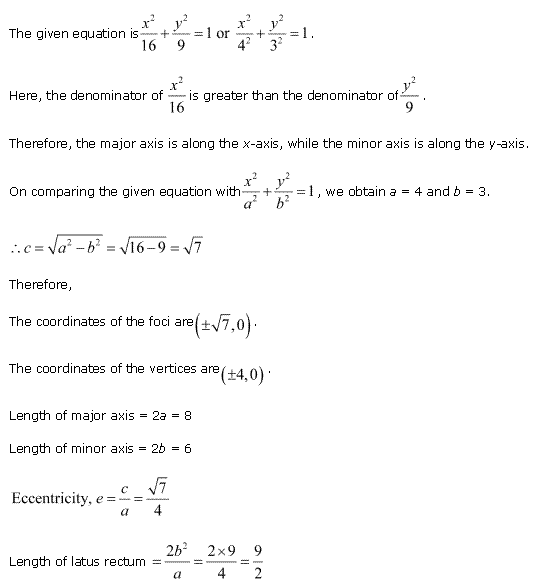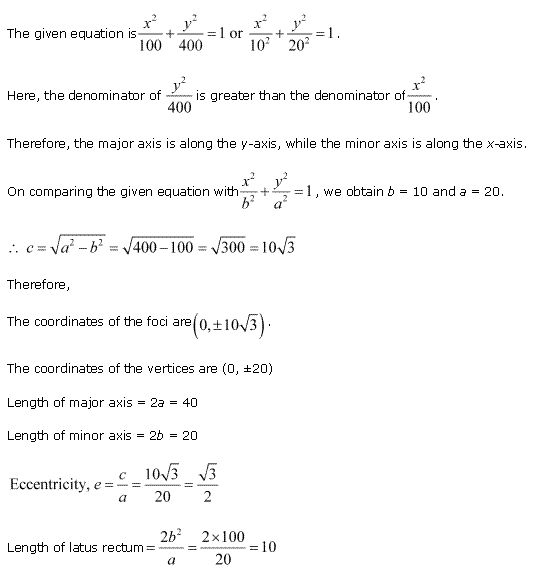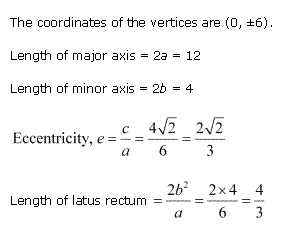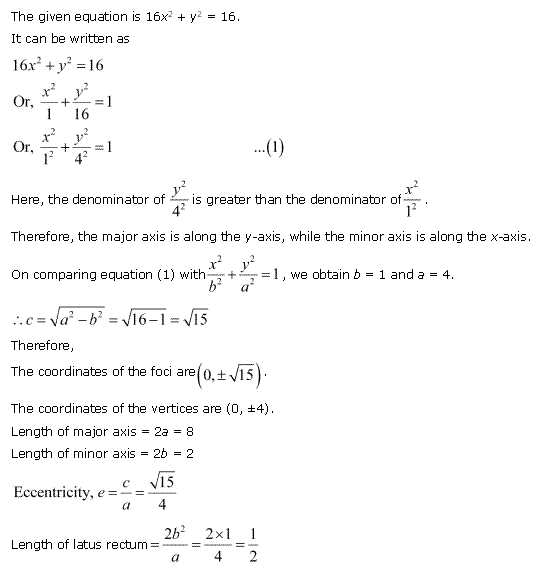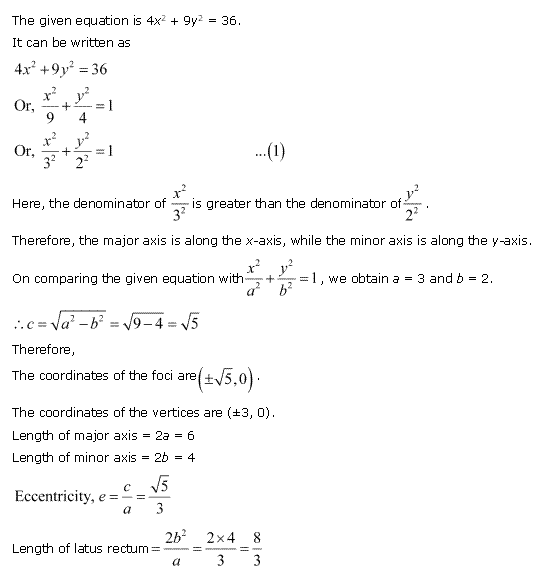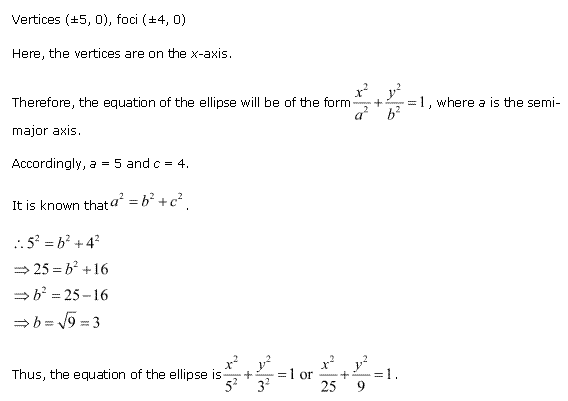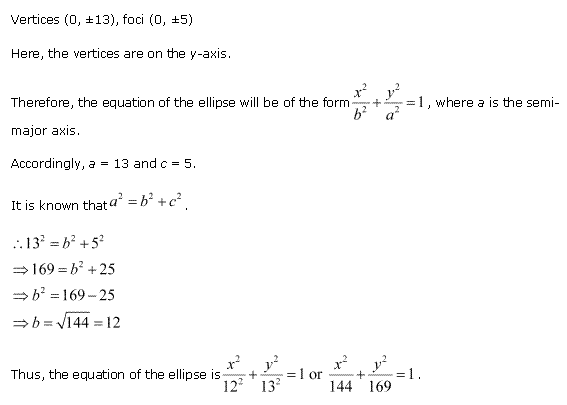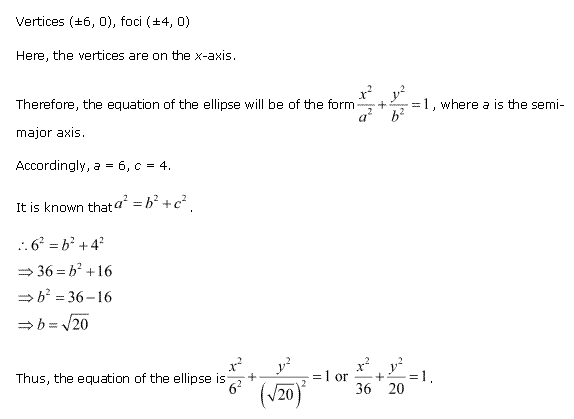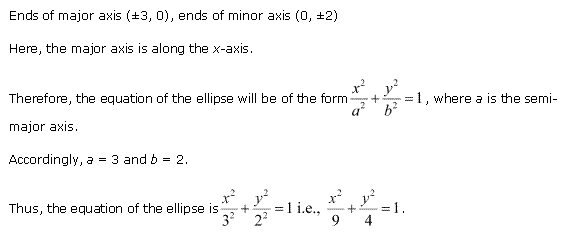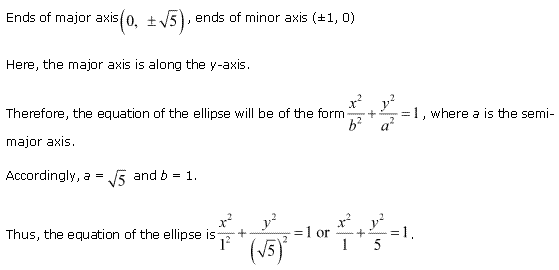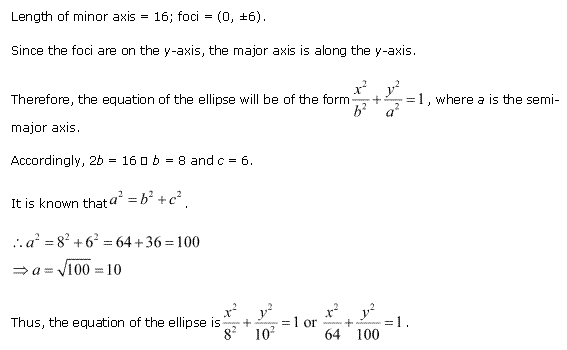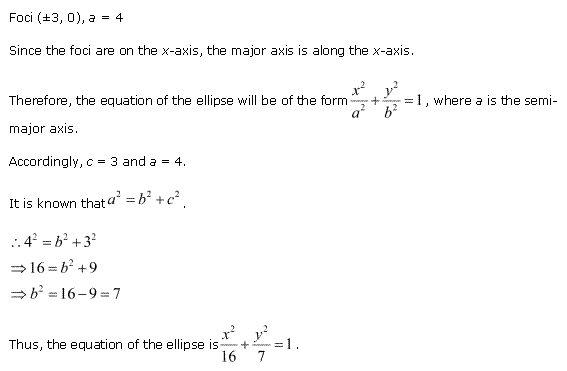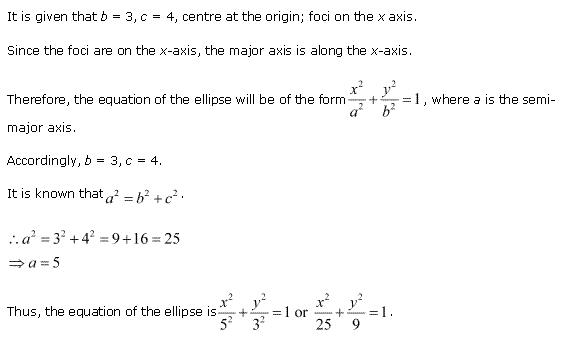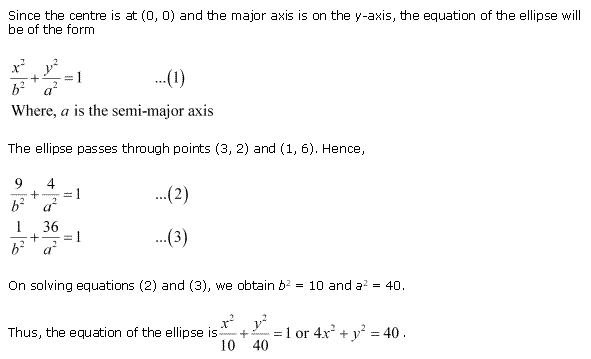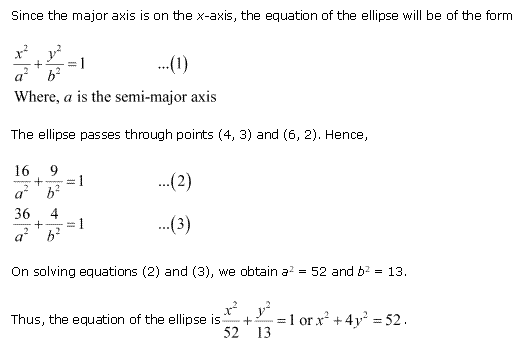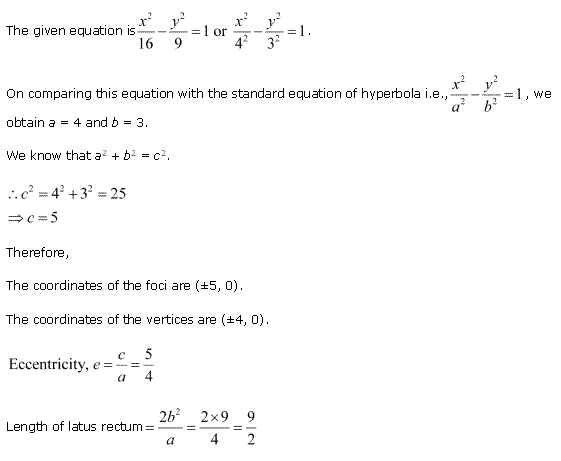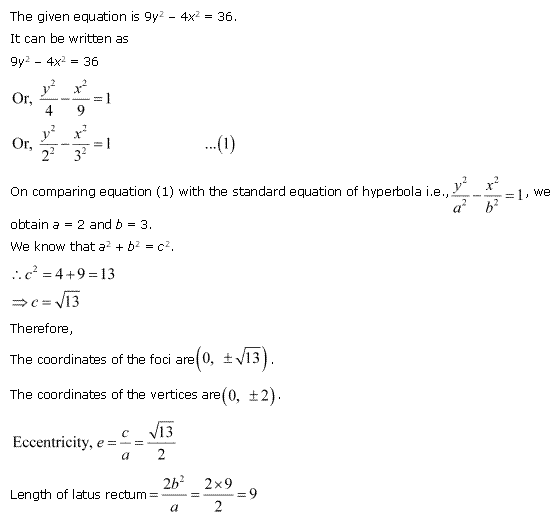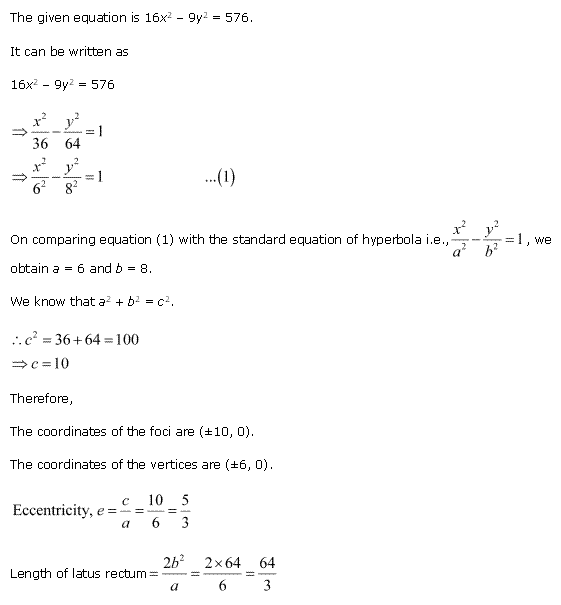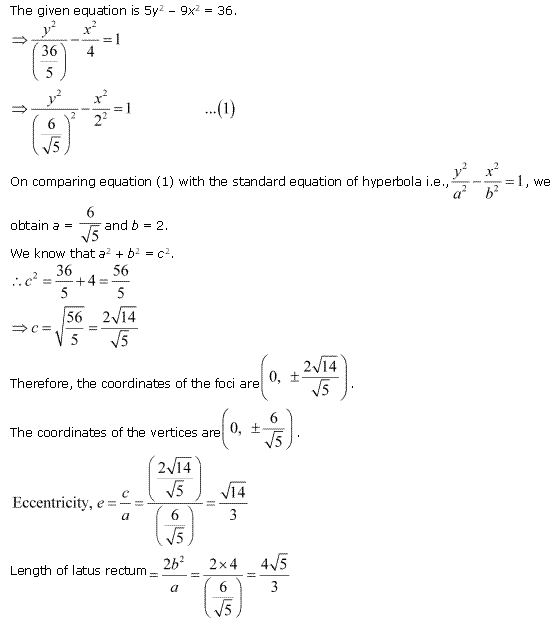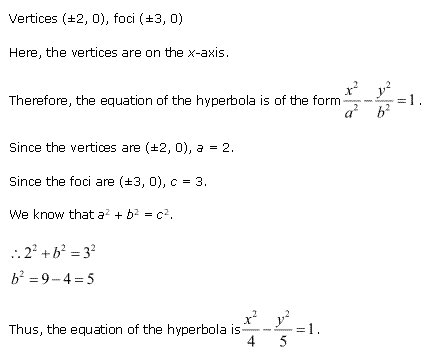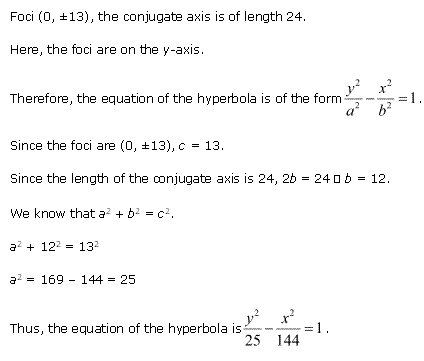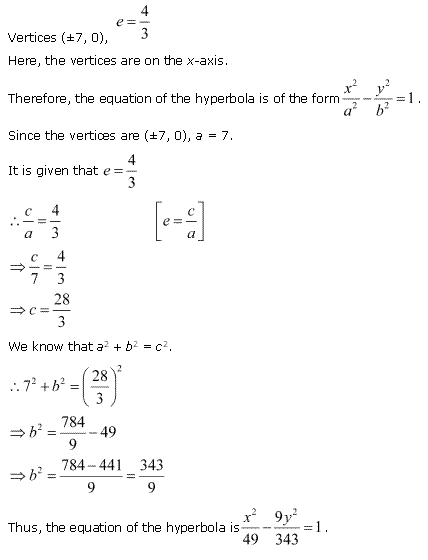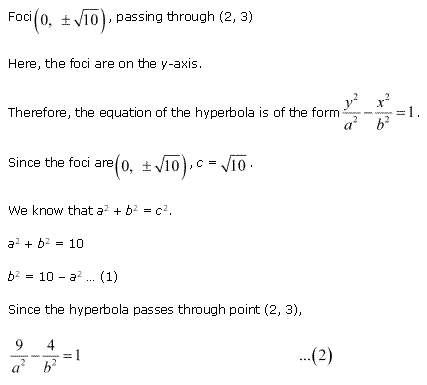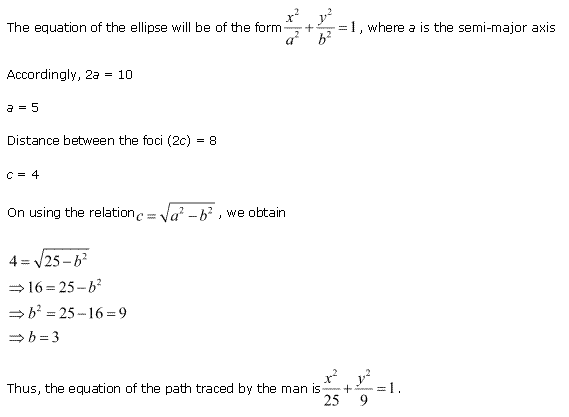Class 11-commerce NCERT Solutions Maths Chapter 10: Conic Sections
Conic Sections Exercise Ex. 10.1
Solution 1
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
Solution 13
Solution 14
Solution 15
Conic Sections Exercise Ex. 10.2
Solution 1
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
Conic Sections Exercise Ex. 10.3
Solution 1
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
Solution 13
Solution 14
Solution 15
Solution 16
Solution 17
Solution 18
Solution 19
Solution 20
Conic Sections Exercise Ex. 10.4
Solution 1
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
Vertices (0, ± 3), foci (0, ± 5)
Here, the vertices are on the y-axis.
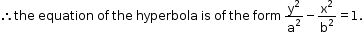
Since the Vertices are (0, ± 3), a = 3
Since the foci are (0, ± 5), c = 5
We know that a2 + b2 = c2
∴ 32 + b2 = 52
∴ b2 = 25 - 9 = 16
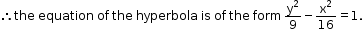
Solution 10
Solution 11
Solution 12
Solution 13
Solution 14
Solution 15
Conic Sections Exercise Misc. Ex.
Solution 1
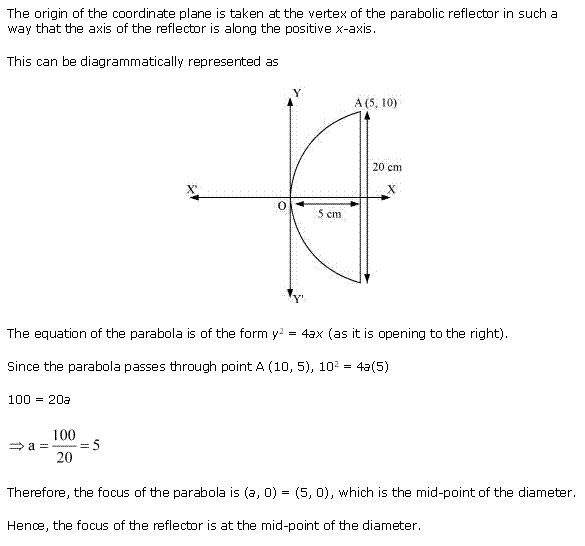
Solution 2
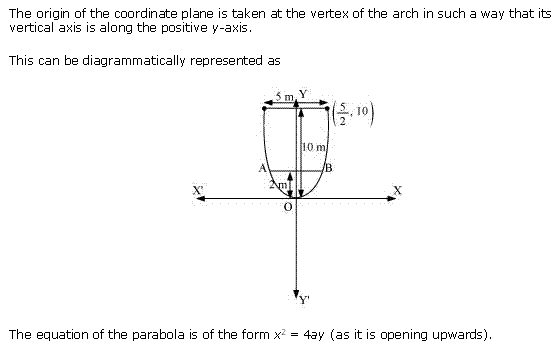

Solution 3
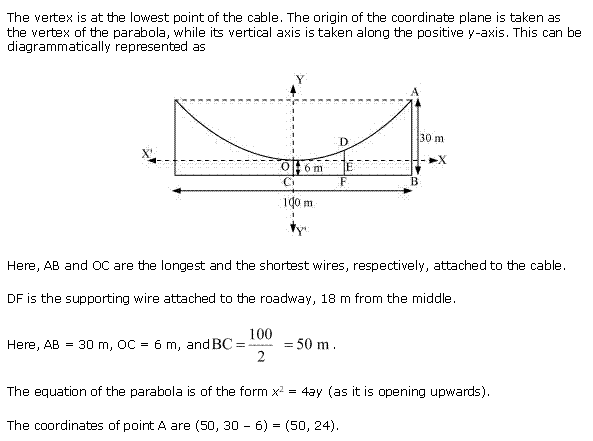

Solution 4
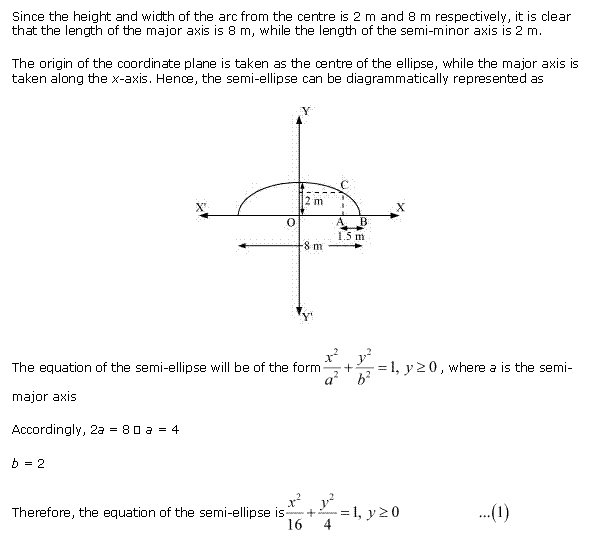

Solution 5
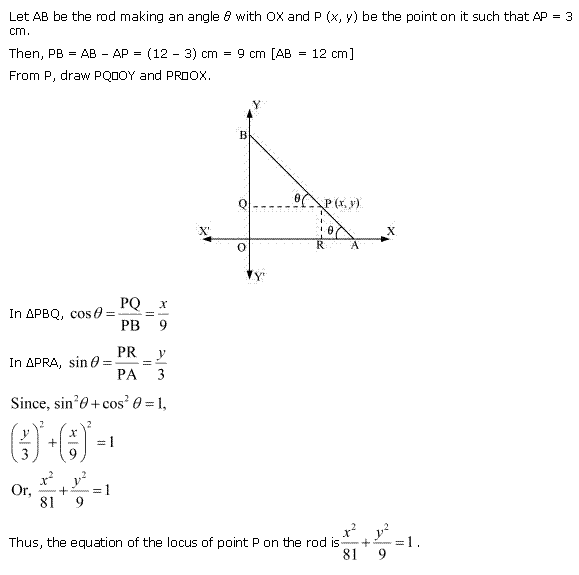
Solution 6

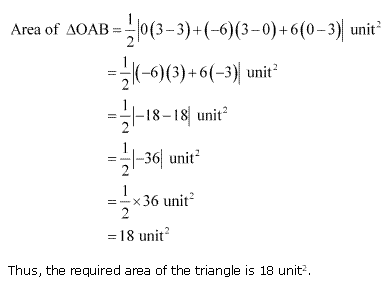
Solution 7
Let A and B the positions of the two flag posts and P(x, y) be the position of the man.
Accordingly, PA + PB = 10
We know that if a point moves in a plane in such a way that the sum of its distances from two fixed points is constant, then the path is an ellipse and this constant value is equal to the length of the major axis of the ellipse.
Therefore, the path described by the man is an ellipse where the length of the major axis is 10 m, while points A and B are the foci.
Taking the origin of the co-ordinate plane as the centre of the ellipse, while taking the major axis along the x-axis, the ellipse can be diagrammatically represented as
Solution 8