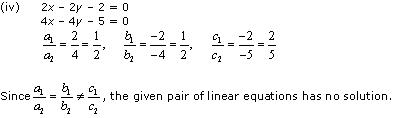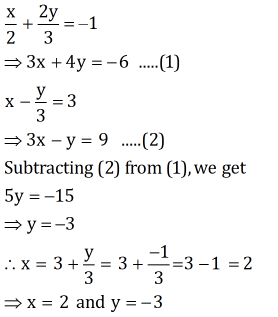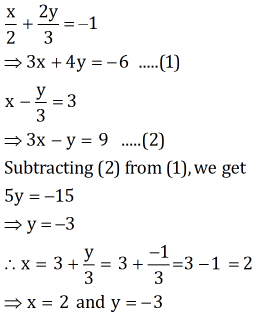Class 10 NCERT Solutions Maths Chapter 3 - Pairs of Linear Equations in Two Variables
Pairs of Linear Equations in Two Variables Exercise Ex. 3.1
Solution 1
(i) Let the number of girls and boys in the class be x and y respectively.
According to the given conditions, we have:
x + y = 10
x - y = 4
x + y = 10 ![]() x = 10 - y
x = 10 - y
Three solutions of this equation can be written in a table as follows:
| x | 5 | 4 | 6 |
| y | 5 | 6 | 4 |
x - y = 4  x = 4 + y
x = 4 + y
Three solutions of this equation can be written in a table as follows:
| x | 5 | 4 | 3 |
| y | 1 | 0 | -1 |
The graphical representation is as follows: 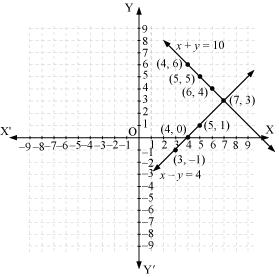
From the graph, it can be observed that the two lines intersect each other at the point (7, 3).
So, x = 7 and y = 3.
Thus, the number of girls and boys in the class are 7 and 3 respectively.
(ii) Let the cost of one pencil and one pen be Rs x and Rs y respectively.
According to the given conditions, we have:
5x + 7y = 50
7x + 5y = 46
Three solutions of this equation can be written in a table as follows:
| x | 3 | 10 | -4 |
| y | 5 | 0 | 10 |
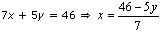
Three solutions of this equation can be written in a table as follows:
| x | 8 | 3 | -2 |
| y | -2 | 5 | 12 |
The graphical representation is as follows: 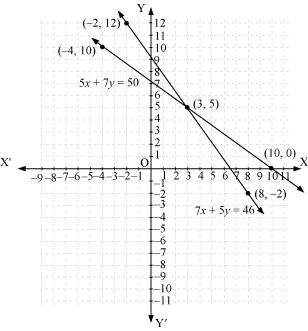
From the graph, it can be observed that the two lines intersect each other at the point (3, 5).
So, x = 3 and y = 5.
Therefore, the cost of one pencil and one pen are Rs 3 and Rs 5 respectively.
Concept insight: Read the question carefully and examine what are the unknowns. Represent the given conditions with the help of equations by taking the unknowns quantities as variables. Also carefully state the variables as whole solution is based on it. On the graph paper, mark the points accurately and neatly using a sharp pencil. Also, take at least three points satisfying the two equations in order to obtain the correct straight line of the equation. Since joining any two points gives a straight line and if one of the points is computed incorrect will give a wrong line and taking third point will give a correct line. The point where the two straight lines will intersect will give the values of the two variables, i.e., the solution of the two linear equations. State the solution point.
Solution 2
(i) 5x - 4y + 8 = 0
7x + 6y - 9 = 0
Comparing these equations with a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, we get: 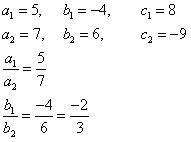
Since , the given pair of equations intersect at exactly one point.
(ii) 9x + 3y + 12 = 0
18x + 6y + 24 = 0
Comparing these equations with a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, we get: 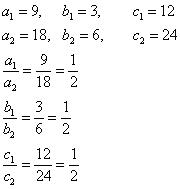
Since , the given pair of equation are coincident.
(iii) 6x - 3y + 10 = 0 , 2x - y + 9 = 0
Comparing these equations with a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, we get: 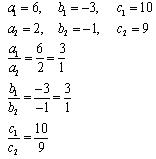
Since , the given pair of equation are parallel to each other.
Concept insight: In order to answer such questions, remember the condition for the pair of linear equations to be intersecting, parallel or coincident. Also, while writing the coefficients, don't forget to take the signs.
Solution 3

Since , the given pair of equation has only one solution.
Thus, the pair of linear equations is consistent. 
Thus, the pair of linear equations is inconsistent. 
Thus, the pair of linear equations is consistent. 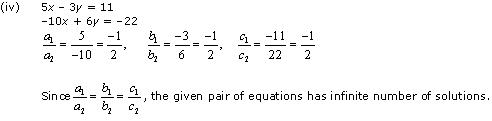
Thus, the pair of linear equations is consistent. 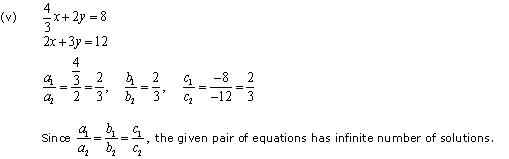
Thus, the pair of linear equations is consistent.
Concept Insight: If a pair of linear equations has one or more than one solution then they are said to be consistent and if they have no solution then they are said to be inconsistent. So, to identify the consistency of a given pair of equations, apply the conditions involving the coefficients of the given pair of equations.
In case, two consistent linear equations are plotted, they will either intersect or overlap each other.
Solution 4
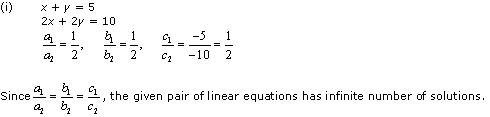
Thus, the pair of linear equations is consistent.
Now, x + y = 5 ![]() x = 5 - y
x = 5 - y
Three solutions of this equation can be written in a table as follows:
| x | 4 | 3 | 2 |
| y | 1 | 2 | 3 |
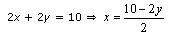
Three solutions of this equation can be written in a table as follows:
| x | 4 | 3 | 2 |
| y | 1 | 2 | 3 |
Thus, the graphical representation is as follows: 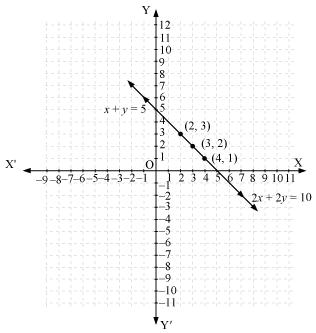
From the graph, it can be observed that the two lines coincide. Thus, the given pair of equations has infinite solutions.
Let x = k, then y = 5 - k. So, the ordered pair (k, 5 - k) , where k is a constant, will be the solution of the given pair of linear equations. 
Thus, the pair of linear equations is inconsistent. 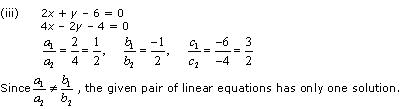
Thus, the pair of linear equations is consistent.
Now, 2x + y - 6 = 0 ![]() y = 6 - 2x
y = 6 - 2x
Three solutions of this equation can be written in a table as follows:
| x | 0 | 1 | 2 |
| y | 6 | 4 | 2 |
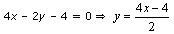
Three solutions of this equation can be written in a table as follows:
| x | 1 | 2 | 3 |
| y | 0 | 2 | 4 |
Thus, the graphical representation is as follows: 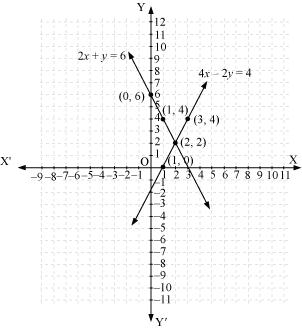
From the graph, it can be observed that the two lines intersect each other at the point (2, 2). Thus, the solution of the given pair of equations is (2, 2).
Thus, the pair of linear equations is inconsistent.
Concept insight: If a pair of linear equations has one or more than one solutions then they are said to be consistent and if they have no solution then they are said to be inconsistent. The graph of each equation can be plotted by taking at least three ordered pairs which are the solutions of the equations. The point where both the lines intersect will be the solution of the given pair of equations. Remember two overlapping lines intersect each other at infinitely many points. State the solution explicitly.
Solution 5
Let the width and length of the rectangular garden be x and y respectively.
According to the given conditions,
y - x = 4
y + x = 36
y - x = 4 ![]() y = x + 4
y = x + 4
Three solutions of this equation can be written in a table as follows:
| x | 0 | 8 | 12 |
| y | 4 | 12 | 16 |
y + x = 36
Three solutions of this equation can be written in a table as follows:
| x | 0 | 36 | 16 |
| y | 36 | 0 | 20 |
Thus, the graphical representation is as follows: 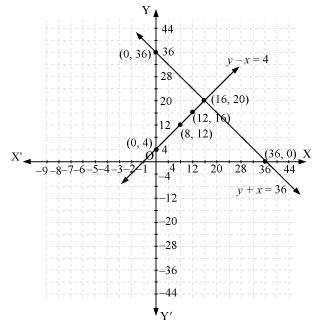
From the graph, it can be observed that the two lines intersect each other at the point (16, 20). So, x = 16 and y = 20.
Thus, the length and width of the rectangular garden is 20 m and 16 m respectively.
Concept insight: Here dimensions of the rectangular garden needs to be found. Since opposite sides of the rectangle are equal so length and breadth can be taken as variables. Applying conditions given in the problem two linear equations in the 2 variables can be obtained. Now, in order to represent the obtained equations graphically, take the values of variables as whole numbers only, because then it will be easier to represent the values on the graph. The point where the two equations intersect will give the required dimensions. State the dimensions length and breadth from the values of the variables.
Solution 6
(i) For the two lines a1x + b1x + c1 = 0 and a2x + b2x + c2 = 0, to be intersecting, we must have 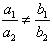
So, the other linear equation can be 5x + 6y - 16 = 0
(ii) For the two lines a1x + b1x + c1 = 0 and a2x + b2x + c2 = 0, to be parallel, we must have 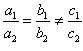
So, the other linear equation can be 6x + 9y + 24 = 0, 
(iii) For the two lines a1x + b1x + c1 = 0 and a2x + b2x + c2 = 0 to be coincident, we must have 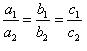
So, the other linear equation can be 8x + 12y - 32 = 0, 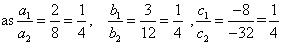
Concept insight: In order to answer such type of problems, just remember the conditions for two lines to be intersecting, parallel, and coincident. This problem will have multiple answers as their can be many equations satisfying the required conditions.
Solution 7
x - y + 1 = 0 ![]() x = y - 1
x = y - 1
Three solutions of this equation can be written in a table as follows:
| x | 0 | 1 | 2 |
| y | 1 | 2 | 3 |
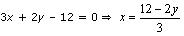
Three solutions of this equation can be written in a table as follows:
| x | 4 | 2 | 0 |
| y | 0 | 3 | 6 |
Now, these equations can be drawn on a graph. The triangle formed by the two lines and the x-axis can be shown by the shaded part as: 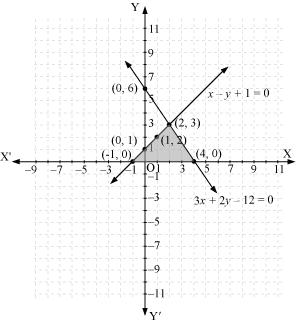
From the graph, it can be observed that the coordinates of the vertices of the triangle so formed are (2, 3), (-1, 0), and (4, 0).
Concept insight: In order to find the coordinates of the vertices of the triangle so formed, find the points where the two lines intersects the x-axis and also where the two lines intersect each other. Note here that the coordinates of the intersection of lines with x-axis is taken and not with y-axis, this is because the question says to find the triangle formed by the two lines and the x-axis.
Pairs of Linear Equations in Two Variables Exercise Ex. 3.2
Solution 1
(i) x + y = 14 ... (i)
x - y = 4 ... (ii)
From (i), we obtain:
x = 14 - y ... (iii)
Substituting this value in equation (ii), we obtain: 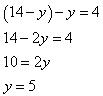
Substituting the value of y in equation (iii), we obtain:
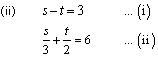
From (i), we obtain:
s = t + 3 ...(iii)
Substituting this value in equation (ii), we obtain:
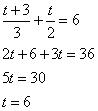
Substituting the value of t in equation (iii), we obtain:
s = 9
(iii) 3x - y = 3 ... (i)
9x - 3y = 9 ... (ii)
From (i), we obtain
y = 3x - 3 ... (iii)
Substituting this value in equation (ii), we obtain:
9 = 9
This is always true.
Thus, the given pair of equations has infinitely many solutions and the relation between these variables can be given by
y = 3x - 3
So, one of the possible solutions can x = 3, y = 6.

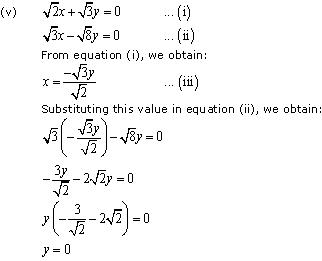
Substituting the value of y in equation (iii), we obtain:
x = 0

Concept insight: In order to solve the given pairs of equations, we need to substitute the value of any one of the variable from any one of the equation. But make sure to substitute the value of that variable which simplifies calculations. For example, in part (iv) it is most convenient to substitute the value of x from the first equation to the second equation, as the division by 0.2 is more easier than the division by 0.3, 0.4 and 0.5.
Solution 2
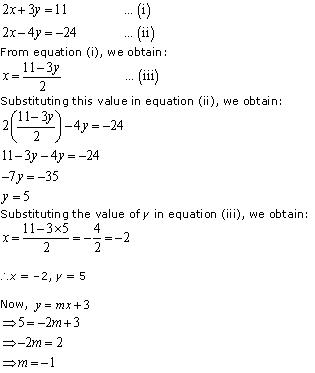
Thus, the value of m is -1.
Concept insight: Firstly the solution of the given pair of linear equations can be found out by substituting the value of one variable, say x, from one equation into the other equation. Then after finding out the values of x and y, substitute them in the equation y = m x + 3 in order to find the value of m.
Solution 3
(i) Let one number be x and the other number be y such that y > x.
According to the question: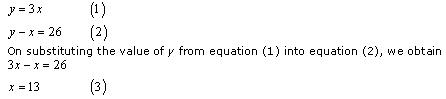
Substituting this in equation (1), we obtain
y = 39
Hence, the numbers are 13 and 39.
Concept insight: In this problem, two relations between two numbers are given. So, the two numbers have to be found out here. So the two numbers will be represented by variables x and y explicitly state the greater variable.
A pair of equations can be obtained from the given conditions. The pair of equations can then be solved by suitable substitution.
(ii) Let the larger angle be x and smaller angle be y.
We know that the sum of the measures of angles of a supplementary pair is always 180º.
According to the given information,
From (1), we obtain
x = 180º - y (3)
Substituting this in equation (2), we obtain 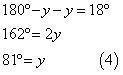
Putting this in equation (3), we obtain
x = 180º - 81º
= 99º
Hence, the angles are 99º and 81º.
Concept insight: This problem talks about the measure of two supplementary angles. So, the two angles will be written as variables. The pair of equations can be formed using the fact that the sum of two supplementary angles is 180° and using the condition given in the problem. The pair of equations can then be solved by suitable substitution.
(iii) Let the cost of a bat and a ball be x and y respectively.
According to the given information, 
Hence, the cost of a bat is Rs 500 and that of a ball is Rs 50.
Concept insight: Cost of bats and balls needs to be found so the cost of a ball and bat will be taken as the variables. Applying the conditions of total cost of bats and balls algebraic equations will be obtained. The pair of equations can then be solved by suitable substitution.
Concept insight: In this problem, we are required to find out the fixed charge and the charge per km. So, we will represent these two by using different variables. Now, two linear equations can be written by using the conditions given in the problem. The pair of equations can then be solved by suitable substitution.
(v) Let the fraction be ![]()
According to the given information, 
Concept insight: This problem talks about a fraction which is not known to us. So numerator and denominators will be taken to be variables x and y respectively and y will be strictly non zero. Then, a pair of linear equations can be formed from the given conditions. The pair of equations can then be solved by suitable substitution.
(vi) Let the age of Jacob be x and the age of his son be y.
According to the given information, 
Hence, the present age of Jacob is 40 years whereas the present age of his son is 10 years.
Concept insight: Here, Jacob's and his son's present age are not known. So, we will write both these in terms of variables. The problem talks about their ages five years ago and five years hence. Here, five years ago means we have to subtract 5 from their present ages, and five years hence means we have to add 3 to their present ages. So, using the given conditions, a pair of linear equations can be formed. The pair of equations can then be solved by suitable substitution.
Pairs of Linear Equations in Two Variables Exercise Ex. 3.3
Solution 1
(ii) Elimination method:
3x + 4y = 10 ...(1)
2x - 2y = 2 ...(2)
Multiplying equation (2) by 2, we obtain:
4x - 4y = 4 ...(3)
Adding equation (1) and (3), we obtain
7x = 14
x = 2
Substituting the value of x in equation (1), we obtain:
6 + 4y = 10
4y = 4
y = 1
Hence, x = 2, y = 1
Substitution method:
From equation (2), we obtain:
x = 1 + y ...(4)
Putting this value in equation (1), we obtain:
3(1 + y) + 4y = 10.
7y = 7
y = 1
Substituting the value of y in equation (4), we obtain:

(iv) Elimination Method:
Substitution method:
From equation (2), we obtain:
y = 3x - 9 ... (3)
Putting this value in equation (1), we obtain:
3x + 4(3x - 9) = -6
15x = 30
x = 2
Substituting the value of x in equation (3), we obtain:
y = 6 - 9 = -3
Concept insight: In order to solve the given pairs of equations by elimination method, it is required to eliminate one variable to get a linear equation in one variable. For elimination, we multiply one equation (or sometimes even both equations) by suitable constant to make the coefficient of one variable same in both the equations. The trick is to eliminate that variable which involves lesser computations.
In order to solve the given pair of equations by substitution method, we need to substitute the value of any one of the variable from any one of the equation. The trick here is to make sure you substitute the value of that variable which simplifies your calculations.
Note that the solution must be same in both the cases.
Solution 2
(i) Let the fraction be
According to the question, 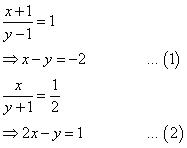
Subtracting equation (1) from equation (2), we obtain:
x = 3
Substituting this value of x in equation (1), we obtain: 
Concept insight: This problem talks about a fraction. The numerator and denominator of the fraction are not known so we represent these as variables x and y respectively where variable y must be non zero. Then, a pair of linear equations can be formed from the given conditions. The pair of equations can then be solved by eliminating a suitable variable.
(ii) Let present age of Nuri and Sonu be x and y respectively.
According to the question, 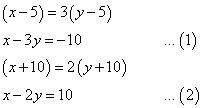
Subtracting equation (1) from equation (2), we obtain:
y = 20
Substituting the value of y in equation (1), we obtain:
Thus, the age of Nuri and Sonu are 50 years and 20 years respectively.
Concept insight: Here, Nuri's and Sonu's present age are not known. So, we will write both these in terms of variables. Then, using the given conditions, a pair of linear equations can be formed. The pair of equations can then be solved by eliminating a suitable variable.
(iii) Let the units digit and tens digit of the number be x and y respectively.
Number = 10y + x
Number after reversing the digits = 10x + y
According to the question,
x + y = 9 ... (1)
9(10y + x) = 2(10x + y)
88y - 11x = 0
- x + 8y =0 ... (2)
Adding equations (1) and (2), we obtain:
9y = 9
y = 1
Substituting the value of y in equation (1), we obtain:
x = 8
Thus, the number is 10y + x = 10 x 1 + 8 = 18
Concept insight: This problem talks about a two digit number. Here, remember that a two digit number xy can be expanded as 10x + y. Then, using the two given conditions, a pair of linear equations can be formed which can be solved by eliminating one of the variables.
(iv) Let the number of Rs 50 notes and Rs 100 notes be x and y respectively.
According to the question, 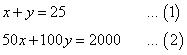
Multiplying equation (1) by 50, we obtain:
50x + 50 y = 1250 .... (3)
Subtracting equation (3) from equation (2), we obtain:
50y = 750
y = 15
Substituting the value of y in equation (1), we obtain:
x = 10
Hence, Meena received 10 notes of Rs 50 and 15 notes of Rs 100.
Concept insight: This problem talks about two types of notes, Rs 50 notes and Rs 100 notes. And the number of both these notes with Meena is not known. So, we denote the number of Rs 50 notes and Rs 100 notes by variables x and y respectively. Now two linear equations can be formed by the given conditions which can be solved by eliminating one of the variables.
(v) Let the fixed charge for first three days and each day charge thereafter be Rs x and Rs y respectively.
According to the question, 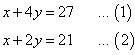
Subtracting equation (2) from equation (1), we obtain:
2y = 6
y = 3
Substituting the value of y in equation (1), we obtain:
x + 12 = 27
x = 15
Hence, the fixed charge is Rs 15 and the charge per day is Rs 3.
Concept insight: Here, the fixed charges for the first three days and per day charges are not known so, they will be represented using two different variables. The two equations can then be obtained by using the given conditions which can be solved by eliminating one of the variables.