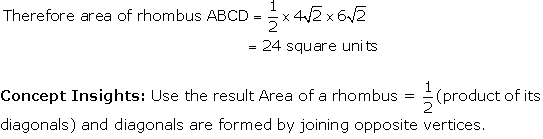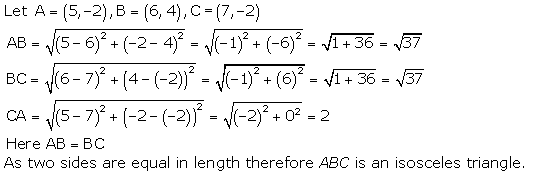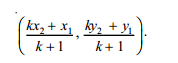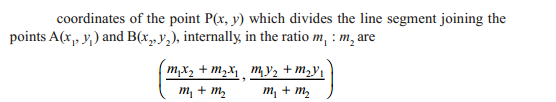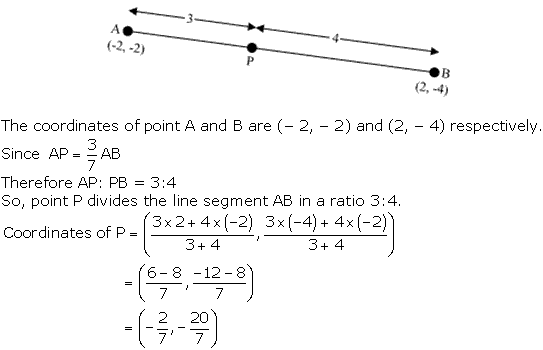Class 10 NCERT Solutions Maths Chapter 7 - Coordinate Geometry
Coordinate Geometry Exercise Ex. 7.1
Solution 1

Solution 2
In section 7.2, A is (4,0) and B is (6,0).
AB2 = (6 - 4)2 - (0 - 0)2 = 4
AB = 2
Solution 3
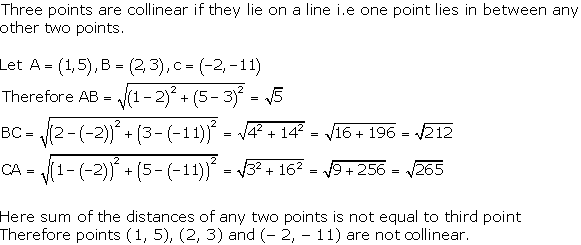
Solution 4
Three non collinear points will represent the vertices of an isosceles triangle, if its two sides are of equal length.
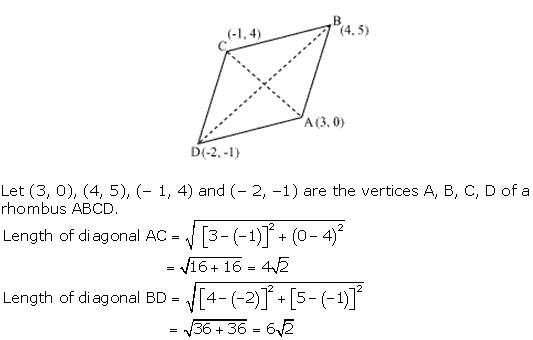
Solution 5
From the figure coordinates of points A, B, C and D are
A = (3, 4), B = (6, 7), C = (9, 4), D = (6, 1)
Solution 6
Here all sides of this quadrilateral are of different length. So, we can say that it is only a general quadrilateral not specific like square, rectangle etc.
(iii) Let A = (4, 5), B = (7, 6), C = (4, 3), D = (1, 2)
Here opposite sides of this quadrilateral are of same length but diagonals are of different length. So, given points are vertices of a parallelogram.
Concept Insight: Recall the properties of various quadrilaterals.
Solution 7
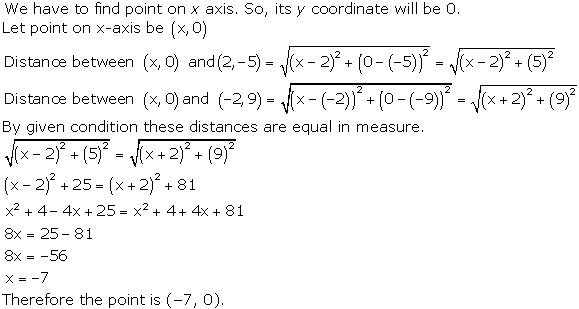
Solution 8
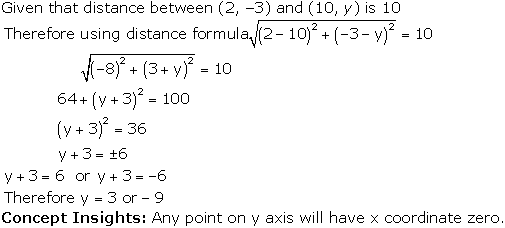
Solution 9
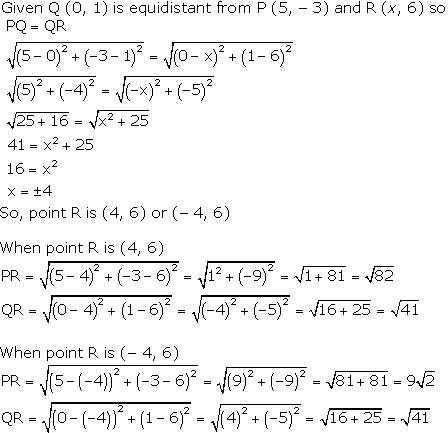
Solution 10

Coordinate Geometry Exercise Ex. 7.2
Solution 1
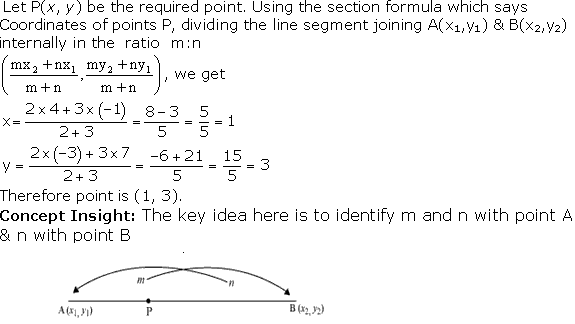
Solution 2


Solution 3

Solution 4

Solution 5
If the ratio in which P divides AB is k:1 , then the co-ordinates of the point P will be
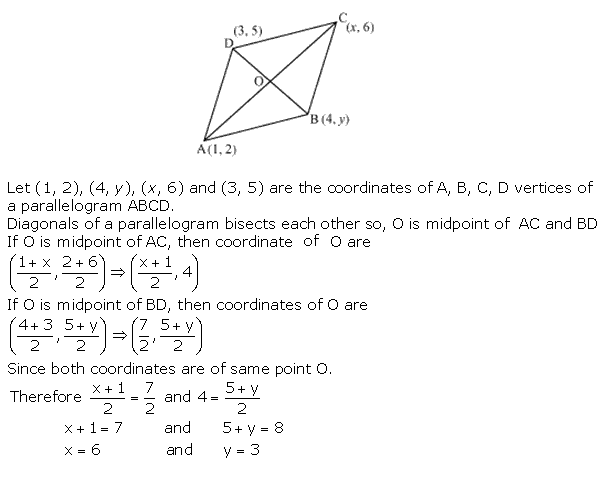
Solution 6
Concept Insight:
Use the property of a parallelogram that the diagonals of a Parallelogram bisects each other for finding the values of a and y.
Solution 7
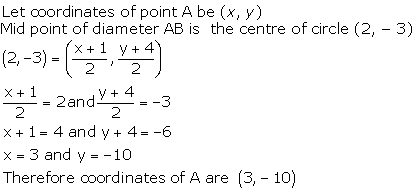
Solution 8
Solution 9
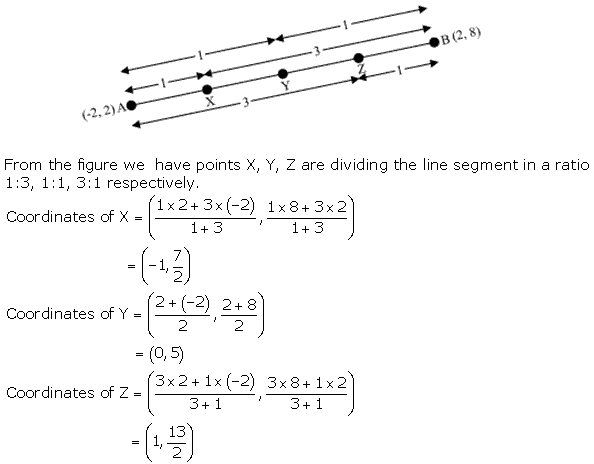
Solution 10