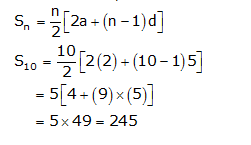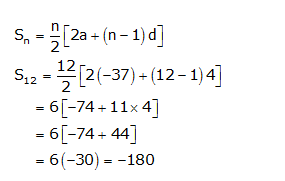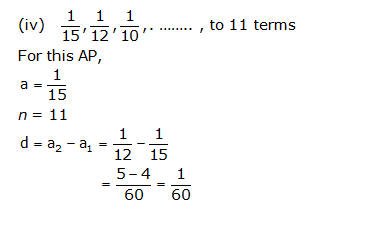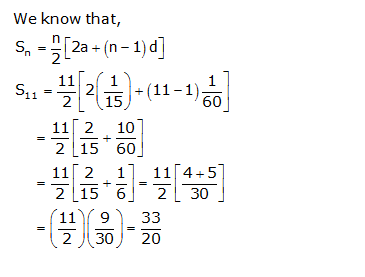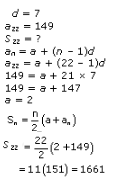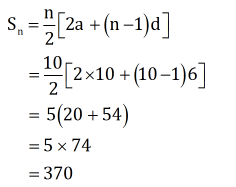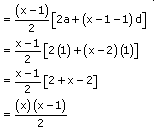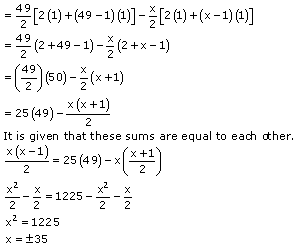Class 10 NCERT Solutions Maths Chapter 5 - Arithmetic Progressions
Arithmetic Progressions Exercise Ex. 5.1
Solution 1
Solution 2
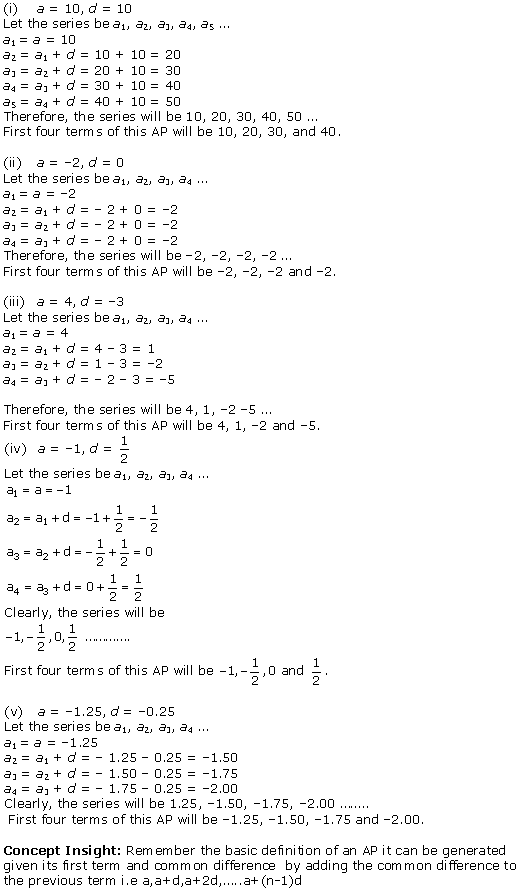
Solution 3

Solution 4
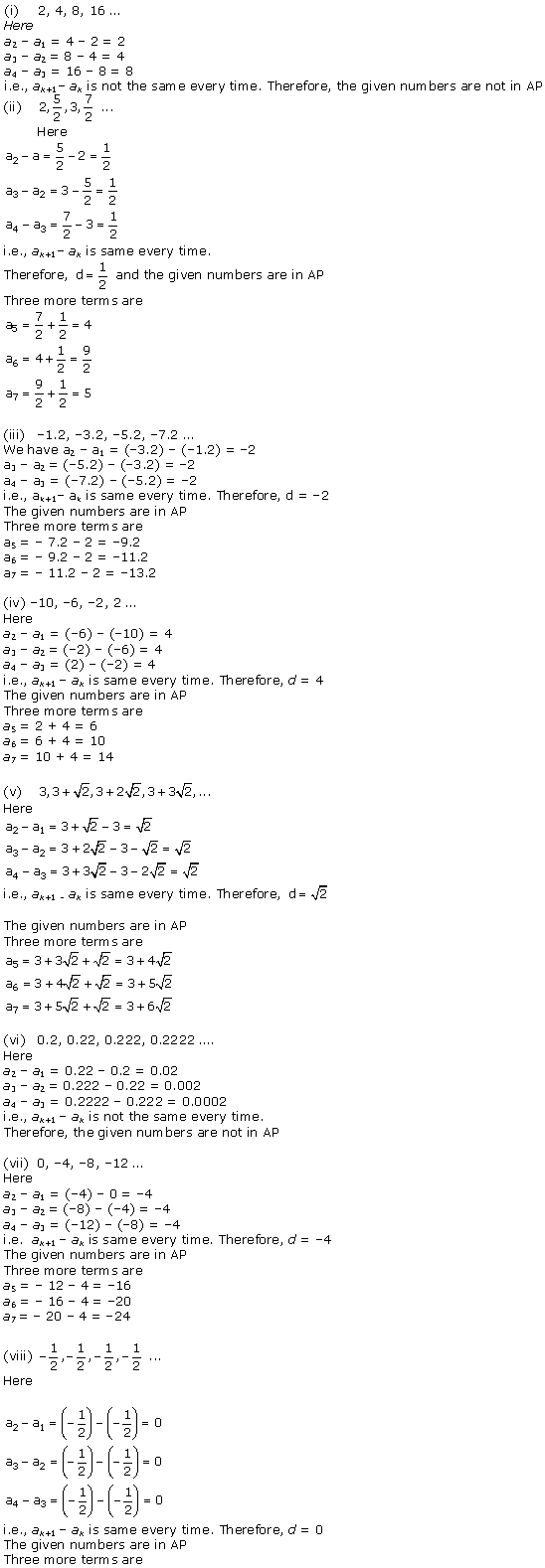
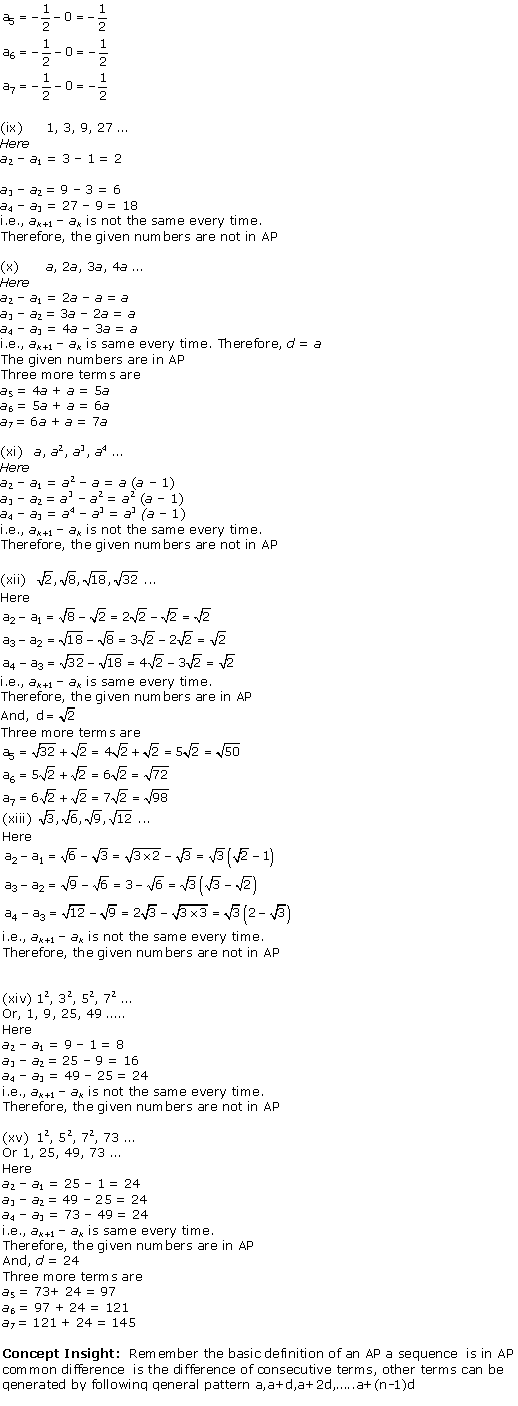
Arithmetic Progressions Exercise Ex. 5.2
Solution 1
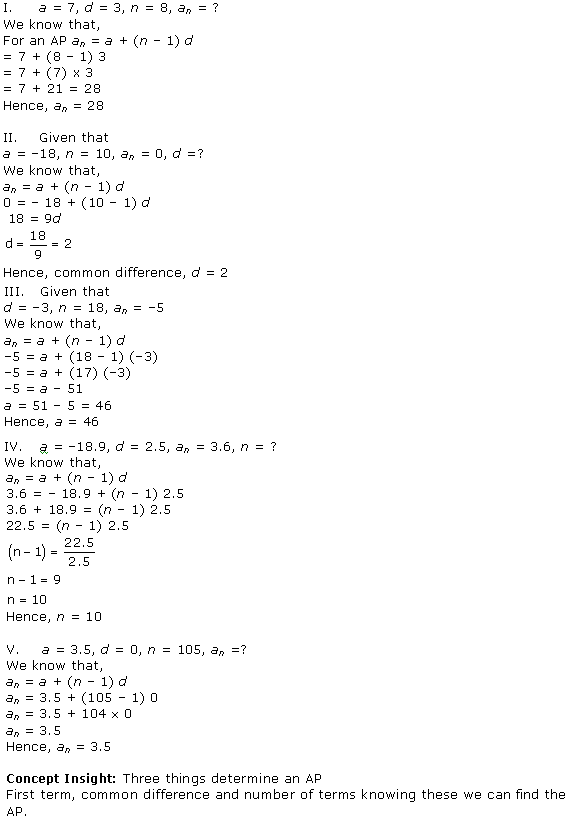
Solution 2
We have to find the 30th term and 11th term in I and II respectively.
Solution 3
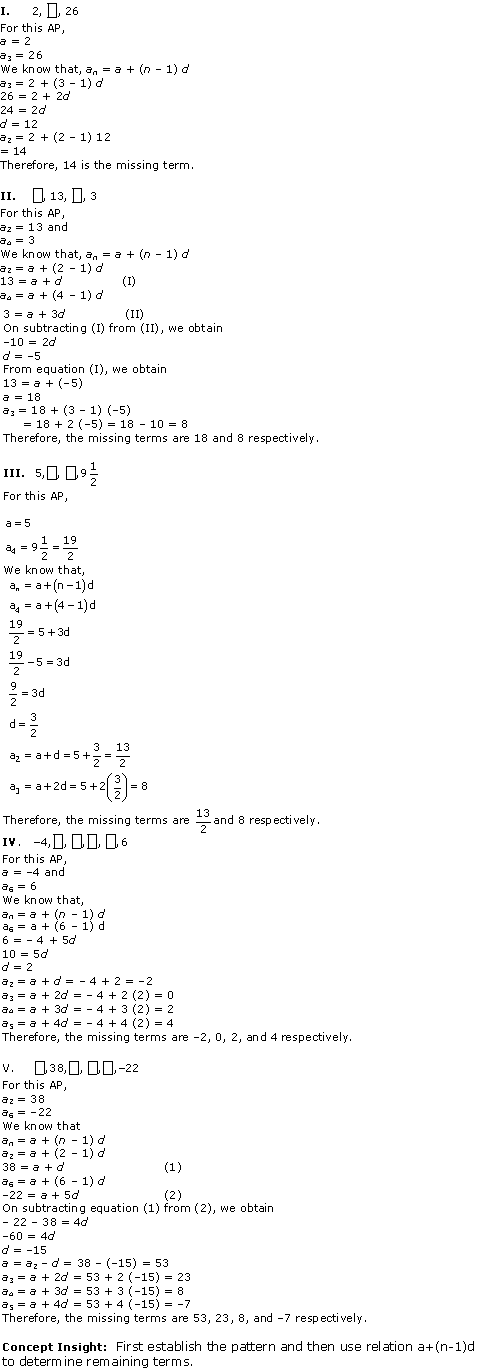
Solution 4

Solution 5
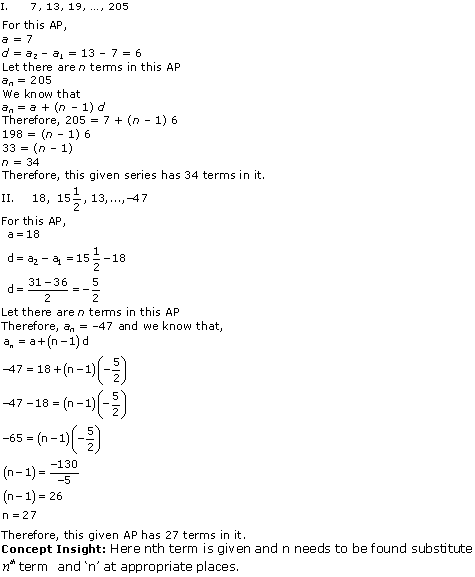
Solution 6

Solution 7

Solution 8

Solution 9

Solution 10
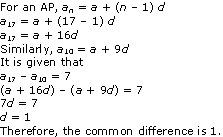
Solution 11

Solution 12

Solution 13

Solution 14

Solution 15
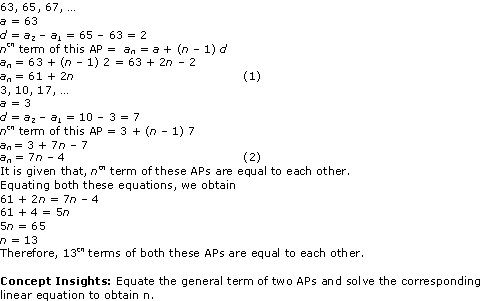
Solution 16
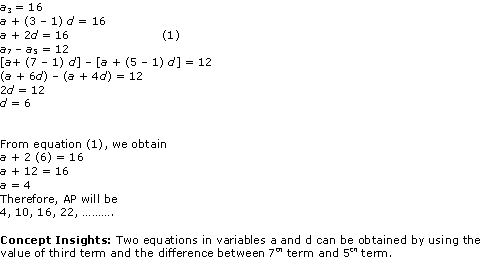
Solution 17
Solution 18
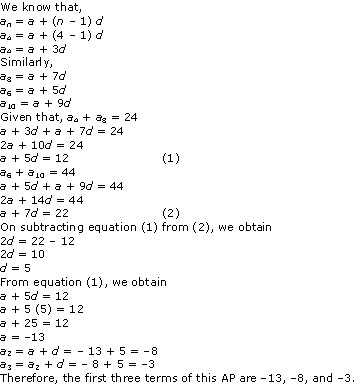
Solution 19

Solution 20

Arithmetic Progressions Exercise Ex. 5.3
Solution 1
(i) 2, 7, 12 ,…, to 10 terms
For this AP,
a = 2
d = a2 – a1 = 7 – 2 = 5
n = 10
We know that,
(ii) –37, –33, –29 ,…, to 12 terms
For this AP,
a = –37
d = a2 – a1 = (–33) – (–37)
= – 33 + 37 = 4
n = 12
We know that,
(iii) 0.6, 1.7, 2.8 ,…, to 100 terms
For this AP,
a = 0.6
d = a2 – a1 = 1.7 – 0.6 = 1.1
n = 100
We know that,
Solution 2
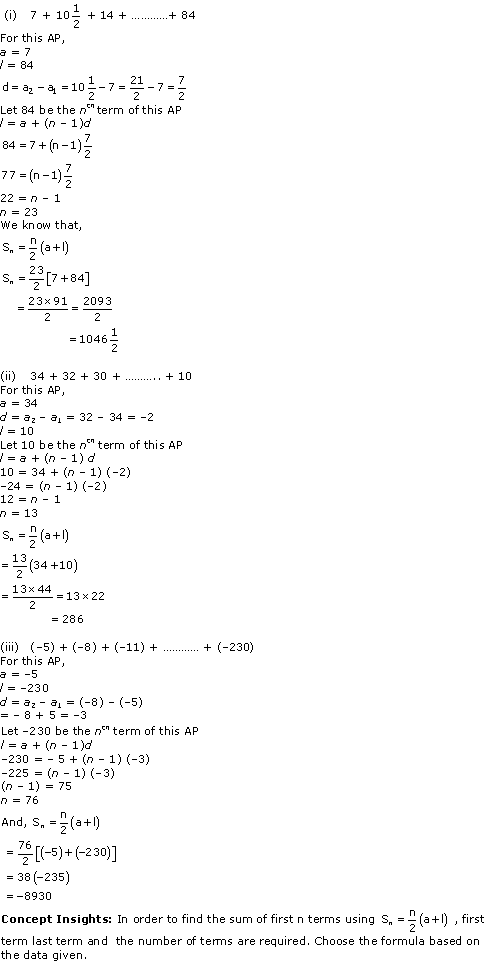
Solution 3
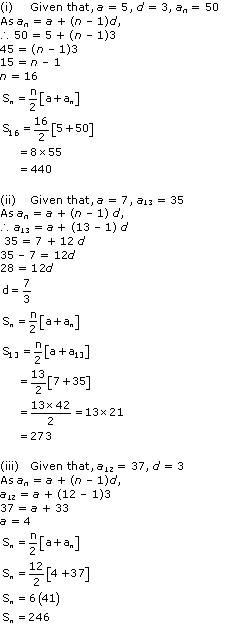
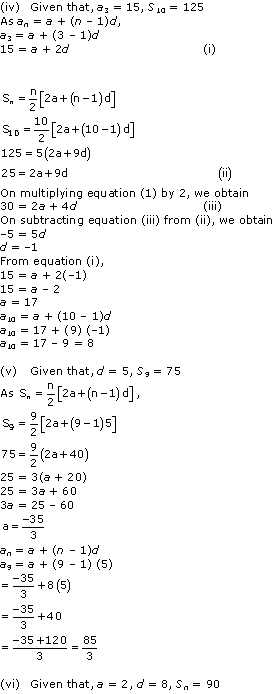
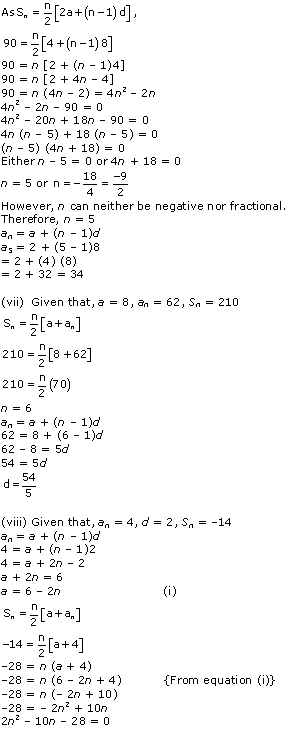

Solution 4

Solution 5

Solution 6

Solution 7
Solution 8
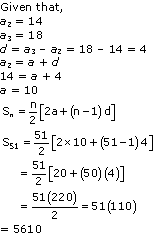
Solution 9

Solution 10
(i)
(ii)
Solution 11

Solution 12

Solution 13

Solution 14
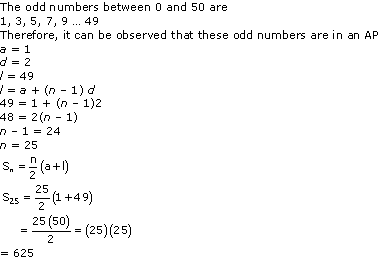
Solution 15

Solution 16

Solution 17

Solution 18
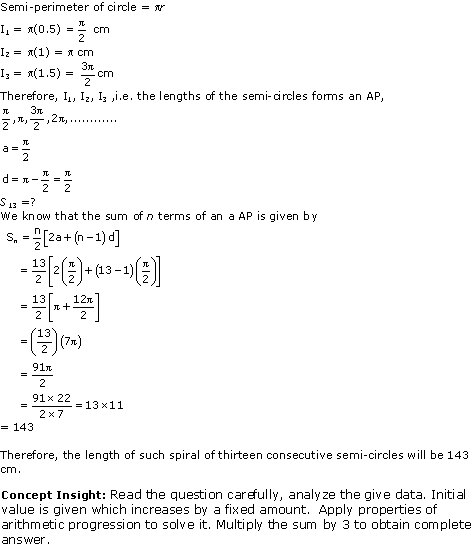
Solution 19

Solution 20
In a potato race, a bucket is placed at the starting point, which is 5m from the first potato and other potatoes are placed 3m apart in a straight line. There are ten potatoes in the line.
So, we get the series as
5, 8, 11, 14, ........
Here, a= 5 and d = 8 - 5 = 11 - 8= 3
the difference between the two consecutive terms are same.
So, this is an arithmetic Progression.
According to the condition, we get the series as
5 + 5 , 8 + 8, 11 + 11, .....
10, 16, 22, ..............
Here a = 10 and d = 16 - 10 = 6
the difference between the two consecutive terms are same.
So, this is an arithmetic Progression.
The total distance the competitor has to run is given by,
Therefore the total distance the competitor has to run is 370 m.
Arithmetic Progressions Exercise Ex. 5.4
Solution 1

Solution 2
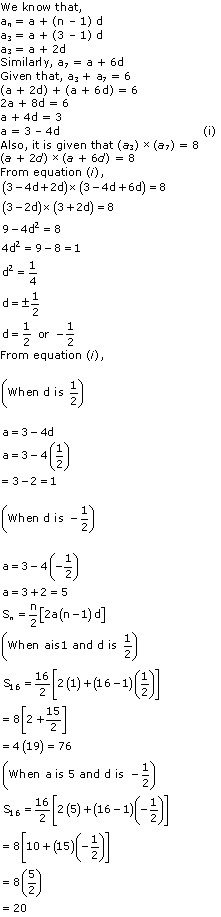
Solution 3
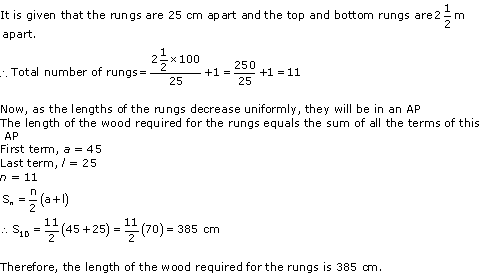
Solution 4
The number of houses was 1, 2, 3, ..... 49.
It can be observed that the number of houses are in an AP having a as 1 and d also as 1.
Let us assume that the number of xth house was like this.
We know that,
![]()
Sum of number of houses preceding xth house = Sx-1
Sum of number of houses preceding xth house = S49 - Sx
However, the house numbers are positive integers.
The value of x will be 35 only.
Therefore, house number 35 is such that the sum of the numbers of houses preceding
the house numbered 35 is equal to the sum of the numbers of the houses following it.
Solution 5