Class 9 MAHARASHTRA STATE TEXTBOOK BUREAU Solutions Maths Chapter 3 - Triangles

Given: ∠A = 70° , ∠B = 40°

Since, ∠ACD is an exterior angle of ∆ABC.

∴ ∠ACD = ∠A + ∠B

= 70° + 40°

∴ ∠ACD = 110°

Given: ∠P = 70°, ∠Q = 65°

We know that, sum of the measures of the angles of a triangle is 180°.

∴ In ∆PQR,

∠P + ∠Q + ∠R = 180°

∴ 70° + 65° + ∠R = 180°

∴ ∠R = 180° - 70° - 65°

∴ ∠R = 45°

It is given that the measures of the angles of a triangle are x°, (x - 20)°, (x - 40)°.

∴ x° + (x - 20)° + (x - 40)° = 180°

… [Since, sum of the measures of the angles of a triangle is 180°]

∴ 3x - 60 = 180

∴ 3x = 180 + 60

∴ 3x = 240

∴ x = 240

∴ x = 80

∴ The measures of the remaining angles are

(x - 20)° = 80° - 20° = 60°,

(x - 40)° = 80° - 40° = 40°

∴ The measures of the angles of the triangle are 80°, 60° and 40°.

Let the measure of the smallest angle be x°.

One of the angles is twice the measure of the smallest angle.

∴ Measure of that angle = 2x°

Another angle is thrice the measure of the smallest angle.

∴ Measure of that angle = 3x°

∴ The measures of the remaining two angles are 2x° and 3x°.

Since, sum of the measures of the angles of a triangle is 180°.

∴ x° + 2x° + 3x° = 180°

∴ 6x = 180

∴ x = 30

∴ x° = 30°

The measures of the remaining angles are

2x° = 2 × 30° = 60°

3x° = 3 × 30° = 90°

The measures of the three angles of the triangle are 30°, 60° and 90°.

Given: ∠NET = 100° and ∠EMR = 140°

∠EMN + ∠EMR = 180° … [Angles in a linear pair]

∴ z + 140° = 180°

∴ z = 180° - 140°

∴ z = 40°

Also, ∠NET + ∠NEM = 180° … [Angles in a linear pair]

∴ 100° + y = 180°

∴ y = 180° - 100°

∴ y = 80°

In ∆ENM,

∴ ∠ENM + ∠NEM + ∠EMN = 180°

… [Sum of the measures of the angles of a triangle is 180°]

∴ x + 80° + 40° = 180°

∴ x = 180° - 80° - 40°

∴ x = 60°

∴ x = 60°, y = 80°, z = 40°

Given: ∠BAD = 70°, ∠DER = 40°

Line AB || line DE and seg AD is their transversal.

∴ ∠EDA = ∠BAD … [Alternate Angles]

∴ ∠EDA = 70° … (I)

In ∆DRE,

∠EDR + ∠DER + ∠DRE = 180°

… [Since, sum of the measures of the angles of a triangle is 180°]

∴ 70° + 40° + ∠DRE = 180° [From (i) and D - R - A]

∴ ∠DRE = 180° - 70° - 40°

∴ ∠DRE = 70°

Also, ∠DRE + ∠ARE = 180° … [Angles in a linear pair]

∴ 70° + ∠ARE = 180°

∴ ∠ARE = 180° - 70°

∴ ∠ARE = 110°

∴ ∠DRE = 70°, ∠ARE = 110°

∠OAB = ∠OAC = ½ ∠BAC … (I) [Seg AO bisects ∠BAC]

∠OBA = ∠OBC = ½ ∠ABC … (II) [Seg RO bisects ∠ABC]

In ∆ABC,

∠BAC + ∠ABC + ∠ACB = 180°

… [Sum of the measures of the angles of a triangle is 180°]

∴ ∠BAC + ∠ABC + 70° = 180°

∴ ∠BAC + ∠ABC = 180° - 70°

∴ ∠BAC + ∠ABC = 110°

∴ ½ (∠BAC) + ½ (∠ABC) = ½ × 110°

… [Multiplying both sides by ½]

∴ ∠OAB + ∠OBA = 55° … (III) [From (I) and (II)]

In ∆OAB,

∠OAB + ∠OBA + ∠AOB = 180°

… [Sum of the measures of the angles of a triangle is 180°]

∴ 55° + ∠AOB = 180° … [From (III)]

∴ ∠AOB = 180° - 55°

∴ ∠AOB = 125°

Given: line AB || line CD and line PQ is the transversal.

Ray PT and ray QT are the bisectors of ∠BPQ and ∠PQD respectively.

To prove: m∠PTQ = 90°

Proof:

∠TPB = ∠TPQ = ½ ∠BPQ … (I) [Ray PT bisects ∠BPQ]

∠TQD = ∠TQP = ½ ∠PQD … (II) [Ray QT bisects ∠PQD]

Since, line AB || line CD and line PQ is their transversal.

∴ ∠BPQ + ∠PQD = 180° … [Interior angles]

∴ ½ (∠BPQ) + ½ (∠PQD) = ½ × 180° … [Multiplying both sides by ½]

∴ ∠TPQ + ∠TQP = 90°

In ∆PTQ,

∠TPQ + ∠TQP + ∠PTQ = 180°

… [Sum of the measures of the angles of a triangle is 180°]

∴ 90° + ∠PTQ = 180° … [From (III)]

∴ ∠PTQ = 180° - 90°

∴ m∠PTQ = 90°

∠c + 100° = 180° … [Angles in a linear pair]

∴ ∠c = 180° - 100°

∴ ∠c = 80° … (I)

∠b = 70° … (II) [Vertically opposite angles]

∠a + ∠b + ∠c = 180°

… [Since, sum of the measures of the angles of a triangle is 180°]

∴ ∠a + 70° + 80° = 180°

∴ ∠a = 180° - 70° - 80°

∴ ∠a = 30° … (III)

∴ ∠a = 30°, ∠b = 70°, ∠ c = 80°

(i)

∠DEG = ∠FEG = x° … (I) [Ray EG bisects ∠DEF]

∠GFD = ∠GFM = y° … (II) [Ray FG bisects ∠DFM]

Since, line DE || line GF and DF is their transversal.

∴ ∠EDF = ∠GFD … [Alternate angles]

∴ ∠EDF = y° … (III) [From (II)]

Since, line DE || line GF and EM is their transversal.

∴ ∠DEF = ∠GFM … [Corresponding angles]

∴ ∠DEG + ∠FEG = ∠GFM … [Angle addition property]

∴ x° + x° = y° … [From (I) and (II)]

∴ 2x° = y°

∴ x° = ½ y°

∴ ∠DEG = ½ ∠EDF … [From (I) and (III)]

(ii)

Since, line DE || line GF and GE is their transversal.

∴ ∠DEG = ∠FGE … (IV) [Alternate angles]

∴ ∠FEG = ∠FGE … (V) [From (I) and (IV)]

∴ In ∆FEG,

∠FEG = ∠FGE … [From (V)]

∴ EF = FG … [Converse of isosceles triangle theorem]

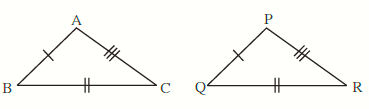
By SSS test

∆ ABC ≅ ∆ PQR

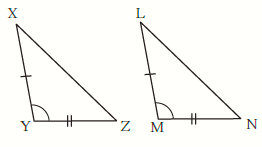
By SAS test

∆ XYZ ≅ ∆ LMN

By ASA test

∆ PRQ ≅ ∆ STU

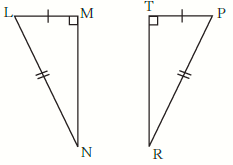
By hypotenuse side test

∆ LMN ≅ ∆ PTR

From the information shown in the figure,

in ∆ ABC and ∆ PQR

∠ABC ≅ ∠PQR

seg BC ≅ seg QR

∠ACB ≅ ∠PRQ

∴ ∆ABC ≅ ∆PQR .......test

∴ ∠BAC ≅ ....... Corresponding angles of congruent triangles.

seg AB ≅and ≅ seg PR …… corresponding sides of congruent triangles

In ∆BAC and ∆PQR,

seg BA ≅ seg PQ

seg BC ≅ seg PR

∠BAC ≅ ∠PQR = 90° … [Given]

∴ ∆BAC ≅ ∆PQR … [Hypotenuse side test]

∴ seg AC ≅ seg QR … [C.S.C.T]

∠ABC ≅ ∠QPR and ∠ACB ≅ ∠QRP … [C.A.C.T]

In ∆LMN and ∆PNM,

seg LM ≅ seg PN

seg LN ≅ seg PM … [Given]

seg MN ≅ seg NM … [Common side]

∴ ∆LMN ≅ ∆PNM … [SSS test]

Since, corresponding angles of congruent triangles are congruent

∴ ∠LMN ≅ ∠PNM,

∠MLN ≅ ∠NPM, and

∠LNM ≅ ∠PMN

In ∆ABD and ∆CBD,

seg AB ≅ seg CB

seg AD ≅ seg CD … [Given]

seg BD ≅ seg BD … [Common side]

∴ ∆ABD ≅ ∆CBD … [SSS test]

In ∆PQT and ∆RQS,

∠P ≅ ∠R … [Given]

seg PQ ≅ seg RQ … [Given]

∠Q ≅ ∠Q … [Common angle]

∴ ∆PQT ≅ ∆RQS … [By ASA test]

From the information shown in the figure,

In ∆ PTQ and ∆ STR

seg PT ≅ seg ST

∠PTQ ≅ ∠STR ... Vertically opposite angles

seg TQ ≅ seg TR

∠ACB = 50° … [Given]

In ∆ABC, seg AC ≅ seg AB … [Given]

∴ ∠ABC ≅ ∠ACB … [Isosceles triangle theorem]

∴ x = 50° … (I)

∠DBC = 60° … [Given]

In ABDC, seg BD ≅ seg DC … [Given]

∴ ∠DCB ≅ ∠DBC … [Isosceles triangle theorem]

∴ y = 60° … (II)

∠ABD = ∠ABC + ∠DBC … [Angle addition property]

= 50° + 60°

∴ ∠ABD = 110° … (III)

∠ACD = ∠ACB + ∠DCB … [Angle addition property]

= 50° + 60°

∴ ∠ACD = 110° … (IV)

Given: Length of hypotenuse = 15

In a right angled triangle, the length of the median on the hypotenuse is half the length of the hypotenuse

∴ Length of median on the hypotenuse = ½ × length of hypotenuse

= ½ × 15

= 7.5

∴ The length of the median on the hypotenuse is 7.5 units.

Given: PQ = 12, QR = 5

In APQR, ∠Q = 90° … (Given)

∴ PR₂ = QR₂ + PQ₂ … [Pythagoras theorem]

= 25 + 144

∴ PR₂ = 169

Taking square root of both sides

∴ PR = 13 units … (I)

Now, in right angled PQR, seg QS is the median on hypotenuse PR.

So, by using the property i.e. In a right angled triangle, the length of the median on the hypotenuse is half the length of the hypotenuse, we have

QS = ½ PR

= ½ × 13

∴ l(QS) = 6.5 units

In ∆PQR, G is the point of concurrence of the medians.

The centroid divides each median in the ratio 2 : 1.

PG : GT = 2 : 1

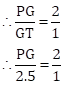
∴ PG = 2 × 2.5

∴ PG = 5 units

Now, PT = PG + GT [P - G - T]

= 5 + 2.5

∴ l(PG) = 5 units, l(PT) = 7.5 units

Given: AX = 2 cm

Since, point A lies on the bisector of ∠XYZ.

Also, every point on the bisector of an angle is equidistant from the sides of the angle.

∴ Point A is equidistant from the sides of ∠XYZ.

∴ AZ = AX

∴ AZ = 2 cm

Given: seg PT ⊥ ray ST, seg PR ⊥ ray SR and seg PR ≅ seg PT

Also, ∠RSP = 56° … (Given)

Any point equidistant from the sides of an angle is on the bisector of the angle.

∴ Point P lies on the bisector of ∠TSR

∴ Ray SP is the bisector of ∠RST.

∴ ∠RSP = ½ ∠RST

= ½ × 56°

∴ ∠RSP = 28°

In ∆PQR,

PQ = 10 cm, QR = 12 cm, PR = 8 cm … [Given]

Since, 12 > 10 > 8

∴ QR > PQ > PR

∴ ∠QPR > ∠PRQ > ∠PQR … [Angle opposite to greater side is greater]

∴ In ∆PQR, ∠QPR is the greatest angle and ∠PQR is the smallest angle.

In ∆FAN,

∠F + ∠A + ∠N = 180°

… [Sum of the measures of the angles of a triangle is 180°]

∴ 80° + 40° + ∠N = 180°

∴ ∠N = 180° - 80° - 40°

∴ ∠N = 60°

Since, 80° > 60° > 40°

∴ ∠F > ∠N > ∠A

∴ AN > FA > FN [Side opposite to greater angle is greater]

∴ In ∆FAN, AN is the greatest side and FN is the smallest side.

∆ABC is an equilateral triangle.

To prove: ∆ABC is equiangular

i.e. seg AB ≅ seg BC ≅ seg AC … (I) [Sides of an equilateral triangle]

In ∆ABC,

seg AB ≅ seg BC … [From (I)]

∴ ∠C ≅ ∠A … (II) [Isosceles triangle theorem]

In ∆ABC,

seg BC ≅ seg AC … [From (I)]

∴ ∠A ≅ ∠B … (III) [Isosceles triangle theorem]

∴ ∠A ≅ ∠B ≅ ∠C … [From (II) and (III)]

∴ ∆ABC is equiangular.

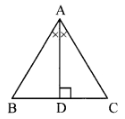
Given: Seg AD is the bisector of ∠BAC and seg AD ⊥ seg BC

To prove: ∆ABC is an isosceles triangle.

Proof:

In ∆ABD and ∆ACD,

∠BAD ≅ ∠CAD … [seg AD is the bisector of ∠BAC]

seg AD ≅ seg AD … [Common side]

∠ADB ≅ ∠ADC … [Each angle is of measure 90°]

∴ ∆ABD ≅ ∆ACD … [ASA test]

∴ seg AB ≅ seg AC … [C.S.C.T.]

∴ ∆ABC is an isosceles triangle.

In ∆PQR,

seg PR ≅ seg PQ … [Given]

∴ ∠PQR ≅ ∠PRQ … (I) [Isosceles triangle theorem]

Since, ∠PRQ is the exterior angle of ∆PRS.

∴ ∠PRQ > ∠PSR … (II) [Property of exterior angle]

∴ ∠PQR > ∠PSR … [From (i) and (ii)]

i.e. ∠Q > ∠S … (III)

In ∆PQS,

∠Q > ∠S … [From (III)]

∴ PS > PQ … [Side opposite to greater angle is greater]

∴ seg PS > seg PQ

In ∆ADB and ∆BEA,

seg BD ≅ seg AE … [Given]

∠ADB ≅ ∠BEA = 90° … [Given]

seg AB ≅ seg BA … [Common side]

∴ ∆ADB ≅ ∆BEA … [Hypotenuse-side test]

∴ seg AD ≅ seg BE … [C.S.C.T.]

Given: ∆XYZ ~ ∆LMN

∴ ∠X ≅ ∠L, ∠Y ≅ ∠M, ∠Z ≅ ∠N … [Corresponding angles of similar triangles]

Also, the corresponding sides of similar triangles are in the same ratio.

Given: ΔXYZ ~ ΔPQR

So, the corresponding sides of these triangles will be in the same ratio

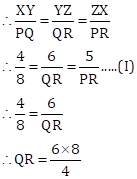
∴ QR = 12 cm

From (I), we have

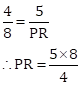
∴ PR = 10 cm

Thus, the lengths of the sides QR and PR are 12 cm and 10 cm respectively.

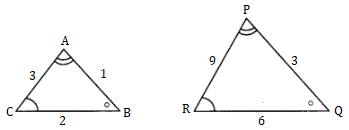
ΔABC ~ ΔPQR

In ∆PQS,

PQ + QS > PS … (I)

… [Sum of any two sides of a triangle is greater than the third side]

Similarly, in ∆PSR,

PR + SR > PS … (II)

… [Sum of any two sides of a triangle is greater than the third side]

∴ PQ + QS + PR + SR > PS + PS

∴ PQ + QS + SR + PR > 2PS

∴ PQ + QR + PR > 2PS … [Q-S-R]

Given: Bisector of ∠BAC intersects side BC at point D.

To prove: AB > BD

Proof:

∠BAD ≅ ∠DAC … (I) [Seg AD bisects ∠BAC]

∠ADB is the exterior angle of ∆ADC.

∴ ∠ADB >∠DAC … (II) [Property of exterior angle]

∴ ∠ADB >∠BAD … (III) [From (I) and (II)]

In ∆ABD,

∠ADB >∠BAD … [From (III)]

∴ AB >BD … [Side opposite to greater angle is greater]

Given: Seg PT is the bisector of ∠QPR.

To prove: PS = PR

Construction: Draw seg SR || seg PT.

Proof:

Given: seg PT is the bisector of ∠QPR

∴ ∠QPT = ∠RPT … (I)

Now, seg PT || seg SR and seg QS is their transversal.

∴ ∠QPT = ∠PSR … (II) [Corresponding angles]

Again, seg PT || seg SR and seg PR is their transversal.

∴ ∠RPT = ∠PRS … (III) [Alternate angles]

∴ ∠PRS = ∠PSR … (IV) [From (I), (II) and (III)]

In ∆PSR,

∠PRS = ∠PSR … From (IV)

∴ PS = PR … [Converse of isosceles triangle theorem]

Given: seg AD ⊥ seg BC and seg AE is the bisector of ∠CAB.

To prove: ∠DAE = ½ (∠C - ∠B)

Proof:

∴ ∠CAE = ½ ∠A … (I) [Since, seg AE is the bisector of ∠CAB]

In ∆DAE,

∠DAE + ∠ADE + ∠AED = 180°

… [Sum of the measures of the angles of a triangle is 180°]

∴ ∠DAE + 90° + ∠AED = 180° … [∵ AD ⊥ BC]

∴ ∠DAE = 180° - 90° - ∠AED

∴ ∠DAE = 90° - ∠AED … (II)

In ∆ACE,

∠ACE + ∠CAE + ∠AEC = 180°

… [Sum of the measures of the angles of a triangle is 180°]

∠C + ½ ∠A + ∠AED = 180° [From (I) and C-D-E]

∴ ∠AED = 180° - ∠C - ½ ∠A … (III)

Substituting this value of ∠AED in (II)

∴ ∠DAE = 90° - 180° + ∠C + ½ ∠A

∴ ∠DAE = ∠C + ½ ∠A - 90° … (IV)

Now, in ∆ABC,

∠A + ∠B + ∠C = 180°

Dividing both sides by 2

(D)

We know that, sum of any two sides of a triangle is greater than the third side.

But for 1.5 cm and 3.4 cm,

1.5 + 3.4 = 4.9 cm < 5 cm

So, the third side can't be 3.4 cm.

(B)

In ΔPQR, ∠R > ∠Q

Since, the side opposite to greater angle is greater.

∴ PQ >PR

(B)

Given: ∠T = 65°, ∠P = 95°

∴ 65° < 95°

∴ ∠T < ∠P

Since, the side opposite to smaller angle is smaller.

∴ PQ

Given: AB = AC, seg BD and seg CE are the medians of ∆ABC

To prove: BD = CE

Proof:

AE = ½ AB … (I) [E is the midpoint of side AB]

AD = ½ AC … (II) [D is the midpoint of side AC]

Also, AB = AC … (III) [Given]

∴ AE = AD … (IV) [From (I), (II) and (III)]

In ∆ADB and ∆AEC,

seg AB ≅ seg AC … (Given)

∠BAD ≅ ∠CAE … (Common angle)

seg AD ≅ seg AE … From (IV)

∴ ∆ADB ≅ ∆AEC

∴ seg BD ≅ seg CE … [CPCT]

∴ BD = CE

Given: In APQR, PQ > PR and bisectors of ∠Q and ∠R intersect at S.

To prove: SQ > SR

Proof:

∠SQR = ½ ∠PQR … (I) [Ray QS bisects ∠PQR]

∠SRQ = ½ ∠PRQ … (II) [Ray RS bisects ∠PRQ]

In ∆PQR,

PQ > PR … Given

∴ ∠R > ∠Q … Angle opposite to greater side is greater

∴ ½ (∠R) > ½ (∠Q) … Multiplying both sides by ½

∴ ∠SRQ >∠SQR … (III) [From (I) and (II)]

∴ In ∆SQR, ∠SRQ >∠SQR … From (III)

∴ SQ >SR … [Side opposite to greater angle is greater]

Given: Points D and E are on side BC of ∆ABC, such that BD = CE and AD = AE.

To prove: ∆ABD ≅ ∆ACE

Proof:

In ∆ADE,

seg AD = seg AE … Given

∴ ∠AED = ∠ADE … (I) [Isosceles triangle theorem]

Now, ∠ADE + ∠ADB = 180° … (II) [Angles in a linear pair]

Also, ∠AED + ∠AEC = 180° … (III) [Angles in a linear pair]

∴ ∠ADE + ∠ADB = ∠AED + ∠AEC … [From (II) and (III)]

∴ ∠ADE + ∠ADB = ∠ADE + ∠AEC … [From (I)]

∴ ∠ADB = ∠AEC … (IV) [Eliminating ∠ADE from both sides]

In ∆ABD and ∆ACE,

seg BD ≅ seg CE … (Given)

∠ADB = ∠AEC … From (IV)

seg AD ≅ seg AE … (Given)

∴ ∆ABD ≅ ∆ACE … (SAS test)