Class 9 MAHARASHTRA STATE TEXTBOOK BUREAU Solutions Maths Chapter 5 - Quadrilaterals

∠XYZ = 135°

and WXYZ is a parallelogram.

∠XWZ = ∠XYZ

∴ ∠XWZ = 135° …..(i)

∠YZW + ∠XYZ = 180° [Adjacent angles of a parallelogram are supplementary]

∴ ∠YZW + 135°= 180° [From (i)]

∴ ∠YZW = 180°- 135°

∴ ∠YZW = 45°

l(OY) = 5 cm [Given]

l(OY) =× l(WY) [Diagonals of a parallelogram bisect each other]

∴ l(WY) = 2 × l(OY)

= 2 × 5

∴ l(WY) = 10 cm

∴∠XWZ = 135°, ∠YZW = 45°, l(WY) = 10 cm

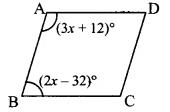
ABCD is a parallelogram. [Given]

∴ ∠A + ∠B = 180° [Adjacent angles of a parallelogram are supplementary],

∴ (3x + 12)° + (2x-32)° = 180°

∴ 3x + 12° + 2x - 32° = 180°

∴ 5x - 20° = 180°

∴ 5x= 180° + 20°

∴ 5x = 200°

∴ x = 40°

∠A = (3x + 12)°

= [3(40) + 12]°

=(120 +12)°= 132°

∠B = (2x - 32)°

= [2(40) - 32]°

= (80 - 32)° = 48°

∴ ∠C = ∠A = 132°

∠D = ∠B = 48° [Opposite angles of a parallelogram]

∴ The value of x is 40, and the measures of ∠C and ∠D are 132° and 48° respectively.

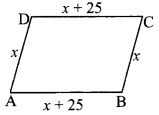
Let, ABCD be the parallelogram and the length of AD be x cm.

One side is greater than the other by 25 cm.

∴ AB = x + 25 cm

AD = BC = x cm

AB = DC = (x + 25) cm [Opposite angles of a parallelogram]

Perimeter of ABCD = 150 cm [Given]

∴ AB + BC + DC + AD = 150

∴ (x + 25) +x + (x + 25) + x - 150

∴ 4x + 50 = 150

∴ 4x = 150 - 50

∴ 4x = 100

∴ x = 25

AD = BC = x = 25 cm

AB = DC = x + 25 = 25 + 25 = 50 cm

∴ The lengths of the sides of the parallelogram are 25 cm, 50 cm, 25 cm and 50 cm.

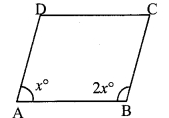
Let ABCD be the parallelogram.

The ratio of measures of two adjacent angles of a parallelogram is 1 : 2.

Let the common multiple be x.

∴ ∠A = x and ∠B = 2x

∠A + ∠B = 180° [Adjacent angles of a parallelogram are supplementary]

∴ x + 2x = 180°

∴ 3x = 180°

∴ x = 60°

 ∠A = x° = 60°

∠B = 2x° = 2 x 60° = 120°

∠A = ∠C = 60°

∠B = ∠D= 120° [Opposite angles of a parallelogram]

∴ The measures of the angles of the parallelogram are 60°, 120°, 60° and 120°.

Given: AO = 5, BO = 12 and AB = 13.

To prove: □ABCD is a rhombus.

Solution:

Proof:

AO = 5, BO = 12, AB = 13 [Given]

AO² + BO² = 5² + 12²

= 25 + 144

∴ AO² + BO² = 169 …..(i)

AB² = 13² = 169 ….(ii)

∴ AB2 = AO² + BO² [From (i) and (ii)]

∴ ∆AOB is a right-angled triangle. [Converse of Pythagoras theorem]

∴ ∠AOB = 90°

∴ seg AC ⊥ seg BD …..(iii) [A-O-C]

∴ In parallelogram ABCD,

∴ seg AC ⊥ seg BD [From (iii)]

∴ ABCD is a rhombus. [A parallelogram is a rhombus perpendicular to each other]

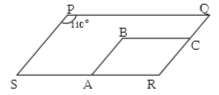
PQRS is a parallelogram. [Given]

∴ ∠R = ∠P [Opposite angles of a parallelogram]

∴ ∠R = 110° …..(iii)

ABCR is a parallelogram. [Given]

∴ ∠A + ∠R= 180° [Adjacent angles of a parallelogram are supplementary]

∴ ∠A+ 110°= 180° [From (i)]

 ∴ ∠A= 180°- 110°

∴ ∠A = 70°

∴ ∠C = ∠A = 70°

∴ ∠B = ∠R= 110° [Opposite angles of a parallelogram]

∴ ∠A = 70°, ∠B = 110°,

∴ ∠C = 70°, ∠R = 110°

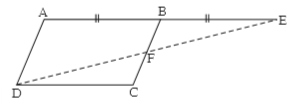
Given: ABCD is a parallelogram.

BE = AB

To prove: Line ED bisects seg BC at point F i.e. FC = FB

Solution:

Proof:

ABCD is a parallelogram. [Given]

∴ seg AB ≅ seg DC …….(i) [Opposite angles of a parallelogram]

seg AB ≅ seg BE ……..(ii) [Given]

seg DC ≅ seg BE ……..(iii) [From (i) and (ii)]

side DC || side AB [Opposite sides of a parallelogram]

i.e. side DC || seg AE and seg DE is their transversal. [A-B-E]

∴ ∠CDE ≅ ∠AED

∴ ∠CDF ≅ ∠BEF …..(iv) [D-F-E, A-B-E]

In ∆DFC and ∆EFB,

seg DC = seg EB [From (iii)]

∠CDF ≅ ∠BEF [From (iv)]

∠DFC ≅ ∠EFB [Vertically opposite angles]

∴ ∆DFC ≅ ∆EFB [SAA test]

∴ FC ≅ FB [c.s.c.t]

∴ Line ED bisects seg BC at point F.

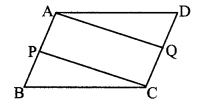
Given: ABCD is a parallelogram. P and Q are the midpoints of sides AB and DC respectively.

To prove: APCQ is a parallelogram.

Solution:

Proof:

AP =AB …..(i) [P is the midpoint of side AB]

QC =DC ….(ii) [Q is the midpoint of side CD]

ABCD is a parallelogram. [Given]

∴ AB = DC [Opposite sides of a parallelogram]

∴AB =DC [Multiplying both sides by 12]

∴ AP = QC ….(iii) [From (i) and (ii)]

Also, AB || DC [Opposite angles of a parallelogram]

i.e. AP || QC ….(iv) [A - P - B, D - Q - C]

From (iii) and (iv),

APCQ is a parallelogram. [A quadrilateral is a parallelogram if its opposite sides is parallel and congruent]

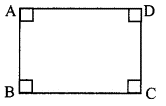
Given:

ABCD is a rectangle.

To prove: Rectangle ABCD is a parallelogram.

Solution:

Proof:

ABCD is a rectangle.

∴ ∠A ≅ ∠C = 90° [Given]

∠B ≅ ∠D = 90° [Angles of a rectangle]

∴ Rectangle ABCD is a parallelogram. [A quadrilateral is a parallelogram, if pairs of its opposite angles are congruent]

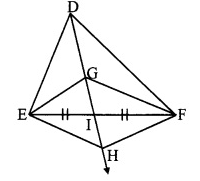
Given: Point G (centroid) is the point of concurrence of the medians of ∆DEF. DG = GH

To prove: GEHF is a parallelogram.

Solution:

Proof:

Let ray DH intersect seg EF at point I such that E-I-F.

∴ seg DI is the median of ∆DEF.

∴ El = FI ……(i)

Point G is the centroid of ∆DEF.

[Centroid divides each median in the ratio 2:1]

∴ DG = 2(GI)

∴ GH = 2(GI) [DG = GH]

∴ GI + HI = 2(GI) [G-I-H]

∴ HI = 2(GI) - GI

∴ HI = GI ….(ii)

From (i) and (ii),

GEHF is a parallelogram [A quadrilateral is a parallelogram, if its diagonals bisect each other]

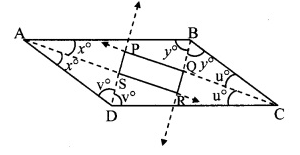
Given: ABCD is a parallelogram.

Rays AS, BQ, CQ and DS bisect ∠A, ∠B, ∠C and ∠D respectively.

To prove: PQRS is a rectangle.

Solution:

Proof:

∠BAS = ∠DAS = x° …(i) [ray AS bisects ∠A]

∠ABQ = ∠CBQ =y° ….(ii) [ray BQ bisects ∠B]

∠BCQ = ∠DCQ = u° …..(iii) [ray CQ bisects ∠C]

∠ADS = ∠CDS = v° ….(iv) [ray DS bisects ∠D]

□ABCD is a parallelogram. [Given]

∴ ∠A + ∠B = 180° [Adjacent angles of a parallelogram are supplementary]

∴ ∠BAS + ∠DAS + ∠ABQ + ∠CBQ = 180° [Angle addition property]

∴ x°+x°+ v° + v° = 180 [From (i) and (ii)]

∴ 2x° + 2v° =180

∴ x + y = 90° ……(v) [Dividing both sides by 2]

Also, ∠A + ∠D= 180° [Adjacent angles of a parallelogram are supplementary]

∴ ∠BAS + ∠DAS + ADS + ∠CDS = 180° [Angle addition property]

∴ x° + x° + v° + v° = 180°

∴ 2x° + 2v° = 180°

∴ x° + v° = 90° …..(vi) [Dividing both sides by 2]

In ∆ARB,

∠RAB + ∠RBA + ∠ARB = 180° [Sum of the measures of the angles of a triangle is 180°]

∴ x° + y° + ∠SRQ = 180° [A - S - R, B - Q - R]

∴ 90° + ∠SRQ = 180° [From (v)

∴ ∠SRQ = 180°- 90° = 90° …..(vi)

Similarly, we can prove

∠SPQ = 90° …(viii)

In ∆ASD,

∠ASD + ∠SAD + ∠SDA = 180° [Sum of the measures of angles a triangle is 180°]

∴ ∠ASD + x° + v° = 180° [From (vi)]

∴ ∠ASD + 90° = 180°

∴∠ASD = 180°- 90° = 90°

∴ ∠PSR = ∠ASD [Vertically opposite angles]

∴ ∠PSR = 90° …..(ix)

Similarly we can prove

∠PQR = 90° ..(x)

∴ In PQRS,

∠SRQ = ∠SPQ = ∠PSR = ∠PQR = 90° [From (vii), (viii), (ix), (x)]

∴ PQRS is a rectangle. [Each angle is of measure 90°]

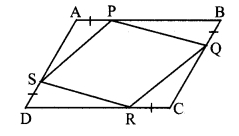
Given: ABCD is a parallelogram.

AP = BQ = CR = DS

To prove: PQRS is a parallelogram.

Solution:

Proof:

ABCD is a parallelogram. [Given]

∴ ∠B = ∠D ….(i) [Opposite angles of a parallelogram]

Also, AB = CD [Opposite sides of a parallelogram]

∴ AP + BP = DR + CR [A-P-B, D-R-C]

∴ AP + BP = DR + AP [AP = CR]

∴ BP = DR ….(ii)

In APBQ and ARDS,

seg BP ≅ seg DR [From (ii)]

∠PBQ ≅ ∠RDS [From (i)]

seg BQ ≅ seg DS [Given]

∴ ∆PBQ ≅ ∆RDS [SAS test]

∴ seg PQ ≅ seg RS …..(iii) [c.s.c.t]

Similarly, we can prove that

∆PAS ≅ ∆RCQ

∴ seg PS ≅ seg RQ ….(iv) [c.s.c.t]

From (iii) and (iv),

PQRS is a parallelogram. [A quadrilateral is a parallelogram, if pairs of its opposite angles are congruent]

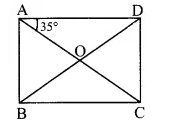
AC = 8 cm …(i) [Given]

ABCD is a rectangle [Given]

∴ BD = AC [Diagonals of a rectangle are congruent]

∴ BD = 8 cm [From (i)]

BO = 1/2 BD [Diagonals of a rectangle bisect each other]

∴ BO = 1/2 x 8

∴ BO = 4 cm

Side AD || side BC and seg AC is their transversal. [Opposite sides of a rectangle are parallel]

∴ ∠ACB = ∠CAD [Alternate angles]

∠ACB = 35° [ ∵∠CAD = 35°]

∴ BO = 4 cm, ∠ACB = 35°

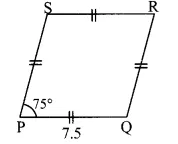
PQ = 7.5 cm [Given]

PQRS is a rhombus. [Given]

∴ QR = PQ [Sides of a rhombus are congruent]

∴ QR = 7.5 cm

∠QPS = 75° [Given]

∠QPS + ∠PQR = 180° [Adjacent angles of a rhombus are supplementary]∴ 75° + ∠PQR = 180°

∴ ∠PQR = 180° - 75°

∴ ∠PQR =105°

∠SRQ = ∠QPS [Opposite angles of a rhombus]

∴ ∠SRQ = 75°

∴ QR = 7.5 cm, ∠PQR = 105°,

∠SRQ = 75°

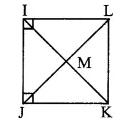
IJKL is a square. [Given]

∴ seg IK ⊥ seg JL [Diagonals of a square are perpendicular to each other]

∠ IMJ=90°

∠ JIL = 90° ……. (i) [Angle of a square]

∠JIK = 1/2∠JIL [Diagonals of a square bisect the opposite angles]

∠JIK = 1/2 (90°) [From (i)

∴ ∠JIK = 45°

∠IJK = 90° (ii) [Angle of a square]

∠LJK = 1/2∠IJK [Diagonals of a square bisect the opposite angles]

∠LJK = 1/2 (90°) [From (ii)]

∴ ∠LJK = 45°

∴ ∠LJK = 90°, ∠JIK = 45°, ∠LJK=45°

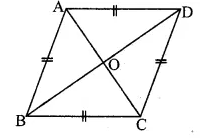
Let ABCD be the rhombus. AC = 20 cm, BD = 21 cm

In ∆AOB, ∠AOB = 90° [Diagonals of a rhombus are perpendicular to each other]

∴ AB² = AO² + BO² [Pythagoras theorem]

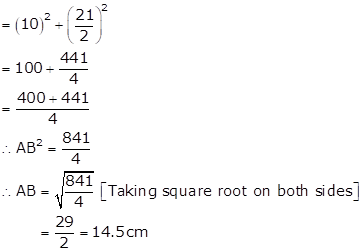
Perimeter of ABCD

= 4 x AB = 4 x 14.5 = 58 cm

∴ The side and perimeter of the rhombus are 14.5 cm and 58 cm respectively.

i. False.

All the sides of a rhombus are congruent, while the opposite sides of a parallelogram are congruent.

ii. False.

All the angles of a rectangle are congruent, while the opposite angles of a rhombus are congruent.

iii. True.

The opposite sides of a parallelogram are parallel and congruent. Also, its opposite angles are congruent.

The opposite sides of a rectangle are parallel and congruent. Also, all its angles are congruent.

iv. True.

The opposite sides of a rectangle are parallel and congruent. Also, all its angles are congruent.

All the sides of a square are parallel and congruent. Also, all its angles are congruent.

v. True.

All the sides of a rhombus are congruent. Also, its diagonals are perpendicular bisectors of each other.

All the sides of a square are congruent. Also, its diagonals are perpendicular bisectors of each other.

vi. False.

All the angles of a rectangle are congruent, while the opposite angles of a parallelogram are congruent.

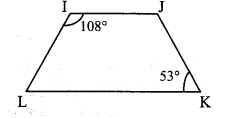
∠I = 108° [Given]

Side IJ || side KL and side IL is their transversal. [Given]

∴ ∠I + ∠L = 180° [Interior angles]

∴ 108° + ∠L = 180°

∴ ∠L = 180° - 108° = 72°

∠K = 53° [Given]

Side IJ || side KL and side JK is their transversal. [Given]

∴ ∠J + ∠K = 180° [Interior angles]

∴ ∠J + 53° = 180°

∴ ∠J= 180°- 53° = 127°

∴ ∠L = 72°, ∠J = 127°

∠A = 72° [Given]

In □ABCD, side BC || side AD and side AB is their transversal. [Given]

∴ ∠A + ∠B = 180° [Interior angles]

∴ 72° +∠B = 180°

∴ ∠B = 180° - 72° = 108°

In ∆BPA and ∆CQD,

∠BPA ≅ ∠CQD [Each angle is of measure 90°]

Hypotenuse AB ≅ Hypotenuse DC [Given]

seg BP ≅ seg CQ [Perpendicular distance between two parallel lines]

∴ ∆BPA ≅ ∆CQD [Hypotenuse side test]

∴ ∠BAP ≅ ∠CDQ [c. a. c. t.]

∴ ∠A = ∠D

∴ ∠D = 72°

∴ ∠B = 108°, ∠D = 72°

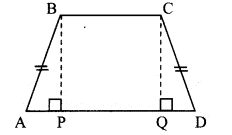
Given: side BC < side AD, side BC || side AD, side BA = side CD

To prove: ∠ABC ≅ ∠DCB

Construction: Draw seg BP ⊥ side AD, (A - P - D)

seg CQ ⊥ side AD, (A - Q - D)

Solution:

Proof:

In ∆BPA and ∆CQD,

∠BPA ≅ ∠CQD [Each angle is of measure 90°]

Hypotenuse BA ≅ Hypotenuse CD [Given]

seg BP ≅ seg CQ [Perpendicular distance between two parallel lines]

∴ ∆BPA ≅ ∆CQD [Hypotenuse side test]

∴ ∠BAP ≅ ∠CDQ [c. a. c. t.]

∴ ∠A = ∠D ….(i)

Now, side BC || side AD and side AB is their transversal. [Given]

∴ ∠A + ∠B = 180°…..(ii) [Interior angles]

Also, side BC || side AD and side CD is their transversal. [Given]

∴ ∠C + ∠D = 180° …..(iii) [Interior angles]

∴ ∠A + ∠B = ∠C + ∠D [From (ii) and (iii)]

∴ ∠A + ∠B = ∠C + ∠A [From (i)]

∴ ∠B = ∠C

∴ ∠ABC ≅ ∠DCB

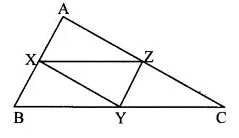
AC = 9 cm [Given]

Points X and Y are the midpoints of sides AB and BC respectively. [Given]

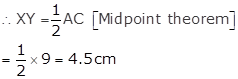
AB = 5 cm [Given]

Points Y and Z are the midpoints of sides BC and AC respectively. [Given]

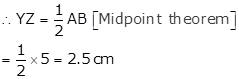
BC = 11 cm [Given]

Points X and Z are the midpoints of sides AB and AC respectively. [Given]

∴ XZ =BC [Midpoint theorem]

=× 11 = 5.5 cm

l(XY) = 4.5 cm, l(YZ) = 2.5 cm, l(XZ) = 5.5 cm

Given: PQRS and MNRL are rectangles. M is the midpoint of side PR.

Solution:

To prove:

i. SL = LR

ii. LN = (SQ)

Proof:

PQRS and MNRL are rectangles. [Given]

∴ ∠S = ∠L = 90° [Angles of rectangles]

∠S and ∠L form a pair of corresponding angles on sides SP and LM when SR is their transversal.

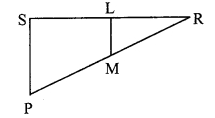
∴eg, ML || seg PS …(i) [Corresponding angles test]

In ∆PRS,

Point M is the midpoint of PR and seg ML || seg PS. [Given] [From (i)]

∴ Point L is the midpoint of seg SR. ……(ii) [Converse of midpoint theorem]

∴ SL = LR

Similarly, for ∆PRQ, we can prove that,

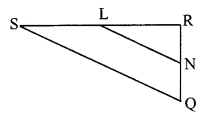
Point N is the midpoint of seg QR. ….(iii)

In ∆RSQ,

Points L and N are the midpoints of seg SR and seg QR respectively. [From (ii) and (iii)]

∴ LN =SQ [Midpoint theorem]

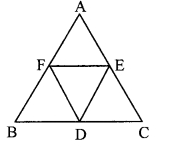
Given: ∆ABC is an equilateral triangle.

Points F, D and E are midpoints of side AB, side BC, side AC respectively.

To prove: ∆FED is an equilateral triangle.

Solution:

Proof:

∆ABC is an equilateral triangle. [Given]

∴ AB = BC = AC ….(i) [Sides of an equilateral triangle]

Points F, D and E are midpoints of side AB and BC respectively.

∴ FD =AC …..(ii) [Midpoint theorem]

Points D and E are the midpoints of sides BC and AC respectively.

Points F and E are the midpoints of sides AB and AC respectively.

∴ FE = BC

∴ FD = DE = FE [From (i), (ii), (iii) and (iv) ]

∴ ∆FED is an equilateral triangle.

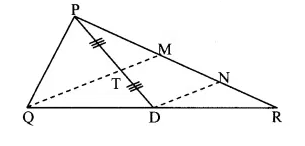
Given: seg PD is a median of ∆PQR. Point T is the midpoint of seg PD.

To Prove:

Construction: Draw seg DN || seg QM such that P-M-N and M-N-R.

Proof:

In ∆PDN,

Point T is the midpoint of seg PD and seg TM || seg DN [Given]

∴ Point M is the midpoint of seg PN. [Construction and Q-T-M]

∴ PM = MN [Converse of midpoint theorem]

In ∆QMR,

Point D is the midpoint of seg QR and seg DN || seg QM [Construction]

∴ Point N is the midpoint of seg MR. [Converse of midpoint theorem]

∴ RN = MN …..(ii)

∴ PM = MN = RN …..(iii) [From (i) and (ii)]

Now, PR = PM + MN + RN [ P-M-R-Q-T-M]

∴ PR = PM + PM + PM [From (iii) ]

∴ PR = 3PM

(d) rhombus

In ∆ABC,

AC² = AB² + BC²

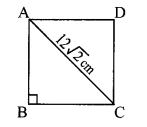
∴ AB = 12 cm

∴ Perimeter of ABCD = 4 x 12 = 48 cm

(c) 48 cm

2x = 3x - 40 … [Pythagoras theorem]

∴ x = 40°

(d) 40°

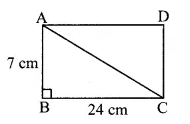
Let ABCD be the rectangle.

AB = 7 cm, BC = 24 cm

In ∆ABC, ∠B = 90° [Angle of a rectangle]

AC² = AB² + BC² [Pythagoras theorem]

= 7² + 24²

= 49 + 576

= 625

AC = [Taking square root of both sides]

= 25 cm

∴ The length of the diagonal of the rectangle is 25 cm.

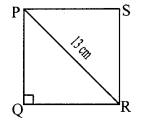
Let PQRS be the square of side x cm.

∴ PQ = QR = x cm …..(i) [Sides of a square]

∴ In ∆PQR, ∠Q = 90° [Angle of a square]

∴ PR² = PQ² + QR² [Pythagoras theorem]

∴ 13 = x + x [From (i)]

∴ 169 = 2x²

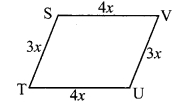
Let STUV be the parallelogram.

Ratio of two adjacent sides of a parallelogram is 3 : 4.

Let the common multiple be x.

ST = 3x cm and TU = 4x cm

∴ ST = UV = 3x cm

TU = SV = 4x cm …..(i) [Opposite sides of a parallelogram]

Perimeter of STUV = 112 [Given]

∴ ST + TU + UV + SV = 112

∴ 3x + 4x + 3x + 4x = 112 [From (i)]

∴ 14x = 112

∴ x = 8

∴ ST = UV = 3x = 3 x 8 = 24 cm

∴ TU = SV = 4x = 4 x 8 = 32 cm [From (i)]

∴ The lengths of the sides of the parallelogram are 24 cm, 32 cm, 24 cm and 32 cm.

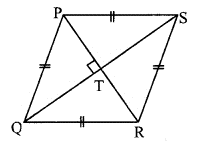
PQRS is a rhombus. [Given]

PR = 20 cm and QS = 48 cm [Given]

∴ PT =PR [Diagonals of a rhombus bisect each other]

=× 20 = 10 cm

Also, QT =QS [Diagonals of a rhombus bisect each other]

=× 48 = 24 cm

ii. In ∆PQT, ∠PTQ = 90° [Diagonals of a rhombus are perpendicular to each other]

∴ PQ^² = PT^² + QT^²[Pythagoras- theorem]

= 10^²+ 24^²

= 100 + 576

∴ PQ²= 676

∴ PQ = [Taking square root of both sides]

= 26 cm

∴ The length of side PQ is 26 cm.

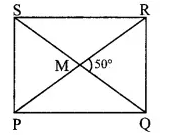
PQRS is a rectangle.

∴ PM =PR …(i)

MS =QS …(ii) [Diagonals of a rectangle bisect each other]

Also, PR = QS …..(iii) [Diagonals of a rectangle are congruent]

∴ PM = MS ….(iv) [From (i), (ii) and (iii)]

In ∆PMS,

PM = MS [From (iv)]

∴ ∠MSP = ∠MPS = x° …..(v) [Isosceles triangle theorem]

∠PMS = ∠QMR = 50° ……(vi) [Vertically opposite angles]

In ∆MPS,

∠PMS + ∠MPS + ∠MSP = 180° [Sum of the measures of the angles of a triangle is 180°]

∴ 50° + x + x = 180° [From (v) and (vi)]

∴ 50° + 2x= 180

∴ 2x= 180-50

∴ 2x= 130

∴ x == 65°

∴ ∠MPS = 65° [From (v)]

Solution:

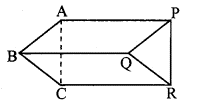
Given: seg AB || seg PQ , seg AB ≅ seg PQ,

seg AC || seg PR, seg AC ≅ seg PR

To prove: seg BC || seg QR, seg BC ≅ seg QR

Proof:

Consider □ABQP,

seg AB || seg PQ [Given]

seg AB ≅ seg PQ [Given]

∴ ABQP is a parallelogram. [A quadrilateral is a parallelogram if a pair of its opposite sides is parallel and congruent]

∴ seg AP || seg BQ …..(i)

∴ seg AP ≅ seg BQ …..(ii) [Opposite sides of a parallelogram]

Consider □ACRP,

seg AC || seg PR [Given]

seg AC ≅ seg PR [Given]

∴ ACRP is a parallelogram. [A quadrilateral is a parallelogram if a pair of its opposite sides is parallel and congruent]

∴ seg AP || seg CR …(iii)

∴ seg AP ≅ seg CR …….(iv) [Opposite sides of a parallelogram]

Consider □BCRQ,

seg BQ || seg CR

seg BQ ≅ seg CR

∴ BCRQ is a parallelogram. [A quadrilateral is a parallelogram if a pair of its opposite sides is parallel and congruent]

∴ seg BC || seg QR

∴ seg BC ≅ seg QR [Opposite sides of a parallelogram]

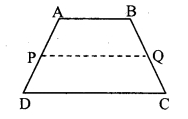
Given : ABCD is a trapezium.

To prove:

Construction: Join points A and Q. Extend seg AQ and let it meet produced DC at R.

Proof:

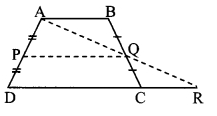
seg AB || seg DC [Given]

and seg BC is their transversal.

∴ ∠ABC ≅ ∠RCB [Alternate angles]

∴ ∠ABQ ≅ ∠RCQ ….(i) [B-Q-C]

In ∆ABQ and ∆RCQ,

∠ABQ ≅ ∠RCQ [From (i)]

seg BQ ≅ seg CQ [Q is the midpoint of seg BC]

∠BQA ≅ ∠CQR [Vertically opposite angles]

∴ ∆ABQ ≅ ∆RCQ [ASA test]

seg AB ≅ seg CR …(ii) [c. s. c. t.]

seg AQ ≅ seg RQ [c. s. c. t.]

∴ Q is the midpoint of seg AR. ….(iii)

In ∆ADR,

Points P and Q are the midpoints of seg AD and seg AR respectively. [Given and from (iii)]

∴ seg PQ || seg DR [Midpoint theorem]

i.e. seg PQ || seg DC ……..(iv) [D-C-R]

But, seg AB || seg DC …….(v) [Given]

∴ seg PQ || seg AB [From (iv) and (v)]

In ∆ADR,

PQ =DR [Midpoint Theorem]

=(DC +CR) [D-C-R]

=(DC + AB) [From (iii)]

PQ =(AB + DC)

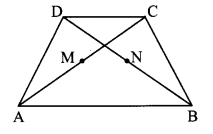
Solution:

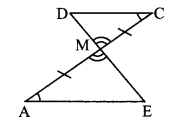
Given: ABCD is a trapezium. AB || DC.

Points M and N are midpoints of diagonals AC and DB respectively.

To prove: MN || AB

Construction: Join D and M. Extend seg DM to meet seg AB at point E such that A-E-B.

Proof:

seg AB || seg DC and seg AC is their transversal. [Given]

∴ ∠CAB ≅ ∠ACD [Alternate angles]

∴ ∠MAE ≅ ∠MCD ….(i) [C-M-A, A-E-B]

In ∆AME and ∆CMD,

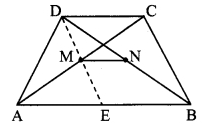
∠AME ≅ ∠CMD [Vertically opposite angles]

seg AM ≅ seg CM [M is the midpoint of seg AC]

∠MAE ≅ ∠MCD [From (i)]

∴ ∆AME ≅ ∆CMD [ASA test]

∴ seg ME ≅ seg MD [c.s.c.t]

∴ Point M is the midpoint of seg DE. …(ii)

In ∆DEB,

Points M and N are the midpoints of seg DE and seg DB respectively. [Given and from (ii)]

∴ seg MN || seg EB [Midpoint theorem]

∴ seg MN || seg AB [A-E-B]