Class 9 MAHARASHTRA STATE TEXTBOOK BUREAU Solutions Maths Chapter 2 - Parallel Lines

(i)

∠DHP = 85° … (I)

∠DHP + ∠RHD = 180° … [Angles in a linear pair]

∴ 85° + ∠RHD = 180°

∴ ∠RHD = 180° - 85°

∴ ∠RHD = 95° … (II)

(ii)

∠PHG = ∠RHD … [Vertically opposite angles]

∴ ∠PHG = 95° … [From (II)]

(iii) Line RP || line MS and line DK is their transversal.

∴ ∠HGS = ∠DHP … [Corresponding angles]

∴ ∠HGS = 85° … [From (I)]

(iv)

∠HGS = 85° … (III)

∴ ∠MGK = ∠HGS … [Vertically opposite angles]

∴ ∠MGK = 85° … [From (III)]

Consider ∠e as shown in the figure.

(i)

110o + ∠a = 180° … [Angles in a linear pair]

∴ ∠a = 180° - 110°

∴ ∠a = 70°

(ii)

Line p || line q, and line l is their transversal.

∴ ∠e + 110° = 180° … [Interior angles]

∴ ∠e = 180° - 110°

∴ ∠e = 70°

But, ∠b = ∠e … [Vertically opposite angles]

∴ ∠b = 70°

(iii)

Line p || line q, and line m is their transversal.

∴ ∠c = 115° … [Corresponding angles]

(iv)

115° + ∠d = 180° … [Angles in a linear pair]

∴ ∠d = 180° - 115°

∴ ∠d = 65°

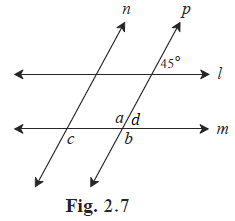
Consider ∠d as shown in the figure.

(i)

Line l || line m, and line p is their transversal.

∴ ∠d = 45° … [Corresponding angles]

Now, ∠d + ∠b = 180° … [Angles in a linear pair]

∴ 45° +∠b = 180°

∴ ∠b = 180° - 45°

∴ ∠b = 135° … (I)

(ii)

∠a = ∠b … [Vertically opposite angles]

∴ ∠a = 135° … [From (I)]

(iii)

Line n || line p, and line m is their transversal.

∴ ∠c = ∠b … [Corresponding angles]

∴ ∠c = 135° … [From (I)]

Given: Ray YZ || ray QR and ray YX || ray QP

To prove: ∠PQR ≅ ∠XYZ

Construction: Extend ray YZ in the opposite direction. It intersects ray QP at point S.

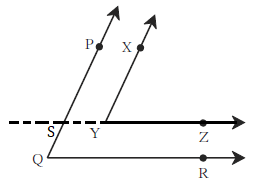
Proof:

Ray YX || ray QP … [Given]

Ray YX || ray SP and seg SY is their transversal [P-S-Q]

∴ ∠XYZ ≅ ∠PSY … (i) [Corresponding angles]

ray YZ || ray QR … [Given]

ray SZ || ray QR and seg PQ is their transversal [S-Y-Z]

∴ ∠PSY ≅ ∠SQR … [Corresponding angles]

∴ ∠PSY ≅ ∠PQR … (II) [P-S-Q]

∴ ∠PQR ≅ ∠XYZ … [From (I) and (II)]

(i)

∠BRT = 105° … (I)

∠ART + ∠BRT = 180° … [Angles in a linear pair]

∴ ∠ART + 105° = 180°

∴ ∠ART = 180° - 105°

∴ ∠ART = 75° … (II)

(ii)

Line AB || line CD and line PQ is their transversal.

∴ ∠CTQ = ∠ART … [Corresponding angles]

∴ ∠CTQ = 75° … [From (II)]

(iii)

Line AB || line CD and line PQ is their transversal.

∴ ∠DTQ = ∠BRT … [Corresponding angles]

∴ ∠DTQ = 105° … [From (I)]

(iv)

∠PRB = ∠ART … [Vertically opposite angles]

∴ ∠PRB = 75° … [From (II)]

Given: y = 108°, x = 71°

Now, x + y = 71° + 108° = 179°

∴ x + y ≠ 180°

∴ The angles x and y are not supplementary.

∴ The angles do not satisfy the interior angles test for parallel lines.

∴ line m and line n are not parallel lines.

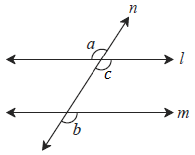
Consider ∠b as shown in the figure.

Given: ∠a ≅ ∠b

To prove: line l| line m

Proof:

Now, ∠a ≅ ∠c … (I) [Vertically opposite angles]

But, ∠a ≅ ∠b … (II) [Given]

∴ ∠b ≅ ∠c … [From (I) and (II)]

But, ∠b and ∠c are corresponding angles on lines l and m when line n is the transversal.

∴ line l || line m … [Corresponding angles test]

Given: ∠a ≅ ∠b and ∠x ≅ ∠y

To prove: line l | line n

Proof:

∠a = ∠b … [Given]

But, ∠a and ∠b are corresponding angles on lines l and m when line K is the transversal.

∴ line l || line m … (I) [Corresponding angles test]

Also, ∠x ≅ ∠y … [Given]

But, ∠x and ∠y are alternate angles on lines m and n when seg PQ is the transversal.

∴ line m || line n … (II) [Alternate angles test]

∴ From (I) and (II),

line l || line m || line n

i.e., line l || line n

Draw a line FG passing through point C and parallel to line AB

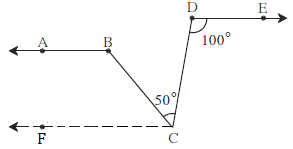
Line FC || ray BA … (I) [Construction]

Ray BA || ray DE … (II) [Given]

Line FC || ray BA || ray DE … (III) [From (I) and (II)]

∴ Line FC || ray DE and seg DC is their transversal

∴ ∠ DCF = ∠ EDC … [Alternate angles]

∴ ∠ DCF = 100° … [∵ ∠D = 100°]

Now, ∠ DCF = ∠ BCF + ∠ BCD … [Angle addition property]

∴ 100° = ∠BCF + 50°

∴ 100° - 50° = ∠BCF

∴ ∠BCF = 50° … (IV)

Now, line FC || ray BA and seg BC is their transversal.

∴ ∠ABC + ∠BCF = 180° … [Interior angles]

∴ ∠ABC + 50° = 180° … [From (IV)]

∴ ∠ABC = 180° - 50°

∴ ∠ABC = 130°

Given: Ray AE || ray BD, and ray AF and ray BC are the bisectors of ∠EAB and ∠ABD respectively.

To prove: line AF || line BC

Proof:

Ray AE || ray BD and seg AB is their transversal.

∴ ∠EAB = ∠ABD … (I) [Alternate angles]

∠FAB = ½ ∠EAB … [Ray AF bisects ∠EAB]

∴ 2∠FAB = ∠EAB … (II)

∠CBA = ½ ∠ABD … [Ray BC bisects ∠ABD]

∴ 2∠CBA = ∠ABD … (III)

∴ 2∠FAB = 2∠CBA [From (I), (II) and (III)]

∴ ∠FAB = ∠CBA

But, ∠FAB and ∠ABC are alternate angles on lines AF and BC when seg AB is the transversal.

∴ line AF || line BC … [Alternate angles test]

Given: Ray PR || ray QS and Ray PR and ray QS are the bisectors of ∠BPQ and ∠PQC respectively.

To prove: line AB || line CD

Proof:

Ray PR || ray QS and seg PQ is their transversal.

∠RPQ = ∠SQP … (I) [Alternate angles]

∠RPQ = ½ ∠BPQ … (II) [Ray PR bisects ∠BPQ]

∠SQP = ½ ∠PQC … [Ray QS bisects ∠PQC]

∴ ½ ∠BPQ = ½ ∠PQC

∴ ∠BPQ = ∠PQC

But, ∠BPQ and ∠PQC are alternate angles on lines AB and CD when line EF is the transversal.

∴ line AB || line CD … [Alternate angles test]

(C)

If a transversal intersects two parallel lines then the sum of interior angles on the same side of the transversal is 180o.

(C)

The number of angles formed by a transversal of two lines is 8.

(A)

A transversal intersects two parallel lines. If the measure of one of the angles is 40° then the measure of its corresponding angle is 40o.

(B)

In ∆ ABC, ∠A + ∠B + ∠C = 180°

∴ ∠C = 180° - ∠A - ∠B = 180° - 76° - 48° = 56°

∴ ∠C = 56°

(A)

Two parallel lines are intersected by a transversal. If measure of one of the alternate interior angles is 75° then the measure of the other angle is 105°.

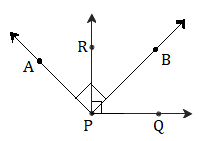
(i)

Complementary angles:

∠RPQ = 90° … [Ray PQ ⊥ ray PR]

∴ ∠RPB + ∠BPQ = 90° … [Angle addition property]

∴ ∠RPB and ∠BPQ are pair of complementary angles.

Also, ∠APB = 90° … [Ray PA ⊥ ray PB]

∴ ∠APR + ∠RPB = 90°

∴ ∠APR and ∠RPB are pair of complementary angles.

(ii)

Supplementary angles:

∠APB + ∠RPQ = 90° + 90° = 180°

∴ ∠APB and ∠RPQ are pair of supplementary angles.

(iii)

Congruent angles:

∠APB = ∠RPQ … [Each of 90°]

∴ ∠APR + ∠RPB = ∠RPB + ∠BPQ … [Angle addition property]

∴ ∠APR = ∠BPQ

∴ ∠APR ≅ ∠BPQ

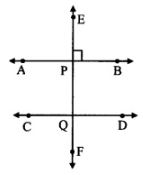
Given:

Line AB || line CD and line EF intersects them at P and Q respectively.

Line EF ⊥ line AB

To prove: line EF ⊥ line CD

Proof:

Line EF ⊥ line AB … [Given]

∴ ∠EPB = 90° … (I)

Line AB || line CD and line EF is their transversal.

∴ ∠EPB ≅ ∠PQD … (II) [Corresponding angles]

∴ ∠PQD = 90° … [From (I) and (II)]

∴ line EF ⊥ line CD

∠x = 130° … [Vertically opposite angles]

∠y = 50° … [Vertically opposite angles]

Here, m∠ABC + m∠BCD = 130° + 50° = 180°

But, ∠ABC and ∠BCD are a pair of interior angles on lines l and m when line n is the transversal.

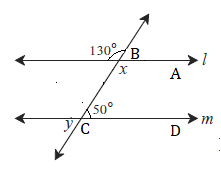
∴ line l || line m … [Interior angles test]

Given: y : z = 3 : 7

Let the common multiple be k

∴ ∠y = 3k and ∠z = 7k … (I)

Line AB || line EF and line PQ is their transversal … [Given]

∴ ∠x = ∠z

∴ ∠x = 7k … (II) [From (I)]

Line AB || line CD and line PQ is their transversal … [Given]

∴ ∠x + ∠y = 180°

∴ 7k + 3k = 180°

∴ 10k = 180°

∴ k = 18°

∴ ∠x = 7k = 7(18°) … [From (II)]

∴ ∠x = 126°

Given: ∠a = 80°

Now, ∠g = ∠a … [Alternate exterior angles]

∴ ∠g = 80° … (I)

Now, line q || line r and line p is their transversal.

∴ ∠f + ∠g = 180° … [Interior angles]

∴ ∠f + 80° = 180° … From (I)

∴ ∠f = 180° - 80°

∴ ∠f = 100°

Given: line AB || line CF and line BC || line ED

To prove: ∠ABC = ∠FDE

Proof:

Line AB || line PF and line BC is their transversal.

∴ ∠ABC = ∠BCD … (I) [Alternate angles]

Line BC || line ED and line CD is their transversal.

∴ ∠BCD = ∠FDE … (II) [Corresponding angles]

∴ ∠ABC = ∠FDE … [From (I) and (II)]

Given: line AB || line CD

Rays QX, RX, QY, RY are the bisectors of ∠AQR, ∠QRC, ∠BQR and ∠QRD respectively.

To prove: □QXRY is a rectangle.

Proof:

∠XQA = ∠XQR = x° … (I) [Ray QX bisects ∠AQR]

∠YQR = ∠YQB = y° … (II) [Ray QY bisects ∠BQR]

∠XRQ = ∠XRC = u° … (III) [Ray RX bisects ∠CRQ]

∠YRQ = ∠YRD = v° …(IV) [Ray RY bisects ∠DRQ]

Since, line AB || line CD and line PS is their transversal.

∴ ∠AQR+ ∠CRQ = 180° … [Interior angles]

∴ (∠XQA + ∠XQR) + (∠XRQ + ∠XRC) = 180° … [Angle addition property]

∴ (x + x) + (u + u) = 180° … [From (I) and (II)]

∴ 2x + 2u = 180°

∴ 2(x + u) = 180°

∴ x + u = 90° … (V)

In ∆XQR,

∠XQR + ∠XRQ + ∠QXR = 180° … [Sum of the measures of the angles of triangle is 180°]

∴ x + u + ∠QXR = 180° … [From (I) and (III)]

∴ 90 + ∠QXR = 180° … [From (V)]

∴ ∠QXR = 180° - 90°

∴ ∠QXR = 90° … (VI)

Similarly, we can prove that,

∴ y + v = 90°

i.e. ∠QYR = 90° … (VII)

Now, ∠AQR + ∠BQR = 180° … [Angles is linear pair]

∴ (∠XQA + ∠XQR) + (∠YQR + ∠YQB) = 180° … [Angle addition property]

∴ (x + x) + (y + y) = 180° … [From (I) and (II)]

∴ 2x + 2y = 180°

∴ 2(x + y) = 180°

∴ x + y = 90°

i.e. ∠XQR + ∠YQR = 90° … [From (I) and (II)]

∴ ∠XQY = 90° … (VIII) [Angle addition property]

Similarly, we can prove that,

∠XRY = 90° … (IX)

In □QXRY,

∠QXR = ∠QYR = ∠XQY = ∠XRY = 90° … [From (vi), (vii), (viii) and (ix)]

∴ □QXRY is a rectangle.