Class 9 MAHARASHTRA STATE TEXTBOOK BUREAU Solutions Maths Chapter 4 - Constructions of Triangles
Constructions of Triangles Exercise 4.1
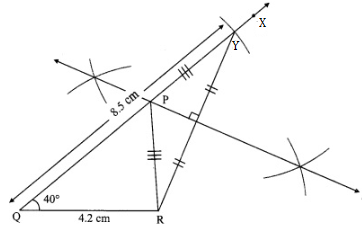
Solution 1
Steps of construction:
(1) Draw seg QR of length 4.2 cm.
(2) Draw ray QX such that m ∠XQR = 40°.
(3) Mark point Y on ray QX such that d(Q, Y) = 8.5 cm
(4) Draw seg YR.
(5) Construct the perpendicular bisector of seg YR.
(6) Name the point of intersection of ray QX and the perpendicular bisector of YR as P.
(7) Draw seg PR.
∆PQR is the required triangle.
Solution 2
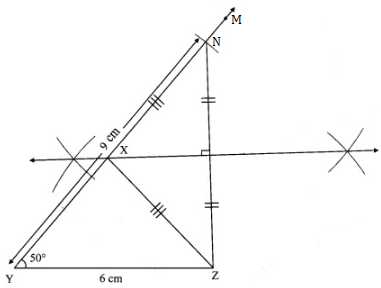
Steps of construction:
(1) Draw seg YZ of length 6 cm.
(2) Draw ray YM such that m ∠MYZ = 50°.
(3) Mark point N on ray YM such that d(Y, N) = 9 cm
(4) Draw seg ZN.
(5) Construct the perpendicular bisector of seg ZN.
(6) Name the point of intersection of ray YM and the perpendicular bisector of ZN as X.
(7) Draw seg XZ.
∆XYZ is the required triangle.
Solution 3
Steps of construction:
(1) Draw seg CB of length 6.2 cm.
(2) Draw ray CX such that m ∠XCB = 50°.
(3) Mark point Y on ray XC such that d(C, Y) = 9.8 cm
(4) Draw seg YB.
(5) Construct the perpendicular bisector of seg YB.
(6) Name the point of intersection of ray CX and the perpendicular bisector of YB as A.
(7) Draw seg AB.
∆ABC is the required triangle.

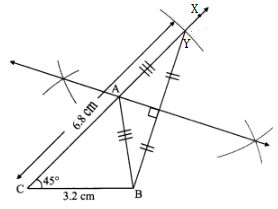
Solution 4
Perimeter of ΔABC = AB + BC + CA
∴ AB + BC + CA = 10 cm
∴ AB + 3.2 cm + CA = 10 cm … (Since, BC = 3.2 cm)
∴ AB + CA = 6.8 cm … (I)
Steps of construction:
(1) Draw seg CB of length 3.2 cm.
(2) Draw ray CX such that m ∠XCB = 45°.
(3) Mark point Y on ray XC such that d(C, Y) = 6.8 cm
(4) Draw seg YB.
(5) Construct the perpendicular bisector of seg YB.
(6) Name the point of intersection of ray CX and the perpendicular bisector of YB as A.
(7) Draw seg AB.
∆ABC is the required triangle.
Constructions of Triangles Exercise 4.2
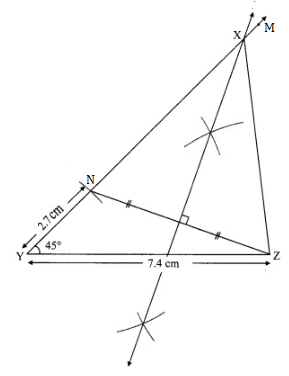
Solution 1
Steps of construction:
(1) Draw YZ of length 7.4 cm.
(2) Draw ray YM such that ∠MYZ = 45°
(3) Mark point N on ray YM such that l(YN) = 2.7 cm.
(4) Construct the perpendicular bisector of seg NZ.
(6) Mark the point of intersection of perpendicular bisector of seg NZ and ray YM as X.
(7) Draw seg XZ.
∆XYZ is the required triangle.
Solution 2
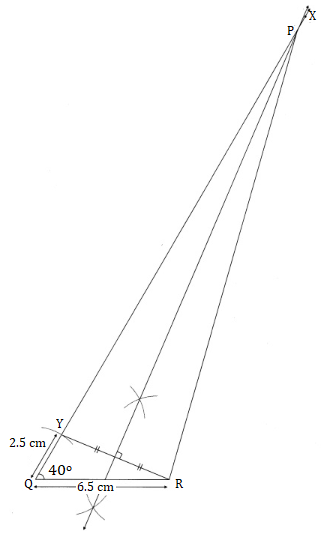
Steps of construction:
(1) Draw QR of length 6.5 cm.
(2) Draw ray QX such that ∠XQR = 40°
(3) Mark point Y on ray YR such that l(QY) = 2.5 cm.
(4) Construct the perpendicular bisector of seg YR.
(6) Mark the point of intersection of perpendicular bisector of seg YR and ray QX as P.
(7) Draw seg PR.
∆PQR is the required triangle.
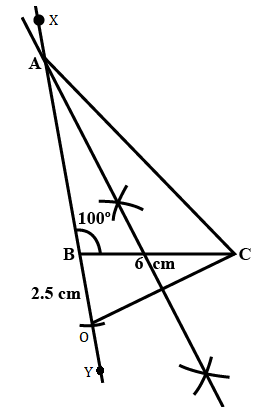
Solution 3
Steps of construction:
(1) Draw BC of length 6 cm.
(2) Draw ray BX such that ∠XBC = 100°
(3) Take point O on the opposite ray BY of ray BX such that BO = 2.5 cm.
(4) Construct perpendicular bisector of seg CO.
(5) Name the point of intersection of ray BX and the perpendicular bisector of CO as A.
(6) Draw seg AC.
∆ABC is the required triangle.
Constructions of Triangles Exercise 4.3
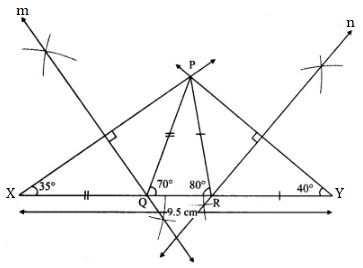
Solution 1
Steps of construction:
(1) Draw seg XY of length 9.5 cm.
(2) Draw a ray making angle of 35° at point X.
(3) Draw another ray making an angle of 40° at point Y.
(4) Name the point of intersection of the two rays as P.
(5) Draw the perpendicular bisectors of seg PX and seg PY. Name the points as
Q and R respectively where the perpendicular bisectors intersect line XY.
(6) Draw seg PQ and seg PR.
∆PQR is the required triangle.
Solution 2
Steps of construction:
(1) Draw seg AB of length 10.5 cm.
(2) Draw a ray making angle of 29° at point B.
(3) Draw another ray making an angle of 23° at point A.
(4) Name the point of intersection of the two rays as Z.
(5) Draw the perpendicular bisectors of seg ZA and seg ZB. Name the points as
X and Y respectively where the perpendicular bisectors intersect line AB.
(6) Draw seg ZX and seg ZY.
∆XYZ is the required triangle.

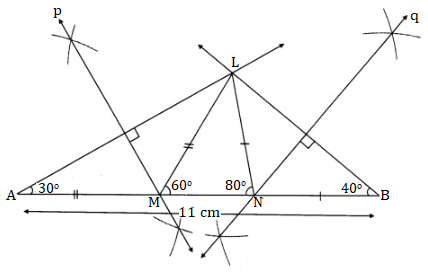
Solution 3
Steps of construction:
(1) Draw seg AB of length 10.5 cm.
(2) Draw a ray making angle of 30° at point A.
(3) Draw another ray making an angle of 40° at point B.
(4) Name the point of intersection of the two rays as L.
(5) Draw the perpendicular bisectors of seg LA and seg LB. Name the points as
M and N respectively where the perpendicular bisectors intersect line AB.
(6) Draw seg LM and seg LN.
∆LMN is the required triangle.
Constructions of Triangles Exercise Problem set 4
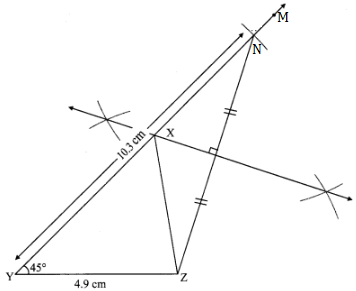
Solution 1
Steps of construction:
(1) Draw seg YZ of length 4.9 cm.
(2) Draw ray YM such that m ∠MYZ = 45°.
(3) Mark point N on ray MY such that d(Y, N) = 10.3 cm
(4) Draw seg NZ.
(5) Construct the perpendicular bisector of seg NZ.
(6) Name the point of intersection of ray MY and the perpendicular bisector of NZ as X.
(7) Draw seg XZ.
∆XYZ is the required triangle.
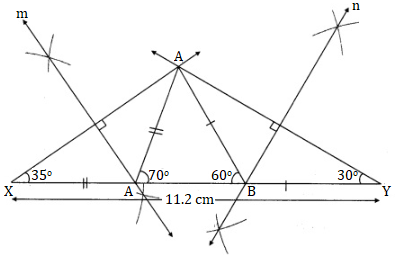
Solution 2
Steps of construction:
(1) Draw seg XY of length 11.2 cm.
(2) Draw a ray making angle of 35° at point X.
(3) Draw another ray making an angle of 30° at point Y.
(4) Name the point of intersection of the two rays as A.
(5) Draw the perpendicular bisectors of seg AX and seg AY. Name the points as
B and C respectively where the perpendicular bisectors intersect line XY.
(6) Draw seg AB and seg AC.
∆ABC is the required triangle.
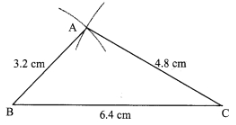
Solution 3
The ratio of lengths of the sides of a triangle is 2:3:4
Let the common multiple be x
∴ In ∆ABC,
AB = 2x cm, AC = 3x cm, BC = 4x cm
Now, Perimeter of triangle = 14.4 cm
∴ AB + BC + AC= 14.4
∴ 9x = 14.4
∴ x = 1.6
∴ AB = 2x = 2 × 1.6 = 3.2 cm
∴ AC = 3x = 3 × 1.6 = 4.8 cm
∴ BC = 4x = 4 × 1.6 = 6.4 cm
Steps of construction:
(1) Draw seg BC of length 6.4 cm.
(2) Draw an arc of length 3.2 cm from B.
(3) Draw an arc of length 4.8 cm from C.
(4) Let the arcs intersect at point A.
(5) Join AB and AC.
∆ABC is the required triangle.
Solution 4
Steps of construction:
(1) Draw QR of length 6.4 cm.
(2) Draw ray QX such that ∠XQR = 55°
(3) Mark point Y on ray YR such that l(QY) = 2.4 cm.
(4) Construct the perpendicular bisector of seg YR.
(6) Mark the point of intersection of perpendicular bisector of seg YR and ray QX as P.
(7) Draw seg PR.
∆PQR is the required triangle.


